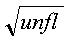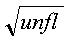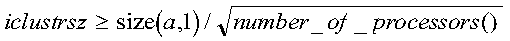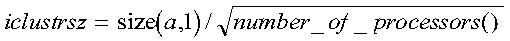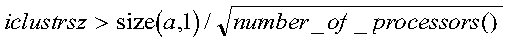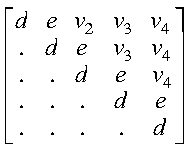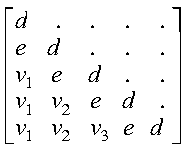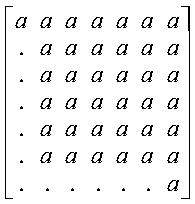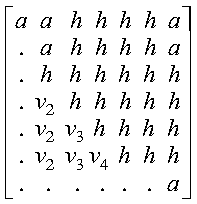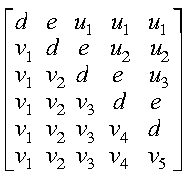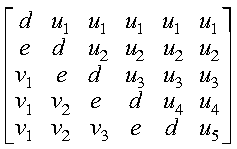Guide and Reference

Eigensystem Analysis and Singular Value Analysis (HPF)

This chapter describes the eigensystem analysis and singular value analysis subroutines that can be called from an HPF program.

Overview of the Eigensystem Analysis and Singular Value Analysis Subroutines

The eigensystem analysis and singular value analysis subroutines include a subset of the ScaLAPACK subroutines.

Note:

These subroutines are designed to be consistent with the proposals for the Fortran 90 BLAS and the Fortran 90 LAPACK. (See references [30] and [31].) If these subroutines do not comply with any eventual proposal for HPF interfaces to the PBLAS and ScaLAPACK, IBM will consider updating them to do so. If IBM updates these subroutines, the update could require modifications of the calling application program.

Table 134. List of Eigensystem Analysis and Singular Value Analysis Subroutines (HPF)

Descriptive Name	Long-Precision Subroutine	Page
Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix	SYEVX	SYEVX--Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix
Reduce a Real Symmetric Matrix to Tridiagonal Form	SYTRD	SYTRD--Reduce a Real Symmetric Matrix to Tridiagonal Form
Reduce a General Matrix to Upper Hessenberg Form	GEHRD	GEHRD--Reduce a General Matrix to Upper Hessenberg Form
Reduce a General Matrix to Bidiagonal Form	GEBRD	GEBRD--Reduce a General Matrix to Bidiagonal Form

Eigensystem Analysis and Singular Value Analysis Subroutines

This section contains the eigensystem analysis subroutine descriptions.

SYEVX--Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix

This subroutine computes selected eigenvalues and, optionally, the eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying a range of values or a range of indices for the eigenvalues.

The eigenvalue computation performed by this subroutine depends on which of the vl, vu, il, and iu arguments you specify:

Case 1:

If vl, vu, il, iu are all not present, all eigenvalues are found.

Case 2:

If vl and vu are present and il and iu not present, then all eigenvalues in the interval [vl,vu] are found.

Case 3:

If il or iu, or both, are present and vl and vu are not present, then the il-th through iu-th eigenvalues are found.

Any other combination of vl, vu, il, iu being present or not present is considered an input-argument error.

If the assumed-shape arrays for A and w have a size of zero, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13], [21], [31], [41], [24], [25], and [26].

Table 135. Data Types

A, vl, vu, abstol, orfac, Z, w, gap	ifail, iclustr	Subroutine
Long-precision real	Integer	SYEVX

Syntax

On Entry

a

is the symmetric matrix A, where:

If uplo = 'U', the array contains the upper triangle of the symmetric matrix A in its upper triangle, and its strictly lower triangular part is not referenced.

If uplo = 'L', the array contains the lower triangle of the symmetric matrix A in its lower triangle, and its strictly upper triangular part is not referenced.

Type: required

Specified as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 135, where size(a,1) = size(a,2).

w

See 'On Return'.

uplo

indicates whether the upper or lower triangular part of the symmetric matrix A is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Type: required

Specified as: a single character; uplo = 'U' or 'L'.

vl

has the following meaning:

If vl and vu are present and il and iu are not present, then vl is the lower bound of the interval to be searched for eigenvalues.

Type: optional

Default: none

Specified as: a number of the data type indicated in Table 135; vl < vu.

vu

has the following meaning:

If vl and vu are present and il and iu are not present, then vu is the upper bound of the interval to be searched for eigenvalues.

Type: optional

Default: none

Specified as: a number of the data type indicated in Table 135; vl < vu.

il

has the following meaning:

If il is present and vl and vu are not present, then il is the index (from smallest to largest) of the smallest eigenvalue to be returned.

Type: optional

Default: il = 1

Specified as: a fullword integer; il >= 1.

iu

has the following meaning:

If iu is present and vl and vu are not present, then iu is the index (from smallest to largest) of the largest eigenvalue to be returned.

Type: optional

Default: iu = size(a,1)

Specified as: a fullword integer; min(il, size(a,1)) <= iu <= size(a,1).

abstol

is the absolute tolerance for the eigenvalues. An approximate eigenvalue is accepted as converged when it is determined to lie in an interval [a,b] of width less than or equal to:

abstol+epsilon(max(|a|, |b|))

where epsilon is the machine precision. If abstol is less than or equal to zero, then epsilon(norm(T)) is used in its place, where norm(T) is the 1-norm of the tridiagonal matrix obtained by reducing A to tridiagonal form. For most problems, this is the appropriate level of accuracy to request.

For certain strongly graded matrices, greater accuracy can be obtained in very small eigenvalues by setting abstol to a very small positive number. However, if abstol is less than:

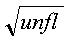
where unfl is the underflow threshold, then:

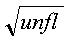
is used in its place.

Eigenvalues are computed most accurately when abstol is set to twice the underflow threshold--that is, (2)(unfl).

If z is present, then setting abstol to unfl, the underflow threshold, yields the most orthogonal eigenvectors.

Type: optional

Default: abstol = epsilon(norm(T))

Specified as: a number of the data type indicated in Table 135.

m

See 'On Return'.

nz

See 'On Return'.

orfac

specifies which eigenvectors should be reorthogonalized. Eigenvectors that correspond to eigenvalues which are within:

ortol = (orfac)(norm(A))

of each other (where norm(A) is the 1-norm of A) are to be reorthogonalized.

However, if the workspace is insufficient (see iclustrsz), ortol may be decreased until all eigenvectors to be reorthogonalized can be stored in one process.

If orfac is zero, no reorthogonalization is done.

If orfac is less than zero, a default value of 10^-3 is used.

Type: optional

Default: orfac = 10^-3

Specified as: a number of the data type indicated in Table 135.

z

See 'On Return'.

ifail

See 'On Return'.

iclustr

See 'On Return'.

gap

See 'On Return'.

iclustrsz

is the variable used to calculate how much additional workspace to use for the eigenvector computation.

The computed eigenvectors may not be orthogonal if the minimum workspace is used and ortol is too small; therefore, if you want to guarantee orthogonality (at the cost of potentially compromising performance), set iclustrsz, then the following additional workspace is used to compute the eigenvectors:

(iclustrsz-1)(size(a,1))

where iclustrsz is the number of eigenvalues in the largest cluster, where a cluster is defined as a set of close eigenvalues:

{w_k, ..., w_{k+iclustrsz-1} | w_j+1 <= w_j+orfac(2)(norm(A))}

If the workspace is too small to guarantee orthogonality, this subroutine attempts to maintain orthogonality in the clusters with the smallest spacing between the eigenvalues.

Relationship between workspace, orthogonality, and performance:

• If iclustrsz is:

  
  
  
  
  

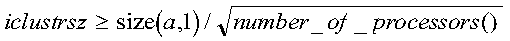
  then providing enough space to compute all the eigenvectors orthogonally causes serious degradation in performance. In the limit (iclustrsz = size(a,1)-1), performance may be no better than using one process.

• If iclustrsz is:

  
  
  
  
  

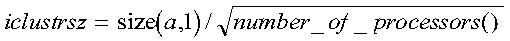
  then reorthogonalizing all eigenvectors increases the total execution time by a factor of 2 or more.

• If iclustrsz is:

  
  
  
  
  

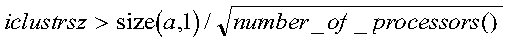
  then execution time grows as the square of the cluster size, assuming all other factors remain equal and there is enough workspace. Less workspace means less reorthogonalization, but faster execution.

Type: optional

Default: iclustrsz = 1

Specified as: a fullword integer; iclustrsz > 0.

info

See 'On Return'.

On Return

a

is the symmetric matrix A, where:

If uplo = 'U', the upper triangle and diagonal of the symmetric matrix A are overwritten; that is, the original input is not preserved.

If uplo = 'L', the lower triangle and diagonal of the symmetric matrix A are overwritten; that is, the original input is not preserved.

Type: required

Returned as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 135.

w

On normal exit (see info), it is the vector w, containing the selected eigenvalues in ascending order in the first m elements of w.

A copy of w is aligned with every element of A:

   !HPF$ ALIGN W(*) WITH A(*,*)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 135, where size(w) = size(a,1).

m

is the number of eigenvalues found.

Type: optional

Returned as: a fullword integer; 0 <= m <= size(a,1).

nz

has the following meaning:

If z is not present, then nz is ignored.

If z is present, then nz is the number of eigenvectors computed--that is, the number of columns of Z used in the computation. On output, nz = m, unless there is insufficient space and this subroutine is not able to detect it before starting the computation.

Note:

This subroutine is able to detect insufficient space without computation, unless vl and vu are present and eigenvalues are being selected by specifying a range of values.

To get all the eigenvectors requested, you must supply sufficient space to hold the eigenvectors in Z and sufficient workspace to compute them must be available.

Type: optional

Returned as: a fullword integer; 0 <= nz <= m.

z

is the general matrix Z. On normal exit (see info), the first m columns of the matrix Z contain the orthonormal eigenvectors of the symmetric matrix A, corresponding to the selected eigenvalues. If an eigenvector fails to converge, then that column of the general matrix Z contains the last approximation to the eigenvector, and the index of the eigenvector is returned in ifail, if ifail is present.

Type: optional

Returned as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 135, where size(z,1) = size(a,1) and size(z,2) = size(a,2).

ifail

has the following meaning:

If z is not present, then ifail is ignored.

If z is present, it is vector ifail, where:

• If there is a normal exit (see info), the first m elements of ifail are zero.

• If there is an error exit (where one or more eigenvectors failed to converge--see info), ifail contains the indices of the eigenvectors that failed to converge.

A copy of ifail is aligned with every element of A:

   !HPF$ ALIGN IFAIL(*) WITH A(*,*)

Type: optional

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 135; 0 <= ifail_i <= size(a,1), where size(ifail) = size(a,1).

iclustr

has the following meaning:

If z is not present, then iclustr is ignored.

If z is present, it is vector iclustr, containing the indices of the eigenvectors corresponding to a cluster of eigenvalues that could not be reorthogonalized due to insufficient workspace. Eigenvectors corresponding to clusters of eigenvalues indexed iclustr_2i-1 to iclustr_2i could not be reorthogonalized due to lack of workspace. Hence, the eigenvectors corresponding to these clusters may not be orthogonal.

iclustr is a zero-terminated vector; that is, the last element of iclustr is set to zero. Assuming that k is the number of clusters, then:

iclustr_2k <> 0 and iclustr_2k+1 = 0

A copy of iclustr is aligned with every element of A:

   !HPF$ ALIGN ICLUSTR(*) WITH A(*,*)

Type: optional

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 135; 0 <= iclustr_i <= size(a,1), where size(iclustr) = (2)(number_of_processors()).

gap

has the following meaning:

If z is not present, then gap is ignored.

If z is present, it is vector gap, containing the gap between the eigenvalues whose eigenvectors could not be reorthogonalized. The values in this vector correspond to the clusters indicated by iclustr. As a result, the dot product between the eigenvectors corresponding to the i-th cluster may be as high as ((C)(size(a,1)))/gap_i, where C is a small constant.

A copy of gap is aligned with every element of A:

   !HPF$ ALIGN GAP(*) WITH A(*,*)

Type: optional

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 135, where size(gap) = (number_of_processors()).

info

has the following meaning, when info is present:

If info = 0, then no input-argument errors or computational errors occurred. This indicates a normal exit.

Note:

One use of info in ScaLAPACK is to identify whether input-argument errors occurred. Because Parallel ESSL terminates the application if input-argument errors occur, the setting of info is irrelevant for these errors.

If info > 0, then one or more of the following computational errors occurred and the appropriate error messages were issued, indicating an error exit, where:

• If mod(info, 2) <> 0, then one or more eigenvectors failed to converge. Their indices are stored in ifail, if ifail is present. (Ensure that abstol = (2)(unfl).)

• If mod(info/2, 2) <> 0, then the eigenvectors corresponding to one or more clusters of eigenvalues could not be reorthogonalized because of insufficient workspace. The indices of the clusters are stored in iclustr, if iclustr is present.

• If mod(info/4, 2) <> 0, then all the eigenvectors between vl and vu could not be computed because of insufficient space. The number of eigenvectors computed is returned in nz, if nz is present.

• If mod(info/8, 2) <> 0, then one of more eigenvalues were not computed. (Ensure that abstol = (2)(unfl).)

When info is not present and a computational error occurs, the information for the computational error is issued in an error message, and your program is terminated.

Type: optional

Returned as: a fullword integer; info >= 0.

Notes and Coding Rules

1. The assumed-shape arrays must have the exact size required for the computation, that is:
   • size(a,1) = size(a,2) = size(w)
   • If z is present:
     • size(z,1) = size(a,1)
     • size(z,2) = size(a,2)
   • If ifail and z are present, size(ifail) = size(a,1)
   • If iclustr and z are present, size(iclustr) = (2)(number_of_processors())
   • If gap and z are present, size(gap) = (number_of_processors())

2. This subroutine accepts lowercase letters for the uplo argument.

3. The assumed-shape arrays must have no common elements; otherwise, results are unpredictable.

4. Eigenvectors associated with tightly clustered eigenvalues may not be orthogonal.

5. Eigenvectors that are on different processes are not reorthogonalized. For details, see the argument description for iclustrsz.

6. For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"

7. Block-cyclic data distribution is required for your array data. Because data directives are included in the interface module PESSL_HPF, you can specify any data distribution for your vectors and matrices, and the XL HPF compiler will, if necessary, redistribute the data prior to calling this subroutine. For how to code your HPF directives, see "Distributing Data in an HPF Program". For a sample program including directives, see Figure 9.

8. The restrictions given in "Notes and Coding Rules" also apply to this subroutine.

9. An example of the use of this subroutine in a thermal diffusion application program is shown in Appendix B. "Sample Programs". See "Program Main (HPF)".

Function

This subroutine computes selected eigenvalues and, optionally, the eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying a range of values or a range of indices for the eigenvalues. The computation involves the following steps:

1. Reduce the real symmetric matrix A to real symmetric tridiagonal form.

2. Compute the requested eigenvalues of the real symmetric tridiagonal matrix using bisection.

3. If requested, compute the eigenvectors of the real symmetric tridiagonal matrix using inverse iteration, and then back transform the eigenvectors to obtain the eigenvectors of the real symmetric matrix A.

Error Conditions

HPF-specific errors are listed below. All errors listed in "Error Conditions" also apply to this subroutine; however, for computational errors, if you do not specify the optional info argument, your program terminates as a result of the computational error.

Note:

If a computational error occurs, information is stored in ifail, iclustr, and nz only if these arguments are present.

Input-Argument Errors

Stage 1

1. It is not possible to determine the type of eigenvalue computation to perform--that is, one of the following valid combinations of vl, vu, il, and iu did not occur:

   • vl, vu, il, iu are all not present (all eigenvalues are found).

   • vl and vu are present and il and iu not present (all eigenvalues in the interval [vl,vu] are found).

   • il or iu, or both, are present and vl and vu are not present (the il-th through iu-th eigenvalues are found).

2. iclustrsz is present and iclustrsz < 1.

Stage 2

1. The rank of the ultimate align target is greater than 2 for a.
2. The process rank is not 1 or 2 for a.
3. z is present and:
   1. The rank of the ultimate align target is greater than 2 for z.
   2. The process rank is not 1 or 2 for z.
   3. The process rank is not the same for a and z.

Stage 3

z is present, and the process grid is not the same for a and z.

Stage 4

1. z is present, and the data distribution is inconsistent for a and z.
2. z is not present, and the data distribution is unsupported for a.

Stage 5

w is not replicated and collapsed.

Stage 6

1. z is present, and the shape of the assumed-shape arrays a, z, and w is incompatible:
   1. size(a,1) <> size(a,2) or
   2. size(a,1) <> size(w) or
   3. size(a,1) <> size(z,1) or
   4. size(z,2) <> size(a,2)
2. z is not present, and the shape of the assumed-shape arrays a and w is incompatible:
   1. size(a,1) <> size(a,2) or
   2. size(a,1) <> size(w)
3. The shape of the assumed-shape array for a is invalid: size(a,1) <> size(a,2)

Stage 7

z and the optional arrays, indicated below, are present, and:

1. ifail is not replicated and collapsed.
2. The shape of the assumed-shape arrays for a and ifail is incompatible: size(a,1) <> size(ifail).
3. iclustr is not replicated and collapsed.
4. The shape of the assumed-shape array for iclustr is invalid: size(iclustr,1) <> (2)(number_of_processors()).
5. gap is not replicated and collapsed.
6. The shape of the assumed-shape array for gap is invalid: size(gap,1) <> (number_of_processors()).

Stage 8

1. The data distribution for a is unsupported.
2. z is present, and the data distribution for z is unsupported.

Example

This example shows how to find all the eigenvalues and eigenvectors of a real symmetric matrix A of order 4. As in "Example", array data for A and Z is block-cyclically distributed using a 2 × 2 process grid, with a copy of vectors w, ifail, iclustr, and gap each being aligned with every element of A.

!HPF$ PROCESSORS PROC(2,2)
!HPF$ ALIGN W(*) WITH A(*,*)
!HPF$ DISTRIBUTE (CYCLIC, CYCLIC) ONTO PROC :: A, Z
 
CALL SYEVX( A , W , 'U' , Z=Z )
 
      -or-
 
!HPF$ PROCESSORS PROC(2,2)
!HPF$ ALIGN W(*) WITH A(*,*)
!HPF$ ALIGN IFAIL(*) WITH A(*,*)
!HPF$ ALIGN ICLUSTR(*) WITH A(*,*)
!HPF$ ALIGN GAP(*) WITH A(*,*)
!HPF$ DISTRIBUTE (CYCLIC, CYCLIC) ONTO PROC :: A, Z
 
 CALL SYEVX( A, W, 'U', ABSTOL=-1.0D0, M=M, NZ=NZ, ORFAC=-1.0D0, Z=Z,
           IFAIL=IFAIL, ICLUSTR=ICLUSTR, GAP=GAP, ICLUSTRSZ=1, INFO=INFO)

Input

Symmetric matrix A of order 4:

 *                    *
 | 5.0  4.0  1.0  1.0 |
 |  .   5.0  1.0  1.0 |
 |  .    .   4.0  2.0 |
 |  .    .    .   4.0 |
 *                    *

Output

The upper triangle, including the diagonal, of the symmetric matrix A is overwritten; that is, the original input is not preserved.

m = 4 (if m is present)

nz = 4 (if nz is present)

Vector w of length 4:

w = (1.00, 2.00, 5.00, 10.00)

General matrix Z of order 4:

 *                                    *
 |  0.7071   0.0000  -0.3162  -0.6325 |
 | -0.7071   0.0000  -0.3162  -0.6325 |
 |  0.0000  -0.7071   0.6325  -0.3162 |
 |  0.0000   0.7071   0.6325  -0.3162 |
 *                                    *

Vector ifail of length 4: (if ifail is present)

ifail = (0, 0, 0, 0)

Vector iclustr of length 8 (= (2)(number_of_processors())): (if iclustr is present)

iclustr = (0, 0, 0, 0, 0, 0, 0, 0)

Vector gap of length 4 (= number_of_processors()): (if gap is present)

gap = (-1.0, -1.0, -1.0, -1.0)

info = 0 (if info is present)

SYTRD--Reduce a Real Symmetric Matrix to Tridiagonal Form

This subroutine reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

If the assumed-shape array for A has a size of zero, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13], [21], [31], and [41].

Table 136. Data Types

A, d, e, tau	Subroutine
Long-precision real	SYTRD

Syntax

On Entry

a

is the symmetric matrix A, where:

If uplo = 'U', the array contains the upper triangle of the symmetric matrix A in its upper triangle, and its strictly lower triangular part is not referenced.

If uplo = 'L', the array contains the lower triangle of the symmetric matrix A in its lower triangle, and its strictly upper triangular part is not referenced.

Type: required

Specified as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 136, where size(a,1) = size(a,2).

d

See 'On Return'.

e

See 'On Return'.

tau

See 'On Return'.

uplo

indicates whether the upper or lower triangular part of the symmetric matrix A is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Type: required

Specified as: a single character; uplo = 'U' or 'L'.

info

See 'On Return'.

On Return

a

is the updated symmetric matrix A, containing the results of the computation, where:

If uplo = 'U', the diagonal and first superdiagonal of A are overwritten by the corresponding elements of the tridiagonal matrix T. The elements above the first superdiagonal, with tau, represent the orthogonal matrix Q as a product of elementary reflectors.

If uplo = 'L', the diagonal and first subdiagonal of A are overwritten by the corresponding elements of the tridiagonal matrix T. The elements below the first subdiagonal, with tau, represent the orthogonal matrix Q as a product of elementary reflectors.

See "Function", for more information.

Type: required

Returned as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 136.

d

is the updated vector d, containing the diagonal elements of the tridiagonal matrix T.

The elements of d must be replicated across each element of the corresponding column of A; that is, a copy of d is aligned with every row of A:

   !HPF$ ALIGN D(:) WITH A(*,:)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 136, where size(d) = size(a,1).

e

is the updated vector e, containing the off-diagonal elements of the tridiagonal matrix T, where:

If uplo = 'U', then e₁ = 0 and e_2:size(e) contains the superdiagonal elements of the tridiagonal matrix T.

If uplo = 'L', then e_1:size(e)-1 contains the subdiagonal elements of the tridiagonal matrix T, and e_size(e) = 0.

The elements of e must be replicated across each element of the corresponding column of A; that is, a copy of e is aligned with every row of A:

   !HPF$ ALIGN E(:) WITH A(*,:)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 136, where size(e) = size(a,1).

tau

is the updated vector tau, containing the scalar factors of the elementary reflectors, where:

If uplo = 'U', then tau₁ = 0 and tau_2:size(tau) contains the scalar factors of the elementary reflectors.

If uplo = 'L', then tau_{1:size(tau)-1} contains the scalar factors of the elementary reflectors and tau_size(tau) = 0

The elements of tau must be replicated across each element of the corresponding column of A; that is, a copy of tau is aligned with every row of A:

   !HPF$ ALIGN TAU(:) WITH A(*,:)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 136, where size(tau) = size(a,1).

info

indicates that a successful computation occurred.

Type: optional

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

1. The assumed-shape arrays must have the exact size required for the computation, that is:

   size(a,1) = size(a,2) = size(d) = size(e) = size(tau)

2. This subroutine accepts lowercase letters for the uplo argument.

3. The assumed-shape arrays must have no common elements; otherwise, results are unpredictable.

4. For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"

5. Block-cyclic data distribution is required for your array data. Because data directives are included in the interface module PESSL_HPF, you can specify any data distribution for your vectors and matrix, and the XL HPF compiler will, if necessary, redistribute the data prior to calling this subroutine. For how to code your HPF directives, see "Distributing Data in an HPF Program". For a sample program including directives, see Figure 9.

6. The restrictions given in "Notes and Coding Rules" also apply to this subroutine.

Function

This subroutine reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

where:

• A is a symmetric matrix, where n = size(a,1) = size(a,2)
• Matrix Q represents the following:

  • For uplo = 'U', the matrix Q is the product of elementary reflectors: Q = H_n-1 ... H₂ H₁,

    where:

    For each i: H_i = I-tauvv^T

    tau is a real scalar

    v is a real vector with v_i+1:n = 0 and v_i = 1

    v_1:i-1 is stored on return in submatrix A_{1:i-1, i+1}

    tau is stored on return in tau_i

    I is the identity matrix

    If uplo = 'U', then the following example shows the contents of A on return with n = 5:

    
    
    

    
    
    

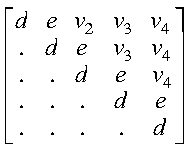
    where:

    d represents the diagonal elements of T

    e represents the superdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

  • For uplo = 'L', the matrix Q is the product of elementary reflectors: Q = H₁H₂ ...H_n-1,

    where:

    For each i: H_i = I-tauvv^T

    tau is a real scalar

    v is a real vector with v_1:i = 0 and v_i+1 = 1.

    v_i+2:n is stored on return in submatrix A_{i+2:n, i}

    tau is stored on return in tau_i

    I is the identity matrix.

    If uplo = 'L', then the following example shows the contents of A on return with n = 5:

    
    
    

    
    
    

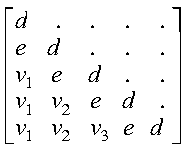
    where:

    d represents the diagonal elements of T

    e represents the subdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

Error Conditions

HPF-specific errors are listed below. Resource and input-argument errors listed in "Error Conditions" also apply to this subroutine.

Input-Argument Errors

Stage 1

1. The rank of the ultimate align target is greater than 2 for a, d, e, or tau.
2. The process rank is not the same for a, d, e, and tau.
3. The process rank is not 1 or 2 for a, d, e, or tau.

Stage 2

The process grid is not the same for a, d, e, and tau.

Stage 3

The data distribution is unsupported for a.

Stage 4

The data distribution is unsupported for d, e, or tau.

Stage 5

1. The shape of the assumed-shape arrays a, d, e, and tau is incompatible:
   1. size(a,1) <> size(a,2) or
   2. size(a,2) <> size(d) or
   3. size(d) <> size(e) or
   4. size(e) <> size(tau)
2. The shape of the assumed-shape array for a is invalid: size(a,1) <> size(a,2)
3. The column block size for a and the block sizes for d, e, and tau are incompatible.

Stage 6

1. The abstract process column indices for a, d, e, and tau are incompatible.
2. The data distribution for a is unsupported.

Example

This example shows the reduction of a symmetric matrix of order 4 to symmetric tridiagonal form. As in "Example", array data for A is block-cyclically distributed using a 2 × 2 process grid, with d, e, and tau replicated across each element of the corresponding column of A; that is, a copy of d, e, and tau is aligned with every row of A.

!HPF$ PROCESSORS PROC(2,2)
!HPF$ ALIGN D(:) WITH A(*,:)
!HPF$ ALIGN E(:) WITH A(*,:)
!HPF$ ALIGN TAU(:) WITH A(*,:)
!HPF$ DISTRIBUTE (CYCLIC, CYCLIC) ONTO PROC :: A
 
CALL SYTRD( A , D , E , TAU , 'U' )
-or-
CALL SYTRD( A , D , E , TAU , 'U' , INFO )

Input

Symmetric matrix A of order 4:

 *                    *
 | 5.0  4.0  1.0  1.0 |
 |  .   5.0  1.0  1.0 |
 |  .    .   4.0  2.0 |
 |  .    .    .   4.0 |
 *                    *

Output

Symmetric matrix A of order 4:

 *                            *
 | 1.00   0.00   0.41    0.22 |
 |  .     6.00   2.83    0.22 |
 |  .      .     7.00   -2.45 |
 |  .      .      .      4.00 |
 *                            *

Vector d of length 4:

 *                        *
 | 1.00  6.00  7.00  4.00 |
 *                        *

Vector e of length 4:

 *                           *
 | 0.00   0.00   2.83  -2.45 |
 *                           *

Vector tau of length 4:

 *                        *
 | 0.00  0.00  1.71  1.82 |
 *                        *

info = 0 (if info is present)

GEHRD--Reduce a General Matrix to Upper Hessenberg Form

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where A represents the general submatrix A_{ilo:ihi, ilo:ihi}. tau_1:ilo-1 and

If the assumed-shape array A has a size of zero, no computation is performed and the subroutine returns after doing some error checking. Then, if ihi = ilo, the subroutine returns after doing some parameter checking and setting tau_{ihi:size(tau)} to zero.

See references [13], [21], [31], and [41].

Table 137. Data Types

A, tau	Subroutine
Long-precision real	GEHRD

Syntax

On Entry

a

is the general matrix A.

Type: required

Specified as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 137, where size(a,1) = size(a,2).

tau

See 'On Return'.

ilo

lower range of the rows or columns in the general submatrix A used in the computation.

Type: optional

Default: ilo = 1

Specified as: a fullword integer; 1 <= ilo <= max(1,size(a,1)).

ihi

upper range of the rows or columns in the general submatrix A used in the computation.

Type: optional

Default: ihi = size(a,1)

Specified as: a fullword integer; min(ilo, size(a,1)) <= ihi <= size(a,1).

info

See 'On Return'.

On Return

a

is the general matrix A, containing the results of the computation.

The upper triangle and the first subdiagonal of A are overwritten by the corresponding elements of the upper Hessenberg matrix H. The elements below the first subdiagonal, with tau, represent the orthogonal matrix Q as a product of elementary reflectors.

See "Function", for more information.

Type: required

Returned as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 137.

tau

is the updated vector tau, where:

• tau_ilo:ihi-1 contains the scalar factors of the elementary reflectors.

• tau_1:ilo-1 are set to zero.

• tau_{ihi:size(tau)} are set to zero.

The elements of tau must be replicated across each element of the corresponding column of A; that is, a copy of tau is aligned with every row of A:

   !HPF$ ALIGN TAU(:) WITH A(*,:)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 137, where size(tau) = max(size(a,1)-1,0).

info

indicates that a successful computation occurred.

Type: optional

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

1. The assumed-shape arrays must have the exact size required for the computation, that is:
   • size(a,1) = size(a,2)
   • size(tau) = max(size(a,1)-1,0)

2. The assumed-shape arrays must have no common elements; otherwise, results are unpredictable.

3. On entry, A must already be:
   • Upper triangular in rows (1:ilo-1) and (ihi+1:size(a,1))
   • Upper triangular in columns (1:ilo-1) and (ihi+1:size(a,2))

   If this is not the case, do one of the following:

   • Do not specify the ilo and ihi arguments.
   • Set ilo = 1 and ihi = size(a,1).

   If you specify the ilo and ihi arguments, then:

   • If size(a,1) = 0, set ilo = 1 and ihi = 0.
   • If size(a,1) > 0, set 1 <= ilo <= ihi <= size(a,1).

4. For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"

5. Block-cyclic data distribution is required for your array data. Because data directives are included in the interface module PESSL_HPF, you can specify any data distribution for your vector and matrix, and the XL HPF compiler will, if necessary, redistribute the data prior to calling this subroutine. For how to code your HPF directives, see "Distributing Data in an HPF Program". For a sample program including directives, see Figure 9.

6. The restrictions given in "Notes and Coding Rules" also apply to this subroutine.

Function

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where:

• A represents the general submatrix A_{ilo:ihi, ilo:ihi}, where n = size(a,1) = size(a,2)
• Matrix Q is represented as a product of (ihi-ilo) elementary reflectors:

  Q = H_ilo H_ilo+1 ... H_ihi-1

  where:

  For each i: H_i = I-tauvv^T

  tau is a real scalar

  v is a real vector with v_1:i = 0, v_i+1 = 1, and v_ihi+1:n = 0

  v_i+2:ihi is stored on return in A_{i+ilo+1:ihi, ilo+i-1}

  tau is stored on return in tau_i+ilo-1

  I is the identity matrix

  The following example shows the contents of the general submatrix A, within a matrix of order 7, on entry with ilo = 2 and ihi = 6:

  
  
  

  
  
  

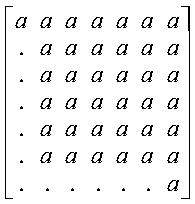
  Following is the general submatrix A on return:

  
  
  

  
  
  

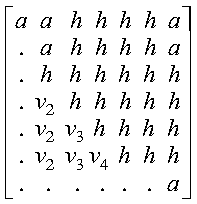
  where:

  a represents an element of the original submatrix A.

  h represents a updated element of the upper Hessenberg matrix H.

  v_i represents the corresponding elements of the vector defining H_ilo+i-1.

Error Conditions

HPF-specific errors are listed below. Resource and input-argument errors listed in "Error Conditions" also apply to this subroutine.

Input-Argument Errors

Stage 1

1. The rank of the ultimate align target is greater than 2 for a or tau.
2. The process rank is not the same for a and tau.
3. The process rank is not 1 or 2 for a or tau.

Stage 2

The process grid is not the same for a and tau.

Stage 3

The data distribution is unsupported for a.

Stage 4

The data distribution is unsupported for tau.

Stage 5

1. The shape of the assumed-shape arrays a and tau is incompatible:
   1. size(a,1) <> size(a,2) or
   2. size(tau) <> max (size(a,1)-1,0)
2. The shape of the assumed-shape array for a is invalid: size(a,1) <> size(a,2)
3. size(tau) <> 0, and the column block size for a and the block size for tau are incompatible.

Stage 6

1. ilo is present, and ilo < 1 or ilo > max(1,size(a,1)).

2. ihi is present, and ihi < min(ilo, size(a,1)) or ihi > size(a,1)

Stage 7

1. size(tau) <> 0, and the abstract process column indices for a and tau are incompatible.

2. The data distribution for a is unsupported.

Example

This example shows the reduction of a general matrix of order 3 to upper Hessenberg form. As in "Example", array data for A is block-cyclically distributed using a 2 × 2 process grid, with tau replicated across each element of the corresponding column of A; that is, a copy of tau is aligned with every row of A.

!HPF$ PROCESSORS PROC(2,2)
!HPF$ ALIGN TAU(:) WITH A(*,:)
!HPF$ DISTRIBUTE (CYCLIC, CYCLIC) ONTO PROC :: A
 
CALL GEHRD( A , TAU )
-or-
CALL GEHRD( A , TAU , 1 , 3 , INFO )

Input

General matrix A of order 3:

 *                     *
 |  33.0   16.0   72.0 |
 | -24.0  -10.0  -57.0 |
 |  -8.0   -4.0  -17.0 |
 *                     *

Output

General matrix A of order 3:

 *                       *
 | 33.00  -37.95   63.25 |
 | 25.30  -29.00   53.00 |
 |  0.16    0.00    2.00 |
 *                       *

Vector tau of length 2:

 *            *
 | 1.95  0.00 |
 *            *

info = 0 (if info is present)

GEBRD--Reduce a General Matrix to Bidiagonal Form

This subroutine reduces a real general matrix A to upper or lower bidiagonal form B by an orthogonal transformation:

B = Q^TAP

where:

• If size(a,1) >= size(a,2), then B is upper bidiagonal.
• If size(a,1) < size(a,2), then B is lower bidiagonal.

If the assumed-shape array for A has a size of zero, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13], [21], [31], and [41].

Table 138. Data Types

A, d, e, tauq, taup	Subroutine
Long-precision real	GEBRD

Syntax

On Entry

a

is the general matrix A.

Type: required

Specified as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 138.

d

See 'On Return'.

e

See 'On Return'.

tauq

See 'On Return'.

taup

See 'On Return'.

info

See 'On Return'.

On Return

a

is the updated general matrix A, containing the results of the computation, where:

• If size(a,1) >= size(a,2), the diagonal and first superdiagonal of A are overwritten by the corresponding elements of the upper bidiagonal matrix B. The elements below the diagonal, with tau_q, represent the orthogonal matrix Q as a product of elementary reflectors. The elements above the first superdiagonal, with tau_p, represent the orthogonal matrix P as a product of elementary reflectors.

• If size(a,1) < size(a,2), the diagonal and first subdiagonal of A are overwritten by the corresponding elements of the lower bidiagonal matrix B. The elements below the first subdiagonal, with tau_q, represent the orthogonal matrix Q as a product of elementary reflectors. The elements above the diagonal, with tau_p, represent the orthogonal matrix P as a product of elementary reflectors.

See "Function", for more information.

Type: required

Returned as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 138.

d

is the updated vector d, where:

• If size(a,1) >= size(a,2), then d contains the diagonal elements of the bidiagonal matrix B.

  The elements of d must be replicated across each element of the corresponding column of A; that is, a copy of d is aligned with every row of A:

     !HPF$ ALIGN D(:) WITH A(*,:)
  

• If size(a,1) < size(a,2), then d contains the diagonal elements of the bidiagonal matrix B.

  The elements of d must be replicated across each element of the corresponding row of A; that is, a copy of d is aligned with every column of A:

     !HPF$ ALIGN D(:) WITH A(:,*)
  

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 138, where size(d) = min(size(a,1), size(a,2)).

e

is the updated vector e, where:

• If size(a,1) >= size(a,2), then e contains the superdiagonal elements of the bidiagonal matrix B.

  The elements of e must be replicated across each element of the corresponding row of A; that is, a copy of e is aligned with every column of A:

     !HPF$ ALIGN E(:) WITH A(:,*)
  

• If size(a,1) < size(a,2), then e contains the subdiagonal elements of the bidiagonal matrix B.

  The elements of e must be replicated across each element of the corresponding column of A; that is, a copy of e is aligned with every row of A:

     !HPF$ ALIGN E(:) WITH A(*,:)
  

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 138, where size(e) = max(min(size(a,1), size(a,2))-1, 0).

tauq

is the updated matrix tau_q, containing the scalar factors of the elementary reflectors which represent the orthogonal matrix Q. See "Function" for more details.

The elements of tau_q must be replicated across each element of the corresponding column of A; that is, a copy of tau_q is aligned with every row of A:

   !HPF$ ALIGN TAUQ(:) WITH A(*,:)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 138, where size(tauq) = min(size(a,1), size(a,2)).

taup

is the updated matrix tau_p, containing the scalar factors of the elementary reflectors which represent the orthogonal matrix P. See "Function" for more details.

The elements of tau_p must be replicated across each element of the corresponding row of A; that is, a copy of tau_p is aligned with every column of A:

   !HPF$ ALIGN TAUP(:) WITH A(:,*)

Type: required

Returned as: an assumed-shape array with shape (:), containing numbers of the data type indicated in Table 138, where size(taup) = min(size(a,1), size(a,2)).

info

indicates that a successful computation occurred.

Type: optional

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

1. The assumed-shape arrays must have the exact size required for the computation, that is:
   • size(d) = min(size(a,1), size(a,2))
   • size(e) = max(min(size(a,1), size(a,2))-1, 0)
   • size(tauq) = min(size(a,1), size(a,2))
   • size(taup) = min(size(a,1), size(a,2))

2. Data directives for this subroutine cannot be included in the interface module PESSL_HPF, because the alignment requirements for d and e depend on the size of the matrix A; therefore, you must code the data directives for all the assumed-shape arrays explicitly in your program according to the rules described above.

   Block-cyclic data distribution is required for your array data. For how to code your HPF directives, see "Distributing Data in an HPF Program". For a sample program including directives, see Figure 9.

3. The assumed-shape arrays must have no common elements; otherwise, results are unpredictable.

4. For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"

5. The restrictions given in "Notes and Coding Rules" also apply to this subroutine.

Function

This subroutine reduces a real general matrix A to upper or lower bidiagonal form B by an orthogonal transformation:

B = Q^TAP

where:

• A is a general matrix, where m = size(a,1) and n = size(a,2).
• If m >= n, then B is upper bidiagonal, and matrices Q and P are represented as the product of elementary reflectors:

  Q = H₁ H₂ ... H_n

  P = G₁ G₂ ... G_n-1

  where:

  For each i: H_i = I-tau_qvv^T

  For each i: G_i = I-tau_puu^T

  tau_q and tau_p are real scalars, where:

  
  
  

  
  
  

  v is a real vector with v_1:i-1 = 0 and v_i = 1

  v_i+1:m is stored on return in submatrix A_{i+1:m, i}

  u is a real vector with u_1:i = 0 and u_i+1 = 1

  u_i+2:n is stored on return in submatrix A_{i, i+2:n}

  I is the identity matrix

  The following example shows the contents of A on return with m = 6 and n = 5:

  
  
  

  
  
  

  where:

  d represents the diagonal elements of B

  e represents the off-diagonal elements of B

  v_i represents the corresponding elements of the vector defining H_i.

  u_i represents the corresponding elements of the vector defining G_i.

• If m < n, then B is lower bidiagonal, and matrices Q and P are represented as the product of elementary reflectors:

  Q = H₁ H₂ ... H_m-1

  P = G₁ G₂ ... G_m

  where:

  For each i: H_i = I-tau_qvv^T

  For each i: G_i = I-tau_puu^T

  tau_q and tau_p are real scalars, where:

  
  
  

  
  
  

  v is a real vector with v_1:i = 0 and v_i+1 = 1

  v_i+2:m is stored on return in submatrix A_i+2:m,i

  u is a real vector with u_1:i-1 = 0 and u_i = 1

  u_i+1:n is stored on return in submatrix A_i,i+1:n

  I is the identity matrix

  The following example shows the contents of A on return with m = 5 and n = 6:

  
  
  

  
  
  

  where:

  d represents the diagonal elements of B

  e represents the off-diagonal elements of B

  v_i represents the corresponding elements of the vector defining H_i.

  u_i represents the corresponding elements of the vector defining G_i.

Error Conditions

HPF-specific errors are listed below. The input-argument errors and computational errors listed in "Error Conditions" also apply to this subroutine.

Input-Argument Errors

Stage 1

1. The rank of the ultimate align target is greater than 2 for a, d, e, tauq, or taup.
2. The process rank is not the same for a, d, e, tauq, and taup.
3. The process rank is not 1 or 2 for a, d, e, tauq, or taup.

Stage 2

The process grid is not the same for a, d, e, tauq, and taup.

Stage 3

The data distribution is unsupported for a.

Stage 4

The data distribution is unsupported for d, e, tauq, or taup.

Stage 5

1. The shape of the assumed-shape arrays a, d, e, tauq, and taup is incompatible:
   1. size(d) <> min(size(a,1), size(a,2)) or
   2. size(e) <> max(min(size(a,1), size(a,2))-1, 0) or
   3. size(tauq) <> min(size(a,1), size(a,2)) or
   4. size(taup) <> min(size(a,1), size(a,2))
2. The block sizes for d, e (if size(e) <> 0), tauq, and taup are incompatible with the corresponding row or column block size of a.

Stage 6

1. The abstract process indices for a, d, e (if size(e) <> 0), tauq, and taup are incompatible.
2. The data distribution for a is unsupported.

Example

This example shows the reduction of a general matrix of order 4 by 3 to bidiagonal form. As in "Example", array data for A is block-cyclically distributed using a 2 × 2 process grid, with:

• tau_q and d replicated across each element of the corresponding column of A; that is, a copy of tau_q and d is aligned with every row of A.

• tau_p and e replicated across each element of the corresponding row of A; that is, a copy of tau_p and e is aligned with every column of A.

!HPF$ PROCESSORS PROC(2,2)
!HPF$ ALIGN D(:) WITH A(*,:)
!HPF$ ALIGN E(:) WITH A(:,*)
!HPF$ ALIGN TAUQ(:) WITH A(*,:)
!HPF$ ALIGN TAUP(:) WITH A(:,*)
!HPF$ DISTRIBUTE (CYCLIC, CYCLIC) ONTO PROC :: A
 
CALL GEBRD( A , D , E , TAUQ , TAUP )
-or-
CALL GEBRD( A , D , E , TAUQ , TAUP , INFO )

Input

General matrix A of order 4 × 3:

 *                  *
 | 10.0   5.0   9.0 |
 |  2.0  16.0  10.0 |
 |  3.0   7.0  21.0 |
 |  4.0   8.0  12.0 |
 *                  *

Output

General matrix A of order 4 × 3:

 *                      *
 | -11.36  22.80   0.56 |
 |   0.09  23.32   1.67 |
 |   0.14   0.46  -9.68 |
 |   0.19   0.22   0.08 |
 *                      *

Vector d of length 3:

 *                      *
 | -11.36  23.32  -9.68 |
 *                      *

Vector e of length 2:

 *       *
 | 22.80 |
 |  1.67 |
 *       *

Vector tau_q of length 3:

 *                  *
 | 1.88  1.59  1.99 |
 *                  *

Vector tau_p of length 3:

 *      *
 | 1.52 |
 | 0.00 |
 | 0.00 |
 *      *

info = 0 (if info is present)