
That is, the physical properties of the beam do not depend on the direction:
| Note: | The bar over a variable indicates it has dimension; whereas, the unbarred form is dimensionless. |
Both a message passing Fortran 90 sample program and an HPF sample program are presented in this section, along with the commands for processing them in a parallel processing environment. The sample programs, solving a thermal diffusion problem, use vectors and matrices distributed across a one-dimensional process grid and call Level 2 PBLAS, Eigensystem analysis, and Fourier transform subroutines.
A copy of these sample programs, plus an equivalent C program, are provided with the Parallel ESSL product. For file names and installation procedures, see the Parallel ESSL Installation Memo.
Following is a table of contents for this section, along with a description
of each section for both the message passing Fortran 90 sample program and the
HPF sample program.
Table 144. Table of Contents for the Sample Thermal Diffusion Programs
| Contents | Page (Message Passing) | Page (HPF) |
|---|---|---|
| Thermal Diffusion Discussion Paper: A technical description of the problem to be solved. | "Thermal Diffusion Discussion Paper" | "Thermal Diffusion Discussion Paper" |
| Program main: Finds the cooling rate for a specified set of points in an anisotropic rectangular beam, immersed in a constant heat bath with a temperature of zero. | "Program Main (Message Passing)" | "Program Main (HPF)" |
| Module parameters: Defines system wide parameters and the index structure used to help map global indices to local indices. | "Module Parameters (Message Passing)" | "Module Parameters (HPF)" |
Module diffusion: Assigns problem parameters and initial
data.
| "Module Diffusion (Message Passing)" | "Module Diffusion (HPF)" |
Module fourier: Represents both the diffusion operator
and the temperature profile in a sine function basis.
| "Module Fourier (Message Passing)" | "Module Fourier (HPF)" |
Module scale: Initializes the communications and
provides a few communication utility routines.
| "Module Scale (Message Passing)" | -- |
| Input Data: Sample input data in namelist format, used by subroutine init_diffusion in module diffusion. | "Input Data" | "Input Data" |
| Output Data: Sample output data, based on the sample input data, issued at the end of program main. | "Output Data" | "Output Data" |
| Makefile: The makefile used to build the thermal diffusion program. | "Makefile (Message Passing)" | "Makefile (HPF)" |
| Run Script: The script file used to execute the thermal diffusion program. | "Run Script" | "Run Script" |
The objective of the diffusion program is to solve for the temperature of a beam at any point and at any time, given an initial temperature distribution. The following assumptions are made concerning the beam and its properties:

That is, the physical properties of the beam do not depend on the direction:
| Note: | The bar over a variable indicates it has dimension; whereas, the unbarred form is dimensionless. |
The general diffusion equation is given by:
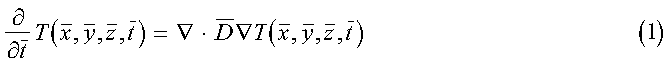
where:
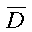
is the position-dependent diffusion coefficient. Equation 1 may be rewritten, ignoring the z dimension, using the following dimensionless variables:
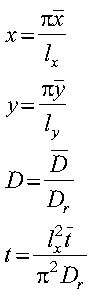
as follows:
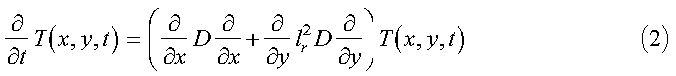
where Dr is a reference diffusion constant, and lr is the beam dimension ratio lx/ly. This equation is subject to the initial and boundary conditions given by:
In the program, the initial condition T0(x, y), the diffusion coefficient D(x, y), and the ratio lr are determined in the initialization subroutine init_diffusion. nx and ny, defined later, are also initialized here. Equation 2 is solved by representing the operators in a sine function basis and solving the resulting matrix equations. We begin by expanding T in sine functions, as follows:
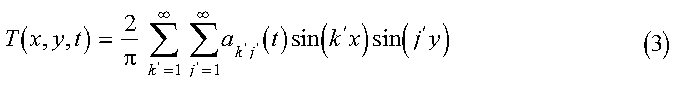
The initial set of expansion coefficients akj(0) are determined from the initial temperature profile by:
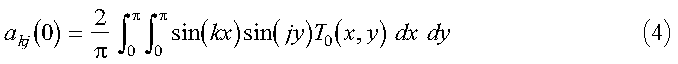
where the orthogonality of the sine functions has been used. If we extend the range of T from pi to 2pi, as an odd function, equation 4 can be written in terms of a discrete Fourier transform:
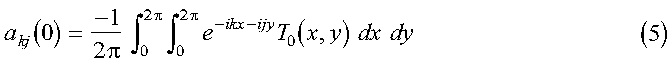
akj(0) is calculated in the program in the subroutine expand_temp_profile, with the actual temperatures calculated in the function init_temp. The subroutine call to DCFT2 performs the Fourier transform, and the results are stored in the array A. Substitute equation 3 into equation 2, multiply by (2/pi)sin(kx)sin(jy) and integrate over x and y to obtain:
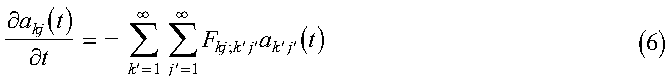
where:
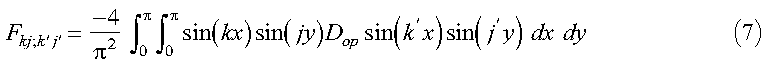
and:

Note that sin(kx)sin(k'x) and sin(jy)sin(j'y) are even functions about pi. Therefore, if we define D(2pi-x, y) = D(x, y) and D(x, 2pi-y) = D(x, y), where 0 <= x <= pi and 0 <= y <= pi, the limits on the integral in equation 7 may be extended to 2pi:
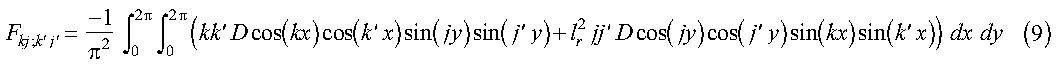
Equation 9 may be further reduced to sums of Fourier transforms using the identities:
Substituting these identities into equation 9, we have:
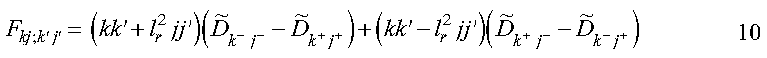
where:
and where:
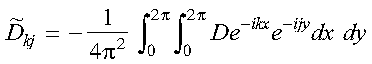
Equation 10 is the simplest form for the matrix elements of the diffusion operator, and these elements are calculated in the subroutine get_diffusion_matrix. The diffusion coefficient is evaluated with the function diff_coef. The Parallel ESSL Fourier transform subroutine PDCFT2, called in subroutine get_diffusion_matrix, is used to determine the following elements:
which are stored in the array DF. Because DF is an array which is block cyclically distributed among the nodes and each node requires elements of DF not locally available, this array is collected to the global array DFG on each node. The array DFG is subsequently used to calculate the matrix F. Now that we have determined the matrix elements of equation 6, we must truncate it in order to solve it. This may be done by truncating the k summation at nx and the j summation at ny. The dual indices may be collapsed into a single index 1 by:
The j and k indices can similarly be recovered from the 1 index by:
Rewriting the truncated equation 6, we have:

Equation 11 has the general solution:
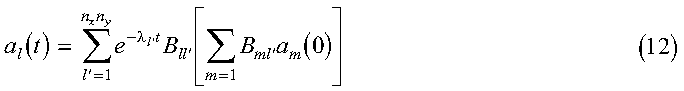
where lambda is the eigenvalue vector and B is the matrix of eigenvectors of the matrix F. The eigenvectors B and eigenvalues lambda correspond to the arrays B and LAMBDA in the program. These eigenvalues and eigenvectors are determined with the Parallel ESSL subroutine PDSYEVX. The inner sum:
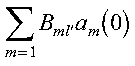
corresponds to the array AB, with ABT containing the extra factor of:
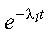
Also, al(t) is represented by the array X, which is reused for each solution time.
Each of these matrix multiplications are done using the Parallel ESSL subroutine PDGEMV. The final solution is obtained by summing over the expansion coefficients:
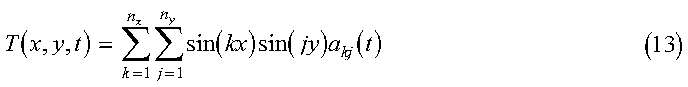
The final temperature array is TEMP in the program, with the indices into the array corresponding to specific values of x, y, and t.
program main
!
! Purpose, to find the cooling rate for a specified set of
! points in an anisotropic rectangular beam, immersed in a constant
! heat bath with a temperature of 0.
!
! Routines called:
! expand_temp_profile
! get_diffusion_matrix
! igamx2d
! init_diffusion
! initialize_rarray
! initialize_scale
! pdgemv
! pdsyevx
! rlocal_to_rglobal
!
use parameters
use scale
use diffusion
use fourier
implicit none
integer :: n, ix, jx, iy, jy, k, i, j, stat, it, ib, ig
integer :: num_errors, lwork, ilwork
integer, allocatable :: iwork(:)
real(long), allocatable :: work(:)
!
! a contains the sine expansion coefficients of the initial
! temperature profile.
! b contains the eigenvectors of the diffusion operator in the
! sine function basis.
! ab contains the initial temperature profile expanded in the
! eigenvectors of the diffusion operator.
! f contains the matrix elements of the diffusion operation in
! sine function basis.
! lambda contains the eigenvalues of the diffusion operator.
!
! df contains the Fourier transform of the diffusion coefficient function.
!
real(long), allocatable :: lambda(:), xg(:,:)
real(long), allocatable :: gap(:)
real(long) :: dum
real(long), pointer :: f(:,:), b(:,:), a(:,:)
type (g_index), pointer :: f_i, b_i, a_i
integer :: f_d(DESC_DIM), b_d(DESC_DIM), a_d(DESC_DIM)
real(long), pointer :: x(:,:), ab(:,:), abt(:,:)
type (g_index), pointer :: x_i, ab_i, abt_i
integer :: x_d(DESC_DIM), ab_d(DESC_DIM), abt_d(DESC_DIM)
real(long), allocatable :: xsines(:,:), ysines(:,:), temp(:,:)
integer, allocatable :: ifail(:), iclustr(:)
integer :: biga_index, num_eigvalues, num_vectors, info
!
! Read in the problem size, initialize the problem dimensions,
! choose functional form for the spatially dependent heat diffusion
! coefficients, choose functional form of initial temperature distribution
! and choose the number of points, in both space and time, of the solution
! to print out.
!
call init_diffusion
num_errors = 0
!
! Read in how many sine functions to include in both the
! x and y directions.
!
! Because we need to get the Fourier coefficients of the sums
! and differences of the indices, we need to include twice as
! many Fourier coefficients as the number of sine expansion coefficients.
! Also, because the top and bottom halves of the Fourier
! transform are identical,
! an artifact of artificially extending the diffusion coefficient
! function and the initial temperature distribution, we need to
! double the number of Fourier coefficients again. Finally, the
! extra sum of one comes from the fact that the sine function
! expansion starts a 1 and the Fourier expansion starts at 0.
!
! n is the order of the diffusion operator equation.
n = dif_nx * dif_ny
!
! Initialize BLACS and calculate default block sizes.
!
call initialize_scale(n, biga_index)
!
!
! Allocate room for the eigenvalues of diffusion operator.
!
allocate( lambda(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for sines of x and y coordinates.
!
allocate( xsines(dif_npts, dif_nx) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( ysines(dif_npts, dif_ny) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for temperature history at selected points.
!
allocate( temp(dif_npts, dif_ntemps) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for global temperature profile expansion vector at time t.
!
allocate( xg(1, n) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
call igamx2d(sc_icontext,'A',' ',1,1,num_errors,1,-1,-1,-1, &
& -1,-1)
if( num_errors .gt. 0 ) then
if( sc_iam .eq. 0 ) then
write(*,*) 'Error in allocating arrays in main'
call blacs_abort(sc_icontext, 1)
endif
endif
!
! A call to expand_temp_profile returns the sine expansion
! coefficients of the initial temperature profile.
!
!
! Get matrices.
!
! Diffusion operator matrix.
call initialize_rarray(f, f_d, f_i, n, n, biga_index)
! Eigenvectors of diffusion operator matrix.
call initialize_rarray(b, b_d, b_i, n, n, biga_index)
! Initial temperature profile, in row vector.
call initialize_rarray(a, a_d, a_i, 1, n, biga_index)
! Initial temperature profile, in eigenfunction basis, in row vector.
call initialize_rarray(ab, ab_d, ab_i, 1, n, biga_index)
! Temperature profile, at time t, in eigenfunction basis, in row vector.
call initialize_rarray(abt, abt_d, abt_i, 1, n, biga_index)
! Temperarure profile in at time t in sine expansion basis, in row vector.
call initialize_rarray(x, x_d, x_i, 1, n, biga_index)
!
! Represent initial temperature in sine function expansion.
!
call expand_temp_profile(a,a_i,a_d)
!
! Here, we are calculating the initial set of coefficients
! in the sine function expansion as given in equations 3 and 4 of
! the discussion paper
!
!
! The call to get_diffusion_matrix returns the diffusion
! operator in the sine function basis.
!
call get_diffusion_matrix(f,f_i,f_d)
!
! This last call determines the matrix elements defined by equation 10
! in the discussion paper.
!
!
! Here we precalculate the sine functions, sin(kx) and sin(jy) used
! in equation 13 of the discussion paper.
! These sine functions are only evaluated at the points x and y for
! which the solution is evaluated.
!
do i = 1, dif_nx
do j = 1, dif_npts
xsines(j,i) = sqrt(2.d0/pi) * sin( i * dif_x(j))
enddo
enddo
do i = 1, dif_ny
do j = 1, dif_npts
ysines(j,i) = sqrt(2.d0/pi) * sin( i * dif_y(j))
enddo
enddo
!
! Allocate arrays for eigenvalue decomposition.
!
allocate( ifail(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
allocate( iclustr(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
allocate( gap(sc_nnodes), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate scratch space for the symetric eigenvector solver.
!
lwork = 20*n + max( 5*n, n*(n+ sc_nnodes-1)/sc_nnodes ) &
& + n*( (n+ sc_nnodes-1)/sc_nnodes) + 2*f_d(MB_) * f_d(MB_)
ilwork = 2*n + max((3*n+1+sc_nnodes),max(4*n,14))
allocate( work(lwork) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( iwork(ilwork) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
!
! Test to see if we had any allocation errors.
!
call igamx2d(sc_icontext,'A',' ',1,1,num_errors,1,-1,-1,-1, &
& -1,-1)
if( num_errors .gt. 0 ) then
if( sc_iam .eq. 0 ) then
write(*,*) 'Error in allocating arrays for pdsyevx in ', &
& 'main'
call blacs_abort(sc_icontext, 1)
endif
endif
do i = 1, sc_nnodes
gap(i) = 0.d0
enddo
do i = 1, n
ifail(i) = 0
iclustr(i) = 0
enddo
!
! The call to pdsyevx will find both the eigenvalues and eigenvectors
! of the diffusion matrix operator f. The eigenvalues will be stored in
! the vector lambda and the corresponding eigenvectors will be stored in
! the matrix b. The f and b matrices in the program correspond to the
! F and B matrices in equations 11 and 12 in the
! discussion paper.
!
!
call pdsyevx('V','A','U',n,f,1,1,f_d,-1.d30,1.d30,0,n, &
& 0.d0,num_eigvalues,num_vectors,lambda,1.d-5,b,1,1,b_d, &
& work, lwork, iwork, ilwork, ifail, iclustr, gap, info)
if( sc_iam .eq. 0) then
if( info .ne. 0 ) then
write(*,*) ' info is ', info
call blacs_abort(sc_icontext, 1)
endif
endif
!
! Multiply the transpose of the eigenvector matrix, b, with the sine
! expansion of the initial temperature profile, a, to obtain the
! initial temperature profile in terms of the eigenfuctions of the
! diffusion operator.
!
call pdgemv('T', n, n, 1.d0, b, 1, 1, b_d, a, 1, 1, a_d, 1, &
& 0.d0, ab, 1, 1, ab_d, 1)
!
! This first matrix multiplication, yielding the matrix ab,
! corresponds to the inner summation in equation 10
! of the discussion paper.
!
!
! Calculate temperature profile for each time step.
!
do it = 1, dif_ntemps
i = 0
do ib = 1, ab_i%num_col_blks
do ig = ab_i%scb(ib), ab_i%ecb(ib)
i = i + 1
abt(1,i) = exp( -lambda(ig) * it * dif_delta_t) * ab(1,i)
enddo
enddo
!
! abt now has the expansion of the temperature profile in terms of the
! eigenvectors of the diffusion operator.
!
!
! Multiply the eigenvector matrix with abt to give the sine function
! expansion of the temperature profile at time t, x.
!
call pdgemv('N', n, n, 1.d0, b, 1, 1, b_d, abt, 1, 1, abt_d, &
& 1, 0.d0, x, 1, 1, x_d, 1)
! This last sum corresponds to the outer sum of equation 12, where the
! time dependent expansion coefficients a{sub l}(t) are stored in the
! temporary array x in the program.
!
!
! Gather all of the local pieces of the array x to the array xg.
!
call rlocal_to_rglobal(x, x_d, xg )
do k = 1, dif_npts
temp(k, it) = 0.d0
enddo
do iy = 1, dif_ny
do ix = 1, dif_nx
i = (iy -1) * dif_nx + ix
do k = 1, dif_npts
temp(k,it) = temp(k,it) + xsines(k,ix) * ysines(k,iy) &
& * xg(1,i)
enddo
enddo
enddo
!
! This last do loop corresponds to the double summation in equation
! 13 of the discussion paper.
!
enddo ! end of time loop
!
! Here, we are just writing out the temperatures at the selected times
! and points.
!
if( sc_iam .eq. 0 ) then ! if I am node 0
write(*,*) ' point # X Y'
do i = 1, dif_npts
write(*,'(2x, i6, 2x, 2f11.4)') i, dif_x(i), dif_y(i)
enddo
write(*,*)
do k = 1, dif_npts, 6
write(*,*)
write(*,'(30X,'Points'')')
write(*,'('' TIME '',6(5x,''#'', i4))') (i, i=k, k+5)
do i = 1, dif_ntemps
write(*,'(7f10.5)') i*dif_delta_t, &
& (temp(j,i),j=k,min(k+5,dif_npts))
enddo
enddo
endif
deallocate(xg)
deallocate(xsines)
deallocate(ysines)
deallocate(lambda)
deallocate(temp)
deallocate( ifail)
deallocate( iclustr)
deallocate( gap)
stop
end
module parameters
!
! Purpose: Define system wide parameters and index structure
! used to help map global indices to local indices.
!
implicit none
public
integer, parameter :: long=8, short=4
real(long), parameter :: pi = 3.141592653589793d0
real(long), parameter :: twopi = 2.d0*pi
type g_index
integer :: num_row_blks, num_col_blks
integer, pointer :: srb(:), scb(:), erb(:), ecb(:)
end type g_index
!
! The g_index type was created for convenience
! components:
! num_row_blks: number of block repetitions over matrix rows.
! num_col_blks: number of block repetitions over matrix columns.
! srb: global row index at start of a block
! corresponding local index is ( block # -1) * mb
! where mb is the number of rows in the block.
!
! scb: global column index at start of a block
! corresponding local index is ( block # -1) * nb
! where nb is the number of columns in the block.
!
! erb: last global row index in the block.
! ecb: last global column index in the block.
public g_index
end module parameters
module diffusion
!
! Purpose: Assign problem parameters and initial data.
!
! Routines called:
! none
!
use parameters
use scale
implicit none
private
!
! Make all entities private by default.
! Have all public entities have the prefix dif_.
!
! The following are the publicly available routines.
!
public init_diffusion, init_temp, diff_coef
!
! The following are publicly available variables.
!
real, public :: dif_ly_ratio
integer, public :: dif_nx, dif_ny, dif_npts, dif_ntemps
real(long), public :: dif_delta_t
real(long), public, allocatable :: dif_x(:), dif_y(:)
!
! dif_ly_ratio is the ratio of the x and y lengths of the beam.
! dif_nx is the number of sine expansion coefficients to use
! in the x direction.
! dif_ny is the number of sine expansion coefficients to use
! in the y direction.
! dif_delta_t is the size of the time step to be display on output.
! dif_ntemps is the total number of temperatures to display per point.
! dif_npts is the total number of points to output.
! dif_x is the x coordinates of the points.
! dif_y is the y coordinates of the points.
!
!
!
! Private variables
!
integer :: init_f=1, diff_f=1
! init_f chooses the functional form of initial distribution of temperature.
! diff_f chooses the functional form for spatially dependent head diffusion
! coefficient.
contains
!****************************************************************************!
!* *!
!* Module routine init_diffusion *!
!* *!
!* Purpose: Initialize problem size, number of output point and *!
!* functional form of diffusion constant and initial temperature *!
!* distribution *!
!* *!
!****************************************************************************!
subroutine init_diffusion
namelist /input/ ly_ratio, delta_t, numx, numy, nx, ny, numt, &
& init_f, diff_f
integer :: numx=5, numy=5, nx=7, ny=7, numt=20
real(long) :: ly_ratio=1.d0, delta_t=0.1
real(long) :: delx, dely
integer :: i, j, ij
logical :: ex
!==============================================================================!
! Start of executable code !
inquire ( file='diffus.naml', exist=ex)
if( ex ) then
open( 10, file='diffus.naml', action='read')
read( 10, input)
close(10)
endif
dif_ly_ratio = ly_ratio
dif_npts = numx*numy
dif_delta_t = delta_t
dif_ntemps = numt
dif_nx = nx
dif_ny = ny
allocate( dif_x(numx*numy) )
allocate( dif_y(numy*numx) )
!
! Assign a simple linear array of points.
!
delx = PI/ ( numx + 1.d0)
dely = PI/ ( numy + 1.d0)
do i = 1, numx
do j = 1, numy
ij = numx*(j-1) + i
dif_x(ij) = delx* i
dif_y(ij) = dely * j
enddo
enddo
return
end subroutine init_diffusion
!****************************************************************************!
!* *!
!* Module routine init_temp *!
!* *!
!* Purpose: Return the initial temperature of the bar at a particular *!
!* point *!
!* *!
!****************************************************************************!
function init_temp(x, y)
!
! Arguments:
! x: real*8 (in), x coordinate
! y: real*8 (in), y coordinate
! Function return:
! init_temp: real*8 (out), initial temperature at (x,y)
!
real(long), intent(in) :: x, y
real(long) :: init_temp
!
! The problem has been scaled to go from 0 to pi in both the x
! and y directions. To calculate the expansion coefficients, we
! define the function to be odd about pi and use the range 0 < x < 2*pi
!
! Local variables.
integer :: isign
real(long) :: x1, y1
!
isign = 1
x1 = x
if( x .gt. pi ) then
isign = -isign
x1 = twopi - x
endif
y1 = y
if( y .gt. pi ) then
isign = -isign
y1 = twopi - y
endif
!
! Choose very simple temperature profile cases.
!
select case (init_f)
case (1)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)
case (2)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*y1
case (3)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*x1
case (4)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*x1*y1
case (5)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)
case (6)
init_temp = isign*(x1*(pi-x1))**2 *y1*(pi-y1)
case (7)
init_temp = isign*(x1*(pi-x1))*(y1*(pi-y1))**2
case default
init_temp = isign*sin(x1)*sin(y1)
end select
return
end function init_temp
!****************************************************************************!
!* *!
!* Module routine diff_coef *!
!* *!
!* Purpose: Return the value of the thermal diffusion coefficient at *!
!* an arbitrary point *!
!* *!
!****************************************************************************!
function diff_coef(x, y)
! Arguments:
! x: real*8 (in), x coordinate
! y: real*8 (in), y coordinate
! Function return:
! diff_coef: real*8 (out), diffusion coefficient at (x,y)
!
real(long), intent(in) :: x, y
real(long) :: diff_coef
!
! The problem has been scaled to go from 0 to pi in both the x
! and y directions. To simplify the matrix element calculations,
! we define the function to be even about pi.
!
! Local variables.
real(long) :: x1, y1
!==============================================================================!
! Start of executable code. !
x1 = x
if( x .gt. pi ) x1 = twopi - x
y1 = y
if( y .gt. pi ) y1 = twopi - y
!
! Choose very simple diffusion coefficient cases.
!
select case (diff_f)
case (1)
diff_coef = .5d0 + (x1 + y1) / (2 * twopi)
case (2)
diff_coef = ((1.d0 + x1)*(pi - x1 + 1.d0)*(y1 + pi))/ 3*pi
case (3)
diff_coef = (y1 + pi) * pi/((pi + x1) * (2* pi - x1))
case default
diff_coef = 1.d0
end select
return
end function diff_coef
end module diffusion
module fourier
!
! Purpose: To represent both the diffusion operator and
! the temperature profile in a sine function basis.
!
! Routines called:
! blacs_abort
! clocal_to_rglobal
! dcft2
! igamx2d
! initialize_carray
! initialize_scale
! pdcft2
!
use parameters
use scale
use diffusion
implicit none
private
!
! all entities private by default
!
external pdcft2
!
! publicly available routines
!
public expand_temp_profile, get_diffusion_matrix
public g_index
!
! publicly available variables
!
!
! private variables
!
integer :: pn_fac(5) = 5*0 ! prime factors of number of nodes
! nnodes = 2**pn_fac(1) * 3**pn_fac(2) * 5**pn_fac(3) *
! 7**pn_fac(4) * 11**pn_fac(5)
!
! private routines
!
private minpower2, factor_nodes
contains
!****************************************************************************!
!* *!
!* Module routine get_diffusion_matrix *!
!* *!
!* Purpose: To obtain the matrix representation of the diffusion *!
!* operator in a sine function basis *!
!* *!
!****************************************************************************!
subroutine get_diffusion_matrix(f,f_i, f_d)
!
! Arguments:
! f: real*8,dimension(:,:),(out), local part of the global matrix
! containing the diffusion operator in sine function basis.
! f_d: integer*4, dimension(:),(in), array descriptor for f.
! f_i: g_type, (in), g_type structure for f, see parameter.f.
!
real(long), intent(out) :: f(:,:)
integer, intent(in) :: f_d(DESC_DIM)
type (g_index), intent(in) :: f_i
! Local variables
!
! df contains the diffusion coefficient before the call to pdcft2.
! df contains the Fourier transpose of diffusion coefficients after the call.
! dfg contains the entire Fourier transpose of df on each node.
!
complex(long), pointer :: df(:,:)
type (g_index), pointer :: df_i
integer :: df_d(DESC_DIM)
real(long), allocatable :: dfg(:,:)
!
! ixi and iyi are arrays which, given a global index,
! return the x and y offsets. Recall that the large arrays
! are 4 dimensional arrays collapsed into 2 dimensions,
! where i = (ix-1)*dif_ny + iy.
!
integer, allocatable :: ixi(:), iyi(:)
real(long) :: scale_f
integer :: nx, ny, ix, iy, ixp, iyp, istat, nerrs
integer :: ixdiff, iydiff, num_errors
integer :: naux1, naux2, i, j, factor1, factor2, idum
integer :: ib, jb, il, jl
!
! ip is a support array for pdcft2.
!
integer :: ip(40)
integer :: blk_index
!
! Fourier transform of diffusion coefficient function
nerrs=0
call factor_nodes()
factor1 = 3**pn_fac(2) * 5**pn_fac(3) * 7**pn_fac(4) * &
& 11**pn_fac(5)
!
! Here we are trying to find the smallest number which is evenly
! divisible by the number of processes and is larger than 4*(n+1).
!
factor2 = (4*(dif_nx+1) + factor1 -1)/factor1
nx = minpower2( factor2,idum) * factor1
factor2 = (4*(dif_ny+1) + factor1 -1)/factor1
ny = minpower2( factor2,idum) * factor1
scale_f = 1.d0/ real(nx*ny, long)
!
! Get storage for diffusion array.
!
call initialize_scale(ny, blk_index)
call initialize_carray(df, df_d, df_i, nx, ny, &
& blk_index)
!
! Here, we initialize the local part of the global array df, which
! contains the value of the diffusion coefficient function, evenly
! evaluated between (0, 2*pi). We do a two dimensional Fourier
! transform on the data. Because the size of this array is so small,
! nx by ny, and ultimately we have to transfer the whole array to
! each node, it would probably be more efficient to do the calculation
! locally on each node.
!
! Get the value of the diffusion coefficient function at
! the necessary points.
!
!
! This loop can be simplified considerably. Because blocks of the
! array are column-distributed with the block size equal to the number
! of columns divided by the number of processes, there is only a single
! column block. Also, because the processes are distributed in a 1 x np
! arrangement, the local row index will equal the global row index.
! However, the loop is perfectly general for other process arrangements
! and is correct for this particular case.
!
jl = 0
do jb = 1, df_i%num_col_blks ! loop over the number of column blocks
do j = df_i%scb(jb), df_i%ecb(jb)
! loop over columns in block
! j is a global index
jl = jl + 1 ! jl is local array column index
il = 0
do ib = 1, df_i%num_row_blks ! loop over the number of row blocks
do i = df_i%srb(ib), df_i%erb(ib)
! loop over rows in block
! i is a global index
il = il + 1 ! il is local array row index
df(il,jl) = diff_coef((twopi*(i-1))/nx, &
& (twopi*(j-1))/ny)
enddo
enddo
enddo
enddo
!
! This last loop just determined the diffusion coefficient at evenly
! spaced points along the x and y coordinates.
!
!
!
! Do the Fourier transform.
!
do i= 1, 40
ip(i) = 0
enddo
! Store the array in normal mode overwriting the original array.
ip(1) = 1
ip(2) = 1
!
! Because the size of the 2d Fourier transform is nx by ny, which is much
! smaller than the size of the eigenvalue problem, this could probably
! be done serially on each node more quickly.
!
call pdcft2(df, df, nx, ny, 1,scale_f, sc_icontext, ip)
!
!
! df now has the Fourier coefficients for the diffusion coefficient
! function, which correspond to the D(tilde)(sub ij) given in the
! discussion paper.
!
! Because each process will need most of the Fourier transformed diffusion
! coefficients, it is useful to broadcast all parts of this matrix
! to each process.
!
! First allocate the index arrays.
!
num_errors=0
allocate(ixi(dif_nx*dif_ny), stat=istat)
if( istat .ne. 0 ) num_errors = num_errors + 1
allocate(iyi(dif_nx*dif_ny), stat=istat)
if( istat .ne. 0 ) num_errors = num_errors + 1
! Allocate array for holding global Fourier transform.
allocate(dfg(nx,ny), stat = istat)
if( istat .ne. 0 ) num_errors = num_errors + 1
call igamx2d(sc_icontext,'A',' ',1,1,num_errors,1,-1,-1,-1, &
& -1,-1)
if( num_errors .gt. 0 ) then
if( sc_iam .eq. 0 ) then
write(*,*) 'Error in allocating scratch arrays in ', &
& 'get_diffusion_matrix'
call blacs_abort(sc_icontext, 1)
endif
endif
call clocal_to_rglobal( df, df_d, dfg )
! Here df contains only local portions of the global array, while
! dfg contains the entire global array.
!
!
! Now load up the diffusion operator
! f(ix,iy;ix',iy').
!
! Here we transform the 4d matrix into the 2d matrix where
! i = (iy-1)* dif_nx + ix + 1
! and
! j = (iy'-1)* dif_nx + ix' + 1.
!
! First calculate the index arrays.
!
do ix = 1, dif_nx
do iy = 1, dif_ny
i = (iy-1)* dif_nx + ix
ixi(i) = ix
iyi(i) = iy
enddo
enddo
!
! This final loop loads the matrix elements up for F as given in
! equation 10.
!
jl = 0
do jb = 1, f_i%num_col_blks ! loop over the number of column blocks
do j = f_i%scb(jb), f_i%ecb(jb)
! loop over columns in block
! j is a global index
jl = jl + 1 ! jl is local array column index
iyp = iyi(j)
ixp = ixi(j)
il = 0
do ib = 1, f_i%num_row_blks ! loop over the number of row blocks
do i = f_i%srb(ib), f_i%erb(ib)
! loop over rows in block
! i is a global index
il = il + 1 ! il is local array row index
iy = iyi(i)
ix = ixi(i)
ixdiff = iabs(ix-ixp) + 1
iydiff = iabs(iy-iyp) + 1
f(il,jl) = ( ( ix*ixp + iy*iyp*dif_ly_ratio ) * &
& (dfg(ixdiff, iydiff) - dfg(ix+ixp+1,iy+iyp+1)) &
& + ( ix*ixp - iy*iyp*dif_ly_ratio ) * &
& (dfg(ix+ixp+1,iydiff ) - dfg(ixdiff,iy+iyp+1)))
enddo
enddo
enddo
enddo
deallocate(dfg)
deallocate(ixi)
deallocate(iyi)
!
! We should add routines to free df.
!
return
end subroutine get_diffusion_matrix
!****************************************************************************!
!* *!
!* Module routine expand_temp_profile *!
!* *!
!* Purpose: To obtain the expansion coefficients of the initial *!
!* temperature profile in a sine function expansion *!
!* *!
!****************************************************************************!
subroutine expand_temp_profile(a,a_i,a_d)
!
! Arguments:
! a: real*8,dimension(:,:),(out), local part of the global matrix,
! containing the sine coefficients for initial
! temperature distribution.
! a_d: integer*4, dimension(:),(in), array descriptor for a.
! a_i: g_type, (in), g_type structure for a, see parameter.f.
!
real(long), intent(out) :: a(:,:)
integer, intent(in) :: a_d(DESC_DIM)
type (g_index), intent(in) :: a_i
! Local variables
complex(long), allocatable :: atmp(:,:)
real(long), allocatable :: aux1(:), aux2(:)
integer :: i,j, nx, ny, istat, naux1, naux2, nerrs, jl
integer :: idum, jb, jx, jy
real(long) :: x, y, scale_f
!
! Calculate the minimum power of 2 to hold twice the number of
! Fourier coefficients as sine coefficients. The top half of the
! Fourier coefficients will equal minus the bottom half because
! we are forcing the temperature profile to be odd.
!
nx = minpower2( 2*(dif_nx+1), idum)
ny = minpower2( 2*(dif_ny+1), idum)
scale_f = -twopi / real( nx*ny,long)
nerrs = 0
!
! Temperature profile allocation.
allocate(atmp(nx,ny), stat=istat )
if( istat .ne. 0 ) nerrs = nerrs + 1
!
!
naux1 = 40000 + 2.28*( nx + ny)
naux2 = 20000 + 66*( 256 + 2*max(nx , ny))
!
! Allocate work storage.
allocate(aux1(naux1), stat=istat)
if( istat .ne. 0 ) nerrs = nerrs + 1
allocate(aux2(naux2), stat=istat)
if( istat .ne. 0 ) nerrs = nerrs + 1
!
! Check for allocation errors.
!
call igamx2d(sc_icontext,'A',' ',1,1,nerrs,1,-1,-1,-1,-1,-1)
if( nerrs .gt. 0 ) then
if( sc_iam .eq. 0 ) then
write(*,*) 'Error in allocating scratch arrays in ', &
& 'expand_temp_profile'
call blacs_abort(sc_icontext, 1)
endif
endif
!
!
! Fill atmp with the initial temperatures.
!
! atmp contains the initial temperature profile T(sub 0)(x,y) as used
! in equation 5 in the discussion paper.
!
do i = 1, nx
do j = 1, ny
atmp(i,j) = init_temp((twopi*(i-1))/nx, (twopi*(j-1))/ny)
enddo
enddo
!
! Do the 2d Fourier transform of atmp.
!
! First initialize.
!
! The 2d Fourier transform can be done in parallel, however it
! is such a small part of the problem, it is probably faster to do
! it serially on each node.
!
! Note that we could have used DSINF to obtain these expansion coefficients
! as well.
!
call dcft2(1,atmp,1,nx,atmp,1,nx,nx,ny,1,scale_f ,aux1,naux1, &
& aux2,naux2 )
call dcft2(0,atmp,1,nx,atmp,1,nx,nx,ny,1,scale_f ,aux1,naux1, &
& aux2,naux2 )
!
! The calls to dcft2 calculated the dual Fourier transform as
! defined by equation 5 in the discussion paper.
!
!
! This final loop is to load only those portions of the global array
! corresponding to the local portion of that array for this process.
!
jl = 0
do jb = 1, a_i%num_col_blks ! loop over all column blocks
do j = a_i%scb(jb), a_i%ecb(jb) ! j is global index
jx = mod(j-1, dif_nx) + 2
jy = (j-1) / dif_nx + 2
jl = jl + 1
a(1,jl) = real(atmp(jx,jy),long)
enddo
enddo
deallocate(atmp)
deallocate(aux1)
deallocate(aux2)
return
end subroutine expand_temp_profile
!****************************************************************************!
!* *!
!* Module routine factor_nodes *!
!* *!
!* Purpose: To obtain the powers of prime factorization of the number *!
!* nodes, failing if the factorization is not compatible with *!
!* FFT supported transform lengths *!
!* *!
!****************************************************************************!
subroutine factor_nodes()
! Arguments: None
!
! Local variables
integer n1, n2, l2
!
! Determine the prime factorization of nnodes, which must
! be of the form 2**n * 3**m * 5**i * 7**j * 11**k
! where m cannot be greater than 2 and i, j, and k cannot
! be greater than 1
!
n2 = sc_nnodes
n1 = n2/11
if( n1*11 .eq. n2) then
pn_fac(5) = 1
n2 = n1
endif
n1 = n2/7
if( n1*7 .eq. n2) then
pn_fac(4) = 1
n2 = n1
endif
n1 = n2/5
if( n1*5 .eq. n2) then
pn_fac(3) = 1
n2 = n1
endif
n1 = n2/3
if( n1*3 .eq. n2) then
if ( (n1/3)*3 .eq. n1 ) then
pn_fac(2) = 2
n2 = n1/3
else
pn_fac(2) = 1
n2 = n1
endif
endif
n1 = minpower2(n2,l2)
pn_fac(1) = l2
if( n1 .ne. n2) then
if( sc_iam .eq. 0) then
write(*,*) 'Invalid number of nodes, it must have the form:'
write(*,*) '2**n * 3**m * 5**i * 7**j * 11**k, where '
write(*,*) ' n >= 0, 0<=m<=2 and 0<= i,j,k <=1 '
write(*,*) ' choose a power of 2 for best performance'
call blacs_abort(sc_icontext,1)
endif
endif
end subroutine factor_nodes
!****************************************************************************!
!* *!
!* Module function minpower2 *!
!* *!
!* Purpose: To obtain the smallest number which is a power of 2 and *!
!* greater than or equal to the input argument *!
!* *!
!****************************************************************************!
function minpower2( n, log2n )
!
! Arguments:
! n: integer*4, (in), input number
! log2n: integer*4, (out), log base 2 of the function result
! Function return:
! minpower2: integer*4 (out), smallest number, which is a power of 2
! and greater than or equal to n.
!
integer n, minpower2, log2n
!
! Local variables.
integer m, i
m=n
if( n < 0 ) write(*,*) 'n cannot be negative'
powerloop: do i= 1, bit_size(n)
m = m / 2
if( m .eq. 0 ) exit powerloop
enddo powerloop
if ( 2**(i-1) .ne. n ) then
if( 2**i < 0) write(*,*) 'n too large'
log2n = i
minpower2 = 2**i
else
log2n = i-1
minpower2 = n
endif
return
end function minpower2
end module fourier
module scale
!
! Purpose: To initialize the communications and provide a few
! communication utility routines.
!
! Routines called:
! blacs_abort
! blacs_get
! blacs_gridinfo
! blacs_gridinit
! blacs_pinfo
! dgebr2d
! dgebs2d
! numroc
!
use parameters
implicit none
external numroc
!
! All variables private by default.
!
private
!
! Publicly accessible routines follow.
!
public initialize_scale
public initialize_rarray, initialize_carray
public clocal_to_rglobal, rlocal_to_rglobal
public g_index
!
! Public variables follow.
!
integer, public :: sc_icontext, sc_iam, sc_nnodes
!
! Private variables follow.
!
! MAXBLOCK is the maximum block size. Here it is set to a very
! large number to force an equal noncyclic block distribution
! for the FFTs.
!
!
integer, public, parameter :: MAXBLOCK=50000
integer, public, parameter :: MAX_SC_INDEX=10
integer, public, parameter :: DESC_DIM=9
integer, public, parameter :: DTYPE_=1
integer, public, parameter :: CTXT_=2
integer, public, parameter :: M_=3
integer, public, parameter :: N_=4
integer, public, parameter :: MB_=5
integer, public, parameter :: NB_=6
integer, public, parameter :: RSRC_=7
integer, public, parameter :: CSRC_=8
integer, public, parameter :: LLD_=9
integer :: numroc
integer :: nprow, npcol, myrow, mycol
!
! The block sizes for a given array size are indexed in the
! nblock, mblock and nsize arrays so that, for a given array size,
! the block size calculation is done only once and exactly the same
! block sizes are returned for any particular array size.
!
integer :: nblock(MAX_SC_INDEX), mblock(MAX_SC_INDEX)
integer :: nsize(MAX_SC_INDEX)
!
! The number of different array sizes is limited by the fixed
! dimension of the arrays nblock, mblock and nsize.
!
integer :: icontext, iam, nnodes
integer, save :: sc_indx=0
integer, parameter :: rsrc=0, csrc=0
logical, save :: initialized = .false.
!
! All of the manipulation of the PESSL and SP variables will be
! done in this module and held privately.
!
contains
!****************************************************************************!
!* *!
!* Module routine initialize_scale *!
!* *!
!* Purpose: Initialize blacs and calculate a block size *!
!* *!
!****************************************************************************!
subroutine initialize_scale (n, index)
!
! Arguments:
! n: integer*4 (in), matrix or vector size.
! index: integer*4 (out), index into an array of block sizes.
! Provides a mechanism for creating similar descriptor arrays.
!
!
! This routine assigns the block size based on a given
! n and returns an index, so that multiple arrays can be created with
! compatible block sizes.
!
integer n, index
integer npc, npr, i
if ( .not. initialized ) then
call blacs_pinfo( iam, nnodes )
sc_iam = iam
sc_nnodes = nnodes
!
! Get the number of nodes.
!
!
! The Fourier transform routines require that the processors
! be laid out in a 1 by nnodes arrangement.
!
nprow = 1
npcol = nnodes
call blacs_get(0,0,icontext)
sc_icontext = icontext
call blacs_gridinit( icontext, 'R', nprow, npcol)
sc_icontext = icontext
call blacs_gridinfo( icontext, npr, npc, myrow, mycol)
!
! Check that the system is gridded as expected.
!
if( npr .ne. nprow .or. npc .ne. npcol) then
if( iam .eq. 0) then
write(*,*) 'number of processor rows and columns'
write(*,*) 'incorrect ', nprow, npr, npcol, npc
call blacs_abort(icontext,1)
endif
endif
initialized = .true.
endif
!
! If we have already calculated a block size based on estimated
! array size, return the index for that block size.
!
do i = 1, sc_indx
if( n .eq. nsize(i)) then
index = i
return
endif
enddo
!
! Compute a block size.
!
sc_indx = sc_indx + 1
if ( sc_indx .GT. MAX_SC_INDEX ) then
if( iam .eq. 0 ) then
write(*,*) 'Used more than the maximum number of '
write(*,*) 'indices in initialize_scale, Maximum is ', &
& MAX_SC_INDEX
call blacs_abort(icontext,1)
endif
endif
index = sc_indx
nsize(index) = n
!
! Always choose a square block with a maximum dimension of MAXBLOCK.
!
if( ( n ) / nnodes .gt. MAXBLOCK ) then
mblock(index) = MAXBLOCK
else
mblock(index) = (n ) / nnodes
endif
if( mblock(index) .lt. 1 ) then
if( iam .eq. 0 ) then
write(*,*) 'problem size too small for number of nodes'
write(*,*) 'try increasing the nx and ny'
write(*,*) n, nnodes
call blacs_abort(sc_icontext, 1)
endif
endif
nblock(index) = mblock(index)
return
end subroutine initialize_scale
!
! This routine is provided to allocate dynamically the space
! needed for the local part of a global array and initialize the
! associated array descriptor. It also returns array-useful
! indices to do local to global index conversion.
!
! initialize_rarray => real array initialization.
! initialize_carray => complex array initialization.
!
!****************************************************************************!
!* *!
!* Module routine initialize_rarray *!
!* *!
!* Purpose: Allocate space for a real array and create associated *!
!* descriptor array and index array *!
!* *!
!****************************************************************************!
subroutine initialize_rarray( array, desc_array, &
& index_array, m, n, blk_index)
!
! Arguments:
! array: pointer to real*8 (out), pointer to real array, initialized.
! desc_array: integer*4 (out), empty descriptor array, initialized.
! index_array: g_index (out), pointer to g_index structure,
! see parameter.f, initialized.
! m: integer*4 (out), scalar number of rows in global array.
! n: integer*4 (out), scalar number of columns in global array.
! blk_index: integer*4 (in), index into array of block sizes to use
! for initializing the descriptor array.
!
integer, intent(out) :: desc_array(DESC_DIM)
integer, intent(in) :: m, n, blk_index
type (g_index), pointer :: index_array
real(long), pointer :: array(:,:)
! Local variables
integer :: irows, icols, istat, i, j
integer :: start_row_block, start_col_block
integer :: mb, nb, num_mb, num_nb
!
! Check to see if the block sizes were already calculated.
!
if ( blk_index .lt.1 .or. blk_index .gt. sc_indx ) then
if( iam .eq. 0 ) then
write(*,*) 'No initialization done for index ', blk_index
call blacs_abort(icontext, 1)
endif
endif
mb = mblock(blk_index)
nb = nblock(blk_index)
irows = numroc( m, mb, myrow, rsrc, nprow )
icols = numroc( n, nb, mycol, csrc, npcol )
allocate(array(max(irows,1),max(icols,1)), stat=istat)
if ( istat .ne. 0) then
write(*,*) 'allocate failed in initialize_array'
call blacs_abort(icontext,1)
endif
!
! Calculate the number of row and column blocks.
!
num_mb = ( (irows + mb -1)/ mb )
num_nb = ( (icols + nb -1)/ nb )
allocate (index_array)
index_array%num_row_blks = num_mb
index_array%num_col_blks = num_nb
allocate(index_array%srb(num_mb))
allocate(index_array%erb(num_mb))
allocate(index_array%scb(num_nb))
allocate(index_array%ecb(num_nb))
desc_array(DTYPE_) = 1
desc_array(M_) = m
desc_array(N_) = n
desc_array(MB_) = mb
desc_array(NB_) = nb
desc_array(RSRC_) = rsrc
desc_array(CSRC_) = csrc
desc_array(CTXT_) = icontext
desc_array(LLD_) = max(irows,1)
!
start_row_block = mod( nprow + myrow - rsrc , nprow )
start_col_block = mod( npcol + mycol - csrc , npcol )
do i = 1, index_array%num_row_blks
index_array%srb(i) = (start_row_block + (i - 1)*nprow) * &
& mb+1
index_array%erb(i) = index_array%srb(i) + mb - 1
enddo
index_array%erb(num_mb) = mod(irows-1,mb) + &
& index_array%srb(num_mb)
do i = 1, index_array%num_col_blks
index_array%scb(i) = (start_col_block + (i - 1)*npcol) * &
& nb + 1
index_array%ecb(i) = index_array%scb(i) + nb - 1
enddo
index_array%ecb(num_nb) = mod(icols-1,nb) + &
& index_array%scb(num_nb)
end subroutine initialize_rarray
! Complex array initialization.
!
!****************************************************************************!
!* *!
!* Module routine initialize_carray *!
!* *!
!* Purpose: Allocate space for a complex array and create associated *!
!* descriptor array and index array *!
!* *!
!****************************************************************************!
subroutine initialize_carray( array, desc_array, &
& index_array, m, n, blk_index)
!
! Arguments:
! array: pointer to complex (out), pointer to real array, initialized.
! desc_array: integer*4 (out), empty descriptor array, initialized.
! index_array: g_index (out), pointer to g_index structure,
! see parameter.f, initialized.
! m: integer*4 (out), scalar number of rows in global array.
! n: integer*4 (out), scalar number of columns in global array.
! blk_index: integer*4 (in), index into array of block sizes to use
! for initializing the descriptor array.
!
integer desc_array(DESC_DIM), m, n, blk_index
type (g_index),pointer :: index_array
complex(long), pointer :: array(:,:)
! Local variables
integer :: irows, icols, istat, i, j
integer :: start_row_block, start_col_block
integer :: mb, nb, num_mb, num_nb
!
! Check to see if the block sizes were already calculated.
!
if ( blk_index .lt.1 .or. blk_index .gt. sc_indx ) then
if( iam .eq. 0 ) then
write(*,*) 'No initialization done for index ', blk_index
call blacs_abort(icontext, 1)
endif
endif
mb = mblock(blk_index)
nb = nblock(blk_index)
irows = numroc( m, mb, myrow, rsrc, nprow )
icols = numroc( n, nb, mycol, csrc, npcol )
allocate(array(max(irows,1),max(icols,1)), stat=istat)
if ( istat .ne. 0) then
write(*,*) 'allocate failed in initialize_array'
call blacs_abort(icontext,1)
endif
!
! Calculate the number of row and column blocks.
!
num_mb = ( (irows + mb -1)/ mb )
num_nb = ( (icols + nb -1)/ nb )
allocate(index_array, stat=istat)
if ( istat .ne. 0) then
write(*,*) 'allocate failed in initialize_array'
call blacs_abort(icontext,1)
endif
index_array%num_row_blks = num_mb
index_array%num_col_blks = num_nb
allocate(index_array%srb(num_mb))
allocate(index_array%erb(num_mb))
allocate(index_array%scb(num_nb))
allocate(index_array%ecb(num_nb))
desc_array(DTYPE_) = 1
desc_array(M_) = m
desc_array(N_) = n
desc_array(MB_) = mb
desc_array(NB_) = nb
desc_array(RSRC_) = rsrc
desc_array(CSRC_) = csrc
desc_array(CTXT_) = icontext
desc_array(LLD_) = max(irows,1)
!
start_row_block = mod( nprow + myrow - rsrc , nprow )
start_col_block = mod( npcol + mycol - csrc , npcol )
do i = 1, index_array%num_row_blks
index_array%srb(i) = (start_row_block + (i - 1)*nprow) * &
& mb+1
index_array%erb(i) = index_array%srb(i) + mb - 1
enddo
index_array%erb(num_mb) = mod(irows-1,mb) + &
& index_array%srb(num_mb)
do i = 1, index_array%num_col_blks
index_array%scb(i) = (start_col_block + (i - 1)*npcol) * &
& nb + 1
index_array%ecb(i) = index_array%scb(i) + nb - 1
enddo
index_array%ecb(num_nb) = mod(icols-1,nb) + &
& index_array%scb(num_nb)
end subroutine initialize_carray
!
!****************************************************************************!
!* *!
!* Module routine clocal_to_rglobal *!
!* *!
!* Purpose: Take the real parts of the local portions of a complex matrix *!
!* and distribute them globally to each node *!
!* *!
!****************************************************************************!
subroutine clocal_to_rglobal(a,a_d,a_glob)
!
! Arguments:
! a: complex*16, dimension(:,:), is the local part of a
! global complex array.
! a_d: integer*4, array descriptor for a.
! a_glob: real*8, dimension(:,:), entire matrix A on each node.
!
complex(long), intent(in) :: a(:,:)
integer, intent(in) :: a_d(DESC_DIM)
real(long), intent(out) :: a_glob(:,:)
!
! Local variables.
!
integer :: nrow_blks, ncol_blks, ib, jb, ibl, jbl, i, j
integer :: m, n, nb, mb, ig, jg, lda, il, jl, prow, pcol
integer :: iarow, iacol, ni, nj
!
! m is number of rows in global matrix.
! n is number of columns in global matrix.
! mb and nb are rows and columns in each block.
! prow and pcol are the processor row and column containing a block.
! ib, jb, ibl, jbl are global and local block indices.
! il, jl, ig, jg are local and global matrix indices.
!
!
!
! Start of executable code.
!
!====================================================================
!
! Determine the total number of row and column blocks.
m = a_d(M_)
n = a_d(N_)
mb = a_d(MB_)
nb = a_d(NB_)
iarow = a_d(RSRC_)
iacol = a_d(CSRC_)
nrow_blks = ( m + mb -1 )/ mb
ncol_blks = ( n + nb - 1 )/ nb
!
! Determine leading dimension of global array.
lda = size(a_glob, dim=1)
!
! Loop over all of the blocks.
!
do jb = 0, ncol_blks - 1
!
! Loop over column blocks, determining both local and global j indices.
jg = jb * nb + 1
nj = nb
if (jb .eq. ncol_blks - 1) nj = mod( n - 1, nb) + 1
jbl = ( jb + iacol ) / npcol - (mycol + iacol) / npcol
jl = jbl * nb + 1
pcol = mod((jb + iacol), npcol )
do ib = 0, nrow_blks - 1
!
! Loop over row blocks, determining both local and global i indices.
ig = ib * mb + 1
ni = mb
if (ib .eq. nrow_blks - 1) ni = mod( m - 1, mb) + 1
ibl = ( ib + iarow ) / nprow - (myrow + iarow) /nprow
il = ibl * mb + 1
prow = mod((ib + iarow), nprow )
!
! Determine if this block is on my processor.
!
if( prow .eq. myrow .and. pcol .eq. mycol) then
!
! Block is on my processor.
!
! using Fortran 90 array language this is
! a_glob(ig:ig+ni-1,jg:jg+nj-1) = a(il:il+ni-1:jl+nj-1)
!
do j = 1, nj
do i = 1, ni
a_glob( ig+i-1, jg+j-1 ) = a( il+i-1, jl+j-1)
enddo
enddo
call dgebs2d(icontext,'ALL',' ',ni,nj,a_glob(ig,jg),lda)
else
!
! Block is on somebody elses processor.
!
call dgebr2d(icontext,'ALL',' ',ni,nj,a_glob(ig,jg), &
& lda, prow, pcol)
endif
enddo
enddo
return
end subroutine clocal_to_rglobal
!****************************************************************************!
!* *!
!* Module routine rlocal_to_rglobal *!
!* *!
!* Purpose: Take the local portions of a real matrix *!
!* and distribute them globally to each node *!
!* *!
!****************************************************************************!
subroutine rlocal_to_rglobal(a,a_d,a_glob)
!
! Arguments:
! a: real*8, dimension(:,:), is the local part of a global real array.
! a_d: integer*4, array descriptor for a.
! a_glob: real*8, dimension(:,:), entire matrix A on each node.
!
! Input arguments.
!
real(long), intent(in) :: a(:,:)
integer, intent(in) :: a_d(DESC_DIM)
real(long), intent(out) :: a_glob(:,:)
!
! Local variables.
!
integer :: nrow_blks, ncol_blks, ib, jb, ibl, jbl, i, j
integer :: m, n, nb, mb, ig, jg, lda, il, jl, prow, pcol
integer :: iarow, iacol, ni, nj
!
! m is number of rows in global matrix.
! n is number of columns in global matrix.
! mb and nb are rows and columns in each block.
! prow and pcol are the processor row and column containing a block.
! ib, jb, ibl, jbl are global and local block indices.
! il, jl, ig, jg are local and global matrix indices.
!
!
!
! Start of executable code.
!
!====================================================================
!
! Determine the total number of row and column blocks.
m = a_d(M_)
n = a_d(N_)
mb = a_d(MB_)
nb = a_d(NB_)
iarow = a_d(RSRC_)
iacol = a_d(CSRC_)
nrow_blks = ( m + mb -1 )/ mb
ncol_blks = ( n + nb - 1 )/ nb
!
! Determine leading dimension of global array.
lda = size(a_glob, dim=1)
!
! Loop over all of the blocks.
!
do jb = 0, ncol_blks - 1
!
! Loop over column blocks, determining both local and global j indices
jg = jb * nb + 1
nj = nb
if (jb .eq. ncol_blks - 1) nj = mod( n - 1, nb) + 1
jbl = ( jb + iacol ) / npcol - (mycol + iacol) / npcol
jl = jbl * nb + 1
pcol = mod((jb + iacol), npcol )
do ib = 0, nrow_blks - 1
!
! Loop over row blocks, determining both local and global i indices.
ig = ib * mb + 1
ni = mb
if (ib .eq. nrow_blks - 1) ni = mod( m - 1, mb) + 1
ibl = ( ib + iarow ) / nprow - (myrow + iarow) /nprow
il = ibl * mb + 1
prow = mod((ib + iarow), nprow )
!
! Determine if this block is on my processor.
!
if( prow .eq. myrow .and. pcol .eq. mycol) then
!
! Block is on my processor.
!
do j = 1, nj
do i = 1, ni
a_glob( ig+i-1, jg+j-1 ) = a( il+i-1, jl+j-1)
enddo
enddo
call dgebs2d(icontext,'ALL',' ',ni,nj,a_glob(ig,jg),lda)
else
!
! Block is on somebody elses processor.
!
call dgebr2d(icontext,'ALL',' ',ni,nj,a_glob(ig,jg), &
& lda, prow, pcol)
endif
enddo
enddo
return
end subroutine rlocal_to_rglobal
end module scale
program main
!
! Purpose, to find the cooling rate for a specified set of
! points in an anisotropic rectangular beam, immersed in a constant
! heat bath with a temperature of 0.
!
! Routines called:
! expand_temp_profile
! get_diffusion_matrix
!
use parameters
use diffusion
use fourier
use pessl_hpf
implicit none
integer :: n, ix, jx, iy, jy, k, i, j, stat, it, ij
integer :: num_errors
!
! a contains the sine expansion coefficients of the initial
! temperature profile.
! b contains the eigenvectors of the diffusion operator in the
! sine function basis.
! ab contains the initial temperature profile expanded in the
! eigenvectors of the diffusion operator.
! f contains the matrix elements of the diffusion operation in
! sine function basis.
! lambda contains the eigenvalues of the diffusion operator.
!
! df contains the Fourier transform of the diffusion coefficient function.
!
real(long) :: t1, t2, delx, dely
integer :: j1, j2
real(long), allocatable :: dif_x(:), dif_y(:)
real(long), allocatable :: lambda(:)
real(long), allocatable :: gap(:)
real(long), allocatable :: f(:,:), b(:,:), a(:), a_rep(:)
real(long), allocatable :: x(:,:), ab(:), abt(:,:)
real(long), allocatable :: xsines(:,:), ysines(:,:), temp(:,:)
integer :: biga_index, num_eigvalues, num_vectors
! HPF directives, we will only use descriptive mapping except in main
!HPF$ DISTRIBUTE (*,BLOCK) :: f, b, x, abt, temp
!HPF$ DISTRIBUTE (BLOCK) :: a, ab
! lambda is a replicated array.
!
! Read in the problem size, initialize the problem dimensions,
! choose functional form for the spatially dependent heat diffusion
! coefficients, choose functional form of initial temperature distribution
! and choose the number of points, in both space and time, of the solution
! to print out.
!
call init_diffusion
allocate( dif_x(dif_numx*dif_numy) )
allocate( dif_y(dif_numy*dif_numx) )
!
! Assign a simple linear array of points.
!
delx = PI/ ( dif_numx + 1.d0)
dely = PI/ ( dif_numy + 1.d0)
do i = 1, dif_numx
do j = 1, dif_numy
ij = dif_numx*(j-1) + i
dif_x(ij) = delx* i
dif_y(ij) = dely * j
enddo
enddo
num_errors = 0
!
! Read in how many sine functions to include in both the
! x and y directions.
!
! Because we need to get the Fourier coefficients of the sums
! and differences of the indices, we need to include twice as
! many Fourier coefficients as the number of sine expansion coefficients.
! Also, because the top and bottom halves of the Fourier
! transform are identical,
! an artifact of artificially extending the diffusion coefficient
! function and the initial temperature distribution, we need to
! double the number of Fourier coefficients again. Finally, the
! extra sum of one comes from the fact that the sine function
! expansion starts a 1 and the Fourier expansion starts at 0.
!
! n is the order of the diffusion operator equation.
n = dif_nx * dif_ny
!
!
! Allocate room for the eigenvalues of diffusion operator.
!
allocate( lambda(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
allocate( a(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
allocate( ab(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
allocate( a_rep(n), stat=stat)
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for sines of x and y coordinates.
!
allocate( xsines(dif_npts, dif_nx) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( ysines(dif_npts, dif_ny) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for temperature history at selected points.
!
allocate( temp(dif_npts, dif_ntemps) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( f(n,n) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( b(n,n) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( abt(n,dif_ntemps) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
allocate( x(n,dif_ntemps) , stat=stat )
if( stat .ne. 0) num_errors = num_errors + 1
!
! Allocate room for global temperature profile expansion vector at time t.
!
if( num_errors .gt. 0 ) then
write(*,*) 'Error in allocating arrays in main'
stop
endif
!
! A call to expand_temp_profile returns the sine expansion
! coefficients of the initial temperature profile.
!
!
!
! Represent initial temperature in sine function expansion.
!
call expand_temp_profile(a)
a_rep = a
!
! Here, we are calculating the initial set of coefficients
! in the sine function expansion as given in equations 3 and 4 of
! the discussion paper
!
!
! The call to get_diffusion_matrix returns the diffusion
! operator in the sine function basis.
!
call get_diffusion_matrix(f)
!
! This last call determines the matrix elements defined by equation 10
! in the discussion paper.
!
!
! Here we precalculate the sine functions, sin(kx) and sin(jy) used
! in equation 13 of the discussion paper.
! These sine functions are only evaluated at the points x and y for
! which the solution is evaluated.
!
do i = 1, dif_nx
do j = 1, dif_npts
t1 = i*dif_x(j)
xsines(j,i) = sqrt(2.d0/pi) * dsin(t1)
enddo
enddo
do i = 1, dif_ny
do j = 1, dif_npts
t2 = i*dif_y(j)
ysines(j,i) = sqrt(2.d0/pi) * dsin( t2)
enddo
enddo
!
! Test to see if we had any allocation errors.
!
if( num_errors .gt. 0 ) then
write(*,*) 'Error in allocating arrays for syevx in main'
stop
endif
!
! The call to syevx will find both the eigenvalues and eigenvectors
! of the diffusion matrix operator f. The eigenvalues will be stored in
! the vector lambda and the corresponding eigenvectors will be stored in
! the matrix b. The f and b matrices in the program correspond to the
! F and B matrices in equations 11 and 12 in the
! discussion paper.
!
!
call syevx(f,lambda,'u', z=b)
!
! Multiply the transpose of the eigenvector matrix, b, with the sine
! expansion of the initial temperature profile, a, to obtain the
! initial temperature profile in terms of the eigenfuctions of the
! diffusion operator.
!
ab(i) = 0.d0
do i = 1, n
do j = 1, n
ab(i) = b(j,i)*a_rep(j) + ab(i)
enddo
enddo
!
! This first matrix multiplication, yielding the matrix ab,
! corresponds to the inner summation in equation 10
! of the discussion paper.
!
!
! Calculate temperature profile for each time step.
!
do it = 1, dif_ntemps
i = 0
do i = 1, n
abt(i,it) = exp( -lambda(i) *(it-1)*dif_delta_t) * ab(i)
enddo
enddo
!
! abt now has the expansion of the temperature profile in terms of the
! eigenvectors of the diffusion operator.
!
!
! Multiply the eigenvector matrix with abt to give the sine function
! expansion of the temperature profile at time t, x.
!
call gemm(1.d0,b,abt,0.d0,x,'N','N')
! This last sum corresponds to the outer sum of equation 12, where the
! time dependent expansion coefficients a{sub l}(t) are stored in the
! temporary array x in the program.
!
do it = 1, dif_ntemps
do k = 1, dif_npts
temp(k, it) = 0.d0
enddo
enddo
do it = 1, dif_ntemps
do i = 1, dif_npts
iy = (i-1)/dif_nx+1
ix = mod(i-1,dif_nx)+1
do k = 1, dif_npts
temp(k,it) = temp(k,it) + xsines(k,ix) * ysines(k,iy) &
& * x(i,it)
enddo
enddo
enddo
!
! This last do loop corresponds to the double summation in equation
! 13 of the discussion paper.
!
!
! Here, we are just writing out the temperatures at the selected times
! and points.
!
write(*,*) ' point # X Y'
do i = 1, dif_npts
write(*,'(2x, i6, 2x, 2f11.4)') i, dif_x(i), dif_y(i)
enddo
write(*,*)
do k = 1, dif_npts, 6
write(*,*)
write(*,'(30X,'Points'')')
write(*,'('' TIME '',6(5x,''#'', i4))') (i, i=k, k+5)
do i = 1, dif_ntemps
write(*,'(7f10.5)') i*dif_delta_t, &
& (temp(j,i),j=k,min(k+5,dif_npts))
enddo
enddo
deallocate(xsines)
deallocate(ysines)
deallocate(lambda)
deallocate(temp)
deallocate(a)
deallocate(abt)
deallocate(a)
deallocate(f)
deallocate(dif_x)
deallocate(dif_y)
stop
end
module parameters
!
! Purpose: Define system wide parameters and pessl structure.
!
implicit none
public
integer, parameter :: long=8, short=4
real(long), parameter :: pi = 3.141592653589793d0
real(long), parameter :: twopi = 2.d0*pi
end module parameters
module diffusion
!
! Purpose: Assign problem parameters and initial data.
!
! Routines called:
! none
!
use parameters
implicit none
private
!
! Make all entities private by default.
! Have all public entities have the prefix dif_.
!
! The following are the publicly available routines.
!
public init_diffusion, init_temp, diff_coef
!
! The following are publicly available variables.
!
real, public :: dif_ly_ratio
integer, public :: dif_nx, dif_ny, dif_npts, dif_ntemps
integer, public :: dif_numx, dif_numy
real(long), public :: dif_delta_t
!
! dif_ly_ratio is the ratio of the x and y lengths of the beam.
! dif_nx is the number of sine expansion coefficients to use
! in the x direction.
! dif_ny is the number of sine expansion coefficients to use
! in the y direction.
! dif_delta_t is the size of the time step to be display on output.
! dif_ntemps is the total number of temperatures to display per point.
! dif_npts is the total number of points to output.
!
!
!
! Private variables
!
integer :: init_f=1, diff_f=1
! init_f chooses the functional form of initial distribution of temperature.
! diff_f chooses the functional form for spatially dependent head diffusion
! coefficient.
contains
!****************************************************************************!
!* *!
!* Module routine init_diffusion *!
!* *!
!* Purpose: Initialize problem size, number of output point and *!
!* functional form of diffusion constant and initial temperature *!
!* distribution *!
!* *!
!****************************************************************************!
subroutine init_diffusion
namelist /input/ ly_ratio, delta_t, numx, numy, nx, ny, numt, &
& init_f, diff_f
integer :: numx=5, numy=5, nx=7, ny=7, numt=20
real(long) :: ly_ratio=1.d0, delta_t=0.1
real(long) :: delx, dely
integer :: i, j, ij
logical :: ex
!==============================================================================!
! Start of executable code !
inquire ( file='diffus.naml', exist=ex)
if( ex ) then
open( 10, file='diffus.naml', action='read')
read( 10, input)
close(10)
endif
dif_ly_ratio = ly_ratio
dif_npts = numx*numy
dif_delta_t = delta_t
dif_ntemps = numt
dif_nx = nx
dif_ny = ny
dif_numx = numx
dif_numy = numy
return
end subroutine init_diffusion
!****************************************************************************!
!* *!
!* Module routine init_temp *!
!* *!
!* Purpose: Return the initial temperature of the bar at a particular *!
!* point *!
!* *!
!****************************************************************************!
function init_temp(x, y)
!
! Arguments:
! x: real*8 (in), x coordinate
! y: real*8 (in), y coordinate
! Function return:
! init_temp: real*8 (out), initial temperature at (x,y)
!
real(long), intent(in) :: x, y
real(long) :: init_temp
!
! The problem has been scaled to go from 0 to pi in both the x
! and y directions. To calculate the expansion coefficients, we
! define the function to be odd about pi and use the range 0 < x < 2*pi
!
! Local variables.
integer :: isign
real(long) :: x1, y1
!
isign = 1
x1 = x
if( x .gt. pi ) then
isign = -isign
x1 = twopi - x
endif
y1 = y
if( y .gt. pi ) then
isign = -isign
y1 = twopi - y
endif
!
! Choose very simple temperature profile cases.
!
select case (init_f)
case (1)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)
case (2)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*y1
case (3)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*x1
case (4)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)*x1*y1
case (5)
init_temp = isign*(x1*(pi-x1))*y1*(pi-y1)
case (6)
init_temp = isign*(x1*(pi-x1))**2 *y1*(pi-y1)
case (7)
init_temp = isign*(x1*(pi-x1))*(y1*(pi-y1))**2
case default
init_temp = isign*sin(x1)*sin(y1)
end select
return
end function init_temp
!****************************************************************************!
!* *!
!* Module routine diff_coef *!
!* *!
!* Purpose: Return the value of the thermal diffusion coefficient at *!
!* an arbitrary point *!
!* *!
!****************************************************************************!
function diff_coef(x, y)
! Arguments:
! x: real*8 (in), x coordinate
! y: real*8 (in), y coordinate
! Function return:
! diff_coef: real*8 (out), diffusion coefficient at (x,y)
!
real(long), intent(in) :: x, y
real(long) :: diff_coef
!
! The problem has been scaled to go from 0 to pi in both the x
! and y directions. To simplify the matrix element calculations,
! we define the function to be even about pi.
!
! Local variables.
real(long) :: x1, y1
!==============================================================================!
! Start of executable code. !
x1 = x
if( x .gt. pi ) x1 = twopi - x
y1 = y
if( y .gt. pi ) y1 = twopi - y
!
! Choose very simple diffusion coefficient cases.
!
select case (diff_f)
case (1)
diff_coef = .5d0 + (x1 + y1) / (2 * twopi)
case (2)
diff_coef = ((1.d0 + x1)*(pi - x1 + 1.d0)*(y1 + pi))/ 3*pi
case (3)
diff_coef = (y1 + pi) * pi/((pi + x1) * (2* pi - x1))
case default
diff_coef = 1.d0
end select
return
end function diff_coef
end module diffusion
module fourier
!
! Purpose: To represent both the diffusion operator and
! the temperature profile in a sine function basis.
!
! Routines called:
! fft
!
use parameters
use diffusion
use pessl_hpf
use hpf_library
implicit none
private
!
! all entities private by default
!
!
! publicly available routines
!
public expand_temp_profile, get_diffusion_matrix
!
! publicly available variables
!
!
! private variables
!
! integer :: pn_fac(5) = 5*0 ! prime factors of number of nodes
! nnodes = 2**pn_fac(1) * 3**pn_fac(2) * 5**pn_fac(3) *
! 7**pn_fac(4) * 11**pn_fac(5)
!
! private routines
!
private minpower2, factor_nodes
contains
!****************************************************************************!
!* *!
!* Module routine get_diffusion_matrix *!
!* *!
!* Purpose: To obtain the matrix representation of the diffusion *!
!* operator in a sine function basis *!
!* *!
!****************************************************************************!
subroutine get_diffusion_matrix(f)
!
! Arguments:
! f: real*8,dimension(:,:),(out), local part of the global matrix
! containing the diffusion operator in sine function basis.
!
real(long), intent(out) :: f(:,:)
!HPF$ DISTRIBUTE *(*,BLOCK) :: f
! Local variables
!
! df contains the diffusion coefficient before the call to fft.
! df contains the Fourier transpose of diffusion coefficients after the call.
!
complex(long), allocatable :: df(:,:)
!HPF$ DISTRIBUTE (*,BLOCK) :: df
!
! ixi and iyi are arrays which, given a global index,
! return the x and y offsets. Recall that the large arrays
! are 4 dimensional arrays collapsed into 2 dimensions,
! where i = (ix-1)*dif_ny + iy.
!
integer, allocatable :: ixi(:), iyi(:)
real(long) :: scale_f
integer :: nx, ny, ix, iy, ixp, iyp, istat
integer :: ixdiff, iydiff, num_errors
integer :: naux1, naux2, i, j, factor1, factor2, idum
integer :: pn_fac(5) ! prime factors of number of nodes
!
! Fourier transform of diffusion coefficient function
pn_fac = 0
call factor_nodes(pn_fac)
factor1 = 3**pn_fac(2) * 5**pn_fac(3) * 7**pn_fac(4) * &
& 11**pn_fac(5)
!
! Here we are trying to find the smallest number which is evenly
! divisible by the number of processes and is larger than 4*(n+1).
!
factor2 = (4*(dif_nx+1) + factor1 -1)/factor1
nx = minpower2( factor2,idum) * factor1
factor2 = (4*(dif_ny+1) + factor1 -1)/factor1
ny = minpower2( factor2,idum) * factor1
scale_f = 1.d0/ real(nx*ny, long)
!
! Get storage for diffusion array.
!
allocate(df(nx,ny))
!
! Here, we initialize the local part of the global array df, which
! contains the value of the diffusion coefficient function, evenly
! evaluated between (0, 2*pi). We do a two dimensional Fourier
! transform on the data. Because the size of this array is so small,
! nx by ny, and ultimately we have to transfer the whole array to
! each node, it would probably be more efficient to do the calculation
! locally on each node.
!
! Get the value of the diffusion coefficient function at
! the necessary points.
!
do j = 1, ny
do i =1, nx
df(i,j) = diff_coef((twopi*(i-1))/nx,(twopi*(j-1))/ny)
enddo
enddo
!
! This last loop just determined the diffusion coefficient at evenly
! spaced points along the x and y coordinates.
!
!
!
! Do the Fourier transform.
!
call fft(df,scale=scale_f,transpose='N')
!
!
! df now has the Fourier coefficients for the diffusion coefficient
! function, which correspond to the D(tilde)(sub ij) given in the
! discussion paper.
!
!
! First allocate the index arrays.
!
num_errors=0
allocate(ixi(dif_nx*dif_ny), stat=istat)
if( istat .ne. 0 ) num_errors = num_errors + 1
allocate(iyi(dif_nx*dif_ny), stat=istat)
if( istat .ne. 0 ) num_errors = num_errors + 1
!
! Now load up the diffusion operator
! f(ix,iy;ix',iy').
!
! Here we transform the 4d matrix into the 2d matrix where
! i = (iy-1)* dif_nx + ix + 1
! and
! j = (iy'-1)* dif_nx + ix' + 1.
!
! First calculate the index arrays.
!
do ix = 1, dif_nx
do iy = 1, dif_ny
i = (iy-1)* dif_nx + ix
ixi(i) = ix
iyi(i) = iy
enddo
enddo
!
! This final loop loads the matrix elements up for F as given in
! equation 10.
!
do j = 1, dif_nx*dif_ny
iyp = iyi(j)
ixp = ixi(j)
do i = 1, dif_nx*dif_ny
iy = iyi(i)
ix = ixi(i)
ixdiff = iabs(ix-ixp) + 1
iydiff = iabs(iy-iyp) + 1
f(i,j) = ( ( ix*ixp + iy*iyp*dif_ly_ratio ) * &
& real(df(ixdiff, iydiff) - df(ix+ixp+1,iy+iyp+1)) &
& + ( ix*ixp - iy*iyp*dif_ly_ratio ) * &
& real(df(ix+ixp+1,iydiff ) - df(ixdiff,iy+iyp+1)))
enddo
enddo
deallocate(df)
deallocate(ixi)
deallocate(iyi)
return
end subroutine get_diffusion_matrix
!****************************************************************************!
!* *!
!* Module routine expand_temp_profile *!
!* *!
!* Purpose: To obtain the expansion coefficients of the initial *!
!* temperature profile in a sine function expansion *!
!* *!
!****************************************************************************!
subroutine expand_temp_profile(a)
!
! Arguments:
! a: real*8,dimension(:),(out), local part of the global matrix,
! containing the sine coefficients for initial
! temperature distribution.
!
real(long), intent(out) :: a(:)
!HPF$ DISTRIBUTE *(BLOCK) :: a
! Local variables
complex(long), allocatable :: atmp(:,:)
!HPF$ DISTRIBUTE (*,BLOCK) :: atmp
integer :: i,j, nx, ny, istat, naux1, naux2
integer :: idum, jb, jx, jy
real(long) :: x, y, scale_f
!
! Calculate the minimum power of 2 to hold twice the number of
! Fourier coefficients as sine coefficients. The top half of the
! Fourier coefficients will equal minus the bottom half because
! we are forcing the temperature profile to be odd.
!
nx = minpower2( 2*(dif_nx+1), idum)
ny = minpower2( 2*(dif_ny+1), idum)
scale_f = -twopi / real( nx*ny,long)
!
! Temperature profile allocation.
allocate(atmp(nx,ny), stat=istat )
if( istat .ne. 0 ) then
write(*,*) 'allocation failure in expand_temp_profile'
stop
endif
!
!
do i = 1, nx
do j = 1, ny
atmp(i,j) = init_temp((twopi*(i-1))/nx, (twopi*(j-1))/ny)
enddo
enddo
!
! Do the 2d Fourier transform of atmp.
!
call fft(atmp,scale=scale_f,transpose='N')
!
! The calls to fft calculated the dual Fourier transform as
! defined by equation 5 in the discussion paper.
!
!
! This final loop is to load only those portions of the global array
! corresponding to the local portion of that array for this processor.
!
do j = 1, dif_nx * dif_ny
jx = mod(j-1, dif_nx) + 2
jy = (j-1) / dif_nx + 2
a(j) = real(atmp(jx,jy),long)
enddo
deallocate(atmp)
return
end subroutine expand_temp_profile
!****************************************************************************!
!* *!
!* Module routine factor_nodes *!
!* *!
!* Purpose: To obtain the powers of prime factorization of the number *!
!* nodes, failing if the factorization is not compatible with *!
!* FFT supported transform lengths *!
!* *!
!****************************************************************************!
subroutine factor_nodes(pn_fac)
! Arguments:
integer :: pn_fac(:)
!
! Local variables
integer n1, n2, l2
!
! Determine the prime factorization of nnodes, which must
! be of the form 2**n * 3**m * 5**i * 7**j * 11**k
! where 0 <= m <=2, 0 <= i <= 1, 0 <= j <= 1, 0 <= k <= 1,
! and 0> n >= 25.
!
n2 = number_of_processors()
n1 = n2/11
if( n1*11 .eq. n2) then
pn_fac(5) = 1
n2 = n1
endif
n1 = n2/7
if( n1*7 .eq. n2) then
pn_fac(4) = 1
n2 = n1
endif
n1 = n2/5
if( n1*5 .eq. n2) then
pn_fac(3) = 1
n2 = n1
endif
n1 = n2/3
if( n1*3 .eq. n2) then
if ( (n1/3)*3 .eq. n1 ) then
pn_fac(2) = 2
n2 = n1/3
else
pn_fac(2) = 1
n2 = n1
endif
endif
n1 = minpower2(n2,l2)
pn_fac(1) = l2
if( n1 .ne. n2) then
write(*,*) 'Invalid number of nodes, it must have the form:'
write(*,*) '2**n * 3**m * 5**i * 7**j * 11**k, where '
write(*,*) ' n >= 0, 0<=m<=2 and 0<= i,j,k <=1 '
write(*,*) ' choose a power of 2 for best performance'
stop
endif
end subroutine factor_nodes
!****************************************************************************!
!* *!
!* Module function minpower2 *!
!* *!
!* Purpose: To obtain the smallest number which is a power of 2 and *!
!* greater than or equal to the input argument *!
!* *!
!****************************************************************************!
function minpower2( n, log2n )
!
! Arguments:
! n: integer*4, (in), input number
! log2n: integer*4, (out), log base 2 of the function result
! Function return:
! minpower2: integer*4 (out), smallest number, which is a power of 2
! and greater than or equal to n.
!
integer n, minpower2, log2n
!
! Local variables.
integer m, i
m=n
if( n < 0 ) write(*,*) 'n cannot be negative'
powerloop: do i= 1, bit_size(n)
m = m / 2
if( m .eq. 0 ) exit powerloop
enddo powerloop
if ( 2**(i-1) .ne. n ) then
if( 2**i < 0) write(*,*) 'n too large'
log2n = i
minpower2 = 2**i
else
log2n = i-1
minpower2 = n
endif
return
end function minpower2
end module fourier
&input ly_ratio = 1.0, delta_t = .1, nx =15, ny=15, numx = 5, numy =5, numt=20, init_f=1, diff_f =3 /
0: point # X Y 0: 1 0.5236 0.5236 0: 2 1.0472 0.5236 0: 3 1.5708 0.5236 0: 4 2.0944 0.5236 0: 5 2.6180 0.5236 0: 6 0.5236 1.0472 0: 7 1.0472 1.0472 0: 8 1.5708 1.0472 0: 9 2.0944 1.0472 0: 10 2.6180 1.0472 0: 11 0.5236 1.5708 0: 12 1.0472 1.5708 0: 13 1.5708 1.5708 0: 14 2.0944 1.5708 0: 15 2.6180 1.5708 0: 16 0.5236 2.0944 0: 17 1.0472 2.0944 0: 18 1.5708 2.0944 0: 19 2.0944 2.0944 0: 20 2.6180 2.0944 0: 21 0.5236 2.6180 0: 22 1.0472 2.6180 0: 23 1.5708 2.6180 0: 24 2.0944 2.6180 0: 25 2.6180 2.6180 0: 0: 0: Points 0: TIME # 1 # 2 # 3 # 4 # 5 # 6 0: 0.10000 1.62046 2.69937 3.06225 2.69937 1.62046 2.58264 0: 0.20000 1.41067 2.41366 2.76175 2.41366 1.41067 2.24055 0: 0.30000 1.23798 2.15271 2.48036 2.15271 1.23798 1.95718 0: 0.40000 1.09075 1.91572 2.21798 1.91572 1.09075 1.71506 0: 0.50000 0.96250 1.70103 1.97560 1.70103 0.96250 1.50484 0: 0.60000 0.84945 1.50710 1.75384 1.50710 0.84945 1.32086 0: 0.70000 0.74925 1.33257 1.55266 1.33257 0.74925 1.15925 0: 0.80000 0.66027 1.17611 1.37141 1.17611 0.66027 1.01707 0: 0.90000 0.58127 1.03638 1.20907 1.03638 0.58127 0.89197 0: 1.00000 0.51121 0.91203 1.06432 0.91203 0.51121 0.78192 0: 1.10000 0.44919 0.80169 0.93574 0.80169 0.44919 0.68518 0: 1.20000 0.39438 0.70404 0.82187 0.70404 0.39438 0.60020 0: 1.30000 0.34601 0.61781 0.72126 0.61781 0.34601 0.52560 0: 1.40000 0.30340 0.54179 0.63255 0.54179 0.30340 0.46016 0: 1.50000 0.26591 0.47487 0.55444 0.47487 0.26591 0.40277 0: 1.60000 0.23295 0.41604 0.48576 0.41604 0.23295 0.35247 0: 1.70000 0.20401 0.36436 0.42543 0.36436 0.20401 0.30841 0: 1.80000 0.17861 0.31901 0.37249 0.31901 0.17861 0.26982 0: 1.90000 0.15634 0.27924 0.32605 0.27924 0.15634 0.23604 0: 2.00000 0.13682 0.24438 0.28535 0.24438 0.13682 0.20647 0: 0: Points 0: TIME # 7 # 8 # 9 # 10 # 11 # 12 0: 0.10000 4.31793 4.90301 4.31793 2.58264 2.85249 4.78806 0: 0.20000 3.84769 4.40918 3.84769 2.24055 2.43863 4.20461 0: 0.30000 3.41303 3.93800 3.41303 1.95718 2.10266 3.67816 0: 0.40000 3.01815 3.49799 3.01815 1.71506 1.82146 3.21228 0: 0.50000 2.66276 3.09466 2.66276 1.50484 1.58234 2.80362 0: 0.60000 2.34497 2.72994 2.34497 1.32086 1.37711 2.44657 0: 0.70000 2.06219 2.40319 2.06219 1.15925 1.19994 2.13515 0: 0.80000 1.81149 2.11234 1.81149 1.01707 1.04644 1.86371 0: 0.90000 1.58985 1.85460 1.58985 0.89197 0.91312 1.62712 0: 1.00000 1.39435 1.62693 1.39435 0.78192 0.79712 1.42087 0: 1.10000 1.22220 1.42626 1.22220 0.68518 0.69609 1.24100 0: 1.20000 1.07081 1.24971 1.07081 0.60020 0.60802 1.08410 0: 1.30000 0.93783 1.09457 0.93783 0.52560 0.53119 0.94718 0: 1.40000 0.82111 0.95838 0.82111 0.46016 0.46415 0.82766 0: 1.50000 0.71874 0.83892 0.71874 0.40277 0.40561 0.72330 0: 1.60000 0.62901 0.73420 0.62901 0.35247 0.35450 0.63215 0: 1.70000 0.55039 0.64244 0.55039 0.30841 0.30985 0.55254 0: 1.80000 0.48154 0.56208 0.48154 0.26982 0.27084 0.48298 0: 1.90000 0.42125 0.49171 0.42125 0.23604 0.23676 0.42220 0: 2.00000 0.36848 0.43011 0.36848 0.20647 0.20697 0.36908 0: 0: Points 0: TIME # 13 # 14 # 15 # 16 # 17 # 18 0: 0.10000 5.44297 4.78806 2.85249 2.45333 4.13480 4.70628 0: 0.20000 4.82635 4.20461 2.43863 2.04155 3.53366 4.06306 0: 0.30000 4.25037 3.67816 2.10266 1.72459 3.02543 3.50098 0: 0.40000 3.72711 3.21228 1.82146 1.47101 2.59910 3.01855 0: 0.50000 3.26069 2.80362 1.58234 1.26277 2.23988 2.60657 0: 0.60000 2.84936 2.44657 1.37711 1.08877 1.93538 2.25472 0: 0.70000 2.48867 2.13515 1.19994 0.94166 1.67587 1.95359 0: 0.80000 2.17330 1.86371 1.04644 0.81630 1.45370 1.69519 0: 0.90000 1.89793 1.62712 0.91312 0.70885 1.26279 1.47284 0: 1.00000 1.65761 1.42087 0.79712 0.61636 1.09824 1.28104 0: 1.10000 1.44792 1.24100 0.69609 0.53650 0.95604 1.11524 0: 1.20000 1.26492 1.08410 0.60802 0.46739 0.83291 0.97163 0: 1.30000 1.10520 0.94718 0.53119 0.40745 0.72611 0.84705 0: 1.40000 0.96575 0.82766 0.46415 0.35539 0.63334 0.73883 0: 1.50000 0.84399 0.72330 0.40561 0.31012 0.55266 0.64471 0: 1.60000 0.73764 0.63215 0.35450 0.27071 0.48243 0.56279 0: 1.70000 0.64474 0.55254 0.30985 0.23638 0.42125 0.49142 0: 1.80000 0.56358 0.48298 0.27084 0.20646 0.36792 0.42920 0: 1.90000 0.49265 0.42220 0.23676 0.18036 0.32140 0.37493 0: 2.00000 0.43067 0.36908 0.20697 0.15758 0.28081 0.32758 0: 0: Points 0: TIME # 19 # 20 # 21 # 22 # 23 # 24 0: 0.10000 4.13480 2.45333 1.42982 2.41948 2.75758 2.41948 0: 0.20000 3.53366 2.04155 1.14813 1.99356 2.29549 1.99356 0: 0.30000 3.02543 1.72459 0.95015 1.67033 1.93488 1.67033 0: 0.40000 2.59910 1.47101 0.79960 1.41458 1.64393 1.41458 0: 0.50000 2.23988 1.26277 0.67989 1.20679 1.40486 1.20679 0: 0.60000 1.93538 1.08877 0.58206 1.03495 1.20593 1.03495 0: 0.70000 1.67587 0.94166 0.50068 0.89108 1.03879 0.89108 0: 0.80000 1.45370 0.81630 0.43217 0.76952 0.89732 0.76952 0: 0.90000 1.26279 0.70885 0.37401 0.66612 0.77685 0.66612 0: 1.00000 1.09824 0.61636 0.32432 0.57769 0.67376 0.57769 0: 1.10000 0.95604 0.53650 0.28168 0.50176 0.58522 0.50176 0: 1.20000 0.83291 0.46739 0.24495 0.43633 0.50892 0.43633 0: 1.30000 0.72611 0.40745 0.21322 0.37981 0.44300 0.37981 0: 1.40000 0.63334 0.35539 0.18576 0.33088 0.38592 0.33088 0: 1.50000 0.55266 0.31012 0.16193 0.28844 0.33642 0.28844 0: 1.60000 0.48243 0.27071 0.14124 0.25158 0.29343 0.25158 0: 1.70000 0.42125 0.23638 0.12325 0.21953 0.25604 0.21953 0: 1.80000 0.36792 0.20646 0.10759 0.19163 0.22350 0.19163 0: 1.90000 0.32140 0.18036 0.09395 0.16733 0.19516 0.16733 0: 2.00000 0.28081 0.15758 0.08205 0.14614 0.17045 0.14614 0: 0: Points 0: TIME # 25 # 26 # 27 # 28 # 29 # 30 0: 0.10000 1.42982 0: 0.20000 1.14813 0: 0.30000 0.95015 0: 0.40000 0.79960 0: 0.50000 0.67989 0: 0.60000 0.58206 0: 0.70000 0.50068 0: 0.80000 0.43217 0: 0.90000 0.37401 0: 1.00000 0.32432 0: 1.10000 0.28168 0: 1.20000 0.24495 0: 1.30000 0.21322 0: 1.40000 0.18576 0: 1.50000 0.16193 0: 1.60000 0.14124 0: 1.70000 0.12325 0: 1.80000 0.10759 0: 1.90000 0.09395 0: 2.00000 0.08205