Guide and Reference

Fourier Transforms (HPF)

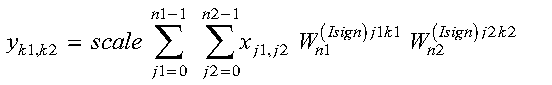
This chapter describes the Fourier Transforms subroutines that can be called from an HPF program.

Overview of the Fourier Transforms Subroutines

The Fourier transform subroutines perform mixed-radix transforms of in two and three dimensions. These subroutines are available in short- and long-precision versions. See references [1] and [3].

Table 139. List of Fourier Transform Subroutines (HPF)

Descriptive Name Short- and Long-Precision Subroutine Page
Fourier Transforms in Two Dimensions FFT FFT--Fourier Transforms in Two Dimensions
Fourier Transforms in Three Dimensions FFT FFT--Fourier Transforms in Three Dimensions

Descriptive Name	Short- and Long-Precision Subroutine	Page
Fourier Transforms in Two Dimensions	FFT	FFT--Fourier Transforms in Two Dimensions
Fourier Transforms in Three Dimensions	FFT	FFT--Fourier Transforms in Three Dimensions

Acceptable Lengths for the Transforms

Use the following formula to determine acceptable transform lengths:

n = (2^h) (3ⁱ) (5^j) (7^k) (11^m) for n <= 37748736

where:

h = 1, 2, ..., 25

i = 0, 1, 2

j, k, m = 0, 1

Figure 13 lists all the acceptable values for transform lengths in the Fourier transform subroutines.

Figure 13. Table of Acceptable Lengths for the Transforms

2 4 6 8 10 12 14 16 18 20 22 24 28 30 32 36 40 42 44 48 56 60 64 66 70 72 80 84 88 90 96 110 112 120 126 128 132 140 144 154 160 168 176 180 192 198 210 220 224 240 252 256 264 280 288 308 320 330 336 352 360 384 396 420 440 448 462 480 504 512 528 560 576 616 630 640 660 672 704 720 768 770 792 840 880 896 924 960 990 1008 1024 1056 1120 1152 1232 1260 1280 1320 1344 1386 1408 1440 1536 1540 1584 1680 1760 1792 1848 1920 1980 2016 2048 2112 2240 2304 2310 2464 2520 2560 2640 2688 2772 2816 2880 3072 3080 3168 3360 3520 3584 3696 3840 3960 4032 4096 4224 4480 4608 4620 4928 5040 5120 5280 5376 5544 5632 5760 6144 6160 6336 6720 6930 7040 7168 7392 7680 7920 8064 8192 8448 8960 9216 9240 9856 10080 10240 10560 10752 11088 11264 11520 12288 12320 12672 13440 13860 14080 14336 14784 15360 15840 16128 16384 16896 17920 18432 18480 19712 20160 20480 21120 21504 22176 22528 23040 24576 24640 25344 26880 27720 28160 28672 29568 30720 31680 32256 32768 33792 35840 36864 36960 39424 40320 40960 42240 43008 44352 45056 46080 49152 49280 50688 53760 55440 56320 57344 59136 61440 63360 64512 65536 67584 71680 73728 73920 78848 80640 81920 84480 86016 88704 90112 92160 98304 98560 101376 107520 110880 112640 114688 118272 122880 126720 129024 131072 135168 143360 147456 147840 157696 161280 163840 168960 172032 177408 180224 184320 196608 197120 202752 215040 221760 225280 229376 236544 245760 253440 258048 262144 270336 286720 294912 295680 315392 322560 327680 337920 344064 354816 360448 368640 393216 394240 405504 430080 443520 450560 458752 473088 491520 506880 516096 524288 540672 573440 589824 591360 630784 645120 655360 675840 688128 709632 720896 737280 786432 788480 811008 860160 887040 901120 917504 946176 983040 1013760 1032192 1048576 1081344 1146880 1179648 1182720 1261568 1290240 1310720 1351680 1376256 1419264 1441792 1474560 1572864 1576960 1622016 1720320 1774080 1802240 1835008 1892352 1966080 2027520 2064384 2097152 2162688 2293760 2359296 2365440 2523136 2580480 2621440 2703360 2752512 2838528 2883584 2949120 3145728 3153920 3244032 3440640 3548160 3604480 3670016 3784704 3932160 4055040 4128768 4194304 4325376 4587520 4718592 4730880 5046272 5160960 5242880 5406720 5505024 5677056 5767168 5898240 6291456 6307840 6488064 6881280 7096320 7208960 7340032 7569408 7864320 8110080 8257536 8388608 8650752 9175040 9437184 9461760 10092544 10321920 10485760 10813440 11010048 11354112 11534336 11796480 12582912 12615680 12976128 13762560 14192640 14417920 14680064 15138816 15728640 16220160 16515072 16777216 17301504 18350080 18874368 18923520 20185088 20643840 20971520 21626880 22020096 22708224 23068672 23592960 25165824 25231360 25952256 27525120 28385280 28835840 29360128 30277632 31457280 32440320 33030144 33554432 34603008 36700160 37748736

Fourier Transforms Subroutines

This section contains the Fourier transform subroutine descriptions.

FFT--Fourier Transforms in Two Dimensions

These subroutines compute the mixed-radix two-dimensional discrete Fourier transform of short- or long-precision data:

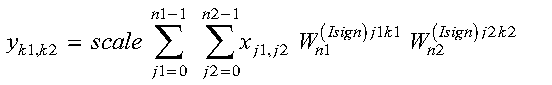
for:

k1 = 0, 1, ..., n1-1

k2 = 0, 1, ..., n2-1

where:

and where:

x_j1,j2 are elements of array X.

y_k1,k2 are elements of array Y.

Isign is + or - (determined by argument isign).

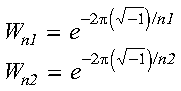
scale is a scalar value.

For scale = 1 and isign being positive, you obtain the discrete Fourier transform. For scale = 1/((n1)(n2)) and isign being negative, you obtain the inverse Fourier transform.

See references [1] and [3].

Table 140. Data Types and Sizes for X and Y

Short- and Long-Precision Data Types Size of Assumed-Shaped Array X Size of Assumed-Shaped Array Y
Case 1:
Complex-to-Complex
n1 × n2 n2 × n1 (output is stored in transposed format)
n1 × n2 (output is stored in normal format)
If transpose is not specified, see the transpose argument and its default description to find out how the output is stored.
Case 2:
Real-to-Complex
n1 × n2 n2 × n1/2^&
Case 3:
Complex-to-Real
n2 × n1/2^& n1 × n2

^& This array is stored in FFT-packed storage mode.
Notes for All Cases:

n1 and n2 must be fullword integers that are less than or equal to 37748736, and must be one of the values listed in Figure 13.
For Cases 1 and 2:

n1 = size(x,1)
n2 = size(x,2)

For Case 3:

n1 = 2(size(x,2))
n2 = size(x,1)

scale is a short- or long-precision real number that must be of the same precision as both x and y.

Syntax

HPF	Case 1	CALL FFT (`x`) CALL FFT (`x`, `y`, `transpose`, `isign`, `scale`)
HPF	Cases 2 and 3	CALL FFT (`x,` `y`) CALL FFT (`x`, `y`, `isign`, `scale`)

On Entry

x

is the array X containing the two-dimensional data to be transformed.

Type: required

Specified as: an assumed-shape array with shape (:,:), containing numbers of the data type indicated in Table 140. This array must be aligned on a doubleword boundary.

y

See 'On Return'.

transpose

has the following meaning:

If y is specified, array Y contains the results of the computation, where:
If transpose = 'T', y is returned in transposed form; that is, y has dimensions n2 × n1.
If transpose = 'N', y is returned in normal form; that is, y has dimensions n1 × n2.
For case 1, if y is not specified, array X contains the result of the computation, where:
If transpose = 'T', x is returned in transposed form; that is, x has dimensions n2 × n1.
If transpose = 'N', x is returned in normal form; that is, x has dimensions n1 × n2.

Type: optional (case 1); not present (cases 2 and 3)

Default:

For case 1, if transpose is not present, the subroutine returns the output in transposed form if the output array has a shape which is the transpose of the shape of the input array X. Otherwise, the output is returned in normal form, as follows:

n1 = n2, the output array is stored in transposed form and has dimensions n2 × n1
n1 <> n2 and the output array has dimensions n2 × n1, the output array is stored in transposed form.
n1 <> n2 and the output array has dimensions n1 × n2, the output array is stored in normal form.

Specified as: a single character; transpose = 'T' or 'N'.

isign

controls the direction of the transform, determining the sign, isign, of the exponent of W_n, where:

If isign = positive value, Isign = + (transforming time to frequency).

If isign = negative value, Isign = - (transforming frequency to time).

Type: optional

Default: isign is a positive value.

Specified as: a fullword integer; where isign > 0 or isign < 0.

scale

is the scaling constant scale.

Type: optional

Default: scale has the following value, where:

If isign is a positive value or is not specified, scale = 1.
If isign is negative, scale = 1/((n1)(n2)).

Specified as: a number of the data type indicated in Table 140, where scale > 0.0 or scale < 0.0.

On Return

x

can only be returned in the complex-to-complex subroutines (case 1) and has the following meaning:

If y is specified, array Y contains the results of the computation and x is not returned.
If y is not specified, array X contains the result of the computation, where:
If transpose = 'T', x is returned in transposed form; that is, x has dimensions n2 × n1. In this case, n1 must equal n2.
If transpose = 'N', x is returned in normal form; that is x has dimensions n1 × n2.
In this case, output overwrites input.

Returned as: an assumed-shape array with shape (:,:), containing the numbers of the data type indicated in Table 140. This array must be aligned on a doubleword boundary.

y

has the following meaning:

If y is specified, array Y contains the results of the computation, where:
If transpose = 'T', y is returned in transposed form; that is, y has dimensions n2 × n1.
If transpose = 'N', y is returned in normal form; that is y has dimensions n1 × n2
In this case, X and Y must have no common elements; otherwise, results are unpredictable.
For case 1, if y is not specified, array X contains the result of the computation.

Type: optional (case 1); required (cases 2 and 3)

Default: Array X contains the result of the computation.

Returned as: an assumed-shape array with shape (:,:), containing the numbers of the data type indicated in Table 140. This array must be aligned on a doubleword boundary.

Notes and Coding Rules

All subroutines accept lowercase letters for the transpose argument.
The x, y, and scale arguments must be of the same precision.
The assumed shape arrays must have no common elements; otherwise, results are unpredictable.
If the output array does not have the correct shape for storing the transformed data, an error message is issued and the application program is terminated. However, this error check occurs before the problem size is verified to consist of only valid transform lengths. This means that if you correct the shape and rerun the program, you may still receive an additional error message if the values for the problem size are not valid transform lengths.
An example of the use of this subroutine in a thermal diffusion application program is shown in Appendix B. "Sample Programs". See subroutine fourier in "Module Fourier (HPF)".
For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"
Block-column data distribution is required for your array data. In general, distributing your data evenly provides the best work load balance among the processes and allows the use of the most efficient collective communication. However, for your specific problem size and number of processes available, experimentation is necessary to achieve optimal performance.
Because data directives are included in the interface module PESSL_HPF, you can specify any data distribution for your sequences, and the XL HPF compiler will, if necessary, redistribute the data prior to calling this subroutine. For how to code your HPF directives, see "Sequences (Fourier Transform)". For a sample program including directives, see Figure 10.
The restrictions given in "Notes and Coding Rules", "Notes and Coding Rules", and "Notes and Coding Rules" also apply to this subroutine.

Error Conditions

HPF-specific errors are listed below. Resource and input-argument errors listed in "Error Conditions", "Error Conditions", and "Error Conditions" also apply to these subroutines.

Input-Argument Errors for Case 1

Stage 1

The rank of the ultimate align target is greater than 1 for x or y.
The process rank is not the same for x and y.
The process rank is not 1 for x or y.

Stage 2

The process grid is not the same for x and y.
The data distribution is unsupported for x or y.

Stage 3

transpose is present and transpose <> 'N' or 'T'

Stage 4

If transpose = 'T' and y is present and the shape of y is not n2 × n1.
If transpose = 'N' and y is present and the shape of y is not n1 × n2.
If y is not present (which means x contains the result of the computation) and transpose = 'T' and n1 <> n2.

Input-Argument Errors for Cases 2 and 3

Stage 1

The rank of the ultimate align target is greater than 1 for x or y.
The process rank is not the same for x and y.
The process rank is not 1 for x or y.

Stage 2

The process grid is not the same for x and y.
The data distribution is unsupported for x or y.

Stage 3

The shape of the assumed-shape arrays x and y are incompatible, as follows:
For case 2:

2(size(y,2)) <> n1 or
size(y,1) <> n2

For case 3:

size(y,2) <> n2 or
size(y,1) <> n1

Example 1

This example shows how to compute a complex-to-complex, two-dimensional transform. As in "Example 1", the array data is block-column distributed using a one-dimensional process grid with two processes. Array Y is returned in transposed form. The arrays are declared as follows:

COMPLEX*16 X(0:7,0:5), Y(0:5,0:7)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X , Y , ISIGN=-1 )
-or-
CALL FFT( X , Y , TRANSPOSE='T' , ISIGN=-1 , SCALE=1.0D0/48.0D0 )

Matrix X of order 8 × 6:

 *                                                                        *
 | (48.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 |  (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0)   (0.0,0.0) |
 *                                                                        *

Output

Matrix for Y:

 *                                                                                        *
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 *                                                                                        *

Example 2

This example shows how to compute a real-to-complex, two-dimensional transform. As in "Example", the array data is block-column distributed using a one-dimensional process grid with two processes. The arrays are declared as follows:

REAL*8 X(0:11,0:3)
COMPLEX*16 Y(0:6,0:3)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X(0:7,0:3) , Y(0:3,0:3))
-or-
CALL FFT( X(0:7,0:3) , Y(0:3,0:3) , ISIGN=1 , SCALE=1.0D0 )

Matrix X of order 8 × 4:

 *                    *
 | 1.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Output

The following matrix Y is returned in transposed form and stored in FFT-packed storage mode:

 *                                            *
 | (1.0,1.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,1.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 |     .          .          .          .     |
 |     .          .          .          .     |
 *                                            *

Example 3

This example shows how to compute a complex-to-real, two-dimensional transform. As in "Example", the array data is block-column distributed using a one-dimensional process grid with two processes. The arrays are declared as follows:

COMPLEX*16 X(0:6,0:3)
REAL*8 Y(0:11,0:3)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X(0:3,0:3) , Y(0:7,0:3) ISIGN=-1 )
-or-
CALL FFT( X(0:3,0:3) , Y(0:7,0:3) , ISIGN=-1 , SCALE=1.0D0/32.0D0 )

The following matrix X is stored in FFT-packed storage mode:

 *                                            *
 | (1.0,1.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,1.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 |     .          .          .          .     |
 |     .          .          .          .     |
 *                                            *

Output

Matrix Y:

 *                    *
 | 1.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

FFT--Fourier Transforms in Three Dimensions

These subroutines compute the mixed-radix three-dimensional discrete Fourier transform of short- or long-precision data:

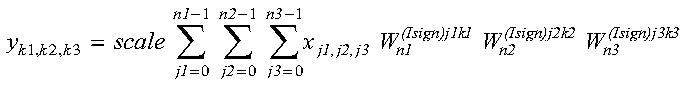
for:

k1 = 0, 1, ..., n1-1

k2 = 0, 1, ..., n2-1

k3 = 0, 1, ..., n3-1

where:

and where:

x_j1,j2,j3 are elements of array X.

y_k1,k2,k3 are elements of array Y.

Isign is + or - (determined by argument isign).

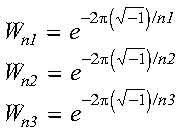
scale is a scalar value.

For scale = 1 and isign being positive, you obtain the discrete Fourier transform. For scale = 1/((n1)(n2)(n3)) and isign being negative, you obtain the inverse Fourier transform.

See references [1] and [3].

Table 141. Data Types and Sizes for X and Y

Short- and Long-Precision Data Types Size of Assumed-Shaped Array X Size of Assumed-Shaped Array Y
Case 1:
Complex-to-Complex
n1 × n2 × n3 n3 × n2 × n1 (output is stored in transposed format)
n1 × n2 × n3 (output is stored in normal format)
If transpose is not specified, see the transpose argument and its default description to find out how the output is stored.
Case 2:
Real-to-Complex
n1 × n2 × n3 n3 × n2 × n1/2^&
Case 3:
Complex-to-Real
n3 × n2 × n1/2^& n1 × n2 × n3

^& This array is stored in FFT-packed storage mode.
Notes for All Cases:

n1, n2, n3 must be fullword integers that are less than or equal to 37748736, and must be one of the values listed in Figure 13.
For cases 1 and 2:

n1 = size(x,1)
n2 = size(x,2)
n3 = size(x,3)

For case 3:

n1 = 2(size(x,3))
n2 = size(x,2)
n3 = size(x,1)

scale is a short- or long-precision real number that must be of the same precision as both x and y.

Syntax

HPF	Case 1	CALL FFT (`x`) CALL FFT (`x`, `y`, `transpose`, `isign`, `scale`,)
HPF	Cases 2 and 3	CALL FFT (`x,` `y`) CALL FFT (`x`, `y`, `isign`, `scale`)

On Entry

x

is the array X containing the three-dimensional data to be transformed.

Type: required

Specified as: an assumed-shape array with shape (:,:,:), containing numbers of the data type indicated in Table 141. This array must be aligned on a doubleword boundary.

y

See 'On Return'.

transpose

has the following meaning:

If y is specified, array Y contains the result of the computation, where:
If transpose = 'T', y is returned in transposed form; that is, y has dimensions n3 × n2 × n1
If transpose = 'N', y is returned in normal form; that is, y has dimensions n1 × n2 × n3.
For case 1, if y is not specified, array X contains the result of the computation, where:
If transpose = 'T', x is returned in transposed form; that is, x has dimensions n3 × n2 × n1.
If transpose = 'N', x is returned in normal form; that is, x has dimensions n1 × n2 × n3.

Type: optional (case 1); not present (cases 2 and 3)

Default:

n1 = n3, the output array is stored in transposed form and has dimensions n3 × n2 × n1
n1 <> n3 and the output array has dimensions n3 × n2 × n1, the output array is stored in transposed form.
n1 <> n3 and the output array has dimensions n1 × n2 × n3, the output array is stored in normal form.

Specified as: a single character; transpose = 'T' or 'N'.

isign

controls the direction of the transform, determining the sign, isign, of the exponent of W_n, where:

If isign = positive value, Isign = + (transforming time to frequency).

If isign = negative value, Isign = - (transforming frequency to time).

Type: optional

Default: isign is a positive value.

Specified as: a fullword integer; where isign > 0 or isign < 0.

scale

is the scaling constant scale.

Type: optional

Default: scale has the following value, where:

If isign is a positive value or is not specified, scale = 1.
If isign is negative, scale = 1/((n1)(n2)(n3)).

Specified as: a number of the data type indicated in Table 141, where scale > 0.0 or scale < 0.0.

On Return

x

can only be returned in the complex-to-complex subroutines (case 1) and has the following meaning:

If y is specified, array Y contains the result of the computation and x is not returned.
If y is not specified, array X contains the result of the computation, where:
If transpose = 'T', x is returned in transposed form; that is, x has dimensions n3 × n2 × n1. In this case, n1 must equal n3.
If transpose = 'N', x is returned in normal form; that is, x has dimensions n1 × n2 × n3.
In this case, output overwrites input.

Returned as: an assumed-shape array with shape (:,:,:), containing numbers of the data type indicated in Table 141. This array must be aligned on a doubleword boundary.

y

has the following meaning:

If y is specified, array Y contains the results of the computation, where:
If transpose = 'T', y is returned in transposed form; that is, y has dimensions n3 × n2 × n1
If transpose = 'N', y is returned in normal form; that is, y has dimensions n1 × n2 × n3
In this case, X and Y must have no common elements; otherwise, results are unpredictable.
For case 1, if y is not specified, array X contains the result of the computation.

Type: optional (case 1); required (cases 2 and 3)

Default: Array X contains the result of the computation. This array must be aligned on a doubleword boundary.

Returned as: an assumed-shape array with shape (:,:,:), containing the numbers of the data type indicated in Table 141. This array must be aligned on a doubleword boundary.

Notes and Coding Rules

All subroutines accept lowercase letters for the transpose argument.
The x, y, and scale arguments must be of the same precision.
The assumed shape arrays must have no common elements; otherwise, results are unpredictable.
If the output array does not have the correct shape for storing the transformed data, an error message is issued and the application program is terminated. However, this error check occurs before the problem size is verified to consist of only valid transform lengths. This means that if you correct the shape and rerun the program, you may still receive an additional error message if the values for the problem size are not valid transform lengths.
An example of the use of this subroutine in a thermal diffusion application program is shown in Appendix B. "Sample Programs". See subroutine fourier in "Module Fourier (HPF)".
For details on how to set up and code your HPF program using Parallel ESSL, see "Coding Your HPF Program"
Block-column data distribution is required for your array data. In general, distributing your data evenly provides the best work load balance among the processes and allows the use of the most efficient collective communication. However, for your specific problem size and number of processes available, experimentation is necessary to achieve optimal performance.
Because data directives are included in the interface module PESSL_HPF, you can specify any data distribution for your sequences, and the XL HPF compiler will, if necessary, redistribute the data prior to calling this subroutine. For how to code your HPF directives, see "Sequences (Fourier Transform)". For a sample program including directives, see Figure 10.
The restrictions given in "Notes and Coding Rules", "Notes and Coding Rules", and "Notes and Coding Rules" also apply to this subroutine.

Error Conditions

HPF-specific errors are listed below. Resource and input-argument errors listed in "Error Conditions", "Error Conditions", and "Error Conditions" also apply to these subroutines.

Input-Argument Errors for Case 1

Stage 1

The rank of the ultimate align target is greater than 1 for x or y.
The process rank is not the same for x and y.
The process rank is not 1 for x or y.

Stage 2

The process grid is not the same for x and y.
The data distribution is unsupported for x or y.

Stage 3

transpose is present and transpose <> 'N' or 'T'

Stage 4

If transpose = 'T' and y is present and the shape of y is not n3 × n2 × n1.
If transpose = 'N' and y is present and the shape of y is not n1 × n2 × n3.
If y is not present (which means x contains the result of the computation) and transpose = 'T' and n1 <> n3.

Input-Argument Errors for Cases 2 and 3

Stage 1

The rank of the ultimate align target is greater than 1 for x or y.
The process rank is not the same for x and y.
The process rank is not 1 for x or y.

Stage 2

The process grid is not the same for x and y.
The data distribution is unsupported for x or y.

Stage 3

The shape of the assumed-shape arrays x and y are incompatible, as follows:
For case 2:

2(size(y,3)) <> n1 or
size(y,2) <> n2 or
size(y,1) <> n3

For case 3:

size(y,3) <> n3 or
size(y,2) <> n2 or
size(y,1)) <> n1

Example 1

This example shows how to compute a complex-to-complex, three-dimensional transform. As in "Example", the array data is block-plane distributed using a one-dimensional process grid with two processes. The arrays are declared as follows:

COMPLEX*16 X(0:3,0:3,0:1)
COMPLEX*16 Y(0:3,0:3,0:1)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, *, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X , Y )
-or-
CALL FFT( X , Y , TRANSPOSE='N', ISIGN=1 , SCALE=1.0D0 )

Following is matrix X in two planes:

Plane 0:

 *                                            *
 | (1.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 *                                            *

Plane 1:

 *                                            *
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 | (0.0,0.0)  (0.0,0.0)  (0.0,0.0)  (0.0,0.0) |
 *                                            *

Output

Following is matrix Y:

Plane 0:

 *                                            *
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 *                                            *

Plane 1:

 *                                            *
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 *                                            *

Example 2

This example shows how to compute a real-to-complex, three-dimensional transform. As in "Example", the array data is block-plane distributed using a one-dimensional process grid with two processes. The arrays are declared as follows:

REAL*8 X(0:8,0:3,0:3)
COMPLEX*16 Y(0:4,0:3,0:1)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, *, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X(0:3,0:3,0:3) , Y(0:3,0:3,0:1) )
-or-
CALL FFT( X(0:3,0:3,0:3) , Y(0:3,0:3,0:1) , ISIGN=1 , SCALE=1.0D0 )

Following is matrix X in four planes:

Plane 0:

 *                    *
 | 1.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 1:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 2:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 3:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Output

The following matrix Y is returned in transposed form and stored in FFT-packed storage mode:

Plane 0:

 *                                            *
 | (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 *                                            *

Plane 1:

 *                                            *
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 *                                            *

Example 3

This example shows how to compute a complex-to-real, three-dimensional transform. As in "Example", the array data is block-plane distributed using a one-dimensional process grid with two processes. Array Y is returned in transposed form. The arrays are declared as follows:

COMPLEX*16 X(0:4,0:3,0:1)
REAL*8 Y(0:8,0:3,0:3)
REAL*8 SCALE

Input

!HPF$ PROCESSORS PROC(2)
!HPF$ DISTRIBUTE (*, *, BLOCK) ONTO PROC :: X, Y
 
CALL FFT( X(0:3,0:3,0:1) , Y(0:3,0:3,0:3) , ISIGN=-1 )
-or-
CALL FFT( X(0:3,0:3:0:1) , Y(0:3,0:3,0:3) , ISIGN=-1 , SCALE=1.0D0/64.0D0 )

The following matrix X is stored in FFT-packed storage mode:

Plane 0:

 *                                            *
 | (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 *                                            *

Plane 1:

 *                                            *
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 | (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 |     .          .          .          .     |
 *                                            *

Output

The following matrix Y is returned:

Plane 0:

 *                    *
 | 1.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 1:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 2:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

Plane 3:

 *                    *
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 | 0.0  0.0  0.0  0.0 |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 |  .    .    .    .  |
 *                    *

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]