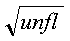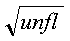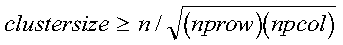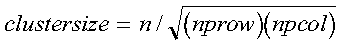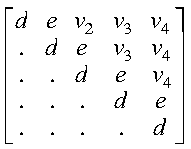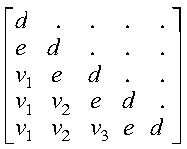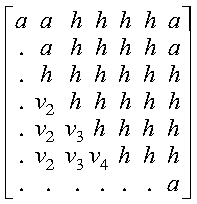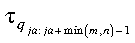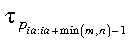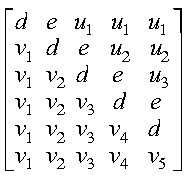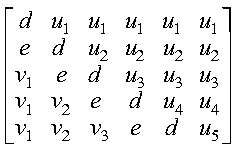Guide and Reference

Eigensystem Analysis and Singular Value Analysis (Message Passing)

This chapter describes the eigensystem analysis and singular value analysis subroutines.

Overview of the Eigensystem Analysis and Singular Value Analysis Subroutines

The eigensystem analysis and singular value analysis subroutines include a subset of the ScaLAPACK subroutines. See references [19] and [20].
Note: These subroutines are designed in accordance with the proposed ScaLAPACK standard. If these subroutines do no comply with the standard as approved, IBM will consider updating them to do so. If IBM updates these subroutines, the update could require modifications of the calling application program.

Table 95. List of Eigensystem Analysis and Singular Value Analysis Subroutines (Message Passing)

Descriptive Name Long-Precision Subroutine Page
Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix PDSYEVX PDSYEVX--Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix
Reduce a Real Symmetric Matrix to Tridiagonal Form PDSYTRD PDSYTRD--Reduce a Real Symmetric Matrix to Tridiagonal Form
Reduce a General Matrix to Upper Hessenberg Form PDGEHRD PDGEHRD--Reduce a General Matrix to Upper Hessenberg Form
Reduce a General Matrix to Bidiagonal Form PDGEBRD PDGEBRD--Reduce a General Matrix to Bidiagonal Form

Descriptive Name	Long-Precision Subroutine	Page
Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix	PDSYEVX	PDSYEVX--Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix
Reduce a Real Symmetric Matrix to Tridiagonal Form	PDSYTRD	PDSYTRD--Reduce a Real Symmetric Matrix to Tridiagonal Form
Reduce a General Matrix to Upper Hessenberg Form	PDGEHRD	PDGEHRD--Reduce a General Matrix to Upper Hessenberg Form
Reduce a General Matrix to Bidiagonal Form	PDGEBRD	PDGEBRD--Reduce a General Matrix to Bidiagonal Form

Eigensystem Analysis and Singular Value Analysis Subroutines

This section contains the eigensystem analysis subroutine descriptions.

PDSYEVX--Selected Eigenvalues and, Optionally, the Eigenvectors of a Real Symmetric Matrix

This subroutine computes selected eigenvalues and, optionally, the eigenvectors of a real symmetric matrix A, where A represents the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1}. Eigenvalues and eigenvectors can be selected by specifying a range of values or a range of indices for the eigenvalues.

If n = 0, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13], [24], [25], and [26].

Table 96. Data Types

A, vl, vu, abstol, orfac, Z, w, work, gap iwork, ifail, iclustr Subroutine
Long-precision real Integer PDSYEVX

Syntax

Fortran	CALL PDSYEVX (`jobz`, `range`, `uplo`, `n`, `a`, `ia`, `ja`, `desc_a`, `vl`, `vu`, `il`, `iu`, `abstol`, `m`, `nz`, `w`, `orfac`, `z`, `iz`, `jz`, `desc_z`, `work`, `lwork`, `iwork`, `liwork`, `ifail`, `iclustr`, `gap`, `info`)
C and C++	pdsyevx (`jobz`, `range`, `uplo`, `n`, `a`, `ia`, `ja`, `desc_a`, `vl`, `vu`, `il`, `iu`, `abstol`, `m`, `nz`, `w`, `orfac`, `z`, `iz`, `jz`, `desc_z`, `work`, `lwork`, `iwork`, `liwork`, `ifail`, `iclustr`, `gap`, `info`);

On Entry

jobz

indicates the type of computation to be performed, where:

If jobz = 'N', eigenvalues only are computed.

If jobz = 'V', eigenvalues and eigenvectors are computed.

Scope: global

Specified as: a single character; jobz = 'N' or 'V'.

range

indicates which eigenvalues to compute, where:

If range = 'A', all eigenvalues are to be found.

If range = 'V', all eigenvalues in the interval [vl, vu] are to be found.

If range = 'I', the il-th through iu-th eigenvalues are to be found.

Scope: global

Specified as: a single character; range = 'A', 'V', or 'I'.

uplo

indicates whether the upper or lower triangular part of the global symmetric submatrix A is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Scope: global

Specified as: a single character; uplo = 'U' or 'L'.

n

is the order of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

a

is the local part of the global symmetric matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+n-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+n-1 by ja+n-1 part of the global matrix, and:

If uplo = 'U', the leading n × n upper triangular part of the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1} must contain the upper triangular part of the symmetric matrix, and the strictly lower triangular part is not referenced.
If uplo = 'L', the leading n × n lower triangular part of the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1} must contain the lower triangular part of the symmetric matrix, and the strictly upper triangular part is not referenced.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 96. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+n-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `n` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `n` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

vl

has the following meaning:

If range = 'V', it is the lower bound of the interval to be searched for eigenvalues.

If range <> 'V', this argument is ignored.

Scope: global

Specified as: a number of the data type indicated in Table 96. If range = 'V', vl < vu.

vu

has the following meaning:

If range = 'V', it is the upper bound of the interval to be searched for eigenvalues.

If range <> 'V', this argument is ignored.

Scope: global

Specified as: a number of the data type indicated in Table 96. If range = 'V', vl < vu.

il

has the following meaning:

If range = 'I', it is the index (from smallest to largest) of the smallest eigenvalue to be returned.

If range <> 'I', this argument is ignored.

Scope: global

Specified as: a fullword integer; il >= 1.

iu

has the following meaning:

If range = 'I', it is the index (from smallest to largest) of the largest eigenvalue to be returned.

If range <> 'I', this argument is ignored.

Scope: global

Specified as: a fullword integer; min(il, n) <= iu <= n.

abstol

is the absolute tolerance for the eigenvalues. An approximate eigenvalue is accepted as converged when it is determined to lie in an interval [a, b] of width less than or equal to:

abstol+epsilon(max(|a|, |b|))

where epsilon is the machine precision. If abstol is less than or equal to zero, then epsilon(norm(T)) is used in its place, where norm(T) is the 1-norm of the tridiagonal matrix obtained by reducing A to tridiagonal form. For most problems, this is the appropriate level of accuracy to request.

For certain strongly graded matrices, greater accuracy can be obtained in very small eigenvalues by setting abstol to a very small positive number. However, if abstol is less than:

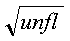
where unfl is the underflow threshold, then:

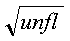
is used in its place.

Eigenvalues are computed most accurately when abstol is set to twice the underflow threshold--that is, (2)(unfl).

If jobz = 'V', then setting abstol to unfl, the underflow threshold, yields the most orthogonal eigenvectors.

Scope: global

Specified as: a number of the data type indicated in Table 96.

m

See 'On Return'.

nz

See 'On Return'.

w

See 'On Return'.

orfac

specifies which eigenvectors should be reorthogonalized. Eigenvectors that correspond to eigenvalues which are within:

ortol = (orfac)(norm(A))

of each other (where norm(A) is the 1-norm of A) are to be reorthogonalized.

However, if the workspace is insufficient (see lwork), ortol may be decreased until all eigenvectors to be reorthogonalized can be stored in one process.

If orfac is zero, no reorthogonalization is done.

If orfac is less than zero, a default value of 10^-3 is used.

Scope: global

Specified as: a number of the data type indicated in Table 96.

z

See 'On Return'.

iz

is the row index of the global matrix Z, identifying the first row of the submatrix Z.

Scope: global

Specified as: a fullword integer; 1 <= iz <= M_Z and iz+n-1 <= M_Z.

jz

is the column index of the global matrix Z, identifying the first column of the submatrix Z.

Scope: global

Specified as: a fullword integer; 1 <= jz <= N_Z and jz+n-1 <= N_Z.

desc_z

is the array descriptor for global matrix Z, described in the following table:

`desc_z`	Name	Description	Limits	Scope
1	DTYPE_Z	Descriptor type	DTYPE_Z=1	Global
2	CTXT_Z	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_Z	Number of rows in the global matrix	If `n` = 0: M_Z >= 0 Otherwise: M_Z >= 1	Global
4	N_Z	Number of columns in the global matrix	If `n` = 0: N_Z >= 0 Otherwise: N_Z >= 1	Global
5	MB_Z	Row block size	MB_Z >= 1	Global
6	NB_Z	Column block size	NB_Z >= 1	Global
7	RSRC_Z	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_Z < `p`	Global
8	CSRC_Z	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_Z < `q`	Global
9	LLD_Z	The leading dimension of the local array	LLD_Z >= max(1,LOCp(M_Z))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is a work area used by this subroutine, where:

If lwork <> -1, then its size is (at least) of length lwork.
If lwork = -1, then its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 96.

lwork

is the number of elements in array WORK.

Scope:

If lwork >= 0, lwork is local.
If lwork = -1, lwork is global.

Specified as: a fullword integer; where:

If lwork = 0, PDSYEVX dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If lwork = -1, PDSYEVX performs a work area query and returns the minimum required size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, use the following rules to determine the value to specify:
- If jobz = 'N', it must have the following value:
  lwork >= 3(n+ja-1)+2n +max(5nn, (nb)(np+1))
- If jobz = 'V', then the amount of workspace required to guarantee that all eigenvectors are computed is:
  lwork >= 3(n+ja-1)+2n +max(5nn, (np0)(mq0)+2(nb)(nb)) + iceil(neig, (nprow)(npcol))(nn)
  where:
  
  nn = max(n, nb, 2)
  neig is the number of eigenvectors requested
  nb = MB_A = NB_A = MB_Z = NB_Z
  np = NUMROC(nn, nb, myrow, iarow, nprow)
  np0 = NUMROC(nn+iroffz, nb, izrow, izrow, nprow)
  mq0 = NUMROC(max(neig, nb, 2)+icoffz, nb, izcol, izcol, npcol)
  iarow = mod(RSRC_A + (ia-1)/nb, nprow)
  izrow = mod(RSRC_Z + (iz-1)/nb, nprow)
  izcol = mod(CSRC_Z + (jz-1)/nb, npcol)
  iroffz = mod(iz-1, MB_Z)
  icoffz = mod(jz-1, NB_Z)
The computed eigenvectors may not be orthogonal if the minimum workspace is supplied and ortol is too small; therefore, if you want to guarantee orthogonality (at the cost of potentially compromising performance), you should add the following to lwork:
(clustersize-1)(n)
where clustersize is the number of eigenvalues in the largest cluster, where a cluster is defined as a set of close eigenvalues:

{w_k, ..., w_{k+iclustrsz-1} | w_j+1 <= w_j+orfac(2)(norm(A))}

Note: This subroutine does not add this amount when dynamically allocating this workspace. You must use static allocation if you want to guarantee orthogonality.

When lwork is too small:
- If lwork is too small to guarantee orthogonality, this subroutine attempts to maintain orthogonality in the clusters with the smallest spacing between the eigenvalues.
- If lwork is too small to compute all the eigenvectors requested, no computation is performed, except that if range = 'V', this subroutine does not know how many eigenvectors are requested until the eigenvalues are computed. Therefore, if range = 'V' and lwork is large enough to allow this subroutine to compute the eigenvalues, this subroutine computes the eigenvalues and as many eigenvectors as it can.
Relationship between workspace, orthogonality, and performance:

If clustersize is:

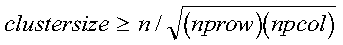
then providing enough space to compute all the eigenvectors orthogonally causes serious degradation in performance. In the limit (clustersize = n-1), performance may be no better than using one process.
If clustersize is:

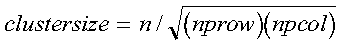
then reorthogonalizing all eigenvectors increases the total execution time by a factor of 2 or more.
If clustersize is:

then execution time grows as the square of the cluster size, assuming all other factors remain equal and there is enough workspace. Less workspace means less reorthogonalization, but faster execution.

iwork

has the following meaning:

If liwork = 0, iwork is ignored.

If liwork <> 0, iwork is a work area used by this subroutine, where:

If liwork <> -1, then its size is (at least) of length liwork.
If liwork = -1, then its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing fullword integers.

liwork

is the number of elements in array IWORK.

Scope:

If liwork >= 0, liwork is local.
If liwork = -1, liwork is global.

Specified as: a fullword integer; where:

If liwork = 0, PDSYEVX dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If liwork = -1, PDSYEVX performs a work area query and returns the minimum required size of iwork in iwork₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, it must have the following value:
liwork >= max(isizestein, isizestebz)+2n
where:
isizestein must have the following value:
- If jobz = 'N', isizestein = 3n+nprocs+1
- If jobz = 'V', isizestein = (n+jz-1) +2n+nprocs+1
isizestebz = max(4n, 14, nprocs)
nprocs = (nprow)(npcol)

ifail

See 'On Return'.

iclustr

See 'On Return'.

gap

See 'On Return'.

info

See 'On Return'.

On Return

a

a is the local part of the global symmetric matrix A, where:

If uplo = 'U', the upper triangle and diagonal of submatrix A_{ia:ia+n-1,
ja:ja+n-1} are overwritten; that is, the original input is not preserved.

If uplo = 'L', the lower triangle and diagonal of submatrix A_{ia:ia+n-1,
ja:ja+n-1} are overwritten; that is, the original input is not preserved.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 96.

m

is the number of eigenvalues found.

Scope: global

Returned as: a fullword integer; 0 <= m <= n.

nz

has the following meaning:

If jobz <> 'V', then nz is ignored.

If jobz = 'V', then nz is the number of eigenvectors computed--that is, the number of columns of Z used in the computation. On output, nz = m unless you provide insufficient space. To get all the eigenvectors requested, you must supply both sufficient space to hold the eigenvectors in Z and sufficient workspace to compute them (see lwork).

If range = 'A' or 'I', PDSYEVX does not perform any computations if the work space supplied is insufficient. In this case, an input-argument error is issued and your job is terminated. For range = 'V', the number of requested eigenvectors is unknown until the eigenvalues are found. In this case, PDSYEVX computes as many eigenvectors as space allows. Then, if nz <> m, a computational error message is issued.

Scope: global

Returned as: a fullword integer; 0 <= nz <= m.

w

On normal exit (see info), it is the vector w, containing the selected eigenvalues in ascending order in the first m elements of w.

Scope: global

Returned as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 96.

z

has the following meaning:

If jobz = 'N', then z is ignored.

If jobz = 'V' and there is a normal exit (see info), then this is the updated local part of the global matrix Z, where columns jz to jz+m-1 of the global matrix Z contain the orthonormal eigenvectors of the global matrix A, corresponding to the selected eigenvalues. If an eigenvector fails to converge, then the corresponding column of the global matrix Z contains the last approximation to the eigenvector, and the index of the eigenvector is returned in ifail.

This identifies the first element of the local array Z. This subroutine computes the location of the first element of the local subarray used, based on iz, jz, desc_z, p, q, myrow, and mycol; therefore, the leading LOCp(iz+n-1) by LOCq(jz+n-1) part of the local array Z must contain the local pieces of the leading iz+n-1 by jz+n-1 part of the global matrix Z.

Scope: local

Returned as: an LLD_Z by (at least) LOCq(N_Z) array, containing numbers of the data type indicated in Table 96.

work

is the work area used by this subroutine if lwork <> 0,where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, containing numbers of the data type indicated in Table 96, where:

If lwork >= 1 or lwork = -1, then:

If jobz = 'N', then work₁ is set to the minimum lwork value needed.
If jobz = 'V', then work₁ is set to the minimum lwork value needed to compute all eigenvectors, but not necessarily sufficient to guarantee orthogonality of the eigenvectors. Except for work₁, the contents of work are overwritten on return.

iwork

is the work area used by this subroutine if liwork <> 0, where:

If liwork <> 0 and liwork <> -1, then its size is (at least) of length liwork.

If liwork = -1, then its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If liwork >= 1 or liwork = -1, then iwork₁ is set to the minimum liwork value and contains numbers of the data type indicated in Table 96. Except for iwork₁, the contents of iwork are overwritten on return.

ifail

has the following meaning:

If jobz = 'N', then ifail is ignored.

If jobz = 'V', it is vector ifail, where:

If there is a normal exit (see info), the first m elements of ifail are zero.
If there is an error exit (where one or more eigenvectors failed to converge--see info), ifail contains the indices of the eigenvectors that failed to converge.

Scope: global

Returned as: a one-dimensional array of (at least) length n, containing fullword integers; 0 <= ifail_i <= n.

iclustr

has the following meaning:

If jobz = 'N', then iclustr is ignored.

If jobz = 'V', it is vector iclustr, containing the indices of the eigenvectors corresponding to a cluster of eigenvalues that could not be reorthogonalized due to insufficient workspace. Eigenvectors corresponding to clusters of eigenvalues indexed iclustr_2i-1 to iclustr_2i could not be reorthogonalized due to lack of workspace. Hence, the eigenvectors corresponding to these clusters may not be orthogonal.

iclustr is a zero-terminated vector; that is, the last element of iclustr is set to zero. Assuming that k is the number of clusters, then:

iclustr_2k <> 0 and iclustr_2k+1 = 0

Scope: global

Returned as: a one-dimensional array of (at least) length 2(nprow)(npcol), containing fullword integers; 0 <= iclustr_i <= n.

gap

has the following meaning:

If jobz = 'N', then gap is ignored.

If jobz = 'V', it is vector gap, containing the gap between the eigenvalues whose eigenvectors could not be reorthogonalized. The values in this vector correspond to the clusters indicated by iclustr. As a result, the dot product between the eigenvectors corresponding to the i-th cluster may be as high as (C)(n)/gap_i, where C is a small constant.

Scope: global

Returned as: a one-dimensional array of (at least) length (nprow)(npcol), containing numbers of the data type indicated in Table 96.

info

has the following meaning:

If info = 0, then no input-argument errors or computational errors occurred. This indicates a normal exit.
Note: One use of info in ScaLAPACK is to identify whether input-argument errors occurred. Because Parallel ESSL terminates the application if input-argument errors occur, the setting of info is irrelevant for these errors.

If info > 0, then one or more of the following computational errors occurred and the appropriate error messages were issued, indicating an error exit, where:

If mod(info, 2) <> 0, then one or more eigenvectors failed to converge. Their indices are stored in ifail. (Ensure that abstol = (2)(unfl).)
If mod(info/2, 2) <> 0, then the eigenvectors corresponding to one or more clusters of eigenvalues could not be reorthogonalized because of insufficient workspace. The indices of the clusters are stored in iclustr.
If mod(info/4, 2) <> 0, then all the eigenvectors between vl and vu could not be computed because of insufficient space. The number of eigenvectors computed is returned in nz.
If mod(info/8, 2) <> 0, then one of more eigenvalues were not computed. (Ensure that abstol = (2)(unfl).)

Scope: global

Returned as: a fullword integer; info >= 0.

Notes and Coding Rules

This subroutine accepts lowercase letters for the jobz, range, and uplo arguments.
In your C program, argument info must be passed by reference.
A, Z, w, ifail, iclustr, gap, work, and iwork must have no common elements; otherwise, results are unpredictable.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
The global symmetric matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
The global symmetric matrix A must be aligned on a block boundary; that is:
- ia-1 must be a multiple of MB_A
- ja-1 must be a multiple of NB_A
If jobz = 'V', then also follow these rules:
- In the process grid, the process row containing the first row of the submatrix A must also contain the first row of the submatrix Z; that is: iarow = izrow
  where:
  - iarow = mod(RSRC_A+(ia-1)/MB_A, p)
  - izrow = mod(RSRC_Z+(iz-1)/MB_Z, p)
- M_A = M_Z
- MB_A = MB_Z
- NB_A = NB_Z
- RSRC_A = RSRC_Z
- CSRC_A = CSRC_Z
- CTXT_A = CTXT_Z
- The block row offset of the global symmetric matrix A must be equal to the block row offset of the global general matrix Z; that is:
  - mod((ia-1, MB_A) = mod(iz-1, MB_Z))
Eigenvectors associated with tightly clustered eigenvalues may not be orthogonal.
Eigenvectors that are on different processes are not reorthogonalized. For details, see the lwork argument.
An example of the use of this subroutine in a thermal diffusion application program is shown in Appendix B. "Sample Programs". See "Program Main (Message Passing)".
If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.
If liwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

This subroutine computes selected eigenvalues and, optionally, the eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying a range of values or a range of indices for the eigenvalues. The computation involves the following steps:

Reduce the real symmetric matrix A to real symmetric tridiagonal form.
Compute the requested eigenvalues of the real symmetric tridiagonal matrix using bisection.
If requested, compute the eigenvectors of the real symmetric tridiagonal matrix using inverse iteration, and then back transform the eigenvectors to obtain the eigenvectors of the real symmetric matrix A.

Error Conditions

Computational Errors

Note:

For more details, see output argument info.

Bisection failed to converge for some eigenvalues. The eigenvalues may not be as accurate as the absolute and relative tolerances.
The number of eigenvalues computed does not match the number of eigenvalues requested.
No eigenvalues were computed, because the Gershgorin interval initially used was incorrect.
Some eigenvectors failed to converge. The indices are stored in ifail.
Eigenvectors corresponding to one or more clusters of eigenvalues could not be reorthogonalized because of insufficient workspace. The indices of the clusters are stored in iclustr.
All the eigenvectors between vl and vu could not be computed due to insufficient workspace. The number of eigenvectors computed is returned in nz.

Resource Errors

(lwork = 0 or liwork = 0) and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1

DTYPE_A is invalid.
DTYPE_Z is invalid and jobz = 'V'

Stage 2

CTXT_A is invalid.

Stage 3

PDSYEVX has been called from outside the process grid.

Stage 4

jobz <> 'N' or 'V'
range <> 'U', 'V', or 'I'
uplo <> 'U' or 'L'
n < 0
M_A < 0 and n = 0; M_A < 1 otherwise
N_A < 0 and n = 0; N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1

If jobz = 'V':
M_Z < 0 and n = 0; M_Z < 1 otherwise
N_Z < 0 and n = 0; N_Z < 1 otherwise
MB_Z < 1
NB_Z < 1
RSRC_Z < 0 or RSRC_Z >= p
CSRC_Z < 0 or CSRC_Z >= q
iz < 1
jz < 1
CTXT_A <> CTXT_Z

Stage 5

vu <= vl and range = 'V' and n <> 0
il < 1 and range = 'I'
(iu < min(n, il) or iu > n) and range = 'I'

If n <> 0:
ia > M_A
ja > N_A
ia+n-1 > M_A
ja+n-1 > N_A

If n <> 0 and jobz = 'V':
iz > M_Z
jz > N_Z
iz+n-1 > M_Z
jz+n-1 > N_Z

In all cases:
MB_A <> NB_A
mod(ia-1, MB_A) <> 0
mod(ja-1, NB_A) <> 0

If jobz = 'V':
M_A <> M_Z
MB_A <> MB_Z
NB_A <> NB_Z
mod(iz-1, MB_Z) <> mod(ia-1, MB_A)
In the process grid, the process row containing the first row of the submatrix A does not contain the first row of the submatrix Z; that is, iarow <> izrow, where:
1. iarow = mod(RSRC_A + (ia-1)/MB_A, p)
2. izrow = mod(RSRC_Z + (iz-1)/MB_Z, p)
RSRC_A <> RSRC_Z
CSRC_A <> CSRC_Z

Stage 6

LLD_A < max(1, LOCp(M_A))
lwork <> 0, lwork <> -1, and lwork < (minimum value). (For the minimum value, see the lwork argument description.)
liwork <> 0, liwork <> -1, and liwork < (minimum value). (For the minimum value, see the liwork argument description.)

If jobz = 'V':
LLD_Z < max(1, LOCp(M_Z))

Stage 7

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

jobz differs.
range differs.
uplo differs.
n differs.
ia differs.
ja differs.
DTYPE_A differs.
M_A differs.
N_A differs.
MB_A differs.
NB_A differs.
RSRC_A differs.
CSRC_A differs.
ABSTOL differs.

Also:
lwork = -1 on a subset of processes.
liwork = -1 on a subset of processes.

Stage 8

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

If range = 'V':

vl differs.
vu differs.

If range = 'I':
il differs.
iu differs.

If jobz = 'V':
iz differs.
jz differs.
DTYPE_Z differs.
M_Z differs.
N_Z differs.
MB_Z differs.
NB_Z differs.
RSRC_Z differs.
CSRC_Z differs.
ORFAC differs.

Example

This example shows how to find all the eigenvalues and eigenvectors of a real symmetric matrix A of order 4 using a 2 × 2 process grid.

Notes:

Because range = 'A', arguments vl, vu, il, and iu are not referenced.
Because lwork = 0 and liwork = 0, PDSYEVX dynamically allocates the work areas used by this subroutine.

Call Statements and Input

 ORDER = 'R'
 NPROW = 2
 NPCOL = 2
 CALL BLACS_GET(0, 0, ICONTXT)
 CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
 CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
               JOBZ RANGE UPLO  N  A IA JA  DESC_A   VL     VU   IL IU  ABSTOL  M  NZ  W
                |     |     |   |  |  |  |    |       |      |    |  |     |    |   |  |
 CALL PDSYEVX( 'V',  'A',  'U', 4, A, 1, 1, DESC_A, 0.0D0, 0.0D0, 0, 0, -1.0D0, M, NZ, W,
 
               ORFAC  Z IZ JZ  DESC_Z  WORK LWORK IWORK LIWORK IFAIL  ICLUSTR  GAP  INFO
+           |    |  |  |    |      |     |     |      |     |       |      |    |
              -1.0D0, Z, 1, 1, DESC_Z, WORK , 0 , IWORK ,  0 , IFAIL, ICLUSTR, GAP, INFO)

DESC_A

DESC_Z

DTYPE_

CTXT_

icontxt¹

MB_

NB_

RSRC_

CSRC_

LLD_

See below²

¹ icontxt is the output of the BLACS_GRIDINIT call.

² Each process should set the LLD_ as follows:

LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
LLD_Z = MAX(1,NUMROC(M_Z, MB_Z, MYROW, RSRC_Z, NPROW))

In this example, LLD_A = LLD_Z = 2 on all processes.

Global symmetric matrix A of order 4 with block sizes 1 × 1:

B,D     0        1        2        3
     *                                 *
 0   |  5.0  |   4.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 1   |   .   |   5.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 2   |   .   |    .   |   4.0  |   2.0 |
     | ------|--------|--------|------ |
 3   |   .   |    .   |    .   |   4.0 |
     *                                 *

The following is the 2 × 2 process grid:

B,D 0 2 1 3
0
2
P₀₀ P₀₁
1
3
P₁₀ P₁₁

B,D	0 2	1 3
0 2	P₀₀	P₀₁
1 3	P₁₀	P₁₁

Local arrays for A:

p,q  |     0      |      1
-----|------------|------------
 0   |  5.0  1.0  |   4.0  1.0
     |   .   4.0  |    .   2.0
-----|------------|------------
 1   |   .   1.0  |   5.0  1.0
     |   .    .   |    .   4.0

Output:

The upper triangle, including the diagonal, of the global symmetric matrix A is overwritten; that is, the original input is not preserved.

On all processes, m = 4 and nz = 4.

Global vector w of length 4 is the same on all processes:

w = (1.00, 2.00, 5.00, 10.00)

Global general matrix Z of order 4 with block sizes 1 × 1:

B,D       0           1           2           3
     *                                             *
 0   |  0.7071  |   0.0000  |  -0.3162  |  -0.6325 |
     | ---------|-----------|-----------|--------- |
 1   | -0.7071  |   0.0000  |  -0.3162  |  -0.6325 |
     | ---------|-----------|-----------|--------- |
 2   |  0.0000  |  -0.7071  |   0.6325  |  -0.3162 |
     | ---------|-----------|-----------|--------- |
 3   |  0.0000  |   0.7071  |   0.6325  |  -0.3162 |
     *                                             *

The following is the 2 × 2 process grid:

B,D 0 2 1 3
0
2
P₀₀ P₀₁
1
3
P₁₀ P₁₁

B,D	0 2	1 3
0 2	P₀₀	P₀₁
1 3	P₁₀	P₁₁

Local arrays for Z:

p,q  |        0          |         1
-----|-------------------|-------------------
 0   |  0.7071  -0.3162  |   0.0000  -0.6325
     |  0.0000   0.6325  |  -0.7071  -0.3162
-----|-------------------|-------------------
 1   | -0.7071  -0.3162  |   0.0000  -0.6325
     |  0.0000   0.6325  |   0.7071  -0.3162

Global vector ifail of length 4 is the same on all processes:

ifail = (0, 0, 0, 0)

Global vector iclustr of length 8 ( = 2(nprow)(npcol)) is the same on all processes:

iclustr = (0, 0, 0, 0, 0, 0, 0, 0)

Global vector gap of length 4 ( = (nprow)(npcol)) is the same on all processes:

gap = (-1.0, -1.0, -1.0, -1.0)

The value of info is 0 on all processes.

PDSYTRD--Reduce a Real Symmetric Matrix to Tridiagonal Form

This subroutine reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

where A represents the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1}.

If n = 0, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13] and [21].

Table 97. Data Types

A, d, e, tau, work Subroutine
Long-precision real PDSYTRD

Syntax

Fortran	CALL PDSYTRD (`uplo`, `n`, `a`, `ia`, `ja`, `desc_a`, `d`, `e`, `tau`, `work`, `lwork`, `info`)
C and C++	pdsytrd (`uplo`, `n`, `a`, `ia`, `ja`, `desc_a`, `d`, `e`, `tau`, `work`, `lwork`, `info`);

On Entry

uplo

indicates whether the upper or lower triangular part of the global symmetric submatrix A is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Scope: global

Specified as: a single character; uplo = 'U' or 'L'.

n

is the order of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

a

If uplo = 'U', the leading n × n upper triangular part of the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1} must contain the upper triangular part of the symmetric matrix, and the strictly lower triangular part is not referenced.
If uplo = 'L', the leading n × n lower triangular part of the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1} must contain the lower triangular part of the symmetric matrix, and the strictly upper triangular part is not referenced.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 97. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+n-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `n` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `n` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

d

See 'On Return'.

e

See 'On Return'.

tau

See 'On Return'.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is the work area used by this subroutine, where:

If lwork <> -1, its size is (at least) of length lwork.
If lwork = -1, its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 97.

lwork

is the number of elements in array WORK.

Scope:

If lwork >= 0, lwork is local
If lwork = -1, lwork is global

Specified as: a fullword integer; where:

If lwork = 0, PDSYTRD dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If lwork = -1, PDSYTRD performs a work area query and returns the minimum size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, it must have the following value:
lwork >= max(nb(np+1), 3nb)
where:

nb = MB_A = NB_A
iarow = mod(RSRC_A+(ia-1)/nb, nprow).
np = NUMROC(n, nb, myrow, iarow, nprow)

info

See 'On Return'.

On Return

a

is the updated local part of the global symmetric matrix A, containing the results of the computation, where:

If uplo = 'U', the diagonal and first superdiagonal of A_{ia:ia+n-1,
ja:ja+n-1} are overwritten by the corresponding elements of the tridiagonal matrix T. The elements above the first superdiagonal are overwritten with v_1:i-1. These elements with tau represent the orthogonal matrix Q as a product of of elementary reflectors.
If uplo = 'L', the diagonal and first subdiagonal of A_{ia:ia+n-1,
ja:ja+n-1} are overwritten by the corresponding elements of the tridiagonal matrix T. The elements below the first subdiagonal are overwritten with v_i+2:n. These elements with tau represent the orthogonal matrix Q as a product of elementary reflectors.

See "Function", for more information.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 97. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

d

is the updated local part of the global matrix D, where d_ja:ja+n-1 contains the diagonal elements of the tridiagonal matrix T.

This identifies the first element of the local array D. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array D must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix D.

A copy of the vector d, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of d is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 97.

e

is the updated local part of the global matrix E, containing the off-diagonal elements of the tridiagonal matrix T, where:

If uplo = 'U', then e_ja = 0 and e_ja+1:ja+n-1 contains the superdiagonal elements of the tridiagonal matrix T.

If uplo = 'L', then e_ja:ja+n-2 contains the subdiagonal elements of the tridiagonal matrix T, and e_ja+n-1 = 0.

This identifies the first element of the local array E. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array E must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix E.

A copy of the vector e, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of E is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 97.

tau

is the updated local part of the global matrix tau, containing the scalar factors of the elementary reflectors, where:

If uplo = 'U', then tau_ja = 0 and tau_ja+1:ja+n-1 contains the scalar factors of the elementary reflectors.

If uplo = 'L', then tau_ja:ja+n-2 contains the scalar factors of the elementary reflectors and tau_ja+n-1 = 0

This identifies the first element of the local array tau. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array tau must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix tau.

A copy of the vector tau, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of tau is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 97.

work

is the work area used by this subroutine if lwork <> 0, where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If lwork >= 1 or lwork = -1, then work₁ is set to the minimum lwork value and contains numbers of the data type indicated in Table 97. Except for work₁, the contents of work are overwritten on return.

info

indicates that a successful computation occurred.

Scope: global

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

This subroutine accepts lowercase letters for the uplo argument.
In your C program, argument info must be passed by reference.
Matrix A, d, e, tau, and work must have no common elements; otherwise, results are unpredictable.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
The global symmetric matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
The global symmetric matrix A must be aligned on a block boundary; that is:
- ia-1 must be a multiple of MB_A
- ja-1 must be a multiple of NB_A
There are no array descriptors for d, e, and tau. These are all row distributed vectors with block size NB_A, local arrays of dimension 1 by LOCq(N_A), and global index ja. A copy of these vectors exist on each row of the process grid, and the process column over which the first column of D, E, and tau is distributed is CSRC_A.
For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

This subroutine reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

where:

A represents the global symmetric submatrix A_{ia:ia+n-1,
ja:ja+n-1}.
Matrix Q represents the following:
- For uplo = 'U', the matrix Q is the product of elementary reflectors: Q = H_n-1 ... H₂ H₁,
  where:
  
  For each i: H_i = I-tauvv^T
  tau is a real scalar
  v is a real vector with v_i+1:n = 0 and v_i = 1
  v_1:i-1 is stored on return in submatrix A_{1+(ia-1):i-1+(ia-1),
  i+1+(ja-1)}
  tau is stored on return in tau_i+(ja-1)
  I is the identity matrix
  
  If uplo = 'U', then the following example shows the contents of A on return with n = 5 and ia = ja = 1:
  
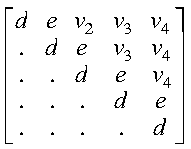
  where:
  
  d represents the diagonal elements of T
  e represents the superdiagonal elements of T
  v_i represents the corresponding elements of the vector defining H_i.
- For uplo = 'L', the matrix Q is the product of elementary reflectors: Q = H₁H₂ ... H_n-1,
  
  where:
  
  For each i: H_i = I-tauvv^T
  tau is a real scalar
  v is a real vector with v_1:i = 0 and v_i+1 = 1.
  v_i+2:n is stored on return in submatrix A_{i+2+(ia-1):n+(ia-1),
  i+(ja-1)}.
  tau is stored on return in tau_i+(ja-1)
  I is the identity matrix.
  
  If uplo = 'L', then the following example shows the contents of A on return with n = 5 and ia = ij = 1:
  
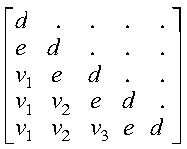
  where:
  
  d represents the diagonal elements of T
  e represents the subdiagonal elements of T
  v_i represents the corresponding elements of the vector defining H_i.

Error Conditions

Computational Errors

None

Resource Errors

lwork = 0 and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1

DTYPE_A is invalid.

Stage 2

CTXT_A is invalid.

Stage 3

PDSYTRD has been called from outside the process grid.

Stage 4

uplo <> 'U' or 'L'
n < 0
M_A < 0 and n = 0; M_A < 1 otherwise
N_A < 0 and n = 0; N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1

Stage 5

If n <> 0:

ia > M_A
ja > N_A
ia+n-1 > M_A
ja+n-1 > N_A

In all cases:

MB_A <> NB_A
mod(ia-1, MB_A) <> 0
mod(ja-1, NB_A) <> 0

Stage 6

LLD_A < max(1, LOCp(M_A))
lwork <> 0, lwork <> -1, and lwork < max(nb(np+1), 3nb)
where:

nb = MB_A = NB_A
iarow = mod(RSRC_A+(ia-1)/nb, nprow).
np = NUMROC(n, nb, myrow, iarow, nprow)

Stage 7

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

uplo differs.
n differs.
ia differs.
ja differs.
DTYPE_A differs.
M_A differs.
N_A differs.
MB_A differs.
NB_A differs.
RSRC_A differs.
CSRC_A differs.

Also:
lwork = -1 on a subset of processes.

Example

This example shows the reduction of a symmetric matrix of order 4 to symmetric tridiagonal form, using a 2 × 2 process grid.
Note: Because lwork = 0, PDSYTRD dynamically allocates the work area used by this subroutine.

Call Statements and Input

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO  N   A   IA  JA   DESC_A   D   E   TAU   WORK  LWORK   INFO
               |    |   |    |   |     |      |   |    |     |      |      |
CALL PDSYTRD( 'U' , 4 , A  , 1 , 1 , DESC_A , D , E , TAU , WORK ,  0   , INFO )

DESC_A

DTYPE_

CTXT_

icontxt¹

MB_

NB_

RSRC_

CSRC_

LLD_

See below²

¹ icontxt is the output of the BLACS_GRIDINIT call.

² Each process should set the LLD_ as follows:

LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))

In this example, LLD_A = 2 on all processes.

Global symmetric matrix A of order 4 with block sizes 1 × 1:

B,D     0        1        2        3
     *                                 *
 0   |  5.0  |   4.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 1   |   .   |   5.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 2   |   .   |    .   |   4.0  |   2.0 |
     | ------|--------|--------|------ |
 3   |   .   |    .   |    .   |   4.0 |
     *                                 *

The following is the 2 × 2 process grid:

B,D 0 2 1 3
0
2
P₀₀ P₀₁
1
3
P₁₀ P₁₁

B,D	0 2	1 3
0 2	P₀₀	P₀₁
1 3	P₁₀	P₁₁

Local arrays for A:

p,q  |     0      |      1
-----|------------|------------
 0   |  5.0  1.0  |   4.0  1.0
     |   .   4.0  |    .   2.0
-----|------------|------------
 1   |   .   1.0  |   5.0  1.0
     |   .    .   |    .   4.0

Output:

Global symmetric matrix A of order 4 with block sizes 1 × 1:

B,D      0         1         2         3
     *                                     *
 0   |  1.00  |   0.00  |   0.41  |   0.22 |
     | -------|---------|---------|------- |
 1   |   .    |   6.00  |   2.83  |   0.22 |
     | -------|---------|---------|------- |
 2   |   .    |    .    |   7.00  |  -2.45 |
     | -------|---------|---------|------- |
 3   |   .    |    .    |    .    |   4.00 |
     *                                     *

The following is the 2 × 2 process grid:

B,D 0 2 1 3
0
2
P₀₀ P₀₁
1
3
P₁₀ P₁₁

B,D	0 2	1 3
0 2	P₀₀	P₀₁
1 3	P₁₀	P₁₁

Local arrays for A:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  1.00  0.41  |   0.00  0.22
     |   .    7.00  |    .   -2.45
-----|--------------|--------------
 1   |   .    2.83  |   6.00  0.22
     |   .     .    |    .    4.00

Global row vector D of length 4 with block sizes 1 × 1:

B,D      0         1         2         3
     *                                     *
 0   |  1.00  |   6.00  |   7.00  |   4.00 |
     *                                     *

Note:

A copy of D is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 2 1 3

P₀₀ P₀₁

P₁₀ P₁₁

B,D	0 2	1 3
	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for D:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  1.00  7.00  |   6.00  4.00
-----|--------------|--------------
 1   |  1.00  7.00  |   6.00  4.00

Global row vector E of length 4 with block sizes 1 × 1:

B,D      0         1         2         3
     *                                     *
 0   |  0.00  |   0.00  |   2.83  |  -2.45 |
     *                                     *

Note:

A copy of E is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 2 1 3

P₀₀ P₀₁

P₁₀ P₁₁

B,D	0 2	1 3
	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for E:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  0.00  2.83  |   0.00 -2.45
-----|--------------|--------------
 1   |  0.00  2.83  |   0.00 -2.45

Global row vector tau of length 4 with block sizes 1 × 1:

B,D      0         1         2         3
     *                                     *
 0   |  0.00  |   0.00  |   1.71  |   1.82 |
     *                                     *

Note:

A copy of tau is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 2 1 3

P₀₀ P₀₁

P₁₀ P₁₁

B,D	0 2	1 3
	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for tau:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  0.00  1.71  |   0.00  1.82
-----|--------------|--------------
 1   |  0.00  1.71  |   0.00  1.82

The value of info is 0 on all processes.

PDGEHRD--Reduce a General Matrix to Upper Hessenberg Form

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where A represents the global general submatrix A_{ia+ilo-1:
ia+ihi-1, ja+ilo-1:
ja+ihi-1}.

If n = 0, no computation is performed, and the subroutine returns after doing some parameter checking. Then, if ihi = ilo, the subroutine returns after doing some parameter checking and setting tau_ja:ja+ilo-2 and tau_{ja+ihi-1:ja+n-2} to zero.

See references [13] and [21].

Table 98. Data Types

A, tau, work Subroutine
Long-precision real PDGEHRD

Syntax

Fortran	CALL PDGEHRD (`n`, `ilo`, `ihi`, `a`, `ia`, `ja`, `desc_a`, `tau`, `work`, `lwork`, `info`)
C and C++	pdgehrd (`n`, `ilo`, `ihi`, `a`, `ia`, `ja`, `desc_a`, `tau`, `work`, `lwork`, `info`);

On Entry

n

is the order of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

ilo

lower range of the rows or columns in the global general submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; 1 <= ilo <= max(1, n).

ihi

upper range of the rows or columns in the global general submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; min(ilo, n) <= ihi <= n.

a

is the local part of the global general matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+n-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+n-1 by ja+n-1 part of the global matrix.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 98. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+n-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `n` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `n` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

tau

See 'On Return'.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is the work area used by this subroutine, where:

If lwork <> -1, its size is (at least) of length lwork.
If lwork = -1, its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 98.

lwork

is the number of elements in array WORK.

Scope:

If lwork >= 0, lwork is local
If lwork = -1, lwork is global

Specified as: a fullword integer; where:

If lwork = 0, PDGEHRD dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If lwork = -1, PDGEHRD performs a work area query and returns the minimum size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, it must have the following value:
lwork >= (nb × nb)+nb × max(ihip+1, ihlp+inlq)
where:

nb = MB_A = NB_A
ioff = mod(ia+ilo-2, nb)
iroffa = mod(ia-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow)
ilrow = mod(RSRC_A+(ia+ilo-2)/nb, nprow)
ilcol = mod(CSRC_A+(ja+ilo-2)/nb, npcol)
ihip = NUMROC(ihi+iroffa, nb, myrow, iarow, nprow)
ihlp = NUMROC(ihi-ilo+ioff+1, nb, myrow, ilrow, nprow)
inlq = NUMROC(n-ilo+ioff+1, nb, mycol, ilcol, npcol)

info

See 'On Return'.

On Return

a

is the updated local part of the global general matrix A, containing the results of the computation.

The upper triangle and the first subdiagonal of A_{ia:ia+n-1,
ja:ja+n-1} are overwritten by the corresponding elements of the upper Hessenberg matrix H. The elements below the first subdiagonal are overwritten with v_i+2:ihi. These elements with tau represent the orthogonal matrix Q as a product of elementary reflectors.

See "Function", for more information.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 98. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

tau

is the updated local part of the global matrix tau, where:

tau_{ja+ilo-1:ja+ihi-2} contains the scalar factors of the elementary reflectors.
tau_ja:ja+ilo-2 are set to zero.
tau_{ja+ihi-1:ja+n-2} are set to zero.

This identifies the first element of the local array tau. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-2) part of the local array tau must contain the local pieces of the leading 1 by ja+n-2 part of the global matrix tau.

A copy of the vector tau, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of tau is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A-1) array, containing numbers of the data type indicated in Table 98.

work

is the work area used by this subroutine if lwork <> 0, where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If lwork >= 1 or lwork = -1, then work₁ is set to the minimum lwork value and contains numbers of the data type indicated in Table 98. Except for work₁, the contents of work are overwritten on return.

info

indicates that a successful computation occurred.

Scope: global

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

In your C program, argument info must be passed by reference.
Matrix A, tau, and work must have no common elements; otherwise, results are unpredictable.
On entry, the general submatrix A_{ia:ia+n-1,
ja:ja+n-1} must already be upper triangular in rows (ia:ia+ilo-2) and (ia+ihi:ia+n-1), and upper triangular in columns (ja:ja+ilo-2) and (ja+ihi:ja+n-1). If this is not the case, you should set ilo = 1 and ihi = n.
If n = 0, you should set ilo = 1 and ihi = 0. If n > 0, you should set 1 <= ilo <= ihi <= n.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
The global general matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
The global general matrix A must be aligned on a block boundary; that is:
- ia-1 must be a multiple of MB_A
- ja-1 must be a multiple of NB_A
There is no array descriptor for tau. tau is a row-distributed vector with block size NB_A, local arrays of dimension 1 by LOCq(N_A-1), and global index ja. A copy of tau exists on each row of the process grid, and the process column over which the first column of tau is distributed is CSRC_A.
For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where:

A represents the global general submatrix A_{ia+ilo-1:ia+ihi-1,
ja+ilo-1:ja+ihi-1}
Matrix Q is represented as a product of (ihi-ilo) elementary reflectors:

Q = H_ilo H_ilo+1 ... H_ihi-1

where:

For each i: H_i = I-tauvv^T
tau is a real scalar
v is a real vector with v_1:i = 0, v_i+1 = 1, and v_ihi+1:n = 0
v_i+2:ihi is stored on return in in submatrix A_{i+ilo+1+(ia-1):ihi+(ia-1),
ilo+i-1+(ja-1)}
tau is stored on return in tau_{i+ilo-1+(ja-1)}
I is the identity matrix

The following example shows the contents of the general submatrix A on entry with n = 7, ia = ja = 1, ilo = 2, and ihi = 6:

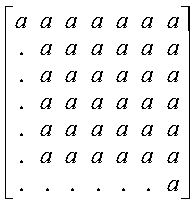
Following is the general submatrix A on return:

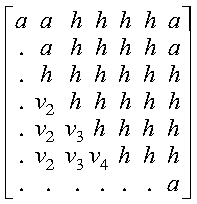
where:

a represents an element of the original submatrix A.
h represents a updated element of the upper Hessenberg matrix H.
v_i represents the corresponding elements of the vector defining H_{ilo+i-1+(ja-1)}.

Error Conditions

Computational Errors

None

Resource Errors

lwork = 0 and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1

DTYPE_A is invalid.

Stage 2

CTXT_A is invalid.

Stage 3

PDGEHRD has been called from outside the process grid.

Stage 4

n < 0
M_A < 0 and n = 0; M_A < 1 otherwise
N_A < 0 and n = 0; N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1

Stage 5

ilo < 1 or ilo > max(1, n)
ihi < min(ilo, n) or ihi > n

If n <> 0:

ia > M_A
ja > N_A
ia+n-1 > M_A
ja+n-1 > N_A

In all cases:

MB_A <> NB_A
mod(ia-1, MB_A) <> 0
mod(ja-1, NB_A) <> 0

Stage 6

LLD_A < max(1, LOCp(M_A))
lwork <> 0, lwork <> -1, and lwork < (nb × nb)+nb × max(ihip+1, ihlp+inlq)
where:

nb = MB_A = NB_A
ioff = mod(ia+ilo-2, nb)
iroffa = mod(ia-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow)
ilrow = mod(RSRC_A+(ia+ilo-2)/nb, nprow)
ilcol = mod(CSRC_A+(ja+ilo-2)/nb, npcol)
ihip = NUMROC(ihi+iroffa, nb, myrow, iarow, nprow)
ihlp = NUMROC(ihi-ilo+ioff+1, nb, myrow, ilrow, nprow)
inlq = NUMROC(n-ilo+ioff+1, nb, mycol, ilcol, npcol)

Stage 7

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

n differs.
ilo differs.
ihi differs.
ia differs.
ja differs.
DTYPE_A differs.
M_A differs.
N_A differs.
MB_A differs.
NB_A differs.
RSRC_A differs.
CSRC_A differs.

Also:
lwork = -1 on a subset of processes.

Example

This example shows the reduction of a general matrix of order 3 to upper Hessenberg form using a 2 × 2 process grid.
Note: Because lwork = 0, PDGEHRD dynamically allocates the work area used by this subroutine.

Call Statements and Input

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              N   ILO   IHI   A  IA  JA   DESC_A   TAU   WORK   LWORK   INFO
              |    |     |    |   |   |     |       |     |       |      |
CALL PDGEHRD( 3 ,  1  ,  3  , A , 1 , 1 , DESC_A , TAU , WORK  ,  0   , INFO)

DESC_A

DTYPE_

CTXT_

icontxt¹

MB_

NB_

RSRC_

CSRC_

LLD_

See below²

¹ icontxt is the output of the BLACS_GRIDINIT call.

² Each process should set the LLD_ as follows:

LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))

In this example, LLD_A = 2 on P₀₀ and P₀₁, and LLD_A = 1 on P₁₀ and P₁₁.

Global general matrix A of order 3 with block sizes 1 × 1:

B,D      0         1         2
     *                           *
 0   |  33.0  |   16.0  |   72.0 |
     | -------|---------|------- |
 1   | -24.0  |  -10.0  |  -57.0 |
     | -------|---------|------- |
 2   |  -8.0  |   -4.0  |  -17.0 |
     *                           *

The following is the 2 × 2 process grid:

B,D 0 2 1
0
2
P₀₀ P₀₁
1 P₁₀ P₁₁

B,D	0 2	1
0 2	P₀₀	P₀₁
1	P₁₀	P₁₁

Local arrays for A:

p,q  |      0       |    1
-----|--------------|--------
 0   |  33.0  72.0  |   16.0
     |  -8.0 -17.0  |   -4.0
-----|--------------|--------
 1   | -24.0 -57.0  |  -10.0

Output:

Global general matrix A of order 3 with block sizes 1 × 1:

B,D      0          1          2
     *                              *
 0   |  33.00  |  -37.95  |   63.25 |
     | --------|----------|-------- |
 1   |  25.30  |  -29.00  |   53.00 |
     | --------|----------|-------- |
 2   |   0.16  |    0.00  |    2.00 |
     *                              *

The following is the 2 × 2 process grid:

B,D 0 2 1
0
2
P₀₀ P₀₁
1 P₁₀ P₁₁

B,D	0 2	1
0 2	P₀₀	P₀₁
1	P₁₀	P₁₁

Local arrays for A:

p,q  |       0        |    1
-----|----------------|---------
 0   |  33.0   63.25  |  -37.95
     |   0.16   2.00  |    0.00
-----|----------------|---------
 1   |  25.30  53.00  |  -29.00

Global row vector tau of length 2 with block sizes of 1:

B,D      0         1
     *                 *
 0   |  1.95  |   0.00 |
     *                 *

Note:

A copy of tau is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 1

P₀₀ P₀₁

P₁₀ P₁₁

B,D	0	1
	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for tau:

p,q  |   0    |    1
-----|--------|--------
 0   |  1.95  |   0.00
-----|--------|--------
 1   |  1.95  |   0.00

The value of info is 0 on all processes.

PDGEBRD--Reduce a General Matrix to Bidiagonal Form

This subroutine reduces a real general matrix A of order m by n to upper or lower bidiagonal form B by an orthogonal transformation:

B = Q^TAP

where:

A represents the global general submatrix A_{ia:ia+m-1,
ja:ja+n-1}.
If m >= n, then B is upper bidiagonal.
If m < n, then B is lower bidiagonal.

If min(m, n) = 0, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13] and [21].

Table 99. Data Types

A, d, e, tau_q, tau_p, work Subroutine
Long-precision real PDGEBRD

Syntax

Fortran	CALL PDGEBRD (`m`, `n`, `a`, `ia`, `ja`, `desc_a`, `d`, `e`, `tauq`, `taup`, `work`, `lwork`, `info`)
C and C++	pdgebrd (`m`, `n`, `a`, `ia`, `ja`, `desc_a`, `d`, `e`, `tauq`, `taup`, `work`, `lwork`, `info`);

On Entry

m

is the number of rows of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; m >= 0

n

is the number of columns of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

a

is the local part of the global general matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+m-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+m-1 by ja+n-1 part of the global matrix.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 99. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+m-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `m` = 0 or `n` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `m` = 0 or `n` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

d

See 'On Return'.

e

See 'On Return'.

tauq

See 'On Return'.

taup

See 'On Return'.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is the work area used by this subroutine, where:

If lwork <> -1, its size is (at least) of length lwork.
If lwork = -1, its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 99.

lwork

is the number of elements in array WORK.

Scope:

If lwork >= 0, lwork is local
If lwork = -1, lwork is global

Specified as: a fullword integer; where:

If lwork = 0, PDGEBRD dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If lwork = -1, PDGEBRD performs a work area query and return the minimum size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, it must have the following value:
lwork >= nb(mp0+nq0+1)+nq0
where:

nb = MB_A = NB_A
iroffa = mod(ia-1, nb)
icoffa = mod(ja-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow).
iacol = mod(CSRC_A+(ja-1)/nb, npcol).
mp0 = NUMROC(m+iroffa, nb, myrow, iarow, nprow)
nq0 = NUMROC(n+icoffa, nb, mycol, iacol, npcol)

info

See 'On Return'.

On Return

a

is the updated local part of the global general matrix A, containing the results of the computation, where:

If m >= n, the diagonal and first superdiagonal of A_{ia:ia+m-1,
ja:ja+n-1} are overwritten by the corresponding elements of the upper bidiagonal matrix B. The elements below the diagonal are overwritten with v_i+1:m. These elements with tau_q represent the orthogonal matrix Q as a product of of elementary reflectors. The elements above the first superdiagonal are overwritten with u_i+2:n. These elements with tau_p represent the orthogonal matrix P as a product of of elementary reflectors.
If m < n, the diagonal and first subdiagonal of A_{ia:ia+m-1,
ja:ja+n-1} are overwritten by the corresponding elements of the lower bidiagonal matrix B. The elements below the first subdiagonal are overwritten with v_i+2:m. These elements with tau_q represent the orthogonal matrix Q as a product of elementary reflectors. The elements above the diagonal are overwritten with u_i+1:n. These elements with tau_p represent the orthogonal matrix P as a product of elementary reflectors.

See "Function", for more information.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 99. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

d

is the updated local part of the global matrix D, where:

If m >= n, then d_ja:ja+n-1 contains the diagonal elements of the bidiagonal matrix B.
This identifies the first element of the local array D. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array D must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix D.
A copy of the vector d, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of d is distributed is CSRC_A.
If m < n, then d_ia:ia+m-1 contains the diagonal elements of the bidiagonal matrix B.
This identifies the first element of the local array D. This subroutine computes the location of the first element of the local subarray used, based on ia, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+m-1) by 1 part of the local array D must contain the local pieces of the leading ia+m-1 by 1 part of the global matrix D.
A copy of the vector d, with a block size of MB_A and global index ia, is returned to each column of the process grid. The process row over which the first row of d is distributed is RSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array if m >= n, and a LOCp(M_A) by 1 array if m < n, containing numbers of the data type indicated in Table 99.

e

is the updated local part of the global matrix E, where:

If m >= n, then e_ia:ia+n-2 contains the superdiagonal elements of the bidiagonal matrix B.
This identifies the first element of the local array E. This subroutine computes the location of the first element of the local subarray used, based on ia, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+n-2) by 1 part of the local array E must contain the local pieces of the leading ia+n-2 by 1 part of the global matrix E.
A copy of the vector e, with a block size of MB_A and global index ia, is returned to each column of the process grid. The process row over which the first row of e is distributed is RSRC_A.
If m < n, then e_ja:ja+m-2 contains the subdiagonal elements of the bidiagonal matrix B.
This identifies the first element of the local array D. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+m-2) part of the local array E must contain the local pieces of the leading 1 by ja+m-2 part of the global matrix E.
A copy of the vector e, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of e is distributed is CSRC_A.

Scope: local

Returned as: an (at least) LOCp(N_A-1) by 1 array if m >= n and a 1 by (at least) LOCq(M_A-1) array if m < n, containing numbers of the data type indicated in Table 99.

tauq

is the updated local part of the global matrix tau_q, where:

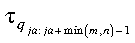
contains the scalar factors of the elementary reflectors which represent the orthogonal matrix Q. See "Function" for more details.

This identifies the first element of the local array tau_q. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+min(m, n)-1) part of the local array tau_q must contain the local pieces of the leading 1 by ja+min(m, n)-1 part of the global matrix tau_q.

A copy of the vector tau_q, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of tau_q is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(min(M_A, N_A)) array, containing numbers of the data type indicated in Table 99.

taup

is the updated local part of the global matrix tau_p, where:

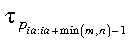
contains the scalar factors of the elementary reflectors which represent the orthogonal matrix P. See "Function" for more details.

This identifies the first element of the local array tau_p. This subroutine computes the location of the first element of the local subarray used, based on ia, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+min(m, n)-1) by 1 part of the local array tau_p must contain the local pieces of the leading ia+min(m, n)-1 by 1 part of the global matrix tau_p.

A copy of the vector tau_p, with a block size of MB_A and global index ia, is returned to each column of the process grid. The process row over which the first row of tau_p is distributed is RSRC_A.

Scope: local

Returned as: an (at least) LOCp(min(M_A, N_A)) by 1 array, containing numbers of the data type indicated in Table 99.

work

is the work area used by this subroutine if lwork <> 0, where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If lwork >= 1 or lwork = -1, then work₁ is set to the minimum lwork value and contains numbers of the data type indicated in Table 99. Except for work₁, the contents of work are overwritten on return.

info

indicates that a successful computation occurred.

Scope: global

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

In your C program, argument info must be passed by reference.
Matrix A, d, e, tau_q, tau_p, and work must have no common elements; otherwise, results are unpredictable.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
The global general matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
For the global general matrix A, the block row offset must be equal to the block column offset; that is, mod(ia-1, MB_A) = mod(ja-1, NB_A)
For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
There is no array descriptor for d, where:
- If m >= n, then d is a row-distributed vector with block size NB_A, local array of dimension 1 by LOCq(N_A), and global index ja. A copy of d exists on each row of the process grid, and the process column over which the first column of d is distributed is CSRC_A.
- If m < n, then d is a column-distributed vector with block size MB_A, local array of dimension LOCp(M_A) by 1, and global index ia. A copy of d exists on each column of the process grid, and the process row over which the first row of d is distributed is RSRC_A.
There is no array descriptor for e, where:
- If m >= n, then e is a column-distributed vector with block size MB_A, local array of dimension LOCp(N_A-1) by 1, and global index ia. A copy of e exists on each column of the process grid, and the process row over which the first row of e is distributed is RSRC_A.
- If m < n, then e is a row-distributed vector with block size NB_A, local array of dimension 1 by LOCq(M_A-1), and global index ja. A copy of e exists on each row of the process grid, and the process column over which the first column of e is distributed is CSRC_A.
There is no array descriptor for tau_q. tau_q is a row-distributed vector with block size NB_A, local array of dimension 1 by LOCq(min(M_A, N_A), and global index ja. A copy of tau_q exists on each row of the process grid, and the process column over which the first column of tau_q is distributed is CSRC_A.
There is no array descriptor for tau_p. tau_p is a column-distributed vector with block size MB_A, local array of dimension LOCp(min(M_A, N_A) by 1, and global index ia. A copy of tau_p exists on each column of the process grid, and the process row over which the first row of tau_p is distributed is RSRC_A.
If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

This subroutine reduces a real general matrix A of order m by n to upper or lower bidiagonal form B by an orthogonal transformation:

B = Q^TAP

where:

A represents the global general submatrix A_{ia:ia+m-1,
ja:ja+n-1}.
If m >= n, then B is upper bidiagonal, and matrices Q and P are represented as the product of elementary reflectors:

Q = H₁ H₂ ... H_n
P = G₁ G₂ ... G_n-1

where:

For each i: H_i = I-tau_qvv^T
For each i: G_i = I-tau_puu^T
tau_q is a real scalar and is stored on return in:

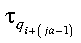
tau_p is a real scalar and is stored on return in:

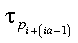
v is a real vector with v_1:i-1 = 0 and v_i = 1
v_i+1:m is stored on return in submatrix A_{i+1+(ia-1):m+(ia-1),
i+(ja-1)}
u is a real vector with u_1:i = 0 and u_i+1 = 1
u_i+2:n is stored on return in submatrix A_{i+(ia-1),
i+2+(ja-1):n+(ja-1)}
I is the identity matrix

The following example shows the contents of A on return with ia = ja = 1, m = 6, and n = 5:

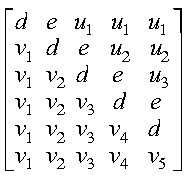
where:

d represents the diagonal elements of B
e represents the off-diagonal elements of B
v_i represents the corresponding elements of the vector defining H_i.
u_i represents the corresponding elements of the vector defining G_i.
If m < n, then B is lower bidiagonal, and matrices Q and P are represented as the product of elementary reflectors:

Q = H₁ H₂ ... H_m-1
P = G₁ G₂ ... G_m

where:

For each i: H_i = I-tau_qvv^T
For each i: G_i = I-tau_puu^T
tau_q and tau_p are real scalars
tau_q is stored on return in:

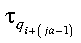
tau_p is stored on return in:

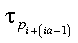
v is a real vector with v_1:i = 0 and v_i+1 = 1
v_i+2:m is stored on return in submatrix A_{i+2+(ia-1):m+(ia-1),
i+(ja-1)}
u is a real vector with u_1:i-1 = 0 and u_i = 1
u_i+1:n is stored on return in submatrix A_{i+(ia-1),
i+1+(ja-1):n+(ja-1)}
I is the identity matrix

The following example shows the contents of A on return with ia = ja = 1, m = 5, and n = 6:

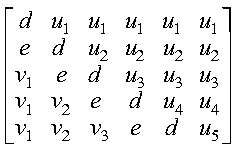
where:

d represents the diagonal elements of B
e represents the off-diagonal elements of B
v_i represents the corresponding elements of the vector defining H_i.
u_i represents the corresponding elements of the vector defining G_i.

Error Conditions

Computational Errors

None

Resource Errors

lwork = 0 and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1

DTYPE_A is invalid.

Stage 2

CTXT_A is invalid.

Stage 3

PDGEBRD has been called from outside the process grid.

Stage 4

m < 0
n < 0
M_A < 0 if m = 0 or n = 0; M_A < 1 otherwise
N_A < 0 if m = 0 or n = 0; N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1

Stage 5

If m <> 0 and n <> 0:

ia > M_A
ja > N_A
ia+m-1 > M_A
ja+n-1 > N_A

In all cases:

MB_A <> NB_A

Stage 6

mod(ia-1, MB_A) <> mod(ja-1, NB_A)
LLD_A < max(1, LOCp(M_A))
lwork <> 0, lwork <> -1, and lwork < nb(mp0+nq0+1)+nq0
where:

nb = MB_A = NB_A
iroffa = mod(ia-1, nb)
icoffa = mod(ja-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow).
iacol = mod(CSRC_A+(ja-1)/nb, npcol).
mp0 = NUMROC(m+iroffa, nb, myrow, iarow, nprow)
nq0 = NUMROC(n+icoffa, nb, mycol, iacol, npcol)

Stage 7

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

m differs.
n differs.
ia differs.
ja differs.
M_A differs.
N_A differs.
DTYPE_A differs.
MB_A differs.
NB_A differs.
RSRC_A differs.
CSRC_A differs.

Also:
lwork = -1 on a subset of processes.

Example

This example shows the reduction of a general matrix of order 4 by 3 to bidiagonal form using a 2 × 2 process grid.
Note: Because lwork = 0, PDGEBRD dynamically allocates the work area used by this subroutine.

Call Statements and Input

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              M   N   A  IA  JA   DESC_A   D   E   TAUQ   TAUP   WORK  LWORK INFO
              |   |   |   |   |     |      |   |    |      |       |     |    |
CALL PDGEBRD( 4 , 3 , A , 1 , 1 , DESC_A , D , E , TAUQ , TAUP , WORK ,  0 , INFO )

DESC_A

DTYPE_

CTXT_

icontxt¹

MB_

NB_

RSRC_

CSRC_

LLD_

See below²

¹ icontxt is the output of the BLACS_GRIDINIT call.

² Each process should set the LLD_ as follows:

LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))

In this example, LLD_A = 2 on all processes.

Global general matrix A of order 4 × 3 with block sizes 2 × 2:

B,D        0          1
     *                    *
 0   | 10.0  5.0  |   9.0 |
     |  2.0 16.0  |  10.0 |
     | -----------|------ |
 1   |  3.0  7.0  |  21.0 |
     |  4.0  8.0  |  12.0 |
     *                    *

The following is the 2 × 2 process grid:

B,D 0 1
0 P₀₀ P₀₁
1 P₁₀ P₁₁

B,D	0	1
0	P₀₀	P₀₁
1	P₁₀	P₁₁

Local arrays for A:

p,q  |     0      |   1
-----|------------|-------
 0   | 10.0  5.0  |   9.0
     |  2.0 16.0  |  10.0
-----|------------|-------
 1   |  3.0  7.0  |  21.0
     |  4.0  8.0  |  12.0

Output:

Global general matrix A of order 4 × 3 with block sizes 2 × 2:

B,D          0             1
     *                          *
 0   | -11.36  22.80  |    0.56 |
     |   0.09  23.32  |    1.67 |
     | ---------------|-------- |
 1   |   0.14   0.46  |   -9.68 |
     |   0.19   0.22  |    0.08 |
     *                          *

The following is the 2 × 2 process grid:

B,D 0 1
0 P₀₀ P₀₁
1 P₁₀ P₁₁

B,D	0	1
0	P₀₀	P₀₁
1	P₁₀	P₁₁

Local arrays for A:

p,q  |       0        |    1
-----|----------------|---------
 0   | -11.36  22.80  |    0.56
     |   0.09  23.32  |    1.67
-----|----------------|---------
 1   |   0.14   0.46  |   -9.68
     |   0.19   0.22  |    0.08

Global row vector D of length 3 with block size 2:

B,D          0             1
     *                          *
 0   | -11.36  23.32  |   -9.68 |
     *                          *

Note:

A copy of D is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 1

P₀₀ P₀₁

P₁₀ P₁₁

B,D	0	1
	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for D:

p,q  |       0        |    1
-----|----------------|---------
 0   | -11.36  23.32  |   -9.68
-----|----------------|---------
 1   | -11.36  23.32  |   -9.68

Global column vector E of length 2 with block size 2:

B,D      0
     *       *
 0   | 22.80 |
     |  1.67 |
     *       *

Note:

A copy of E is distributed across each column of the process grid.

The following is the 2 × 2 process grid:

B,D

0 P₀₀ P₀₁

P₁₀ P₁₁

B,D
0	P₀₀	P₀₁
	P₁₀	P₁₁

Local arrays for E:

p,q  |   0    |    1
-----|--------|--------
 0   | 22.80  |  22.80
     |  1.67  |   1.67
-----|--------|--------
 1   |  .     |   .

Global row vector tau_q of length 3 with block size 2:

B,D         0            1
     *                       *
 0   |  1.88  1.59  |   1.99 |
     *                       *

Note:

A copy of tau_q is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D 0 1

P₀₀ P₀₁

P₁₀ P₁₁

Local arrays for tau_q:

p,q  |      0       |    1
-----|--------------|--------
 0   |  1.88  1.59  |   1.99
-----|--------------|--------
 1   |  1.88  1.59  |   1.99

Global column vector tau_p of length 3 with block size 2:

B,D      0
     *       *
 0   |  1.52 |
     |  0.00 |
     | ----- |
 1   |  0.00 |
     *       *

Note:

A copy of tau_p is distributed across each column of the process grid.

The following is the 2 × 2 process grid:

B,D

0 P₀₀ P₀₁
1 P₁₀ P₁₁

Local arrays for tau_p:

p,q  |   0    |    1
-----|--------|--------
 0   |  1.52  |   1.52
     |  0.00  |   0.00
-----|--------|--------
 1   |  0.00  |   0.00

The value of info is 0 on all processes.

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]

A, `vl`, `vu`, `abstol`, `orfac`, Z, w, `work`, *gap*	`iwork`, *ifail, iclustr*	Subroutine
Long-precision real	Integer	PDSYEVX

A, d, e, tau, `work`	Subroutine
Long-precision real	PDSYTRD

A, d, e, tau_q, tau_p, `work`	Subroutine
Long-precision real	PDGEBRD