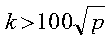Guide and Reference
The Fortran 77 sparse linear algebraic equation subroutines provide
solutions to linear systems of equations for a real general sparse matrix. The
sparse utility subroutines provided in Parallel ESSL must be used in
conjunction with the sparse linear algebraic equation subroutines.
Table 57. List of The Fortran 77 Sparse Linear Algebraic Equation Subroutines
This section contains the dense linear algebraic equation subroutine
descriptions.
These subroutines factor general matrix A using Gaussian
elimination with partial pivoting, ipvt, to compute the
LU factorization of A, where, in this description:
- A represents the global general submatrix
Aia:ia+m-1,
ja:ja+n-1 to be factored.
- ipvt represents the global vector
ipvtia:ia+m-1
containing the pivoting information.
- L is a lower triangular matrix.
- U is an upper triangular matrix.
On output, the transformed matrix A contains U in the
upper triangle (if m >= n) or upper trapezoid (if
m < n). In its strict lower triangle (if
m <= n) or lower trapezoid (if
m > n), it contains the multipliers necessary to
construct, with the help of ipvt, a matrix L, such that
A = LU.
To solve the system of equations with any number of right-hand sides,
follow the call to these subroutines with one or more calls to PDGETRS or
PZGETRS, respectively.
If m = 0 or n = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
references [16], [18], [22], [36],
and [37].
Table 58. Data Types
| A
| ipvt
| Subroutine
|
| Long-precision real
| Integer
| PDGETRF
|
| Long-precision complex
| Integer
| PZGETRF
|
| Fortran
| CALL PDGETRF | PZGETRF (m, n, a, ia,
ja, desc_a, ipvt, info)
|
| C and C++
| pdgetrf | pzgetrf (m, n, a, ia,
ja, desc_a, ipvt, info);
|
- m
- is the number of rows in submatrix A and the number of elements
in vector ipvt used in the computation.
Scope: global
Specified as: a fullword integer; m >= 0.
- n
- is the number of columns in submatrix A used in the
computation.
Scope: global
Specified as: a fullword integer; n >= 0.
- a
- is the local part of the global general matrix A, used in the
system of equations. This identifies the first element of the local
array A. This subroutine computes the location of the first element
of the local subarray used, based on ia, ja,
desc_a, p, q, myrow, and mycol;
therefore, the leading LOCp(ia+m-1) by
LOCq(ja+n-1) part of the local array A must
contain the local pieces of the leading ia+m-1 by
ja+n-1 part of the global matrix.
Scope: local
Specified as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 58. Details about the square block-cyclic data distribution of global matrix
A are stored in desc_a.
- ia
- is the row index of the global matrix A, identifying the first
row of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ia <= M_A and
ia+m-1 <= M_A.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, described in the
following table:
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A=1
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If m = 0 or n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If m = 0 or n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_A < q
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= max(1,LOCp(M_A))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- ipvt
- See 'On Return'.
- info
- See 'On Return'.
- a
- is the updated local part of the global matrix A, containing
the results of the factorization.
Scope: local
Returned as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 58.
- ipvt
- is the local part of the global vector ipvt, containing the
pivot information necessary to construct matrix L from the
information contained in the (output) transformed matrix A. This
identifies the first element of the local array IPVT.
This subroutine computes the location of the first element of the local
subarray used, based on ia, desc_a, p, and
myrow; therefore, the leading LOCp(ia+m-1)
part of the local array IPVT must contain the local pieces of the
leading ia+m-1 part of the global vector.
A copy of the vector ipvt, with a block size of MB_A and global
index ia, is returned to each column of the process grid. The process
row over which the first row of ipvt is distributed is RSRC_A.
Scope: local
Returned as: an array of (at least) length
LOCp(ia+m-1), containing fullword integers, where
ia <= (pivoting
indices) <= ia+m-1. Details about the
block-cyclic data distribution of global vector ipvt are stored in
desc_a.
- info
- has the following meaning:
If info = 0, global submatrix A is not
singular, and the factorization completed normally.
If info > 0, global submatrix A is singular;
that is, one or more columns of L and the corresponding diagonal of
U contain all zeros. All columns of L are checked.
info is set equal to i, the first column of L
with a corresponding U = 0 diagonal element, encountered at
Aia+i-1,
ja+i-1. The factorization is completed; however,
if you call PDGETRS/PZGETRS with these factors, results are
unpredictable.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- The matrix and vector must have no common elements; otherwise, results are
unpredictable.
- The scalar data specified for input argument n must be the same
for both PDGETRF/PZGETRF and PDGETRS/PZGETRS. In addition,
the scalar data specified for input argument m in
PDGETRF/PZGETRF must be the same as input argument
n in both PDGETRF/PZGETRF and PDGETRS/PZGETRS.
If, however, you do not plan to call PDGETRS/PZGETRS
after calling PDGETRF/PZGETRF, then input arguments m and
n in PDGETRF/PZGETRF do not need to be equal.
- The global submatrices for A and ipvt input to
PDGETRS/PZGETRS must be the same as for the corresponding output
arguments for PDGETRF/PZGETRF; and thus, the scalar data specified
for ia, ja, and the contents of desc_a must also be
the same.
- The NUMROC utility subroutine can be used to determine the values of
LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details,
see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
- The way these subroutines handle singularity differs from ScaLAPACK. These
subroutines use the info argument to provide information about the
singularity of A, like ScaLAPACK, but also provide an error
message.
- On both input and output, matrix A conforms to ScaLAPACK
format.
- The global general matrix A must be distributed using a square
block-cyclic distribution; that is, MB_A = NB_A.
- The global general matrix A must be aligned on a block row
boundary; that is, ia-1 must be a multiple of MB_A.
- The block row offset of A must be equal to the block column
offset of A; that is, mod(ia-1,
MB_A) = mod(ja-1, NB_A).
- There is no array descriptor for ipvt. It is a
column-distributed vector with block size MB_A, local arrays of dimension
LOCp(ia+m-1) by 1, and global index ia. A
copy of this vector exists on each column of the process grid, and the process
row over which the first column of ipvt is distributed is RSRC_A.
- For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
- Pivoting imposes additional communication requirements over the process
grid columns; therefore, you achieve optimal performance by using a process
grid with p < q. On the other hand, a
p × 1 grid provides the worse possible configuration.
- For optimal performance, take the following items into consideration when
choosing the NB_A (= MB_A) value:
- The cache size of the computational nodes. NB_A determines the granularity
of the most expensive part of the computation, which tends to increase the
optimal value of NB_A.
- The communication and synchronization overhead. This has two aspects, the
cost of internal synchronization points and the cost of broadcasts. These tend
to slightly decrease the optimal value of NB_A.
- The model of communication adapter you are using. The High Performance
Switch Adapter-2 allows a larger NB.
- Load balancing. For the best processor utilization, it is necessary for
the processor nodes to be active for as long as possible; therefore, each one
should have as many blocks as possible. For a given problem size, this tends
to decrease the optimal value of NB_A (best load balancing: 1) and is
most relevant at very small problem sizes.
- If NB_A is equal to a power of 2, performance may be degraded.
- Use the following rules of thumb for reasonably-sized problems:
- For the POWER processors, choose NB_A in the following range:
- For PDGETRF, use [30, 50], avoiding 32.
- For PZGETRF, use [10, 25], avoiding 16.
- For the POWER2 processors, choose NB_A in the following range:
- For PDGETRF, use [60, 80], avoiding 64.
- For PZGETRF, use [20, 40], avoiding 32.
Matrix A is a singular matrix. For details,
see the description of the info argument.
Unable to allocate work space
- DTYPE_A is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
- m < 0
- n < 0
- M_A < 0 and (m = 0 or n = 0);
M_A < 1 otherwise
- N_A < 0 and (m = 0 or n = 0);
N_A < 1 otherwise
- ia < 1
- ja < 1
- MB_A < 1
- NB_A < 1
- RSRC_A < 0 or RSRC_A >= p
- CSRC_A < 0 or CSRC_A >= q
If m <> 0 and n <> 0:
- ia > M_A
- ja > N_A
- ia+m-1 > M_A
- ja+n-1 > N_A
In all cases:
- MB_A <> NB_A
- mod(ia-1, MB_A) <> mod(ja-1, NB_A)
- mod(ia-1, MB_A) <> 0
- LLD_A < max(1, LOCp(M_A))
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- m differs.
- n differs.
- ia differs.
- ja differs.
- DTYPE_A differs.
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
This example factors a 9 × 9
real general matrix using a 2 × 2 process grid. By specifying
RSRC_A = 1, the rows of global matrix A and the elements of
global vector ipvt are distributed over the process grid starting
in the second row of the process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
M N A IA JA DESC_A IPVT INFO
| | | | | | | |
CALL PDGETRF( 9 , 9 , A , 1 , 1 , DESC_A , IPVT , INFO )
| Desc_A
|
| DTYPE_
| 1
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| N_
| 9
|
| MB_
| 3
|
| NB_
| 3
|
| RSRC_
| 1
|
| CSRC_
| 0
|
| LLD_
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
In this example, LLD_A = 3 on P00 and P01,
and LLD_A = 6 on P10 and P11.
|
|
Global general 9 × 9 matrix A with block size
3 × 3:
B,D 0 1 2
* *
| 1.0 1.2 1.4 | 1.6 1.8 2.0 | 2.2 2.4 2.6 |
0 | 1.2 1.0 1.2 | 1.4 1.6 1.8 | 2.0 2.2 2.4 |
| 1.4 1.2 1.0 | 1.2 1.4 1.6 | 1.8 2.0 2.2 |
| ----------------|------------------|---------------- |
| 1.6 1.4 1.2 | 1.0 1.2 1.4 | 1.6 1.8 2.0 |
1 | 1.8 1.6 1.4 | 1.2 1.0 1.2 | 1.4 1.6 1.8 |
| 2.0 1.8 1.6 | 1.4 1.2 1.0 | 1.2 1.4 1.6 |
| ----------------|------------------|---------------- |
| 2.2 2.0 1.8 | 1.6 1.4 1.2 | 1.0 1.2 1.4 |
2 | 2.4 2.2 2.0 | 1.8 1.6 1.4 | 1.2 1.0 1.2 |
| 2.6 2.4 2.2 | 2.0 1.8 1.6 | 1.4 1.2 1.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of A begins in the second row of the process grid.
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------|-----------------
| 1.6 1.4 1.2 1.6 1.8 2.0 | 1.0 1.2 1.4
0 | 1.8 1.6 1.4 1.4 1.6 1.8 | 1.2 1.0 1.2
| 2.0 1.8 1.6 1.2 1.4 1.6 | 1.5 1.3 1.0
-----|--------------------------------|-----------------
| 1.0 1.2 1.4 2.2 2.4 2.6 | 1.6 1.8 2.0
| 1.2 1.0 1.2 2.0 2.2 2.4 | 1.4 1.6 1.8
| 1.4 1.2 1.0 1.8 2.0 2.2 | 1.2 1.4 1.6
1 | 2.2 2.0 1.8 1.0 1.2 1.4 | 1.6 1.4 1.2
| 2.4 2.2 2.0 1.2 1.0 1.2 | 1.8 1.6 1.4
| 2.6 2.4 2.2 1.4 1.2 1.0 | 2.0 1.8 1.6
Output:
Global general 9 × 9 transformed matrix A with
block size 3 × 3:
B,D 0 1 2
* *
| 2.6 2.4 2.2 | 2.0 1.8 1.6 | 1.4 1.2 1.0 |
0 | 0.4 0.3 0.6 | 0.8 1.1 1.4 | 1.7 1.9 2.2 |
| 0.5 -0.4 0.4 | 0.8 1.2 1.6 | 2.0 2.4 2.8 |
| ----------------|------------------|---------------- |
| 0.5 -0.3 0.0 | 0.4 0.8 1.2 | 1.6 2.0 2.4 |
1 | 0.6 -0.3 0.0 | 0.0 0.4 0.8 | 1.2 1.6 2.0 |
| 0.7 -0.2 0.0 | 0.0 0.0 0.4 | 0.8 1.2 1.6 |
| ----------------|------------------|---------------- |
| 0.8 -0.2 0.0 | 0.0 0.0 0.0 | 0.4 0.8 1.2 |
2 | 0.8 -0.1 0.0 | 0.0 0.0 0.0 | 0.0 0.4 0.8 |
| 0.9 -0.1 0.0 | 0.0 0.0 0.0 | 0.0 0.0 0.4 |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of A begins in the second row of the process grid.
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------|-----------------
| 0.5 -0.3 0.0 1.6 2.0 2.4 | 0.4 0.8 1.2
0 | 0.6 -0.3 0.0 1.2 1.6 2.0 | 0.0 0.4 0.8
| 0.7 -0.2 0.0 0.8 1.2 1.6 | 0.0 0.0 0.4
-----|--------------------------------|-----------------
| 2.6 2.4 2.2 1.4 1.2 1.0 | 2.0 1.8 1.6
| 0.4 0.3 0.6 1.7 1.9 2.2 | 0.8 1.1 1.4
| 0.5 -0.4 0.4 2.0 2.4 2.8 | 0.8 1.2 1.6
1 | 0.8 -0.2 0.0 0.4 0.8 1.2 | 0.0 0.0 0.0
| 0.8 -0.1 0.0 0.0 0.4 0.8 | 0.0 0.0 0.0
| 0.9 -0.1 0.0 0.0 0.0 0.4 | 0.0 0.0 0.0
Global vector ipvt of length 9 with block size 3:
B,D 0
* *
| 9 |
0 | 9 |
| 9 |
| -- |
| 9 |
1 | 9 |
| 9 |
| -- |
| 9 |
2 | 9 |
| 9 |
* *
| Note: |
A copy of ipvt is distributed across each column of the process
grid.
|
The following is the 2 × 2 process grid:
| B,D
|
|
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of ipvt begins in the second row of the process grid.
|
Local arrays for ipvt:
p,q | 0 | 1
-----|-----|-----
| 9 | 9
0 | 9 | 9
| 9 | 9
-----|-----|-----
| 9 | 9
| 9 | 9
| 9 | 9
1 | 9 | 9
| 9 | 9
| 9 | 9
The value of info is 0 on all processes.
This example factors a 9 × 9
complex matrix using a 2 × 2 process grid. By specifying
RSRC_A = 1, the rows of global matrix A and the elements of
global vector ipvt are distributed over the process grid starting
in the second row of the process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
M N A IA JA DESC_A IPVT INFO
| | | | | | | |
CALL PZGETRF( 9 , 9 , A , 1 , 1 , DESC_A , IPVT , INFO )
| Desc_A
|
| DTYPE_
| 1
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| N_
| 9
|
| MB_
| 3
|
| NB_
| 3
|
| RSRC_
| 1
|
| CSRC_
| 0
|
| LLD_
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
In this example, LLD_A = 3 on P00 and P01,
and LLD_A = 6 on P10 and P11.
|
|
Global general 9 × 9 matrix A with block size
3 × 3:
B,D 0 1 2
* *
| (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) | (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) | (4.4,-1.0) (4.8,-1.0) (5.2,-1.0) |
0 | (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) | (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) | (4.0,-1.0) (4.4,-1.0) (4.8,-1.0) |
| (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) | (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) | (3.6,-1.0) (4.0,-1.0) (4.4,-1.0) |
| -------------------------------------|---------------------------------------|------------------------------------- |
| (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) | (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) | (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) |
1 | (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) | (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) | (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) |
| (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) | (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) | (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) |
| -------------------------------------|---------------------------------------|------------------------------------- |
| (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) | (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) | (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) |
2 | (4.8, 1.0) (4.4, 1.0) (4.0, 1.0) | (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) | (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) |
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) | (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) | (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of A begins in the second row of the process grid.
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------------------------------------------------|--------------------------------------
| (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) | (2.0, 1.0) (2.4,-1.0) (2.8,-1.0)
0 | (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) | (2.4, 1.0) (2.0, 1.0) (2.4,-1.0)
| (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) | (2.8, 1.0) (2.4, 1.0) (2.0, 1.0)
-----|--------------------------------------------------------------------------|--------------------------------------
| (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (4.4,-1.0) (4.8,-1.0) (5.2,-1.0) | (3.2,-1.0) (3.6,-1.0) (4.0,-1.0)
| (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (4.0,-1.0) (4.4,-1.0) (4.8,-1.0) | (2.8,-1.0) (3.2,-1.0) (3.6,-1.0)
| (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (3.6,-1.0) (4.0,-1.0) (4.4,-1.0) | (2.4,-1.0) (2.8,-1.0) (3.2,-1.0)
1 | (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) | (3.2, 1.0) (2.8, 1.0) (2.4, 1.0)
| (4.8, 1.0) (4.4, 1.0) (4.0, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) | (3.6, 1.0) (3.2, 1.0) (2.8, 1.0)
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) | (4.0, 1.0) (3.6, 1.0) (3.2, 1.0)
Output:
Global general 9 × 9 transformed matrix A with
block size 3 × 3:
B,D 0 1 2
* *
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) | (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) | (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) |
0 | (0.4, 0.1) (0.6,-2.0) (1.1,-1.9) | (1.7,-1.9) (2.3,-1.8) (2.8,-1.8) | (3.4,-1.7) (3.9,-1.7) (4.5,-1.6) |
| (0.5, 0.1) (0.0,-0.1) (0.6,-1.9) | (1.2,-1.8) (1.8,-1.7) (2.5,-1.6) | (3.1,-1.5) (3.7,-1.4) (4.3,-1.3) |
| --------------------------------------|-----------------------------------------|------------------------------------- |
| (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) | (0.7,-1.9) (1.3,-1.7) (2.0,-1.6) | (2.7,-1.5) (3.4,-1.4) (4.0,-1.2) |
1 | (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) | (-0.1, 0.0) (0.7,-1.9) (1.5,-1.7) | (2.2,-1.6) (2.9,-1.5) (3.7,-1.3) |
| (0.7, 0.1) (0.0,-0.1) (0.0, 0.0) | (-0.1, 0.0) (-0.1, 0.0) (0.8,-1.9) | (1.6,-1.8) (2.4,-1.6) (3.2,-1.5) |
| --------------------------------------|-----------------------------------------|------------------------------------- |
| (0.8, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.8,-1.9) (1.7,-1.8) (2.5,-1.8) |
2 | (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.0, 0.0) (0.8,-2.0) (1.7,-1.9) |
| (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) | (0.0, 0.0) (0.0, 0.0) (0.8,-2.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of A begins in the second row of the process grid.
|
Local arrays for A:
p,q | 0 | 1
-----|---------------------------------------------------------------------------|----------------------------------------
| (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) (2.7,-1.5) (3.4,-1.4) (4.0,-1.2) | (0.7,-1.9) (1.3,-1.7) (2.0,-1.6)
0 | (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) (2.2,-1.6) (2.9,-1.5) (3.7,-1.3) | (-0.1, 0.0) (0.7,-1.9) (1.5,-1.7)
| (0.7, 0.1) (0.0,-0.1) (0.0, 0.0) (1.6,-1.8) (2.4,-1.6) (3.2,-1.5) | (-0.1, 0.0) (-0.1, 0.0) (0.8,-1.9)
-----|---------------------------------------------------------------------------|----------------------------------------
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) | (4.0, 1.0) (3.6, 1.0) (3.2, 1.0)
| (0.4, 0.1) (0.6,-2.0) (1.1,-1.9) (3.4,-1.7) (3.9,-1.7) (4.5,-1.6) | (1.7,-1.9) (2.3,-1.8) (2.8,-1.8)
| (0.5, 0.1) (0.0,-0.1) (0.6,-1.9) (3.1,-1.5) (3.7,-1.4) (4.3,-1.3) | (1.2,-1.8) (1.8,-1.7) (2.5,-1.6)
1 | (0.8, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-1.9) (1.7,-1.8) (2.5,-1.8) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0)
| (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-2.0) (1.7,-1.9) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0)
| (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-2.0) | (0.0, 0.0) (0.0, 0.0) (0.0, 0.0)
Global vector ipvt of length 9 with block size 3:
B,D 0
* *
| 9 |
0 | 9 |
| 9 |
| -- |
| 9 |
1 | 9 |
| 9 |
| -- |
| 9 |
2 | 9 |
| 9 |
* *
| Note: |
A copy of ipvt is distributed across each column of the process
grid.
|
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of ipvt begins in the second row of the process grid.
|
Local arrays for ipvt:
p,q | 0 | 1
-----|-----|-----
| 9 | 9
0 | 9 | 9
| 9 | 9
-----|-----|-----
| 9 | 9
| 9 | 9
| 9 | 9
1 | 9 | 9
| 9 | 9
| 9 | 9
The value of info is 0 on all processes.
PDGETRS solves one of the following systems of equations for multiple
right-hand sides:
- 1. AX = B
- 2. ATX = B
PZGETRS solves one of the following systems of equations for multiple
right-hand sides:
- 1. AX = B
- 2. ATX = B
- 3. AHX = B
In the formulas above:
- A represents the global general submatrix
Aia:ia+n-1,
ja:ja+n-1 containing the
LU factorization.
- B represents the global general submatrix
Bib:ib+n-1,
jb:jb+nrhs-1 containing the
right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
jb:jb+nrhs-1 containing the
solution vectors in its columns.
This subroutine uses the results of the factorization of matrix
A, produced by a preceding call to PDGETRF or PZGETRF,
respectively. On input, the transformed matrix A consists of the
upper triangular matrix U and the multipliers necessary to
construct L using ipvt, which represents the global
vector
ipvtia:ia+n-1.
For details on the factorization, see PDGETRF and PZGETRF--General Matrix Factorization.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
references [16], [18], [22], [36],
and [37].
Table 59. Data Types
| A, B
| ipvt
| Subroutine
|
| Long-precision real
| Integer
| PDGETRS
|
| Long-precision complex
| Integer
| PZGETRS
|
| Fortran
| CALL PDGETRS | PZGETRS (transa, n, nrhs,
a, ia, ja, desc_a, ipvt,
b, ib, jb, desc_b, info)
|
| C and C++
| pdgetrs | pzgetrs (transa, n, nrhs,
a, ia, ja, desc_a, ipvt,
b, ib, jb, desc_b, info);
|
- transa
- indicates the form of matrix A to use in the computation,
where:
If transa = 'N', A is used in the
computation, resulting in solution 1.
If transa = 'T', AT is used
in the computation, resulting in solution 2.
If transa = 'C', AH is used
in the computation, resulting in solution 3.
Scope: global
Specified as: a single character;
transa = 'N', 'T', or 'C'.
- n
- is the order of the factored matrix A and the number of rows in
submatrix B.
Scope: global
Specified as: a fullword integer; n >= 0.
- nrhs
- is the number of right-hand sides-- that is, the number of columns
in submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- a
- is the local part of the global general matrix A, containing
the factorization of matrix A produced by a preceding call to
PDGETRF or PZGETRF, respectively. This identifies the first element
of the local array A. This subroutine computes the location of the
first element of the local subarray used, based on ia, ja,
desc_a, p, q, myrow, and mycol;
therefore, the leading LOCp(ia+n-1) by
LOCq(ja+n-1) part of the local array A must
contain the local pieces of the leading ia+n-1 by
ja+n-1 part of the global matrix.
Scope: local
Specified as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 59. Details about the square block-cyclic data distribution of global matrix
A are stored in desc_a.
- ia
- is the row index of the global matrix A, identifying the first
row of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ia <= M_A and
ia+n-1 <= M_A.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, described in the
following table:
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A=1
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_A < q
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= max(1,LOCp(M_A))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- ipvt
- is the local part of the global vector ipvt, containing the
pivoting indices produced on a preceding call to PDGETRF or PZGETRF,
respectively. This identifies the first element of the local array
IPVT. This subroutine computes the location of the first element of
the local subarray used, based on ia, desc_a, p,
and myrow; therefore, the leading
LOCp(ia+n-1) part of the local array IPVT
must contain the local pieces of the leading ia+n-1
part of the global vector.
A copy of the vector ipvt, with a block size of MB_A and global
index ia, is contained in each column of the process grid. The
process row over which the first row of ipvt is distributed is
RSRC_A.
Scope: local
Specified as: an array of (at least) length
LOCp(ia+n-1), containing fullword integers, where
ia <= (pivoting index
values) <= ia+m-1, and m is an
argument in PDGETRF and PZGETRF. Details about the block-cyclic data
distribution of global vector ipvt are stored in desc_a.
- b
- is the local part of the global general matrix B, containing
the right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, jb, desc_b, p, q,
myrow, and mycol; therefore, the leading
LOCp(ib+n-1) by
LOCq(jb+nrhs-1) part of the local array B
must contain the local pieces of the leading ib+n-1 by
jb+nrhs-1 part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) LOCq(N_B) array, containing
numbers of the data type indicated in Table 59. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- jb
- is the column index of the global matrix B, identifying the
first column of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= jb <= N_B and
jb+nrhs-1 <= N_B.
- desc_b
- is the array descriptor for global matrix B, described in the
following table:
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B=1
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0 or nrhs = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
|
If n = 0 or nrhs = 0:
N_B >= 0
Otherwise:
N_B >= 1
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_B < q
| Global
|
| 9
| LLD_B
| The leading dimension of the local array
| LLD_B >= max(1,LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- info
- See 'On Return'.
- b
- is the updated local part of the global matrix B, containing
the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) LOCq(N_B) array, containing
numbers of the data type indicated in Table 59.
- info
- indicates that a successful computation occurred.
Scope: global
Returned as: a fullword integer; info = 0.
- In your C program, argument info must be passed by reference.
- This subroutine accepts lowercase letters for the transa
argument.
- For PDGETRS, if you specify 'C' for the transa argument,
it is interpreted as though you specified 'T'.
- The matrices and vector must have no common elements; otherwise, results
are unpredictable.
- The scalar data specified for input argument n must be the same
for both PDGETRF/PZGETRF and PDGETRS/PZGETRS. In addition,
the scalar data specified for input argument m in
PDGETRF/PZGETRF must be the same as input argument
n in both PDGETRF/PZGETRF and PDGETRS/PZGETRS.
If, however, you do not plan to call PDGETRS/PZGETRS
after calling PDGETRF/PZGETRF, then input arguments m and
n in PDGETRF/PZGETRF do not need to be equal.
- The global submatrices for A and ipvt input to
PDGETRS/PZGETRS must be the same as for the corresponding output
arguments for PDGETRF/PZGETRF; and thus, the scalar data specified
for ia, ja, and the contents of desc_a must also be
the same.
- The NUMROC utility subroutine can be used to determine the values of
LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details,
see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
- For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
- On both input and output, matrices A and B conform
to ScaLAPACK format.
- The following values must be equal: CTXT_A = CTXT_B.
- The global general matrix A must be distributed using a square
block-cyclic distribution; that is, MB_A = NB_A.
- The following block sizes must be equal: MB_A = MB_B.
- The global general matrix A must be aligned on a block row
boundary; that is, ia-1 must be a multiple of MB_A.
- The block row offset of A must be equal to the block column
offset of A; that is, mod(ia-1,
MB_A) = mod(ja-1, NB_A).
- The block row offset of A must be equal to the block row offset
of B; that is, mod(ia-1,
MB_A) = mod(ib-1, MB_B).
- In the process grid, the process row containing the first row of the
submatrix A must also contain the first row of the submatrix
B; that is, iarow = ibrow, where:
- iarow = mod((((ia-1)/MB_A)+RSRC_A),
p)
- ibrow = mod((((ib-1)/MB_B)+RSRC_B),
p)
- There is no array descriptor for ipvt. It is a
column-distributed vector with block size MB_A, local arrays of dimension
LOCp(ia+m-1) by 1, and global index ia. A
copy of this vector exists on each column of the process grid, and the process
row over which the first column of ipvt is distributed is RSRC_A.
None
| Note: |
If the factorization performed by PDGETRF/PZGETRF failed because of a
singular matrix A, the results returned by this subroutine are
unpredictable. For details, see the info output argument for
PDGETRF/PZGETRF.
|
Unable to allocate work space
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
- transa <> 'N', 'T', or 'C'
- n < 0
- nrhs < 0
- M_A < 0 and n = 0; M_A < 1
otherwise
- N_A < 0 and n = 0; N_A < 1
otherwise
- ia < 1
- ja < 1
- MB_A < 1
- NB_A < 1
- RSRC_A < 0 or RSRC_A >= p
- CSRC_A < 0 or CSRC_A >= q
- M_B < 0 and (n = 0 or
nrhs = 0); M_B < 1 otherwise
- N_B < 0 and (n = 0 or
nrhs = 0); N_B < 1 otherwise
- ib < 1
- jb < 1
- MB_B < 1
- NB_B < 1
- RSRC_B < 0 or RSRC_B >= p
- CSRC_B < 0 or CSRC_B >= q
- CTXT_A <> CTXT_B
If n <> 0:
- ia > M_A
- ja > N_A
- ia+n-1 > M_A
- ja+n-1 > N_A
If n <> 0 and nrhs <> 0:
- ib > M_B
- jb > N_B
- ib+n-1 > M_B
- jb+nrhs-1 > N_B
In all cases:
- MB_A <> NB_A
- mod(ia-1, MB_A) <> mod(ja-1, NB_A)
- MB_B <> MB_A
- mod(ia-1, MB_A) <> mod(ib-1,
MB_B).
- mod(ia-1, MB_A) <> 0
- In the process grid, the process row containing the first row of the
submatrix A does not contain the first row of the submatrix
B; that is, iarow <> ibrow,
where:
- iarow = mod((((ia-1)/MB_A)+RSRC_A),
p)
- ibrow = mod((((ib-1)/MB_B)+RSRC_B),
p)
- LLD_A < max(1, LOCp(M_A))
- LLD_B < max(1, LOCp(M_B))
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- transa differs.
- n differs.
- nrhs differs.
- ipvt differs.
- ia differs.
- ja differs.
- DTYPE_A differs.
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
- ib differs.
- jb differs.
- DTYPE_B differs.
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
This example solves the real system
AX = B with 5 right-hand sides using a
2 × 2 process grid. The input ipvt vector and
transformed matrix A are the output from "Example 1".
This example uses a global submatrix B within a global matrix
B by specifying ib = 1 and
jb = 2.
By specifying RSRC_B = 1, the rows of global matrix B
are distributed over the process grid starting in the second row of the
process grid. In addition, by specifying CSRC_B = 1, the columns of
global matrix B are distributed over the process grid starting in
the second column of the process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
TRANSA N NRHS A IA JA DESC_A IPVT B IB JB DESC_B INFO
| | | | | | | | | | | | |
CALL PDGETRS( 'N' , 9 , 5 , A , 1 , 1 , DESC_A , IPVT , B , 1 , 2 , DESC_B , INFO )
| Desc_A
| Desc_B
|
| DTYPE_
| 1
| 1
|
| CTXT_
| icontxt1
| icontxt1
|
| M_
| 9
| 9
|
| N_
| 9
| 6
|
| MB_
| 3
| 3
|
| NB_
| 3
| 2
|
| RSRC_
| 1
| 1
|
| CSRC_
| 0
| 1
|
| LLD_
| See below2
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW))
In this example, LLD_A = LLD_B = 3 on P00 and
P01, and LLD_A = LLD_B = 6 on P10 and
P11.
|
|
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . 93.0 | 186.0 279.0 | 372.0 465.0 |
0 | . 84.4 | 168.8 253.2 | 337.6 422.0 |
| . 76.6 | 153.2 229.8 | 306.4 383.0 |
| -------------|-----------------|--------------- |
| . 70.0 | 140.0 210.0 | 280.0 350.0 |
1 | . 65.0 | 130.0 195.0 | 260.0 325.0 |
| . 62.0 | 124.0 186.0 | 248.0 310.0 |
| -------------|-----------------|--------------- |
| . 61.4 | 122.8 184.2 | 245.6 307.0 |
2 | . 63.6 | 127.2 190.8 | 254.4 318.0 |
| . 69.0 | 138.0 207.0 | 276.0 345.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of B begins in the second row of the process grid,
and the first column of B begins in the second column of the
process grid.
|
Local arrays for B:
p,q | 0 | 1
-----|----------------|----------------------------
| 140.0 210.0 | . 70.0 280.0 350.0
0 | 130.0 195.0 | . 65.0 260.0 325.0
| 124.0 186.0 | . 62.0 248.0 310.0
-----|----------------|----------------------------
| 186.0 279.0 | . 93.0 372.0 465.0
| 168.8 253.2 | . 84.4 337.6 422.0
| 153.2 229.8 | . 76.6 306.4 383.0
1 | 122.8 184.2 | . 61.4 245.6 307.0
| 127.2 190.8 | . 63.6 254.4 318.0
| 138.0 207.0 | . 69.0 276.0 345.0
Output:
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . 1.0 | 2.0 3.0 | 4.0 5.0 |
0 | . 2.0 | 4.0 6.0 | 8.0 10.0 |
| . 3.0 | 6.0 9.0 | 12.0 15.0 |
| -----------|---------------|------------- |
| . 4.0 | 8.0 12.0 | 16.0 20.0 |
1 | . 5.0 | 10.0 15.0 | 20.0 25.0 |
| . 6.0 | 12.0 18.0 | 24.0 30.0 |
| -----------|---------------|------------- |
| . 7.0 | 14.0 21.0 | 28.0 35.0 |
2 | . 8.0 | 16.0 24.0 | 32.0 40.0 |
| . 9.0 | 18.0 27.0 | 36.0 45.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of B begins in the second row of the process grid,
and the first column of B begins in the second column of the
process grid.
|
Local arrays for B:
p,q | 0 | 1
-----|--------------|------------------------
| 8.0 12.0 | . 4.0 16.0 20.0
0 | 10.0 15.0 | . 5.0 20.0 25.0
| 12.0 18.0 | . 6.0 24.0 30.0
-----|--------------|------------------------
| 2.0 3.0 | . 1.0 4.0 5.0
| 4.0 6.0 | . 2.0 8.0 10.0
| 6.0 9.0 | . 3.0 12.0 15.0
1 | 14.0 21.0 | . 7.0 28.0 35.0
| 16.0 24.0 | . 8.0 32.0 40.0
| 18.0 27.0 | . 9.0 36.0 45.0
The value of info is 0 on all processes.
This example solves the complex system
AX = B with 5 right-hand sides using a
2 × 2 process grid. The input ipvt vector and
transformed matrix A are the output from "Example 2".
This example uses a global submatrix B within a global matrix
B by specifying ib = 1 and
jb = 2.
By specifying RSRC_B = 1, the rows of global matrix B
are distributed over the process grid starting in the second row of the
process grid. In addition, by specifying CSRC_B = 1, the columns of
global matrix B are distributed over the process grid starting in
the second column of the process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
TRANSA N NRHS A IA JA DESC_A IPVT B IB JB DESC_B INFO
| | | | | | | | | | | | |
CALL PZGETRS( 'N' , 9 , 5 , A , 1 , 1 , DESC_A , IPVT , B , 1 , 2 , DESC_B , INFO )
| Desc_A
| Desc_B
|
| DTYPE_
| 1
| 1
|
| CTXT_
| icontxt1
| icontxt1
|
| M_
| 9
| 9
|
| N_
| 9
| 6
|
| MB_
| 3
| 3
|
| NB_
| 3
| 2
|
| RSRC_
| 1
| 1
|
| CSRC_
| 0
| 1
|
| LLD_
| See below2
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW))
In this example, LLD_A = LLD_B = 3 on P00 and
P01, and LLD_A = LLD_B = 6 on P10 and
P11.
|
|
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . (193.0,-10.6) | (200.0, 21.8) (207.0, 54.2) | (214.0, 86.6) (221.0,119.0) |
0 | . (173.8, -9.4) | (178.8, 20.2) (183.8, 49.8) | (188.8, 79.4) (193.8,109.0) |
| . (156.2, -5.4) | (159.2, 22.2) (162.2, 49.8) | (165.2, 77.4) (168.2,105.0) |
| ----------------------|---------------------------------|------------------------------- |
| . (141.0, 1.4) | (142.0, 27.8) (143.0, 54.2) | (144.0, 80.6) (145.0,107.0) |
1 | . (129.0, 11.0) | (128.0, 37.0) (127.0, 63.0) | (126.0, 89.0) (125.0,115.0) |
| . (121.0, 23.4) | (118.0, 49.8) (115.0, 76.2) | (112.0,102.6) (109.0,129.0) |
| ----------------------|---------------------------------|------------------------------- |
| . (117.8, 38.6) | (112.8, 66.2) (107.8, 93.8) | (102.8,121.4) (97.8,149.0) |
2 | . (120.2, 56.6) | (113.2, 86.2) (106.2,115.8) | (99.2,145.4) (92.2,175.0) |
| . (129.0, 77.4) | (120.0,109.8) (111.0,142.2) | (102.0,174.6) (93.0,207.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of B begins in the second row of the process grid,
and the first column of B begins in the second column of the
process grid.
|
Local arrays for B:
p,q | 0 | 1
-----|--------------------------------|-----------------------------------------------------
| (142.0, 27.8) (143.0, 54.2) | . (141.0, 1.4) (144.0, 80.6) (145.0,107.0)
0 | (128.0, 37.0) (127.0, 63.0) | . (129.0, 11.0) (126.0, 89.0) (125.0,115.0)
| (118.0, 49.8) (115.0, 76.2) | . (121.0, 23.4) (112.0,102.6) (109.0,129.0)
-----|--------------------------------|-----------------------------------------------------
| (200.0, 21.8) (207.0, 54.2) | . (193.0,-10.6) (214.0, 86.6) (221.0,119.0)
| (178.8, 20.2) (183.8, 49.8) | . (173.8, -9.4) (188.8, 79.4) (193.8,109.0)
| (159.2, 22.2) (162.2, 49.8) | . (156.2, -5.4) (165.2, 77.4) (168.2,105.0)
1 | (112.8, 66.2) (107.8, 93.8) | . (117.8, 38.6) (102.8,121.4) (97.8,149.0)
| (113.2, 86.2) (106.2,115.8) | . (120.2, 56.6) (99.2,145.4) (92.2,175.0)
| (120.0,109.8) (111.0,142.2) | . (129.0, 77.4) (102.0,174.6) (93.0,207.0)
Output:
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . (1.0, 1.0) | (1.0, 2.0) (1.0, 3.0) | (1.0, 4.0) (1.0, 5.0) |
0 | . (2.0, 1.0) | (2.0, 2.0) (2.0, 3.0) | (2.0, 4.0) (2.0, 5.0) |
| . (3.0, 1.0) | (3.0, 2.0) (3.0, 3.0) | (3.0, 4.0) (3.0, 5.0) |
| ------------------|---------------------------|------------------------- |
| . (4.0, 1.0) | (4.0, 2.0) (4.0, 3.0) | (4.0, 4.0) (4.0, 5.0) |
1 | . (5.0, 1.0) | (5.0, 2.0) (5.0, 3.0) | (5.0, 4.0) (5.0, 5.0) |
| . (6.0, 1.0) | (6.0, 2.0) (6.0, 3.0) | (6.0, 4.0) (6.0, 5.0) |
| ------------------|---------------------------|------------------------- |
| . (7.0, 1.0) | (7.0, 2.0) (7.0, 3.0) | (7.0, 4.0) (7.0, 5.0) |
2 | . (8.0, 1.0) | (8.0, 2.0) (8.0, 3.0) | (8.0, 4.0) (8.0, 5.0) |
| . (9.0, 1.0) | (9.0, 2.0) (9.0, 3.0) | (9.0, 4.0) (9.0, 5.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 1
| P00
| P01
|
| 0
2
| P10
| P11
|
| Note: |
The first row of B begins in the second row of the process grid,
and the first column of B begins in the second column of the
process grid.
|
Local arrays for B:
p,q | 0 | 1
-----|--------------------------|-------------------------------------------
| (3.0, 2.0) (3.0, 3.0) | . (3.0, 1.0) (3.0, 4.0) (3.0, 5.0)
0 | (4.0, 2.0) (4.0, 3.0) | . (4.0, 1.0) (4.0, 4.0) (4.0, 5.0)
| (5.0, 2.0) (5.0, 3.0) | . (5.0, 1.0) (5.0, 4.0) (5.0, 5.0)
-----|--------------------------|-------------------------------------------
| (1.0, 2.0) (1.0, 3.0) | . (1.0, 1.0) (1.0, 4.0) (1.0, 5.0)
| (2.0, 2.0) (2.0, 3.0) | . (2.0, 1.0) (2.0, 4.0) (2.0, 5.0)
| (3.0, 2.0) (3.0, 3.0) | . (3.0, 1.0) (3.0, 4.0) (3.0, 5.0)
1 | (7.0, 2.0) (7.0, 3.0) | . (7.0, 1.0) (7.0, 4.0) (7.0, 5.0)
| (8.0, 2.0) (8.0, 3.0) | . (8.0, 1.0) (8.0, 4.0) (8.0, 5.0)
| (9.0, 2.0) (9.0, 3.0) | . (9.0, 1.0) (9.0, 4.0) (9.0, 5.0)
The value of info is 0 on all processes.
PDPOTRF uses Cholesky factorization to factor a positive definite real
symmetric matrix A into one of the following forms:
- A = LLT if A is lower
triangular.
- A = UTU if
A is upper triangular.
PZPOTRF uses Cholesky factorization to factor a positive definite complex
Hermitian matrix A into one of the following forms:
- A = LLH if A is lower
triangular.
- A = UHU if
A is upper triangular.
In the formulas above:
- A represents the global positive definite real symmetric or
complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 to be factored.
- L is a lower triangular matrix.
- U is an upper triangular matrix.
To solve the system of equations with any number of right-hand sides,
follow the call to these subroutines with one or more calls to PDPOTRS or
PZPOTRS, respectively.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See references [16], [18], [22], [36],
and [37].
Table 60. Data Types
| A
| Subroutine
|
| Long-precision real
| PDPOTRF
|
| Long-precision complex
| PZPOTRF
|
| Fortran
| CALL PDPOTRF | PZPOTRF (uplo, n, a,
ia, ja, desc_a, info)
|
| C and C++
| pdpotrf | pzpotrf (uplo, n, a, ia,
ja, desc_a, info);
|
- uplo
- indicates whether the upper or lower triangular part of the global real
symmetric or complex Hermitian submatrix A is referenced,
where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character; uplo = 'U'
or 'L'.
- n
- is the number of rows and columns in submatrix A used in the
computation.
Scope: global
Specified as: a fullword integer; n >= 0.
- a
- is the local part of the global real symmetric or complex Hermitian matrix
A, used in the system of equations. This identifies the first
element of the local array A. This subroutine computes the
location of the first element of the local subarray used, based on
ia, ja, desc_a, p, q,
myrow, and mycol; therefore, the leading
LOCp(ia+n-1) by LOCq(ja+n-1)
part of the local array A must contain the local pieces of the
leading ia+n-1 by ja+n-1 part
of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global real
symmetric or complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global real
symmetric or complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 60. Details about the square block-cyclic data distribution of global matrix
A are stored in desc_a.
- ia
- is the row index of the global matrix A, identifying the first
row of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ia <= M_A and
ia+n-1 <= M_A.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, described in the
following table:
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A=1
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_A < q
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= max(1,LOCp(M_A))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- info
- See 'On Return'.
- a
- is the updated local part of the global matrix A, containing
the results of the factorization.
Scope: local
Returned as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 60.
- info
- has the following meaning:
If info = 0, global real symmetric or complex Hermitian
submatrix A is positive definite, and the factorization completed
normally.
If info > 0, the leading minor of order k of
the global real symmetric or complex Hermitian submatrix A is not
positive definite. info is set equal to k, where the leading
minor was encountered at Aia+k-1,
ja+k-1. The factorization is not completed.
A is overwritten with the partial factors.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- This subroutine accepts lowercase letters for the uplo argument.
- On input to PZPOTRF, the imaginary parts of the diagonal elements of the
complex Hermitian matrix A are assumed to be zero, so you do not
have to set these values. On output, they are set to zero.
- The scalar data specified for input argument n must be the same
for both PDPOTRF/PZPOTRF and PDPOTRS/PZPOTRS.
- The global submatrix A input to PDPOTRS/PZPOTRS must
be the same as for the corresponding output argument for
PDPOTRF/PZPOTRF; and thus, the scalar data specified for ia,
ja, and the contents of desc_a must also be the same.
- The NUMROC utility subroutine can be used to determine the values of
LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details,
see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
- The way these subroutines handle nonpositive definiteness differs from
ScaLAPACK. These subroutines use the info argument to provide
information about the nonpositive definiteness of A, like
ScaLAPACK, but also provides an error message.
- On both input and output, matrix A conforms to ScaLAPACK
format.
- The global real symmetric or complex Hermitian matrix A must be
distributed using a square block-cyclic distribution; that is,
MB_A = NB_A.
- The global real symmetric or complex Hermitian matrix A must be
aligned on a block row boundary; that is, ia-1 must be a
multiple of MB_A.
- The block row offset of A must be equal to the block column
offset of A; that is, mod(ia-1,
MB_A) = mod(ja-1, NB_A).
- For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
- For optimal performance, you should use a square process grid to minimize
the communication path length in both directions.
- For optimal performance, take the following items into consideration when
choosing the NB_A (= MB_A) value:
- Whether you are using the upper or lower triangular part of A,
which may affect performance.
- The cache size of the computational nodes. NB_A determines the granularity
of the most expensive part of the computation, which tends to increase the
optimal value of NB_A.
- The communication and synchronization overhead. This has two aspects, the
cost of internal synchronization points and the cost of broadcasts. These tend
to slightly decrease the optimal value of NB_A.
- The model of communication adapter you are using. The High Performance
Switch Adapter-2 allows a larger NB.
- Load balancing. For the best processor utilization, it is necessary for
the processor nodes to be active for as long as possible; therefore, each one
should have as many blocks as possible. For a given problem size, this tends
to decrease the optimal value of NB_A (best load balancing: 1) and is
most relevant at very small problem sizes.
- If NB_A is equal to a power of 2, performance may be degraded.
- Use the following rules of thumb for reasonably-sized problems:
- For the POWER processors, choose NB_A in the following range:
- For PDPOTRF, use [30, 50], avoiding 32.
- For PZPOTRF, use [10, 25], avoiding 16.
- For the POWER2 processors, choose NB_A in the following range:
- For PDPOTRF, use [60, 80], avoiding 64.
- For PZPOTRF, use [20, 40], avoiding 32.
Matrix A is not positive definite. For
details, see the description of the info argument.
Unable to allocate work space
- DTYPE_A is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
- uplo <> 'U' or 'L'
- n < 0
- M_A < 0 and n = 0; M_A < 1
otherwise
- N_A < 0 and n = 0; N_A < 1
otherwise
- ia < 1
- ja < 1
- MB_A < 1
- NB_A < 1
- RSRC_A < 0 or RSRC_A >= p
- CSRC_A < 0 or CSRC_A >= q
If n <> 0:
- ia > M_A
- ja > N_A
- ia+n-1 > M_A
- ja+n-1 > N_A
In all cases:
- MB_A <> NB_A
- mod(ia-1, MB_A) <> mod(ja-1, NB_A)
- mod(ia-1, MB_A) <> 0
- LLD_A < max(1, LOCp(M_A))
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- ia differs.
- ja differs.
- DTYPE_A differs.
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
This example factors a 9 × 9
positive definite real symmetric matrix using a 2 × 2 process
grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N A IA JA DESC_A INFO
| | | | | | |
CALL PDPOTRF( 'L' , 9 , A , 1 , 1 , DESC_A , INFO )
| Desc_A
|
| DTYPE_
| 1
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| N_
| 9
|
| MB_
| 3
|
| NB_
| 3
|
| RSRC_
| 0
|
| CSRC_
| 0
|
| LLD_
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
In this example, LLD_A = 6 on P00 and P01,
and LLD_A = 3 on P10 and P11.
|
|
Global real symmetric matrix A of order 9 with block size
3 × 3:
B,D 0 1 2
* *
| 1.0 . . | . . . | . . . |
0 | 1.0 2.0 . | . . . | . . . |
| 1.0 2.0 3.0 | . . . | . . . |
| ----------------|------------------|---------------- |
| 1.0 2.0 3.0 | 4.0 . . | . . . |
1 | 1.0 2.0 3.0 | 4.0 5.0 . | . . . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | . . . |
| ----------------|------------------|---------------- |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 . . |
2 | 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 9.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------|-----------------
| 1.0 . . . . . | . . .
| 1.0 2.0 . . . . | . . .
| 1.0 2.0 3.0 . . . | . . .
0 | 1.0 2.0 3.0 7.0 . . | 4.0 5.0 6.0
| 1.0 2.0 3.0 7.0 8.0 . | 4.0 5.0 6.0
| 1.0 2.0 3.0 7.0 8.0 9.0 | 4.0 5.0 6.0
-----|--------------------------------|-----------------
| 1.0 2.0 3.0 . . . | 4.0 . .
1 | 1.0 2.0 3.0 . . . | 4.0 5.0 .
| 1.0 2.0 3.0 . . . | 4.0 5.0 6.0
Output:
Global real symmetric matrix A of order 9 with block size
3 × 3:
B,D 0 1 2
* *
| 1.0 . . | . . . | . . . |
0 | 1.0 1.0 . | . . . | . . . |
| 1.0 1.0 1.0 | . . . | . . . |
| ----------------|------------------|---------------- |
| 1.0 1.0 1.0 | 1.0 . . | . . . |
1 | 1.0 1.0 1.0 | 1.0 1.0 . | . . . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . . |
| ----------------|------------------|---------------- |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . . |
2 | 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------|-----------------
| 1.0 . . . . . | . . .
| 1.0 1.0 . . . . | . . .
| 1.0 1.0 1.0 . . . | . . .
0 | 1.0 1.0 1.0 1.0 . . | 1.0 1.0 1.0
| 1.0 1.0 1.0 1.0 1.0 . | 1.0 1.0 1.0
| 1.0 1.0 1.0 1.0 1.0 1.0 | 1.0 1.0 1.0
-----|--------------------------------|-----------------
| 1.0 1.0 1.0 . . . | 1.0 . .
1 | 1.0 1.0 1.0 . . . | 1.0 1.0 .
| 1.0 1.0 1.0 . . . | 1.0 1.0 1.0
The value of info is 0 on all processes.
This example factors a 9 × 9
positive definite complex Hermitian matrix using a 2 × 2 process
grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N A IA JA DESC_A INFO
| | | | | | |
CALL PZPOTRF( 'L' , 9 , A , 1 , 1 , DESC_A , INFO )
| Desc_A
|
| DTYPE_
| 1
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| N_
| 9
|
| MB_
| 3
|
| NB_
| 3
|
| RSRC_
| 0
|
| CSRC_
| 0
|
| LLD_
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
In this example, LLD_A = 6 on P00 and P01,
and LLD_A = 3 on P10 and P11.
|
|
Global complex Hermitian matrix A of order 9 with block size
3 × 3:
B,D 0 1 2
* *
| (18.0, . ) . . | . . . | . . . |
0 | (1.0, 1.0) (18.0, . ) . | . . . | . . . |
| (1.0, 1.0) (3.0, 1.0) (18.0, . ) | . . . | . . . |
| --------------------------------------|----------------------------------------|-------------------------------------- |
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (18.0, . ) . . | . . . |
1 | (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (7.0, 1.0) (18.0, . ) . | . . . |
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (7.0, 1.0) (9.0, 1.0) (18.0, . ) | . . . |
| --------------------------------------|----------------------------------------|-------------------------------------- |
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0) | (18.0, . ) . . |
2 | (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0) | (13.0, 1.0) (18.0, . ) . |
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0) | (13.0, 1.0) (15.0, 1.0) (18.0, . ) |
* *
| Note: |
On input, the imaginary parts of the diagonal elements of the complex
Hermitian matrix A are assumed to be zero, so you do not have to
set these values.
|
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
Local arrays for A:
p,q | 0 | 1
-----|--------------------------------------------------------------------------------|-----------------------------------------
| (18.0, . ) . . . . . | . . .
| (1.0, 1.0) (18.0, . ) . . . . | . . .
| (1.0, 1.0) (3.0, 1.0) (18.0, . ) . . . | . . .
0 | (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) (18.0, . ) . . | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0)
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) (13.0, 1.0) (18.0, . ) . | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0)
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) (13.0, 1.0) (15.0, 1.0) (18.0, . ) | (7.0, 1.0) (9.0, 1.0) (11.0, 1.0)
-----|--------------------------------------------------------------------------------|-----------------------------------------
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) . . . | (18.0, . ) . .
1 | (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) . . . | (7.0, 1.0) (18.0, . ) .
| (1.0, 1.0) (3.0, 1.0) (5.0, 1.0) . . . | (7.0, 1.0) (9.0, 1.0) (18.0, . )
Output:
Global complex Hermitian matrix A of order 9 with block size
3 × 3:
B,D 0 1 2
* *
| (4.2, 0.0) . . | . . . | . . . |
0 | (0.24, 0.24) (4.2, 0.0) . | . . . | . . . |
| (0.24, 0.24) (0.68, 0.24) (4.2, 0.0) | . . . | . . . |
| -----------------------------------------|-------------------------------------------|----------------------------------------- |
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (4.0, 0.0) . . | . . . |
1 | (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (1.3, 0.25) (3.8, 0.0) . | . . . |
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (1.3, 0.25) (1.4, 0.26) (3.5, 0.0) | . . . |
| -----------------------------------------|-------------------------------------------|----------------------------------------- |
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28) | (3.2, 0.0) . . |
2 | (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28) | (1.6, 0.32) (2.7, 0.0) . |
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28) | (1.6, 0.32) (1.6, 0.37) (2.2, 0.0) |
* *
| Note: |
On output, the imaginary parts of the diagonal elements of the matrix are set
to zero.
|
The following is the 2 × 2 process grid:
| B,D
| 0 2
| 1
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
Local arrays for A:
p,q | 0 | 1
-----|---------------------------------------------------------------------------------|------------------------------------------
| (4.2, 0.0) . . . . . | . . .
| (0.24, 0.24) (4.2, 0.0) . . . . | . . .
| (0.24, 0.24) (0.68, 0.24) (4.2, 0.0) . . . | . . .
0 | (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) (3.2, 0,0) . . | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28)
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) (1.6, 0.32) (2.7, 0.0) . | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28)
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) (1.6, 0.32) (1.6, 0.37) (2.2, 0.0) | (1.3, 0.25) (1.4, 0.26) (1.5, 0.28)
-----|---------------------------------------------------------------------------------|------------------------------------------
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) . . . | (4.0, 0.0) . .
1 | (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) . . . | (1.3, 0.25) (3.8, 0.0 .
| (0.24, 0.24) (0.68, 0.24) (1.1, 0.24) . . . | (1.3, 0.25) (1.4, 0.26) (3.5, 0.0)
The value of info is 0 on all processes.
These subroutines solve the following systems of equations for multiple
right-hand sides:
- AX = B
where, in the formula above:
- A represents the global positive definite real symmetric or
complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 factored by Cholesky
factorization.
- B represents the global general submatrix
Bib:ib+n-1,
jb:jb+nrhs-1 containing the
right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
jb:jb+nrhs-1 containing the
solution vectors in its columns.
This subroutine uses the results of the factorization of matrix
A, produced by a preceding call to PDPOTRF or PZPOTRF,
respectively. For details on the factorization, see PDPOTRF and PZPOTRF--Positive Definite Real Symmetric or Complex Hermitian Matrix Factorization.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
references [16], [18], [22], [36],
and [37].
Table 61. Data Types
| A, B
| Subroutine
|
| Long-precision real
| PDPOTRS
|
| Long-precision complex
| PZPOTRS
|
| Fortran
| CALL PDPOTRS | PZPOTRS (uplo, n, nrhs,
a, ia, ja, desc_a, b,
ib, jb, desc_b, info)
|
| C and C++
| pdpotrs | pzpotrs (uplo, n, nrhs, a,
ia, ja, desc_a, b, ib,
jb, desc_b, info);
|
- uplo
- indicates whether the upper or lower triangular part of the global real
symmetric or complex Hermitian submatrix A is referenced,
where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character; uplo = 'U'
or 'L'.
- n
- is the order of the factored matrix A.
Scope: global
Specified as: a fullword integer; n >= 0.
- nrhs
- is the number of right-hand sides-- that is, the number of columns
in submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- a
- is the local part of the global real symmetric or complex Hermitian matrix
A, containing the factorization of matrix A produced by
a preceding call to PDPOTRF or PZPOTRF, respectively. This identifies the
first element of the local array A. This subroutine
computes the location of the first element of the local subarray used, based
on ia, ja, desc_a, p, q,
myrow, and mycol; therefore, the leading
LOCp(ia+n-1) by LOCq(ja+n-1)
part of the local array A must contain the local pieces of the
leading ia+n-1 by ja+n-1 part
of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global real
symmetric or complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global real
symmetric or complex Hermitian submatrix
Aia:ia+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least) LOCq(N_A) array, containing
numbers of the data type indicated in Table 61. Details about the square block-cyclic data distribution of global matrix
A are stored in desc_a.
- ia
- is the row index of the global matrix A, identifying the first
row of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ia <= M_A and
ia+n-1 <= M_A.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, described in the
following table:
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A=1
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_A < q
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= max(1,LOCp(M_A))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, jb, desc_b, p, q,
myrow, and mycol; therefore, the leading
LOCp(ib+n-1) by
LOCq(jb+nrhs-1) part of the local array B
must contain the local pieces of the leading ib+n-1 by
jb+nrhs-1 part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) LOCq(N_B) array, containing
numbers of the data type indicated in Table 61. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- jb
- is the column index of the global matrix B, identifying the
first column of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= jb <= N_B and
jb+nrhs-1 <= N_B.
- desc_b
- is the array descriptor for global matrix B, described in the
following table:
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B=1
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0 or nrhs = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
|
If n = 0 or nrhs = 0:
N_B >= 0
Otherwise:
N_B >= 1
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row of the p × q grid over
which the first row of the global matrix is distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column of the p × q grid over
which the first column of the global matrix is distributed
| 0 <= CSRC_B < q
| Global
|
| 9
| LLD_B
| The leading dimension of the local array
| LLD_B >= max(1,LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- info
- See 'On Return'.
- b
- is the updated local part of the global matrix B, containing
the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) LOCq(N_B) array, containing
numbers of the data type indicated in Table 61.
- info
- indicates that a successful computation occurred.
Scope: global
Returned as: a fullword integer; info = 0.
- In your C program, argument info must be passed by reference.
- This subroutine accepts lowercase letters for the uplo argument.
- The matrices must have no common elements; otherwise, results are
unpredictable.
- The scalar data specified for input argument n must be the same
for both PDPOTRF/PZPOTRF and PDPOTRS/PZPOTRS.
- The global submatrix A input to PDPOTRS/PZPOTRS must
be the same as for the corresponding output argument for
PDPOTRF/PZPOTRS; and thus, the scalar data specified for ia,
ja, and the contents of desc_a must also be the same.
- The NUMROC utility subroutine can be used to determine the values of
LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details,
see "Determining the Number of Rows and Columns in Your Local Arrays" and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
- For suggested block sizes, see "Coding Tips for Optimizing Parallel Performance".
- On both input and output, matrices A and B conform
to ScaLAPACK format.
- The following values must be equal: CTXT_A = CTXT_B.
- The global real symmetric or complex Hermitian matrix A must be
distributed using a square block-cyclic distribution; that is,
MB_A = NB_A.
- The following block sizes must be equal: MB_A = MB_B.
- The global real symmetric or complex Hermitian matrix A must be
aligned on a block row boundary; that is, ia-1 must be a
multiple of MB_A.
- The block row offset of A must be equal to the block column
offset of A; that is, mod(ia-1,
MB_A) = mod(ja-1, NB_A).
- The block row offset of A must be equal to the block row offset
of B; that is, mod(ia-1,
MB_A) = mod(ib-1, MB_B).
- In the process grid, the process row containing the first row of the
submatrix A must also contain the first row of the submatrix
B; that is, iarow = ibrow, where:
- iarow = mod((((ia-1)/MB_A)+RSRC_A),
p)
- ibrow = mod((((ib-1)/MB_B)+RSRC_B),
p)
None
| Note: |
If the factorization performed by PDPOTRF/PZPOTRF failed because of a
nonpositive definite matrix A, the results returned by this
subroutine are unpredictable. For details, see the info output
argument for PDPOTRF/PZPOTRF.
|
Unable to allocate work space
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
- uplo <> 'U' or 'L'
- n < 0
- nrhs < 0
- M_A < 0 and n = 0; M_A < 1
otherwise
- N_A < 0 and n = 0; N_A < 1
otherwise
- ia < 1
- ja < 1
- MB_A < 1
- NB_A < 1
- RSRC_A < 0 or RSRC_A >= p
- CSRC_A < 0 or CSRC_A >= q
- M_B < 0 and (n = 0 or
nrhs = 0); M_B < 1 otherwise
- N_B < 0 and (n = 0 or
nrhs = 0); N_B < 1 otherwise
- ib < 1
- jb < 1
- MB_B < 1
- NB_B < 1
- RSRC_B < 0 or RSRC_B >= p
- CSRC_B < 0 or CSRC_B >= q
- CTXT_A <> CTXT_B
If n <> 0:
- ia > M_A
- ja > N_A
- ia+n-1 > M_A
- ja+n-1 > N_A
If n <> 0 and nrhs <> 0:
- ib > M_B
- jb > N_B
- ib+n-1 > M_B
- jb+nrhs-1 > N_B
In all cases:
- MB_A <> NB_A
- mod(ia-1, MB_A) <> mod(ja-1, NB_A)
- MB_B <> MB_A
- mod(ia-1, MB_A) <> mod(ib-1,
MB_B).
- mod(ia-1, MB_A) <> 0
- In the process grid, the process row containing the first row of the
submatrix A does not contain the first row of the submatrix
B; that is, iarow <> ibrow,
where:
- iarow = mod((((ia-1)/MB_A)+RSRC_A),
p)
- ibrow = mod((((ib-1)/MB_B)+RSRC_B),
p)
- LLD_A < max(1, LOCp(M_A))
- LLD_B < max(1, LOCp(M_B))
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- nrhs differs.
- ia differs.
- ja differs.
- DTYPE_A differs.
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
- ib differs.
- jb differs.
- DTYPE_B differs.
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
This example solves the positive definite
real symmetric system AX = B with 5 right-hand
sides using a 2 × 2 process grid. The transformed matrix
A is the output from "Example 1".
This example uses a global submatrix B within a global matrix
B by specifying ib = 1 and
jb = 2.
By specifying CSRC_B = 1, the columns of global matrix B
are distributed over the process grid starting in the second column of the
process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N NRHS A IA JA DESC_A B IB JB DESC_B INFO
| | | | | | | | | | | |
CALL PDPOTRS( 'L' , 9 , 5 , A , 1 , 1 , DESC_A , B , 1 , 2 , DESC_B , INFO )
| Desc_A
| Desc_B
|
| DTYPE_
| 1
| 1
|
| CTXT_
| icontxt1
| icontxt1
|
| M_
| 9
| 9
|
| N_
| 9
| 6
|
| MB_
| 3
| 3
|
| NB_
| 3
| 2
|
| RSRC_
| 0
| 0
|
| CSRC_
| 0
| 1
|
| LLD_
| See below2
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW))
In this example, LLD_A = LLD_B = 6 on P00 and
P01, and LLD_A = LLD_B = 3 on P10 and
P11.
|
|
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . 18.0 | 27.0 36.0 | 45.0 9.0 |
0 | . 34.0 | 51.0 68.0 | 85.0 17.0 |
| . 48.0 | 72.0 96.0 | 120.0 24.0 |
| ---------------|-----------------|--------------- |
| . 60.0 | 90.0 120.0 | 150.0 30.0 |
1 | . 70.0 | 105.0 140.0 | 175.0 35.0 |
| . 78.0 | 117.0 156.0 | 195.0 39.0 |
| ---------------|-----------------|--------------- |
| . 84.0 | 126.0 168.0 | 210.0 42.0 |
2 | . 88.0 | 132.0 176.0 | 220.0 44.0 |
| . 90.0 | 135.0 180.0 | 225.0 45.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
| Note: |
The first column of B begins in the second column of the process
grid.
|
Local arrays for B:
p,q | 0 | 1
-----|----------------|------------------------------
| 27.0 36.0 | . 18.0 45.0 9.0
| 51.0 68.0 | . 34.0 85.0 17.0
| 72.0 96.0 | . 48.0 120.0 24.0
0 | 126.0 168.0 | . 84.0 210.0 42.0
| 132.0 176.0 | . 88.0 220.0 44.0
| 135.0 180.0 | . 90.0 225.0 45.0
-----|----------------|------------------------------
| 90.0 120.0 | . 60.0 150.0 30.0
1 | 105.0 140.0 | . 70.0 175.0 35.0
| 117.0 156.0 | . 78.0 195.0 39.0
Output:
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
0 | . 2.0 | 3.0 4.0 | 5.0 1.0 |
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
| -----------|-------------|----------- |
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
1 | . 2.0 | 3.0 4.0 | 5.0 1.0 |
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
| -----------|-------------|----------- |
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
2 | . 2.0 | 3.0 4.0 | 5.0 1.0 |
| . 2.0 | 3.0 4.0 | 5.0 1.0 |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
| Note: |
The first column of B begins in the second column of the process
grid.
|
Local arrays for B:
p,q | 0 | 1
-----|------------|----------------------
| 3.0 4.0 | . 2.0 5.0 1.0
| 3.0 4.0 | . 2.0 5.0 1.0
| 3.0 4.0 | . 2.0 5.0 1.0
0 | 3.0 4.0 | . 2.0 5.0 1.0
| 3.0 4.0 | . 2.0 5.0 1.0
| 3.0 4.0 | . 2.0 5.0 1.0
-----|------------|----------------------
| 3.0 4.0 | . 2.0 5.0 1.0
1 | 3.0 4.0 | . 2.0 5.0 1.0
| 3.0 4.0 | . 2.0 5.0 1.0
The value of info is 0 on all processes.
This example solves the positive definite
complex Hermitian system AX = B with 5
right-hand sides using a 2 × 2 process grid. The transformed
matrix A is the output from "Example 2".
This example uses a global submatrix B within a global matrix
B by specifying ib = 1 and
jb = 2.
By specifying CSRC_B = 1, the columns of global matrix B
are distributed over the process grid starting in the second column of the
process grid.
ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N NRHS A IA JA DESC_A B IB JB DESC_B INFO
| | | | | | | | | | | |
CALL PZPOTRS( 'L' , 9 , 5 , A , 1 , 1 , DESC_A , B , 1 , 2 , DESC_B , INFO )
| Desc_A
| Desc_B
|
| DTYPE_
| 1
| 1
|
| CTXT_
| icontxt1
| icontxt1
|
| M_
| 9
| 9
|
| N_
| 9
| 6
|
| MB_
| 3
| 3
|
| NB_
| 3
| 2
|
| RSRC_
| 0
| 0
|
| CSRC_
| 0
| 1
|
| LLD_
| See below2
| See below2
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
2 Each process should set the LLD_ as follows:
LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW))
LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW))
In this example, LLD_A = LLD_B = 6 on P00 and
P01, and LLD_A = LLD_B = 3 on P10 and
P11.
|
|
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . (60.0, 10.0) | (86.0, 2.0) (112.0, -6.0) | (138.0, -14.0) (34.0, 18.0) |
0 | . (86.0, 28.0) | (126.0, 22.0) (166.0, 16.0) | (206.0, 10.0) (46.0, 34.0) |
| . (108.0, 44.0) | (160.0, 40.0) (212.0, 36.0) | (264.0, 32.0) (56.0, 48.0) |
| ---------------------------|-----------------------------------|-------------------------------- |
| . (126.0, 58.0) | (188.0, 56.0) (250.0, 54.0) | (312.0, 52.0) (64.0, 60.0) |
1 | . (140.0, 70.0) | (210.0, 70.0) (280.0, 70.0) | (350.0, 70.0) (70.0, 70.0) |
| . (150.0, 80.0) | (226.0, 82.0) (302.0, 84.0) | (378.0, 86.0) (74.0, 78.0) |
| ---------------------------|-----------------------------------|-------------------------------- |
| . (156.0, 88.0) | (236.0, 92.0) (316.0, 96.0) | (396.0, 100.0) (76.0, 84.0) |
2 | . (158.0, 94.0) | (240.0, 100.0) (322.0, 106.0) | (404.0, 112.0) (76.0, 88.0) |
| . (156.0, 98.0) | (238.0, 106.0) (320.0, 114.0) | (402.0, 122.0) (74.0, 90.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
| Note: |
The first column of B begins in the second column of the process
grid.
|
Local arrays for B:
p,q | 0 | 1
-----|----------------------------------|-----------------------------------------------------------
| (86.0, 2.0) (112.0, -6.0) | . (60.0, 10.0) (138.0, -14.0) (34.0, 18.0)
| (126.0, 22.0) (166.0, 16.0) | . (86.0, 28.0) (206.0, 10.0) (46.0, 34.0)
| (160.0, 40.0) (212.0, 36.0) | . (108.0, 44.0) (264.0, 32.0) (56.0, 48.0)
0 | (236.0, 92.0) (316.0, 96.0) | . (156.0, 88.0) (396.0, 100.0) (76.0, 84.0)
| (240.0, 100.0) (322.0, 106.0) | . (158.0, 94.0) (404.0, 112.0) (76.0, 88.0)
| (238.0, 106.0) (320.0, 114.0) | . (156.0, 98.0) (402.0, 122.0) (74.0, 90.0)
-----|----------------------------------|-----------------------------------------------------------
| (188.0, 56.0) (250.0, 54.0) | . (126.0, 58.0) (312.0, 52.0) (64.0, 60.0)
1 | (210.0, 70.0) (280.0, 70.0) | . (140.0, 70.0) (350.0, 70.0) (70.0, 70.0)
| (226.0, 82.0) (302.0, 84.0) | . (150.0, 80.0) (378.0, 86.0) (74.0, 78.0)
Output:
After the global matrix B is distributed over the process grid,
only a portion of the global data structure is used--that is, global
submatrix B. Following is the global 9 × 5 submatrix
B, starting at row 1 and column 2 in global general
9 × 6 matrix B with block size
3 × 2:
B,D 0 1 2
* *
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
0 | . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
| ------------------|---------------------------|------------------------- |
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
1 | . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
| ------------------|---------------------------|------------------------- |
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
2 | . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
| . (2.0, 1.0) | (3.0, 1.0) (4.0, 1.0) | (5.0, 1.0) (1.0, 1.0) |
* *
The following is the 2 × 2 process grid:
| B,D
| 1
| 0 2
|
| 0
2
| P00
| P01
|
| 1
| P10
| P11
|
| Note: |
The first column of B begins in the second column of the process
grid.
|
Local arrays for B:
p,q | 0 | 1
-----|--------------------------|-------------------------------------------
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
0 | (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
-----|--------------------------|-------------------------------------------
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
1 | (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
| (3.0, 4.0) (3.0, 4.0) | . (2.0, 1.0) (5.0, 1.0) (1.0, 1.0)
The value of info is 0 on all processes.
This section contains the banded linear algebraic equation subroutine
descriptions.
This subroutine solves the following system of equations for multiple
right-hand sides:
- AX = B
where, in the formula above:
- A represents the global positive definite symmetric band
submatrix Aja:ja+n-1,
ja:ja+n-1 to be factored by
Cholesky factorization.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
references [2], [23], [39], and [40].
Table 62. Data Types
| A, B, work
| Subroutine
|
| Long-precision real
| PDPBSV
|
| Fortran
| CALL PDPBSV (uplo, n, k, nrhs,
a, ja, desc_a, b, ib,
desc_b, work, lwork, info)
|
| C and C++
| pdpbsv (uplo, n, k, nrhs, a,
ja, desc_a, b, ib, desc_b,
work, lwork, info);
|
- uplo
- indicates whether the upper or lower triangular part of the global
submatrix A is referenced, where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character; uplo = 'U'
or 'L'.
- n
- is the number of columns in the submatrix A, stored in the
upper- or lower-band-packed storage mode. It is also the number of rows in the
general submatrix B containing the multiple right-hand sides.
Scope: global
Specified as: a fullword integer;
0 <= n <= (NB_A)p-mod(ja-1,NB_A).
- k
- is the half bandwidth of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If uplo = 'U',
0 <= k <= NB_A.
- If uplo = 'L',
0 <= k < n.
These limits for k are extensions of the ScaLAPACK standard.
- nrhs
- is the number of columns in submatrix B used in the
computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- a
- is the local part of the global positive definite symmetric band matrix
A, stored in upper- or lower-band-packed storage mode, to be
factored. This identifies the first element of the local array
A. This subroutine computes the location of the first element of
the local subarray used, based on k, ja, desc_a,
and p; therefore, the leading k+1 by
LOCp(ja+n-1) part of the local array A must
contain the local pieces of the leading k+1 by
ja+n-1 part of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 62. Details about the block-cyclic data distribution of global matrix
A are stored in desc_a.
On output, array A is overwritten; that is, original input is
not preserved.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, which may be type
501 or type 1, as described in the following tables. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| LLD_A
| Leading dimension
| LLD_A >= k+1
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A > k
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= k+1
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 62. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B=0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B)
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 62.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer, where:
- info
- See 'On Return'.
- a
- a is overwritten; that is, the original input is not preserved.
This subroutine overwrites data in positions that do not contain the positive
definite symmetric band matrix A stored in upper- or
lower-band-packed storage mode.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 62.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1, the
size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 62, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to the
optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite, and the factorization completed normally or the work area query
completed successfully.
If info > 0, the leading minor of order i of
the global submatrix A is not positive definite. info is
set equal to i, where the first leading minor was encountered at
Aja+i-1,
ja+i-1. The results contained in matrix
A are not defined.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- The subroutine accepts lowercase letters for the uplo argument.
- This subroutine gives the best performance for wide band widths, for
example:
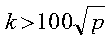
where p is the number of processes. For details, see references
[2], [39], and [40]. Also, it
is suggested that you specify uplo = 'L'.
- A, B, and work must have no common
elements; otherwise, results are unpredictable.
- In all cases, follow these rules:
- ib = ja
- DTYPE_A=501 or 1
- DTYPE_B=502 or 1
- NB_A = MB_B
- If DTYPE_A=1, RSRC_A=0, M_A >= k+1, and MB_A >= 1.
- If DTYPE_B=1, CSRC_B=0, N_B >= nrhs, and NB_B >= 1.
- CTXT_A = CTXT_B
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 501
| 1
| 1 × p
|
| 1
| 502
| p × 1
|
| 1
| 1
| 1 × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- The global band matrix A must be positive definite. If
A is not positive definite, this subroutine uses the info
argument to provide information about A and issues an error
message. This differs from ScaLAPACK, which only uses the info
argument to provide information about A.
- The global positive definite symmetric band matrix A must be
stored in upper- or lower-band-packed storage mode. See the section on
block-cyclically distributing a symmetric matrix in "Matrices".
Matrix A must be distributed over a one-dimensional process grid
using block-cyclic data distribution. For more information on using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrices A and B may be
block-cyclically distributed on a 1 × p or
p × 1 process grid, the values of n,
ja, ib, NB_A and MB_B, must be chosen so that each process
has at most one full or partial block of each of the global submatrices
A and B.
Matrix A is not positive definite
(corresponding computational error messages are issued by both PDPBTRF and
PDPBSV). For details, see the description of the info argument.
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- PDPBSV was called from outside the process grid.
- The process grid is not 1 × p or
p × 1.
- uplo <> 'U' or 'L'
- n < 0
- k < 0
- k+1 > n
- ja < 1
- DTYPE_A = 1 and:
- M_A < k+1
- MB_A < 1
- RSRC_A <> 0
- The process grid is not 1 × p.
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n+mod(ja-1,
NB_A) > (NB_A)p
- CSRC_A < 0 or CSRC_A >= p
- uplo = 'U' and k > NB_A
- nrhs < 0
- ib <> ja
- ib < 1
- DTYPE_B = 1 and:
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
- The process grid is not p × 1.
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- n+mod(ib-1,MB_B) > (MB_B)p
- MB_B <> NB_A
- RSRC_B < 0 or RSRC_B >= p
- CTXT_A <> CTXT_B
If n <> 0:
- ja+n-1 > N_A
- ja > N_A
- ib > M_B
- ib+n-1 > M_B
- LLD_A < k+1
- LLD_B < max(1, LOCp(M_B))
- lwork <> 0, lwork <> -1, and
lwork < (NB_A+2k)(k)+max(nrhs,
k)(k)
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- k differs.
- nrhs differs.
- ja differs.
- DTYPE_A differs.
- DTYPE_A does not differ and:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
- DTYPE_A = 1 and:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
- ib differs.
- DTYPE_B differs.
- DTYPE_B does not differ and:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
- DTYPE_A = 1 and:
- N_B differs.
- NB_B differs.
- CSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
positive definite symmetric band matrix A of order 9 with a half
bandwidth of 7:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 1.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 2.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 3.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 7.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 |
* *
Matrix A is stored in lower-band-packed storage mode:
* *
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 . |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 . . |
| 1.0 2.0 3.0 4.0 5.0 5.0 . . . |
| 1.0 2.0 3.0 4.0 4.0 . . . . |
| 1.0 2.0 3.0 3.0 . . . . . |
| 1.0 2.0 2.0 . . . . . . |
| 1.0 1.0 . . . . . . . |
* *
where "." means you do not have to store a value in that
position in the local array. However, these storage positions are required and
are overwritten during the computation.
Notes:
- On output, the submatrix A is overwritten; that is, the
original input is not preserved.
- Notice only one process grid was created, even though,
DTYPE_A = 501 and DTYPE_B = 502.
- Because lwork = 0, PDPBSV dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N K NRHS A JA DESC_A B IB DESC_B WORK LWORK INFO
| | | | | | | | | | | | |
CALL PDPBSV( 'L' , 9 , 7 , 3 , A , 1 , DESC_A , B , 1 , DESC_B , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt1
|
| N_
| 9
|
| NB_
| 3
|
| CSRC_
| 0
|
| LLD_A
| 8
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| MB_
| 3
|
| RSRC_
| 0
|
| LLD_B
| 3
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global matrix A stored in lower-band-packed storage mode with
block size of 3:
B,D 0 1 2
* *
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0 |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . . |
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . . |
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . . |
| 1.0 2.0 3.0 | 3.0 . . | . . . |
| 1.0 2.0 2.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 .
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . .
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . .
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . .
| 1.0 2.0 3.0 | 3.0 . . | . . .
| 1.0 2.0 2.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
Global matrix B with block size of 3:
B,D 0
* *
| 8.0 36.0 44.0 |
0 | 16.0 80.0 80.0 |
| 23.0 122.0 108.0 |
| ----------------- |
| 29.0 161.0 129.0 |
1 | 34.0 196.0 144.0 |
| 38.0 226.0 154.0 |
| ----------------- |
| 41.0 250.0 160.0 |
2 | 43.0 267.0 163.0 |
| 36.0 240.0 120.0 |
* *
The following is the 1 × 3 process grid:
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|--------------------|---------------------|--------------------
| 8.0 36.0 44.0 | 29.0 161.0 129.0 | 41.0 250.0 160.0
0 | 16.0 80.0 80.0 | 34.0 196.0 144.0 | 43.0 267.0 163.0
| 23.0 122.0 108.0 | 38.0 226.0 154.0 | 36.0 240.0 120.0
Output:
Global matrix B with block size of 3:
B,D 0
* *
| 1.0 1.0 9.0 |
0 | 1.0 2.0 8.0 |
| 1.0 3.0 7.0 |
| -------------- |
| 1.0 4.0 6.0 |
1 | 1.0 5.0 5.0 |
| 1.0 6.0 4.0 |
| -------------- |
| 1.0 7.0 3.0 |
2 | 1.0 8.0 2.0 |
| 1.0 9.0 1.0 |
* *
The following is the 1 × 3 process grid:
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 9.0 | 1.0 4.0 6.0 | 1.0 7.0 3.0
0 | 1.0 2.0 8.0 | 1.0 5.0 5.0 | 1.0 8.0 2.0
| 1.0 3.0 7.0 | 1.0 6.0 4.0 | 1.0 9.0 1.0
The value of info is 0 on all processes.
This subroutine uses Cholesky factorization to factor a positive definite
symmetric band matrix A, stored in upper- or lower-band-packed
storage mode, into one of the following forms:
- A = UTU if
A is upper triangular.
- A = LLT if A is lower
triangular.
where, in the formulas above:
- A represents the global positive definite symmetric band
submatrix Aja:ja+n-1,
ja:ja+n-1 to be factored.
- U is an upper triangular matrix.
- L is a lower triangular matrix.
To solve the system of equations with multiple right-hand sides, follow the
call to this subroutine with one of more calls to PDPBTRS. The output from
this factorization subroutine should be used only as input to PDPBTRS.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See references [2], [23], [39], and [40].
Table 63. Data Types
| A, af, work
| Subroutine
|
| Long-precision real
| PDPBTRF
|
| Fortran
| CALL PDPBTRF (uplo, n, k, a,
ja, desc_a, af, laf, work,
lwork, info)
|
| C and C++
| pdpbtrf (uplo, n, k, a, ja,
desc_a, af, laf, work, lwork,
info);
|
- uplo
- indicates whether the upper or lower triangular part of the global
submatrix A is referenced, where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character; uplo = 'U'
or 'L'.
- n
- is the number of columns in the submatrix A, stored in upper-
or lower-band-packed storage mode, to be factored.
Scope: global
Specified as: a fullword integer;
0 <= n <= (NB_A)p-mod(ja-1,NB_A).
- k
- is the half bandwidth of the submatrix A to be factored.
Scope: global
Specified as: a fullword integer, where:
- If uplo = 'U',
0 <= k <= NB_A.
- If uplo = 'L',
0 <= k < n.
These limits for k are extensions of the ScaLAPACK standard.
- a
- is the local part of the global positive definite symmetric band matrix
A, stored in upper- or lower-band-packed storage mode, to be
factored. This identifies the first element of the local array
A. This subroutine computes the location of the first element of
the local subarray used, based on k, ja, desc_a,
and p; therefore, the leading k+1 by
LOCp(ja+n-1) part of the local array A must
contain the local pieces of the leading k+1 by
ja+n-1 part of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 63. Details about the block-cyclic data distribution of global matrix
A are stored in desc_a.
On output, array A is overwritten; that is, original input is
not preserved.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, which may be type
501 or type 1, as described in the following tables.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| LLD_A
| Leading dimension
| LLD_A >= k+1
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A > k
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= k+1
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- is a reserved output area and its size is specified by LAF.
Scope: local
Specified as: for migration purposes, you should specify a
one-dimensional, long-precision array of (at least) length LAF.
- laf
- is the number of elements in array AF.
The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, you should specify
laf using the formula below.
Scope: local
Specified as: a fullword integer,
laf >= (NB_A+2k)(k).
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 63.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDPBTRF dynamically allocates the work area
used by this subroutine. The work area is deallocated before control is
returned to the calling program. This option is an extension to the ScaLAPACK
standard. It is suggested that you specify lwork=0.
- If lwork = -1, PDPBTRF performs a work area query and
returns the optimum required size of work in
work1. No computation is performed and the subroutine
returns after error checking is complete.
- Otherwise, it must have the following value:
lwork >= k2
- info
- See 'On Return'.
- a
- a is the updated local part of the global matrix A,
containing the results of the factorization, where:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the results of
the factorization. The remaining elements stored in submatrix A
were overwritten by this subroutine.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the results of
the factorization. The remaining elements stored in submatrix A
were overwritten by this subroutine.
Scope: local
Returned as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 63.
On output, array A is overwritten; that is, original input is
not preserved.
- af
- is a reserved area.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 or lwork <> -1, the
size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 63, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to the
optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite and the factorization completed normally, or the work area query
completed successfully.
If info > 0, the leading minor of order i of
the global submatrix A is not positive definite. info is
set equal to i, where the first leading minor was encountered at
Aja+i-1,
ja+i-1. The results contained in matrix
A are not defined.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- This subroutine accepts lowercase letters for the uplo argument.
- This subroutine gives the best performance for wide band widths, for
example:
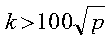
where p is the number of processes. For details, see references
[2], [39], and [40]. Also, it
is suggested that you specify uplo = 'L'.
- The k+1 by n array specified for submatrix A
must remain unchanged between calls to PDPBTRF and PDPBTRS. This subroutine
overwrites data in positions that do not contain the positive definite
symmetric band matrix A stored in upper- or lower-band-packed
storage mode.
- The output from this factorization subroutine should be used only as input
to the solve subroutine PDPBTRS.
The data specified for input arguments uplo, n, and
k must be the same for both PDPBTRF and PDPBTRS.
The matrix A and af input to PDPBTRS must be the same
as the corresponding output arguments for PDPBTRF; and thus, the scalar data
specified for ja, desc_a, and laf must also be the
same.
- In all cases, follow these rules:
- DTYPE_A=501 or 1
- If DTYPE_A=1, RSRC_A=0, M_A >= k+1, and MB_A >= 1.
- Following are the allowable array descriptor types and process grids,
where p is the number of processes in the process grid:
| DTYPE_A
| Process Grid
|
| 501
| p × 1 or 1 × p
|
| 1
| 1 × p
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- Matrix A, af, and work must have no common
elements; otherwise, results are unpredictable.
- The global symmetric band matrix A must be positive definite.
If A is not positive definite, this subroutine uses the
info argument to provide information about A and issues an
error message. This differs from ScaLAPACK, which only uses the info
argument to provide information about A.
- The global positive definite symmetric band matrix A must be
stored in upper- or lower-band-packed storage mode. See the section on
block-cyclically distributing a symmetric matrix in "Matrices".
Matrix A must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrix A may be block-cyclically distributed on
a 1 × p or p × 1 process grid,
the values of n, ja, and NB_A must be chosen so that each
process has at most one full or partial block of the global submatrix
A.
Matrix A is not positive definite. For
details, see the description of the info argument.
lwork= 0 and unable to allocate workspace
- DTYPE_A is invalid.
- CTXT_A is invalid.
- PDPBTRF was called from outside the process grid.
- The process grid is not 1 × p or
p × 1.
- uplo <> 'U' or 'L'
- n < 0
- ja < 1
- k < 0
- k+1 > n
- DTYPE_A = 1 and:
- M_A < k+1
- MB_A < 1
- RSRC_A <> 0
- The process grid is not 1 × p.
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)p-mod(ja-1,NB_A)
- CSRC_A < 0 or CSRC_A >= p
- uplo = 'U' and k > NB_A.
- ja > N_A and (n > 0)
- ja+n-1 > N_A and
(n > 0)
- LLD_A < k+1
- lwork <> 0, lwork <> -1, and
lwork < k2
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- k differs.
- ja differs.
- DTYPE_A differs.
- DTYPE_A does not differ and:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
- DTYPE_A = 1 and:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
positive definite symmetric band matrix A of order 9 with a half
bandwidth of 7:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 1.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 2.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 3.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 7.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 |
* *
Matrix A is stored in lower-band-packed storage mode:
* *
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 . |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 . . |
| 1.0 2.0 3.0 4.0 5.0 5.0 . . . |
| 1.0 2.0 3.0 4.0 4.0 . . . . |
| 1.0 2.0 3.0 3.0 . . . . . |
| 1.0 2.0 2.0 . . . . . . |
| 1.0 1.0 . . . . . . . |
* *
where "." means you do not have to store a value in that
position in the local array. However, these storage positions are required and
are overwritten during the computation.
Matrix A is distributed over a 1 × 3 process grid
using block-cyclic distribution.
Notes:
- Matrix A, output from PDPBTRF, must be passed, unchanged, to
the solve subroutine PDPBTRS.
- The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, in this example,
laf is specified as 119.
- The af argument is reserved and not shown in this example.
- Because lwork = 0, PDPBTRF dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N K A JA DESC_A AF LAF WORK LWORK INFO
| | | | | | | | | | |
CALL PDPBTRF( 'L' , 9 , 7 , A , 1 , DESC_A , AF , 119 , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt1
|
| N_
| 9
|
| NB_
| 3
|
| CSRC_
| 0
|
| LLD_A
| 8
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global matrix A stored in lower-band-packed storage mode with
block size of 3:
B,D 0 1 2
* *
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0 |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . . |
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . . |
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . . |
| 1.0 2.0 3.0 | 3.0 . . | . . . |
| 1.0 2.0 2.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 .
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . .
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . .
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . .
| 1.0 2.0 3.0 | 3.0 . . | . . .
| 1.0 2.0 2.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
Output:
Global matrix A is returned in lower-band-packed storage mode
with block size of 3:
B,D 0 1 2
* *
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0 |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . . |
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . . |
| 1.0 1.0 1.0 | 1.0 . . | . . . |
| 1.0 1.0 1.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . .
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . .
| 1.0 1.0 1.0 | 1.0 . . | . . .
| 1.0 1.0 1.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
The value of info is 0 on all processes.
This subroutine solves the following system of equations for multiple
right-hand sides:
- AX = B
where, in the formula above:
- A represents the global positive definite symmetric band
submatrix Aja:ja+n-1,
ja:ja+n-1 factored by Cholesky
factorization.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
This subroutine uses the results of the factorization of matrix
A, produced by a preceding call to PDPBTRF. The output from PDPBTRF
should be used only as input to this solve subroutine.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
references [2], [23], [39], and [40].
Table 64. Data Types
| A, B, af, work
| Subroutine
|
| Long-precision real
| PDPBTRS
|
| Fortran
| CALL PDPBTRS (uplo, n, k, nrhs,
a, ja, desc_a, b, ib,
desc_b, af, laf, work, lwork,
info)
|
| C and C++
| pdpbtrs (uplo, n, k, nrhs,
a, ja, desc_a, b, ib,
desc_b, af, laf, work, lwork,
info);
|
- uplo
- indicates whether the upper or lower triangular part of the global
submatrix A is referenced, where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character; uplo = 'U'
or 'L'.
- n
- is the number of columns in the submatrix A, stored in the
upper- or lower-band-packed storage mode. It is also the number of rows in the
general submatrix B containing the multiple right-hand sides.
Scope: global
Specified as: a fullword integer;
0 <= n <= (NB_A)p-mod(ja-1,NB_A).
- k
- is the half bandwidth of the factored submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If uplo = 'U',
0 <= k <= NB_A.
- If uplo = 'L',
0 <= k < n.
These limits for k are extensions of the ScaLAPACK standard.
- nrhs
- is the number of columns in submatrix B used in the
computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- a
- is the local part of the global positive definite symmetric band matrix
A, stored in upper- or lower-band-packed storage mode, containing
the factorization of matrix A produced from a preceding call to
PDPBTRF. This identifies the first element of the local array
A. This subroutine computes the location of the first element of
the local subarray used, based on k, ja, desc_a,
and p; therefore, the leading k+1 by
LOCp(ja+n-1) part of the local array A must
contain the local pieces of the leading k+1 by
ja+n-1 part of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the
factorization.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the
factorization.
Scope: local
Specified as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 64. Details about the block-cyclic data distribution of global matrix
A are stored in desc_a.
On output, array A is overwritten; that is, original input is
not preserved.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, which may be type
501 or type 1, as described in the following tables. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| LLD_A
| Leading dimension
| LLD_A >= k+1
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A > k
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= k+1
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 64. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B=0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- is a reserved area. Its size is specified by LAF.
Scope: local
Specified as: for migration purposes, you should specify a
one-dimensional, long-precision array of (at least) length laf.
- laf
- is the number of elements in array AF.
The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, you should specify
laf using the formula below.
Scope: local
Specified as: a fullword integer,
laf >= (NB_A+2k)(k).
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 64.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDPBTRS dynamically allocates the work area
used by the subroutine. The work area is deallocated before control is
returned to the calling program. This option is an extension to the ScaLAPACK
standard. It is suggested that you specify lwork=0.
- If lwork = -1, PDPBTRS performs a work area query and
returns the optimum required size of work in
work1. No computation is performed and the subroutine
returns after error checking is complete.
- Otherwise,
lwork >= (nrhs)(k)
- info
- See 'On Return'.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 64.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 or lwork <> -1, the
size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 64, where:
- If lwork = -1, work1 is set to the
optimum lwork value needed.
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- indicates a successful computation or work area query occurred.
Scope: global
Returned as: a fullword integer; info = 0.
- In your C program, argument info must be passed by reference.
- The subroutine accepts lowercase letters for the uplo argument.
- This subroutine gives the best performance for wide band widths, for
example:
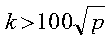
where p is the number of processes). For details, see references
[2], [39], and [40]. Also, it
is suggested that you specify uplo = 'L'.
- The k+1 by n array specified for submatrix A
must remain unchanged between calls to PDPBTRF and PDPBTRS. This subroutine
overwrites data in positions that do not contain the positive definite
symmetric band matrix A stored in upper- or lower-band-packed
storage mode.
- The output from the PDPBTRF subroutine should be used only as input to the
solve subroutine PDPBTRS.
The input arguments uplo, n, and k must be the
same for both PDPBTRF and PDPBTRS.
The global matrix A and af input to PDPBTRS must be the
same as the corresponding output arguments for PDPBTRF; and thus, the scalar
data specified for ja, desc_a, and laf must also be
the same.
- In all cases, follow these rules:
- ib = ja
- DTYPE_A=501 or 1
- DTYPE_B=502 or 1
- NB_A = MB_B
- If DTYPE_A=1, RSRC_A=0, M_A >= k+1, and MB_A >= 1.
- If DTYPE_B=1, CSRC_B=0, N_B >= nrhs, and NB_B >= 1.
- CTXT_A = CTXT_B
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 501
| 1
| 1 × p
|
| 1
| 502
| p × 1
|
| 1
| 1
| 1 × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- A, B, af and work must have no
common elements; otherwise, results are unpredictable.
- The global positive definite symmetric band matrix A must be
stored in upper- or lower-band-packed storage mode. See the section on block
distributing a symmetric matrix in "Matrices".
Matrix A must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1, they must all specify -1.
- Although global submatrices A and B may be
block-cyclically distributed on a 1 × p or
p × 1 process grid, the values of n,
ja, ib, NB_A, and MB_B must be chosen so that each process
has at most one full or partial block of each of the global submatrices
A and B.
None
| Note: |
If the factorization performed by PDPBTRF failed because of a nonpositive
definite matrix A, the results returned by this subroutine are
unpredictable. For details, see the info output argument for PDPBTRF.
|
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- PDPBTRS was called from outside the process grid.
- The process grid is not 1 × p or
p × 1.
- uplo <> 'U' or 'L'
- n < 0
- k < 0
- k+1 > n
- ja < 1
- DTYPE_A = 1 and:
- M_A < k+1
- MB_A < 1
- RSRC_A <> 0
- The process grid is not 1 × p.
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)p-mod(ja-1,NB_A)
- uplo = 'U' and k > NB_A
- CSRC_A < 0 or CSRC_A >= p
- nrhs < 0
- ib <> ja
- ib < 1
- DTYPE_B = 1 and:
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
- The process grid is not p × 1.
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- n > (MB_B)p-mod(ib-1,MB_B)
- MB_B <> NB_A
- RSRC_B < 0 or RSRC_B >= p
- CTXT_A <> CTXT_B
If n > 0:
- ja+n-1 > N_A
- ja > N_A
- ib > M_B
- ib+n-1 > M_B
- LLD_A < k+1
- LLD_B < max(1, LOCp(M_B))
- lwork <> 0,
- lwork <> -1, and
lwork < (nrhs)(k)
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- k differs.
- nrhs differs.
- ja differs.
- DTYPE_A differs.
- DTYPE_A does not differ and:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
- DTYPE_A = 1 and:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
- ib differs.
- DTYPE_B differs.
- DTYPE_B does not differ and:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
- DTYPE_A = 1 and:
- N_B differs.
- NB_B differs.
- CSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example solves the
AX=B system, where matrix A is the same
positive definite symmetric band matrix factored in "Example" for PDPBTRF.
Notes:
- Matrix A, output from PDPBTRF, must be passed, unchanged, to
the solve subroutine PDPBTRS.
The input values for desc_a are the same values shown in "Example".
- Notice only one process grid was created, even though,
DTYPE_A = 501 and DTYPE_B = 502.
- The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, in this example,
laf is specified as 119.
- The af argument, output from PDPBTRF, must be passed, unchanged,
to the solve subroutine PDPBTRS.
- Because lwork = 0, PDPBTRS dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N K NRHS A JA DESC_A B IB DESC_B AF LAF
| | | | | | | | | | | |
CALL PDPBTRS( 'L' , 9 , 7 , 3 , A , 1 , DESC_A , B , 1 , DESC_B , AF , 119 ,
WORK LWORK INFO
| | |
WORK , 0 , INFO )
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 9
|
| MB_
| 3
|
| RSRC_
| 0
|
| LLD_B
| 3
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global matrix A stored in lower-band-packed storage mode with
block size of 3:
B,D 0 1 2
* *
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0 |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . . |
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . . |
| 1.0 1.0 1.0 | 1.0 . . | . . . |
| 1.0 1.0 1.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . .
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . .
| 1.0 1.0 1.0 | 1.0 . . | . . .
| 1.0 1.0 1.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
Global matrix B with block size of 3:
B,D 0
* *
| 8.0 36.0 44.0 |
0 | 16.0 80.0 80.0 |
| 23.0 122.0 108.0 |
| ----------------- |
| 29.0 161.0 129.0 |
1 | 34.0 196.0 144.0 |
| 38.0 226.0 154.0 |
| ----------------- |
| 41.0 250.0 160.0 |
2 | 43.0 267.0 163.0 |
| 36.0 240.0 120.0 |
* *
The following is the 1 × 3 process grid:
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|--------------------|---------------------|--------------------
| 8.0 36.0 44.0 | 29.0 161.0 129.0 | 41.0 250.0 160.0
0 | 16.0 80.0 80.0 | 34.0 196.0 144.0 | 43.0 267.0 163.0
| 23.0 122.0 108.0 | 38.0 226.0 154.0 | 36.0 240.0 120.0
Output:
Global matrix B with block size of 3:
B,D 0
* *
| 1.0 1.0 9.0 |
0 | 1.0 2.0 8.0 |
| 1.0 3.0 7.0 |
| -------------- |
| 1.0 4.0 6.0 |
1 | 1.0 5.0 5.0 |
| 1.0 6.0 4.0 |
| -------------- |
| 1.0 7.0 3.0 |
2 | 1.0 8.0 2.0 |
| 1.0 9.0 1.0 |
* *
The following is the 1 × 3 process grid:
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 9.0 | 1.0 4.0 6.0 | 1.0 7.0 3.0
0 | 1.0 2.0 8.0 | 1.0 5.0 5.0 | 1.0 8.0 2.0
| 1.0 3.0 7.0 | 1.0 6.0 4.0 | 1.0 9.0 1.0
The value of info is 0 on all processes.
PDGTSV solves the tridiagonal systems of linear equations,
AX = B, using Gaussian elimination with partial
pivoting for the general tridiagonal matrix A stored in tridiagonal
storage mode.
PDDTSV solves the tridiagonal systems of linear equations,
AX = B, using Gaussian elimination for the
diagonally dominant general tridiagonal matrix A stored in
tridiagonal storage mode.
- A represents the global square general tridiagonal submatrix
Aia:ia+n-1,
ia:ia+n-1.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
reference [51].
Table 65. Data Types
| dl, d, du, B, work
| Subroutine
|
| Long-precision real
| PDGTSV and PDDTSV
|
| Fortran
| CALL PDGTSV | PDDTSV (n, nrhs, dl, d,
du, ia, desc_a, b, ib,
desc_b, work, lwork, info)
|
| C and C++
| pdgtsv | pddtsv (n, nrhs, dl, d,
du, ia, desc_a, b, ib,
desc_b, work, lwork, info);
|
- n
- is the order of the general tridiagonal matrix A and the number
of rows in the general submatrix B, which contains the multiple
right-hand sides.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- nrhs
- is the number of right-hand sides; that is, the number of columns in
submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- dl
- is the local part of the global vector dl. This identifies the
first element of the local array DL. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array DL
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector dl contains the subdiagonal of the global
general tridiagonal submatrix A in elements ia+1 through
ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 65. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, DL is overwritten; that is, the original input is not
preserved.
- d
- is the local part of the global vector d. This identifies the
first element of the local array D. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array D
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector d contains the main diagonal of the global
general tridiagonal submatrix A in elements ia through
ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1) containing numbers of the data type
indicated in Table 65. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, D is overwritten; that is, the original input is not
preserved.
- du
- is the local part of the global vector du. This identifies the
first element of the local array DU. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array DU
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector du contains the superdiagonal of the global
general tridiagonal submatrix A in elements ia through
ia+n-2.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 65. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, DU is overwritten; that is, the original input is not
preserved.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
1 <= ia <= N_A and
ia+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid.
The following tables describe the three types of array descriptors. For
rules on using array descriptors, see "Notes and Coding Rules".
Table 66. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 67. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
|
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 68. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 69. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A = 0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 65. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B
- desc_b
- is the array descriptor for global matrix B, which may be
type-502 or type-1, as described in the following tables. For type-502 array
descriptor, the process grid is used as if it is a
p × 1 process grid. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B = 0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 65.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDGTSV and PDDTSV dynamically allocate the
work area used by the subroutine. The work area is deallocated before control
is returned to the calling program. This option is an extension to the
ScaLAPACK standard.
- If lwork = -1, PDGTSV and PDDTSV perform a work area
query and return the optimum size of work in
work1. No computation is performed and the subroutine
returns after error checking is complete.
- Otherwise, if (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- If nrhs <= 1, then:
- For PDGTSV, lwork >= 18P+MB_A+12.
- For PDDTSV, lwork >= 10P+10
- If nrhs > 1, then:
- For PDGTSV, lwork >= 24P+5(MB_A+nrhs)
- For PDDTSV, lwork >= 20P+2(MB_A)+4(nrhs)
where, in the above formulas, P is the actual number of
processes containing data.
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, you would substitute NB_A in
place of MB_A in the formulas above.
| Note: |
In ScaLAPACK 1.5, PDDTSV requires
lwork = 22P+3MB_A+4(nrhs). This value is
greater than or equal to the value required by Parallel ESSL.
|
- info
- See 'On Return'.
- dl
- is overwritten; that is, the original input is not preserved.
- d
- is overwritten; that is, the original input is not preserved.
- du
- is overwritten; that is, the original input is not preserved.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 65.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1, its
size is (at least) of length lwork.
If lwork = -1, its size is (at least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 65, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to the
optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, the factorization or the work area query
completed successfully.
| Note: |
For PDDTSV, if the input matrix A is not diagonally dominant, the
subroutine may still complete the factorization; however, results are
unpredictable.
|
If 1 <= info <= p, the portion of the
global submatrix A stored on process info-1 and
factored locally, is singular or reducible (for PDGTSV), or not diagonally
dominant (for PDDTSV). The magnitude of a pivot element was zero or too
small.
If info > p, the portion of the global
submatrix A stored on process
info-p-1 representing interactions with other
processes, is singular or reducible (for PDGTSV), or not diagonally dominant
(for PDDTSV). The magnitude of a pivot element was zero or too small.
If info > 0, the results are unpredictable.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- dl, d, du, B, and
work must have no common elements; otherwise, results are
unpredictable.
- In all cases, follow these rules:
- ia = ib
- CTXT_A = CTXT_B
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502, MB_A = MB_B.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, NB_A = MB_B.
- If DTYPE_A = 1, then:
- For a p × 1 process grid (where
p > 1), N_A = 1, NB_A>=1, and
CSRC_A = 0.
- For a 1 × p process grid, M_A = 1,
MB_A>=1, and RSRC_A = 0.
- For a 1 × 1 process grid:
- If N_A = 1, NB_A>=1, and CSRC_A = 0.
- If M_A = 1, MB_A>=1, and RSRC_A = 0.
- If DTYPE_B = 1, N_B>=nrhs, NB_B>=1, and
CSRC_B = 0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 502
| 502
| p × 1 or 1 × p
|
| 501
| 1
| p × 1
|
| 502
| 1
| p × 1
|
| 1
| 502
| 1 × p
|
| 1
| 1
| 1 × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- For PDGTSV, the global general tridiagonal matrix A must be
non-singular and irreducible. For PDDTSV, the global general tridiagonal
matrix A must be diagonally dominant to ensure numerical accuracy,
because no pivoting is performed. These subroutines use the info
argument to provide information about A, like ScaLAPACK. However,
these subroutines also issue an error message, which differs from ScaLAPACK.
- The global general tridiagonal matrix A must be stored in
tridiagonal storage mode and distributed over a one-dimensional process grid,
using block-cyclic data distribution. See the section on block-cyclically
distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrices A and B may be
block-cyclically distributed on a 1 × p or
p×1 process grid, the values of n, ia,
ib, MB_A (if (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of each of the global submatrices A and
B.
- For global tridiagonal matrix A, use of the type-1 array
descriptor with a p × 1 process grid is an extension to
ScaLAPACK 1.5. If your application needs to run with both Parallel ESSL and
ScaLAPACK 1.5, it is suggested that you use either a type-501 or a type-502
array descriptor for the matrix A.
Matrix A is a singular or reducible matrix
(for PDGTSV), or not diagonally dominant (for PDDTSV). For details, see the
description of the info argument.
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- CTXT_A <> CTXT_B
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <> 1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia-1,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
- NB_A <> MB_B
- CSRC_A <> RSRC_B
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia-1,MB_A)
- ia > M_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
- MB_A <> MB_B
- RSRC_A <> RSRC_B
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- ia <> ib
- DTYPE_B = 1 and the process grid is 1 × p
and p > 1
- nrhs < 0
- ib < 1
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- ib > M_B and (n > 0)
- ib+n-1 > M_B and
(n > 0)
- RSRC_B < 0 or RSRC_B >= p
- LLD_B < max(1,LOCp(M_B))
If DTYPE_B = 1:
- N_B < 0 and (nrhs = 0); N_B < 1
otherwise
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
In all cases:
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- nrhs differs.
- ia differs.
- ib differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
In all cases:
- DTYPE_B differs.
If DTYPE_B = 1 on all processes:
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
If DTYPE_B = 502 on all processes:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
general tridiagonal matrix A of order 12:
* *
| 2.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 |
* *
Matrix A is distributed over a 1 × 3 process grid
using block-column distribution.
Notes:
- On output, the vectors dl, d, and du are
overwritten by this subroutine.
- Notice only one process grid was created, even though,
DTYPE_A = 501 and DTYPE_B = 502.
- Because lwork = 0, this subroutine dynamically allocates
the work area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N NRHS DL D DU IA DESC_A B IB DESC_B WORK LWORK INFO
| | | | | | | | | | | | |
CALL PDGTSV( 12 , 3 , DL , D , DU , 1 , DESC_A , B , 1 , DESC_B , WORK , 0 , INFO )
-or-
N NRHS DL D DU IA DESC_A B IB DESC_B WORK LWORK INFO
| | | | | | | | | | | | |
CALL PDDTSV( 12 , 3 , DL , D , DU , 1 , DESC_A , B , 1 , DESC_B , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt1
|
| N_
| 12
|
| NB_
| 4
|
| CSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| LLD_B
| 4
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector dl with block size of 4:
B,D 0 1 2
* *
0 | . 1.0 1.0 1.0 | 1.0 1.0 1.0 1.0 | 1.0 1.0 1.0 1.0 |
* *
Global vector d with block size of 4:
B,D 0 1 2
* *
0 | 2.0 3.0 3.0 3.0 | 3.0 3.0 3.0 3.0 | 3.0 3.0 3.0 3.0 |
* *
Global vector du with block size of 4:
B,D 0 1 2
* *
0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 . |
* *
The following is the 1 × 3 process grid:
Local array DL with block size of 4:
p,q | 0 | 1 | 2
-----|----------------------|-----------------------|----------------------
0 | . 1.0 1.0 1.0 | 1.0 1.0 1.0 1.0 | 1.0 1.0 1.0 1.0
Local array D with block size of 4:
p,q | 0 | 1 | 2
-----|----------------------|-----------------------|----------------------
0 | 2.0 3.0 3.0 3.0 | 3.0 3.0 3.0 3.0 | 3.0 3.0 3.0 3.0
Local array DU with block size of 4:
p,q | 0 | 1 | 2
-----|----------------------|-----------------------|---------------------
0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 .
Global matrix B with a block size of 4:
B,D 0
* *
| 46.0 6.0 4.0 |
| 65.0 13.0 6.0 |
0 | 59.0 19.0 6.0 |
| 53.0 25.0 6.0 |
| -------------- |
| 47.0 31.0 6.0 |
| 41.0 37.0 6.0 |
1 | 35.0 43.0 6.0 |
| 29.0 49.0 6.0 |
| -------------- |
| 23.0 55.0 6.0 |
| 17.0 61.0 6.0 |
2 | 11.0 67.0 6.0 |
| 5.0 47.0 4.0 |
* *
The following is the 1 × 3 process grid:
Local matrix B with a block size of 4:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 46.0 6.0 4.0 | 47.0 31.0 6.0 | 23.0 55.0 6.0
| 65.0 13.0 6.0 | 41.0 37.0 6.0 | 17.0 61.0 6.0
0 | 59.0 19.0 6.0 | 35.0 43.0 6.0 | 11.0 67.0 6.0
| 53.0 25.0 6.0 | 29.0 49.0 6.0 | 5.0 47.0 4.0
Output:
Global matrix B with a block size of 4:
p,q | 0
-----|----------------
| 12.0 1.0 1.0
| 11.0 2.0 1.0
0 | 10.0 3.0 1.0
| 9.0 4.0 1.0
-----|----------------
| 8.0 5.0 1.0
| 7.0 6.0 1.0
1 | 6.0 7.0 1.0
| 5.0 8.0 1.0
-----|----------------
| 4.0 9.0 1.0
| 3.0 10.0 1.0
2 | 2.0 11.0 1.0
| 1.0 12.0 1.0
The following is the 1 × 3 process grid:
Local matrix B with a block size of 4:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 12.0 1.0 1.0 | 8.0 5.0 1.0 | 4.0 9.0 1.0
| 11.0 2.0 1.0 | 7.0 6.0 1.0 | 3.0 10.0 1.0
0 | 10.0 3.0 1.0 | 6.0 7.0 1.0 | 2.0 11.0 1.0
| 9.0 4.0 1.0 | 5.0 8.0 1.0 | 1.0 12.0 1.0
The value of info is 0 on all processes.
PDGTTRF factors the general tridiagonal matrix A, stored in
tridiagonal storage mode, using Gaussian elimination with partial pivoting.
PDDTTRF factors the diagonally dominant general tridiagonal matrix
A, stored in tridiagonal storage mode, using Gaussian elimination.
In these subroutine descriptions, A represents the global square
general tridiagonal submatrix
Aia:ia+n-1,
ia:ia+n-1.
To solve a tridiagonal system of linear equations with multiple right-hand
sides, follow the call to PDGTTRF or PDDTTRF with one or more calls to PDGTTRS
or PDDTTRS, respectively. The output from these factorization subroutines
should be used only as input to the solve subroutines PDGTTRS and PDDTTRS,
respectively.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See reference [51].
Table 70. Data Types
| dl, d, du, du2, af,
work
| ipiv
| Subroutine
|
| Long-precision real
| Integer
| PDGTTRF and PDDTTRF
|
| Fortran
| CALL PDGTTRF (n, dl, d, du,
du2, ia, desc_a, ipiv, af,
laf, work, lwork, info)
CALL PDDTTRF (n, dl, d, du,
ia, desc_a, af, laf, work,
lwork, info)
|
| C and C++
| pdgttrf (n, dl, d, du, du2,
ia, desc_a, ipiv, af, laf,
work, lwork, info);
pddttrf (n, dl, d, du, ia,
desc_a, af, laf, work, lwork,
info);
|
- n
- is the order of the general tridiagonal matrix A and the number
of elements in vector ipiv used in the computation.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- dl
- is the local part of the global vector dl. This identifies the
first element of the local array DL. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array DL
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector dl contains the subdiagonal of the global
general tridiagonal submatrix A in elements ia+1 through
ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, DL is overwritten; that is, the original input is not
preserved.
- d
- is the local part of the global vector d. This identifies the
first element of the local array D. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array D
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector d contains the main diagonal of the global
general tridiagonal submatrix A in elements ia through
ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1). containing numbers of the data type
indicated in Table 70. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, D is overwritten; that is, the original input is not
preserved.
- du
- is the local part of the global vector du. This identifies the
first element of the local array DU. These subroutines
compute the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array DU
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector du contains the superdiagonal of the global
general tridiagonal submatrix A in elements ia through
ia+n-2.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, DU is overwritten; that is, the original input is not
preserved.
- du2
- See 'On Return'.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501
1 <= ia <= N_A and
ia+n-1 <= N_A
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid. The following tables describe three
types of array descriptors. For rules on using array descriptors, see "Notes and Coding Rules".
Table 71. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 72. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
|
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 73. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 74. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A = 0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- ipiv
- See 'On Return'.
- af
- See 'On Return'.
- laf
- is the number of elements in array AF.
Scope: local
Specified as: a fullword integer, where:
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- For PDGTTRF, laf >= 12P+3(MB_A)
- For PDDTTRF, laf >= 12P+2(MB_A).
where, in the above formulas, P is the actual number of
processes containing data.
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, you would substitute NB_A in
place of MB_A in the formulas above.
| Note: |
In ScaLAPACK 1.5, PDDTTRF requires laf = 12P+3NB_A. This
value is greater than or equal to the value required by Parallel ESSL.
|
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 70.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDGTTRF and PDDTTRF dynamically allocate
the work area used by the subroutine. The work area is deallocated before
control is returned to the calling program. This option is an extension to the
ScaLAPACK standard.
- If lwork = -1, PDGTTRF and PDDTTRF perform a work area
query and return the optimum size of work in
work1. No computation is performed and the subroutine
returns after error checking is complete.
- Otherwise, lwork must have the following value:
For PDGTTRF, lwork >= 10P
For PDDTTRF, lwork >= 8P
where, in the above formulas, P is the actual number of
processes containing data.
- info
- See 'On Return'.
- dl
- dl is the updated local part of the global vector dl,
containing part of the factorization.
Scope: local
Returned as: a one-dimensional array of (at least)
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70.
On output, DL is overwritten; that is, the original input is not
preserved.
- d
- d is the updated local part of the global vector d,
containing part of the factorization.
Scope: local
Returned as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70.
On output, D is overwritten; that is, the original input is not
preserved.
- du
- du is the updated local part of the global vector du,
containing part of the factorization.
Scope: local
Returned as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70.
On output, DU is overwritten; that is, the original input is not
preserved.
- du2
- is the local part of the global vector du2, containing part of
the factorization.
Scope: local
Returned as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 70.
- ipiv
- is the local part of the global vector ipiv, containing the
pivot information needed by PDGTTRS. This identifies the first
element of the local array IPIV. These subroutines compute
the location of the first element of the local subarray used, based on
ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array IPIV
contains the local pieces of the leading ia+n-1 part
of the global vector.
Scope: local
Returned as: an array of (at least) length
LOCp(ia+n-1), containing fullword integers. There is
no array descriptor for ipiv. The details about the block data
distribution of global vector ipiv are stored in desc_a.
- af
- is a work area used by these subroutines and contains part of the
factorization. Its size is specified by laf.
Scope: local
Returned as: a one-dimensional array of (at least) length
laf, containing numbers of the data type indicated in Table 70.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1,
the size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of data type
indicated in Table 70, where:
- If lwork >= 1, the work1 is set to
the minimum lwork value needed.
- If lwork = -1, the work1 is set
to the optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, the factorization or work area query
completed successfully.
| Note: |
For PDDTTRF, if the input matrix A is not diagonally dominant, the
subroutine may still complete the factorization; however, results are
unpredictable.
|
If 1 <= info <= p, the portion of the
global submatrix A stored on process info-1 and
factored locally, is singular or reducible (for PDGTTRF), or not diagonally
dominant (for PDDTTRF). The magnitude of a pivot element was zero or too
small.
If info > p, the portion of the global
submatrix A stored on process
info-p-1 representing interactions with other
processes, is singular or reducible (for PDGTTRF), or not diagonally dominant
(for PDDTTRF). The magnitude of a pivot element was zero or too small.
If info > 0, the factorization is completed; however,
if you call PDGTTRS/PDDTTRS with these factors, results are
unpredictable.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- The output from these factorization subroutines should be used only as
input to the solve subroutines PDGTTRS and PDDTTRS, respectively.
The factored matrix A is stored in an internal format that
depends on the number of processes.
The scalar data specified for input argument n must be the same
for both PDGTTRF/PDDTTRF and PDGTTRS/PDDTTRS.
The global vectors for dl, d, du,
du2, and af input to PDGTTRS/PDDTTRS must be the
same as the corresponding output arguments for PDGTTRF/PDDTTRF; and
thus, the scalar data specified for ia, desc_a, and
laf must also be the same.
- In all cases, follow these rules:
- ia = ib
- If DTYPE_A=1, then:
- For a p × 1 process grid (where p>1),
N_A=1, NB_A>=1, and CSRC_A=0.
- For a 1 × p process grid (where p>1),
M_A=1, MB_A>=1, and RSRC_A=0.
- For a 1 × 1 process grid:
- If N_A=1, NB_A>=1 and CSRC_A=0.
- If M_A=1, MB_A>=1 and RSRC_A=0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| Process Grid
|
| 501
| p × 1 or 1 × p
|
| 502
| p × 1 or 1 × p
|
| 1
| p × 1 or 1 × p
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- dl, d, du, du2,
ipiv, af, and work must have no common elements;
otherwise, results are unpredictable.
- For PDGTTRF, the global general tridiagonal matrix A must be
non-singular and irreducible. For PDDTTRF, the global general tridiagonal
matrix A must be diagonally dominant to ensure numerical accuracy,
because no pivoting is performed. These subroutines use the info
argument to provide information about A, like ScaLAPACK. However,
these subroutines also issue an error message, which differs from ScaLAPACK.
- The global general tridiagonal matrix A must be stored in
tridiagonal storage mode and distributed over a one-dimensional process grid,
using block-cyclic data distribution. See the section on block-cyclically
distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrix A may be block-cyclically distributed on
a 1 × p or p × 1 process grid,
the values of n, ia, MB_A (if (the process grid is
p × 1 and DTYPE_A = 1) or
DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of global submatrix A.
- For global tridiagonal matrix A, use of the type-1 array
descriptor is an extension to ScaLAPACK 1.5. If your application needs to run
with both Parallel ESSL and ScaLAPACK 1.5, it is suggested that you use either
a type-501 or a type-502 array descriptor for the matrix A.
Matrix A is a singular or reducible matrix
(for PDGTTRF), or not diagonally dominant (for PDDTTRF). For details, see the
description of the info argument.
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <> 1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia-1,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia-1,MB_A)
- ia > M_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- laf < (minimum value) (For the minimum value, see the
laf argument description.)
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- ia differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
general tridiagonal matrix A of order 12.
* *
| 2.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 3.0 |
* *
Matrix A is stored in tridiagonal storage mode and is
distributed over a 3 × 1 process grid using block-cyclic
distribution.
Notes:
- The vectors dl, d, and du, output from
PDGTTRF, are stored in an internal format that depends on the number of
processes. These vectors are passed, unchanged, to the solve subroutine
PDGTTRS.
- The contents of the du2 and af vectors, output from
PDGTTRF, are not shown. These vectors are passed, unchanged, to the solve
subroutine PDGTTRS.
- Because lwork = 0, PDGTTRF dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N DL D DU DU2 IA DESC_A IPIV AF LAF WORK LWORK INFO
| | | | | | | | | | | | |
CALL PDGTTRF( 12 , DL , D , DU , DU2 , 1 , DESC_A , IPIV , AF , 48 , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector dl with block size of 4:
B,D 0
* *
| . |
| 1.0 |
0 | 1.0 |
| 1.0 |
| --- |
| 1.0 |
| 1.0 |
1 | 1.0 |
| 1.0 |
| --- |
| 1.0 |
| 1.0 |
2 | 1.0 |
| 1.0 |
* *
Global vector d with block size of 4:
B,D 0
* *
| 2.0 |
| 3.0 |
0 | 3.0 |
| 3.0 |
| --- |
| 3.0 |
| 3.0 |
1 | 3.0 |
| 3.0 |
| --- |
| 3.0 |
| 3.0 |
2 | 3.0 |
| 3.0 |
* *
Global vector du with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| --- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| --- |
| 2.0 |
| 2.0 |
2 | 2.0 |
| . |
* *
The following is the 3 × 1 process grid:
Local array DL with block size of 4:
p,q | 0
-----|-----
| .
| 1.0
0 | 1.0
| 1.0
-----|-----
| 1.0
| 1.0
1 | 1.0
| 1.0
-----|-----
| 1.0
| 1.0
2 | 1.0
| 1.0
Local array D with block size of 4:
p,q | 0
-----|-----
| 2.0
| 3.0
0 | 3.0
| 3.0
-----|-----
| 3.0
| 3.0
1 | 3.0
| 3.0
-----|-----
| 3.0
| 3.0
2 | 3.0
| 3.0
Local array DU with block size of 4:
p,q | 0
-----|-----
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|-----
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|-----
| 2.0
| 2.0
2 | 2.0
| .
Output:
Global vector dl with block size of 4:
B,D 0
* *
| . |
| 0.5 |
0 | 0.5 |
| 0.5 |
| ---- |
| 1.0 |
| 0.33 |
1 | 0.43 |
| 0.47 |
| ---- |
| 1.0 |
| 1.0 |
2 | 1.0 |
| 1.0 |
* *
Global vector d with block size of 4:
B,D 0
* *
| 0.5 |
| 0.5 |
0 | 0.5 |
| 2.0 |
| ---- |
| 0.33 |
| 0.43 |
1 | 0.47 |
| 2.07 |
| ---- |
| 2.07 |
| 0.47 |
2 | 0.43 |
| 0.33 |
* *
Global vector du with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| ---- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| ---- |
| 0.93 |
| 0.86 |
2 | 0.67 |
| . |
* *
Global vector ipiv with block size of 4:
B,D 0
* *
| 0 |
| 0 |
0 | 0 |
| 0 |
| - |
| 0 |
| 0 |
1 | 0 |
| 0 |
| - |
| 0 |
| 0 |
2 | 0 |
| 0 |
* *
The following is the 3 × 1 process grid:
Local array DL with block size of 4:
p,q | 0
-----|------
| .
| 0.5
0 | 0.5
| 0.5
-----|------
| 1.0
| 0.33
1 | 0.43
| 0.47
-----|------
| 1.0
| 1.0
2 | 1.0
| 1.0
Local array D with block size of 4:
p,q | 0
-----|------
| 0.5
| 0.5
0 | 0.5
| 2.0
-----|------
| 0.33
| 0.43
1 | 0.47
| 2.07
-----|------
| 2.07
| 0.47
2 | 0.43
| 0.33
Local array DU with block size of 4:
p,q | 0
-----|------
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|------
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|------
| 0.93
| 0.86
2 | 0.67
| .
Local array IPIV with block size of 4:
p,q | 0
-----|---
| 0
| 0
0 | 0
| 0
-----|---
| 0
| 0
1 | 0
| 0
-----|---
| 0
| 0
2 | 0
| 0
The value of info is 0 on all processes.
This example shows a factorization of the diagonally dominant general
tridiagonal matrix A of order 12. Matrix A is stored in
tridiagonal storage mode and distributed over a 3 × 1 process
grid using block-cyclic distribution.
Matrix A and the input and/or output values for
dl, d, du, desc_a, and info in
this example are the same as shown for "Example 1".
Notes:
- The vectors dl, d, and du, output from
PDDTTRF, are stored in an internal format that depends on the number of
processes. These vectors are passed, unchanged, to the solve subroutine
PDDTTRS.
- The contents of vector af, output from PDDTTRF, are not shown.
This vector is passed, unchanged, to the solve subroutine PDDTTRS.
- Because lwork = 0, PDDTTRF dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N DL D DU IA DESC_A AF LAF WORK LWORK INFO
| | | | | | | | | | |
CALL PDDTTRF( 12 , DL , D , DU , 1 , DESC_A , AF , 44 , WORK , 0 , INFO )
These subroutines solve the following systems of equations for multiple
right-hand sides:
- 1. AX = B
PDGTTRS solves the tridiagonal systems of linear equations, using Gaussian
elimination with partial pivoting for the general tridiagonal matrix
A stored in tridiagonal storage mode.
PDDTTRS solves the tridiagonal systems of linear equations, using Gaussian
elimination for the diagonally dominant general tridiagonal matrix
A stored in tridiagonal storage mode.
In these subroutines:
- A represents the global square general tridiagonal submatrix
Aia:ia+n-1,
ia:ia+n-1.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
These subroutines use the results of the factorization of matrix
A, produced by a preceding call to PDGTTRF or PDDTTRF,
respectively. The output from the factorization subroutines, PDGTTRF and
PDDTTRF, should be used only as input to these solve subroutines,
respectively.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
reference [51].
Table 75. Data Types
| dl, d, du, du2, B,
af, work
| ipiv
| Subroutine
|
| Long-precision real
| Integer
| PDGTTRS and PDDTTRS
|
| Fortran
| CALL PDGTTRS (transa, n, nrhs, dl,
d, du, du2, ia, desc_a,
ipiv, b, ib, desc_b, af,
laf, work, lwork, info)
CALL PDDTTRS (transa, n, nrhs, dl,
d, du, ia, desc_a, b,
ib, desc_b, af, laf, work,
lwork, info)
|
| C and C++
| pdgttrs (transa, n, nrhs, dl,
d, du, du2, ia, desc_a,
ipiv, b, ib, desc_b, af,
laf, work, lwork, info);
pddttrs (transa, n, nrhs, dl,
d, du, ia, desc_a, b,
ib, desc_b, af, laf, work,
lwork, info);
|
- transa
- indicates submatrix A is used in the computation, resulting in
solution 1.
Scope: global
Specified as: a single character;
transa = 'N'.
| Note: |
PDDTTRS does not support transa = 'C' or 'T'.
You can only migrate from the ScaLAPACK 1.5 version of this subroutine to
PDDTTRS if transa = 'N'.
|
- n
- is the order of the general tridiagonal submatrix A and the
number of rows in the general submatrix B, which contains the
multiple right-hand sides.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- nrhs
- is the number of right-hand sides; that is, the number of columns in
submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- dl
- is the local part of the global vector dl, containing part of
the factorization produced from a preceding call to PDGTTRF or PDDTTRF. This
identifies the first element of the local array DL.
These subroutines compute the location of the first element of the local
subarray used, based on ia, desc_a, and p;
therefore, the leading LOCp(ia+n-1) part of the local
array DL contains the local pieces of the leading
ia+n-1 part of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 75. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- d
- is the local part of the global vector d, containing part of
the factorization produced from a preceding call to PDGTTRF or PDDTTRF. This
identifies the first element of the local array D. These
subroutines compute the location of the first element of the local subarray
used, based on ia, desc_a, and p; therefore, the
leading LOCp(ia+n-1) part of the local array
D contains the local pieces of the leading
ia+n-1 part of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 75. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- du
- is the local part of the global vector du, containing part of
the factorization produced from a preceding call to PDGTTRF or PDDTTRF. This
identifies the first element of the local array DU.
These subroutines compute the location of the first element of the local
subarray used, based on ia, desc_a, and p;
therefore, the leading LOCp(ia+n-1) part of the local
array DU contains the local pieces of the leading
ia+n-1 part of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 75. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- du2
- is the local part of the global vector du2, containing part of
the factorization produced from a preceding call to PDGTTRF. This identifies
the first element of the local array DU2. These
subroutines compute the location of the first element of the local subarray
used, based on ia, desc_a, and p; therefore, the
leading LOCp(ia+n-1) part of the local array
DU2 contains the local pieces of the leading
ia+n-1 part of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 75. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
1 <= ia <= N_A and
ia+n-1 <= N_A
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid. The following tables describe three
types of array descriptors. For rules on using array descriptors, see "Notes and Coding Rules".
Table 76. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 77. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
|
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 78. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by these subroutines.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 79. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A = 0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by these subroutines.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- ipiv
- is the local part of the global vector ipiv, containing the
pivot indices produced on a preceding call to PDGTTRF. This identifies the
first element of the local array IPIV. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array IPIV
must contain the local pieces of the leading ia+n-1
part of the global vector.
Scope: local
Specified as: an array of (at least)
LOCp(ia+n-1), containing fullword integers. There is
no array descriptor for ipiv. The details about the block-cyclic
data distribution of global matrix A are stored in
desc_a.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 75. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For type-502 array
descriptor, the process grid is used as if it is a
p × 1 process grid. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B = 0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- is a work area used by these subroutines and contains part of the
factorization produced on a preceding call to PDGTTRF or PDDTTRF. Its size is
specified by laf.
Scope: local
Specified as: a one-dimensional array of (at least) length
laf, containing numbers of the data type indicated in Table 75.
- laf
- is the number of elements in array AF.
Scope: local
Specified as: a fullword integer, where:
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- For PDGTTRS, laf >= 12P+3(MB_A)
- For PDDTTRS, laf >= 12P+2(MB_A).
where, in the above formulas, P is the actual number of
processes containing data.
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, you would substitute NB_A in
place of MB_A in the formulas above.
| Note: |
In ScaLAPACK 1.5, PDDTTRS requires laf = 12P+3(NB_A).
This value is greater than or equal to the value required by Parallel ESSL.
|
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at
least) of length lwork.
- If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 75.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- info
- See 'On Return'.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 75.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1,
the size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of data type
indicated in Table 75, where:
- If lwork = -1, the work1 is set
to the optimum lwork value needed.
- If lwork >= 1, the work1 is set to
the minimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- indicates that a successful computation or work area query occurred.
Scope: global
Returned as: a fullword integer; info = 0.
- In your C program, argument info must be passed by reference.
- The subroutine accepts lowercase letters for the transa argument.
- The output from these factorization subroutines should be used only as
input to the solve subroutines PDGTTRS and PDDTTRS, respectively.
The factored matrix A is stored in an internal format that
depends on the number of processes.
The scalar data specified for input argument n must be the same
for both PDGTTRF/PDDTTRF and PDGTTRS/PDDTTRS.
The global vectors for dl, d, du,
du2, ipiv, and af input to
PDGTTRS/PDDTTRS must be the same as the corresponding output
arguments for PDGTTRF/PDDTTRF; and thus, the scalar data specified
for ia, desc_a, and laf must also be the same.
- In all cases, follow these rules:
- ia = ib
- CTXT_A = CTXT_B
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502, MB_A = MB_B.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, NB_A = MB_B.
- If DTYPE_A=1, then:
- For a p × 1 process grid (where p>1),
N_A=1, NB_A>=1, and CSRC_A=0.
- For a 1 × p process grid (where p>1),
M_A=1, MB_A>=1, and RSRC_A=0.
- For a 1 × 1 process grid:
- If N_A=1, NB_A>=1 and CSRC_A=0.
- If M_A=1, MB_A>=1 and RSRC_A=0.
- If DTYPE_B=1, N_B>=nrhs, NB_B>=1, and CSRC_B=0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 502
| 502
| p × 1 or 1 × p
|
| 501
| 1
| p × 1
|
| 502
| 1
| p × 1
|
| 1
| 502
| p × 1 or 1 × p
|
| 1
| 1
| p × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- dl, d, du, du2,
ipiv, af and work must have no common elements;
otherwise, results are unpredictable.
- The global general tridiagonal matrix A must be stored in
tridiagonal storage mode and distributed over a one-dimensional process grid,
using block-cyclic data distribution. See the section on block-cyclically
distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrices A and B may be
block-cyclically distributed on a 1 × p or
p × 1 process grid, the values of n,
ia, ib, MB_A (if (the process grid is
p × 1 and DTYPE_A = 1) or
DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of each of the global submatrices A and
B.
- For global tridiagonal matrix A, use of the type-1 array
descriptor is an extension to ScaLAPACK 1.5. If your application needs to run
with both Parallel ESSL and ScaLAPACK 1.5, it is suggested that you use either
a type-501 or a type-502 array descriptor for the matrix A.
None
| Note: |
If the factorization performed by PDGTTRF or PDDTTRF failed because matrix
A is singular or reducible, or is not diagonally dominant,
respectively, the results returned by this subroutine are unpredictable. For
details, see the info output argument for PDGTTRF or PDDTTRF.
|
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- CTXT_A <> CTXT_B
- transa <> 'N'
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <> 1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia-1,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
- NB_A <> MB_B
- CSRC_A <> RSRC_B
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia-1,MB_A)
- ia > MB_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
- MB_A <> MB_B
- RSRC_A <> RSRC_B
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- ia <> ib
- DTYPE_B = 1 and the process grid is 1 × p
and p > 1
- nrhs < 0
- ib < 1
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- ib > M_B and (n > 0)
- ib+n-1 > M_B and
(n > 0)
- RSRC_B < 0 or RSRC_B >= p
- LLD_B < max(1,LOCp(M_B))
If DTYPE_B = 1:
- N_B < 0 and (nrhs = 0); N_B < 1
otherwise
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
In all cases:
- laf < (minimum value) (For the minimum value, see the
laf argument description.)
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- nrhs differs.
- transa differs.
- ia differs.
- ib differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
In all cases:
- DTYPE_B differs.
If DTYPE_B = 1 on all processes:
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
If DTYPE_B = 502 on all processes:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows how to solve the system
AX=B, where matrix A is the same general
tridiagonal matrix factored in "Example 1" for PDGTTRF.
Notes:
- The vectors dl, d, and du, output from
PDGTTRF, are stored in an internal format that depends on the number of
processes. These vectors are passed, unchanged, to the solve subroutine
PDGTTRS.
- The contents of these du2 and af vectors, output from
PDGTTRF, are not shown. These vectors are passed, unchanged, to the solve
subroutine PDGTTRS.
- Because lwork = 0, PDGTTRS dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
TRANSA N NRHS DL D DU DU2 IA DESC_A IPIV B IB
| | | | | | | | | | | |
CALL PDGTTRS( N , 12 , 3 , DL , D , DU , DU2 , 1 , DESC_A , IPIV , B , 1 ,
DESC_B AF LAF WORK LWORK INFO
| | | | | |
DESC_B , AF , 48 , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| LLD_B
| 4
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector dl with block size of 4:
B,D 0
* *
| . |
| 0.5 |
0 | 0.5 |
| 0.5 |
| ---- |
| 1.0 |
| 0.33 |
1 | 0.43 |
| 0.47 |
| ---- |
| 1.0 |
| 1.0 |
2 | 1.0 |
| 1.0 |
* *
Global vector d with block size of 4:
B,D 0
* *
| 0.5 |
| 0.5 |
0 | 0.5 |
| 2.0 |
| ---- |
| 0.33 |
| 0.43 |
1 | 0.47 |
| 2.07 |
| ---- |
| 2.07 |
| 0.47 |
2 | 0.43 |
| 0.33 |
* *
Global vector du with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| ---- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| ---- |
| 0.93 |
| 0.86 |
2 | 0.67 |
| . |
* *
Global vector ipiv with block size of 4:
B,D 0
* *
| 0 |
| 0 |
0 | 0 |
| 0 |
| - |
| 0 |
| 0 |
1 | 0 |
| 0 |
| - |
| 0 |
| 0 |
2 | 0 |
| 0 |
* *
The following is the 3 × 1 process grid:
Local array DL with block size of 4:
p,q | 0
-----|------
| .
| 0.5
0 | 0.5
| 0.5
-----|------
| 1.0
| 0.33
1 | 0.43
| 0.47
-----|------
| 1.0
| 1.0
2 | 1.0
| 1.0
Local array D with block size of 4:
p,q | 0
-----|------
| 0.5
| 0.5
0 | 0.5
| 2.0
-----|------
| 0.33
| 0.43
1 | 0.47
| 2.07
-----|------
| 2.07
| 0.47
2 | 0.43
| 0.33
Local array DU with block size of 4:
p,q | 0
-----|------
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|------
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|------
| 0.93
| 0.86
2 | 0.67
| .
Local array IPIV with block size of 4:
p,q | 0
-----|---
| 0
| 0
0 | 0
| 0
-----|---
| 0
| 0
1 | 0
| 0
-----|---
| 0
| 0
2 | 0
| 0
Global matrix B with block size of 4:
B,D 0
* *
| 46.0 6.0 4.0 |
| 65.0 13.0 6.0 |
0 | 59.0 19.0 6.0 |
| 53.0 25.0 6.0 |
| -------------- |
| 47.0 31.0 6.0 |
| 41.0 37.0 6.0 |
1 | 35.0 43.0 6.0 |
| 29.0 49.0 6.0 |
| -------------- |
| 23.0 55.0 6.0 |
| 17.0 61.0 6.0 |
2 | 11.0 67.0 6.0 |
| 5.0 47.0 4.0 |
* *
The following is the 3 × 1 process grid:
Local matrix B with block size of 4:
p,q | 0
-----|----------------
| 46.0 6.0 4.0
| 65.0 13.0 6.0
0 | 59.0 19.0 6.0
| 53.0 25.0 6.0
-----|----------------
| 47.0 31.0 6.0
| 41.0 37.0 6.0
1 | 35.0 43.0 6.0
| 29.0 49.0 6.0
-----|----------------
| 23.0 55.0 6.0
| 17.0 61.0 6.0
2 | 11.0 67.0 6.0
| 5.0 47.0 4.0
Output:
Global matrix B with block size of 4:
B,D 0
* *
| 12.0 1.0 1.0 |
| 11.0 2.0 1.0 |
0 | 10.0 3.0 1.0 |
| 9.0 4.0 1.0 |
| --------------- |
| 8.0 5.0 1.0 |
| 7.0 6.0 1.0 |
1 | 6.0 7.0 1.0 |
| 5.0 8.0 1.0 |
| --------------- |
| 4.0 9.0 1.0 |
| 3.0 10.0 1.0 |
2 | 2.0 11.0 1.0 |
| 1.0 12.0 1.0 |
* *
The following is the 3 × 1 process grid:
Local matrix B with block size of 4:
p,q | 0
-----|-----------------
| 12.0 1.0 1.0
| 11.0 2.0 1.0
0 | 10.0 3.0 1.0
| 9.0 4.0 1.0
-----|-----------------
| 8.0 5.0 1.0
| 7.0 6.0 1.0
1 | 6.0 7.0 1.0
| 5.0 8.0 1.0
-----|-----------------
| 4.0 9.0 1.0
| 3.0 10.0 1.0
2 | 2.0 11.0 1.0
| 1.0 12.0 1.0
The value of info is 0 on all processes.
This example shows how to solve the system
AX=B, where matrix A is the same diagonally
dominant general tridiagonal matrix factored in "Example 2" for PDDTTRF. The input and/or output values for dl,
d, du, desc_a, and info in this example
are the same as shown for "Example 1".
Notes:
- The vectors dl, d, and du, output from
PDDTTRF, are stored in an internal format that depends on the number of
processes. These vectors are passed, unchanged, to the solve subroutine
PDDTTRS.
- The contents of vector af, output from PDDTTRF, are not shown.
This vector is passed, unchanged, to the solve subroutine PDDTTRS.
- Because lwork = 0, PDDTTRS dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
TRANSA N NRHS DL D DU IA DESC_A B IB DESC_B
| | | | | | | | | | |
CALL PDDTTRS( N , 12 , 3 , DL , D , DU , 1 , DESC_A , B , 1 , DESC_B ,
AF LAF WORK LWORK INFO
| | | | |
AF , 44 , WORK , 0 , INFO )
This subroutine solves the tridiagonal systems of linear equations,
AX = B, where the positive definite symmetric
tridiagonal matrix A is stored in parallel-symmetric-tridiagonal
storage mode. In this description:
- A represents the global positive definite symmetric tridiagonal
submatrix Aia:ia+n-1,
ia:ia+n-1.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
reference [51].
Table 80. Data Types
| d, e, B, work
| Subroutine
|
| Long-precision real
| PDPTSV
|
| Fortran
| CALL PDPTSV (n, nrhs, d, e,
ia, desc_a, b, ib, desc_b,
work, lwork, info)
|
| C and C++
| pdptsv (n, nrhs, d, e, ia,
desc_a, b, ib, desc_b, work,
lwork, info);
|
- n
- is the order of the positive definite symmetric tridiagonal matrix
A and the number of rows in the general submatrix B,
which contains the multiple right-hand sides.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- nrhs
- is the number of right-hand sides; that is, the number of columns in
submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- d
- is the local part of the global vector d. This identifies the
first element of the local array D. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array D
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector d contains the main diagonal of the global
positive definite symmetric tridiagonal submatrix A in elements
ia through ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1) containing numbers of the data type
indicated in Table 80. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, D is overwritten; that is, the original input is not
preserved.
- e
- is the local part of the global vector e. This identifies the
first element of the local array E. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array E
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector e contains the off-diagonal of the global
positive definite symmetric tridiagonal submatrix A in elements
ia through ia+n-2.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 80. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, E is overwritten; that is, the original input is not
preserved.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
1 <= ia <= N_A and
ia+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid. The following tables describe three
types of array descriptors. For rules on using array descriptors, see "Notes and Coding Rules".
Table 81. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 82. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 83. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 84. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 80. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For type-502 array
descriptor, the process grid is used as if it is a
p × 1 process grid. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)(p)-mod(ia-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(MB_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)(p)-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B = 0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(MB_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at
least) of length lwork.
- If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 80.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDPTSV dynamically allocates the work area
used by the subroutine. The work area is deallocated before control is
returned to the calling program. This option is an extension to the ScaLAPACK
standard.
- If lwork = -1, PDPTSV performs a work area query
and return the optimum size of work in work1. No
computation is performed and the subroutine returns after error checking is
complete.
- Otherwise, if (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- If nrhs <= 1, lwork >= 10P+MB_A+10.
- If nrhs > 1,
(lwork>=(20+2min(100,nrhs))P+3(MB_A)+4(nrhs)).
where, in the above formulas, P is the actual number of
processes containing data.
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, you would substitute NB_A in
place of MB_A in the formulas above.
| Note: |
In ScaLAPACK 1.5, PDPTSV requires
lwork = 22P+3MB_A+2min(100,nrhs)P+4(nrhs).
This value is greater than or equal to the value required by Parallel ESSL.
|
- info
- See 'On Return'.
- d
- is overwritten; that is, the original input is not preserved.
- e
- is overwritten; that is, the original input is not preserved.
- b
- p is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 80.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1,
the size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 80, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to
the optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite, and the factorization completed successfully or the work area query
completed successfully.
If 1 <= info <= p, the portion of
global submatrix A stored on process info-1 and
factored locally, is not positive definite. A pivot element whose value is
less than or equal to a small positive number was detected.
If info > p, the portion of global submatrix
A stored on process info-p-1
representing interactions with other processes, is not positive definite. A
pivot element whose value is less than or equal to a small positive number was
detected.
If info > 0, the results of the computation are
unpredictable.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- d, e, B, and work must have no
common elements; otherwise, results are unpredictable.
- In all cases, follow these rules:
- ia = ib
- CTXT_A = CTXT_B
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502, MB_A = MB_B.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, NB_A = MB_B.
- If DTYPE_A=1, then:
- For a p × 1 process grid (where p>1),
N_A=1, NB_A>=1, and CSRC_A=0.
- For a 1 × p process grid (where p>1),
M_A=1, MB_A>=1, and RSRC_A=0.
- For a 1 × 1 process grid:
- If N_A=1, NB_A>=1 and CSRC_A=0.
- If M_A=1, MB_A>=1 and RSRC_A=0.
- If DTYPE_B=1, N_B>=nrhs, NB_B>=1, and CSRC_B=0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 502
| 502
| p × 1 or 1 × p
|
| 501
| 1
| p × 1
|
| 502
| 1
| p × 1
|
| 1
| 502
| p × 1 or 1 × p
|
| 1
| 1
| p × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- The global symmetric tridiagonal matrix A must be positive
definite. This subroutine uses the info argument to provide
information about A, like ScaLAPACK. However, this subroutine also
issues an error message, which differs from ScaLAPACK.
- The global positive definite symmetric tridiagonal matrix A
must be stored in parallel-symmetric-tridiagonal storage mode and distributed
over a one-dimensional process grid, using block-cyclic data distribution. See
the section on block-cyclically distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrices A and B may be
block-cyclically distributed on a 1 × p or
p × 1 process grid, the values of n,
ia, ib, MB_A (if (the process grid is
p × 1 and DTYPE_A = 1) or
DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of each of the global submatrices A and
B.
- For global tridiagonal matrix A, use of the type-1 array
descriptor is an extension to ScaLAPACK 1.5. If your application needs to run
with both Parallel ESSL and ScaLAPACK 1.5, it is suggested that you use either
a type-501 or a type-502 array descriptor for the matrix A.
Matrix A is not positive definite. For
details, see the description of the info argument.
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- CTXT_A <> CTXT_B
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <>1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
- NB_A <> MB_B
- CSRC_A <> RSRC_B
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia,MB_A)
- ia > M_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
- MB_A <> MB_B
- RSRC_A <> RSRC_B
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- ia <> ib
- DTYPE_B = 1 and the process grid is 1 × p
and p > 1
- nrhs < 0
- ib < 1
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- ib > M_B and (n > 0)
- ib+n-1 > M_B and
(n > 0)
- RSRC_B <= 0 or RSRC_B >= p
- LLD_B < max(1,LOCp(M_B))
If DTYPE_B = 1:
- N_B < 0 and (nrhs = 0); N_B < 1
otherwise
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
In all cases:
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- nrhs differs.
- ia differs.
- ib differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
In all cases:
- DTYPE_B differs.
If DTYPE_B = 1 on all processes:
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
If DTYPE_B = 502 on all processes:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
positive definite symmetric tridiagonal matrix A of order 12:
* *
| 4.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 |
* *
Matrix A is stored in parallel-symmetric-tridiagonal storage
mode and is distributed over a 1 × 3 process grid using
block-cyclic distribution.
Notes:
- On output, the vectors d and e are overwritten by
this subroutine.
- Notice only one process grid was created, even though,
DTYPE_A = 501 and DTYPE_B = 502.
- Because lwork = 0, this subroutine dynamically allocates
the work area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N NRHS D E IA DESC_A B IB DESC_B WORK LWORK INFO
| | | | | | | | | | | |
CALL PDPTSV( 12 , 3 , D , E , 1 , DESC_A , B , 1 , DESC_B , WORK , 0 , INFO)
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt1
|
| N_
| 12
|
| NB_
| 4
|
| CSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| LLD_B
| 4
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector d with block size of 4:
B,D 0 1 2
* *
0 | 4.0 5.0 5.0 5.0 | 5.0 5.0 5.0 5.0 | 5.0 5.0 5.0 5.0 |
* *
Global vector e with block size of 4:
B,D 0 1 2
* *
0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 . |
* *
The following is the 1 × 3 process grid:
Local array D with block size of 4:
p,q | 0 | 1 | 2
-----|----------------------|-----------------------|----------------------
0 | 4.0 5.0 5.0 5.0 | 5.0 5.0 5.0 5.0 | 5.0 5.0 5.0 5.0
Local array E with block size of 4:
p,q | 0 | 1 | 2
-----|----------------------|-----------------------|---------------------
0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 2.0 | 2.0 2.0 2.0 .
Global matrix B with a block size of 4:
p,q | 0
-----|----------------
| 70.0 8.0 6.0
| 99.0 18.0 9.0
0 | 90.0 27.0 9.0
| 81.0 36.0 9.0
-----|----------------
| 72.0 45.0 9.0
| 63.0 54.0 9.0
1 | 54.0 63.0 9.0
| 45.0 72.0 9.0
-----|----------------
| 36.0 81.0 9.0
| 27.0 90.0 9.0
2 | 18.0 99.0 9.0
| 9.0 82.0 7.0
The following is the 1 × 3 process grid:
Local matrix B with a block size of 4:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 70.0 8.0 6.0 | 72.0 45.0 9.0 | 36.0 81.0 9.0
| 99.0 18.0 9.0 | 63.0 54.0 9.0 | 27.0 90.0 9.0
0 | 90.0 27.0 9.0 | 54.0 63.0 9.0 | 18.0 99.0 9.0
| 81.0 36.0 9.0 | 45.0 72.0 9.0 | 9.0 82.0 7.0
Output:
Global matrix B with a block size of 4:
p,q | 0
-----|----------------
| 12.0 1.0 1.0
| 11.0 2.0 1.0
0 | 10.0 3.0 1.0
| 9.0 4.0 1.0
-----|----------------
| 8.0 5.0 1.0
| 7.0 6.0 1.0
1 | 6.0 7.0 1.0
| 5.0 8.0 1.0
-----|----------------
| 4.0 9.0 1.0
| 3.0 10.0 1.0
2 | 2.0 11.0 1.0
| 1.0 12.0 1.0
The following is the 1 × 3 process grid:
Local matrix B with a block size of 4:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 12.0 1.0 1.0 | 8.0 5.0 1.0 | 4.0 9.0 1.0
| 11.0 2.0 1.0 | 7.0 6.0 1.0 | 3.0 10.0 1.0
0 | 10.0 3.0 1.0 | 6.0 7.0 1.0 | 2.0 11.0 1.0
| 9.0 4.0 1.0 | 5.0 8.0 1.0 | 1.0 12.0 1.0
The value of info is 0 on all processes.
This subroutine factors the positive definite symmetric tridiagonal matrix
A, stored in parallel-symmetric-tridiagonal storage mode, where, in
this description, A represents the global positive definite
symmetric tridiagonal submatrix
Aia:ia+n-1,
ia:ia+n-1.
To solve a tridiagonal system of linear equations with multiple right-hand
sides, follow the call to PDPTTRF with one or more calls to PDPTTRS. The
output from this factorization subroutine should be used only as input to the
solve subroutine PDPTTRS.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See reference [51].
Table 85. Data Types
| d, e, af, work
| Subroutine
|
| Long-precision real
| PDPTTRF
|
| Fortran
| CALL PDPTTRF (n, d, e, ia,
desc_a, af, laf, work, lwork,
info)
|
| C and C++
| pdpttrf (n, d, e, ia,
desc_a, af, laf, work, lwork,
info);
|
- n
- is the order of the positive definite symmetric tridiagonal matrix
A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- d
- is the local part of the global vector d. This identifies the
first element of the local array D. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array D
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector d contains the main diagonal of the global
positive definite symmetric tridiagonal submatrix A in elements
ia through ia+n-1.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1). containing numbers of the data type
indicated in Table 85. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, D is overwritten; that is, the original input is not
preserved.
- e
- is the local part of the global vector e. This identifies the
first element of the local array E. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array E
contains the local pieces of the leading ia+n-1 part
of the global vector.
The global vector e contains the off-diagonal of the global
positive definite symmetric tridiagonal submatrix A in elements
ia through ia+n-2.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 85. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
On output, E is overwritten; that is, the original input is not
preserved.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer; where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
1 <= ia <= N_A and
ia+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid. The following tables describe three
types of array descriptors.
Table 86. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 87. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
|
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 88. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 89. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A = 0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- See 'On Return'.
- laf
- is the number of elements in array AF.
Scope: local
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
laf >= 12P+3(MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
laf >= 12P+3(NB_A).
where, in the formulas above, P is the actual number of
processes containing data.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at
least) of length lwork.
- If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 85.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDPTTRF dynamically allocates the work area
used by the subroutine. The work area is deallocated before control is
returned to the calling program. This option is an extension to the ScaLAPACK
standard.
- If lwork = -1, PDPTTRF performs a work area query
and return the optimum size of work in work1. No
computation is performed and the subroutine returns after error checking is
complete.
- Otherwise, lwork >= 8P, where P is the
actual number of processes containing data.
- info
- See 'On Return'.
- d
- d is the updated local part of the global vector d,
containing part of the factorization.
Scope: local
Returned as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 85.
On output, D is overwritten; that is, the original input is not
preserved.
- e
- e is the updated local part of the global vector e,
containing part of the factorization.
Scope: local
Returned as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 85.
On output, E is overwritten; that is, the original input is not
preserved.
- af
- is a work area used by this subroutine and contains part of the
factorization. Its size is specified by laf.
Scope: local
Returned as: a one-dimensional array of (at least) length
laf, containing numbers of the data type indicated in Table 85.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1,
the size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of data type
indicated in Table 85, where:
- If lwork >= 1, the work1 is set to
the minimum lwork value needed.
- If lwork = -1, the work1 is set
to the optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite, and the factorization completed successfully or the work area query
completed successfully.
If 1 <= info <= p, the portion of
global submatrix A stored on process info-1 and
factored locally, is not positive definite. A pivot element whose value is
less than or equal to a small positive number was detected.
If info > p, the portion of global submatrix
A stored on process info-p-1
representing interactions with other processes, is not positive definite. A
pivot element whose value is less than or equal to a small positive number was
detected.
If info > 0, the factorization is completed; however,
if you call PDPTTRS with these factors, the results of the computation are
unpredictable.
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, argument info must be passed by reference.
- The output from these factorization subroutines should be used only as
input to the solve subroutine PDPTTRS.
The factored matrix A is stored in an internal format that
depends on the number of processes.
The scalar data specified for input argument n must be the same
for both PDPTTRF and PDPTTRS.
The global vectors for d, e, and af input to
PDPTTRS must be the same as the corresponding output arguments for PDPTTRF;
and thus, the scalar data specified for ia, desc_a, and
laf must also be the same.
- In all cases, follow these rules:
- If DTYPE_A=1, then:
- For a p × 1 process grid (where p>1),
N_A=1, NB_A>=1, and CSRC_A=0.
- For a 1 × p process grid (where p>1),
M_A=1, MB_A>=1, and RSRC_A=0.
- For a 1 × 1 process grid:
- If N_A=1, NB_A>=1 and CSRC_A=0.
- If M_A=1, MB_A>=1 and RSRC_A=0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| Process Grid
|
| 501
| p × 1 or 1 × p
|
| 502
| p × 1 or 1 × p
|
| 1
| p × 1 or 1 × p
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- d, e, af, and work must have no
common elements; otherwise, results are unpredictable.
- The global symmetric tridiagonal matrix A must be positive
definite. This subroutine uses the info argument to provide
information about A, like ScaLAPACK. However, this subroutine also
issues an error message, which differs from ScaLAPACK.
- The global positive definite symmetric tridiagonal matrix A
must be stored in parallel-symmetric-tridiagonal storage mode and distributed
over a one-dimensional process grid, using block-cyclic data distribution. See
the section on block-cyclically distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrix A may be block-cyclically distributed on
a 1 × p or p × 1 process grid,
the values of n, ia, MB_A (if (the process grid is
p × 1 and DTYPE_A = 1) or
DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of global submatrix A.
- For global tridiagonal matrix A, use of the type-1 array
descriptor is an extension to ScaLAPACK 1.5. If your application needs to run
with both Parallel ESSL and ScaLAPACK 1.5, it is suggested that you use either
a type-501 or a type-502 array descriptor for the matrix A.
Matrix A is not positive definite. For
details, see the description of the info argument.
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <>1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia-1,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia-1,MB_A)
- ia > M_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- laf < (minimum value) (For the minimum value, see the
laf argument description.)
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- ia differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the
positive definite symmetric tridiagonal matrix A of order 12.
* *
| 4.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 5.0 |
* *
Matrix A is stored in parallel-symmetric-tridiagonal storage
mode and is distributed over a 3 × 1 process grid using
block-cyclic distribution.
Notes:
- The vectors d and e, output from PDPTTRF, are stored
in an internal format that depends on the number of processes. These vectors
are passed, unchanged, to the solve subroutine PDPTTRS.
- The contents of the af vector, output from PDPTTRF, is not shown.
This vector is passed, unchanged, to the solve subroutine PDPTTRS.
- Because lwork = 0, this subroutine dynamically allocates
the work area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N D E IA DESC_A AF LAF WORK LWORK INFO
| | | | | | | | | |
CALL PDPTTRF( 12 , D , E , 1 , DESC_A , AF , 48 , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector d with block size of 4:
B,D 0
* *
| 4.0 |
| 5.0 |
0 | 5.0 |
| 5.0 |
| --- |
| 5.0 |
| 5.0 |
1 | 5.0 |
| 5.0 |
| --- |
| 5.0 |
| 5.0 |
2 | 5.0 |
| 5.0 |
* *
Global vector e with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| --- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| --- |
| 2.0 |
| 2.0 |
2 | 2.0 |
| . |
* *
The following is the 3 × 1 process grid:
Local array D with block size of 4:
p,q | 0
-----|-----
| 4.0
| 5.0
0 | 5.0
| 5.0
-----|-----
| 5.0
| 5.0
1 | 5.0
| 5.0
-----|-----
| 5.0
| 5.0
2 | 5.0
| 5.0
Local array E with block size of 4:
p,q | 0
-----|-----
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|-----
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|-----
| 2.0
| 2.0
2 | 2.0
| .
Output:
Global vector d with block size of 4:
B,D 0
* *
| .25 |
| .25 |
0 | .25 |
| 4.0 |
| ---- |
| .2 |
| .24 |
1 | .25 |
| 4.01 |
| ---- |
| 4.01 |
| .25 |
2 | .24 |
| .2 |
* *
Global vector e with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| ---- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| ---- |
| .49 |
| .48 |
2 | .4 |
| . |
* *
The following is the 3 × 1 process grid:
Local array D with block size of 4:
p,q | 0
-----|------
| .25
| .25
0 | .25
| 4.0
-----|------
| .2
| .24
1 | .25
| 4.01
-----|------
| 4.01
| .25
2 | .24
| .2
Local array E with block size of 4:
p,q | 0
-----|------
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|------
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|------
| .49
| .48
2 | .4
| .
The value of info is 0 on all processes.
This subroutine solves the following tridiagonal systems of linear
equations for multiple right-hand sides, using the positive definite symmetric
tridiagonal matrix A, where A is stored in
parallel-symmetric-tridiagonal storage mode:
- AX = B
In this subroutine:
- A represents the global positive definite symmetric tridiagonal
submatrix Aia:ia+n-1,
ia:ia+n-1.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
This subroutine uses the results of the factorization of matrix
A, produced by a preceding call to PDPTTRF. The output from PDPTTRF
should be used only as input to this solve subroutine.
If n = 0 or nrhs = 0, no computation is
performed and the subroutine returns after doing some parameter checking. See
reference [51].
Table 90. Data Types
| d, e, B, af, work
| Subroutine
|
| Long-precision real
| PDPTTRS
|
| Fortran
| CALL PDPTTRS (n, nrhs, d, e,
ia, desc_a, b, ib, desc_b,
af, laf, work, lwork, info)
|
| C and C++
| pdpttrs (n, nrhs, d, e, ia,
desc_a, b, ib, desc_b, af,
laf, work, lwork, info);
|
- n
- is the order of the positive definite symmetric tridiagonal submatrix
A and the number of rows in the general submatrix B,
which contains the multiple right-hand sides.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A).
where p is the number of processes in a process grid.
- nrhs
- is the number of right-hand sides; that is, the number of columns in
submatrix B used in the computation.
Scope: global
Specified as: a fullword integer; nrhs >= 0.
- d
- is the local part of the global vector d, containing part of
the factorization produced from a preceding call to PDPTTRF. This identifies
the first element of the local array D. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array D
contains the local pieces of the leading ia+n-1 part
of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 90. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- e
- is the local part of the global vector e, containing part of
the factorization produced from a preceding call to PDPTTRF. This identifies
the first element of the local array E. This subroutine
computes the location of the first element of the local subarray used, based
on ia, desc_a, and p; therefore, the leading
LOCp(ia+n-1) part of the local array E
contains the local pieces of the leading ia+n-1 part
of the global vector.
Scope: local
Specified as: a one-dimensional array of (at least) length
LOCp(ia+n-1), containing numbers of the data type
indicated in Table 90. Details about block-cyclic data distribution of global matrix A
are stored in desc_a.
- ia
- is the row or column index of the global matrix A, identifying
the first row or column of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
1 <= ia <= M_A and
ia+n-1 <= M_A.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
1 <= ia <= N_A and
ia+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A. Because vectors
are one-dimensional data structures, you may use a type-502, type-501, or
type-1 array descriptor regardless of whether the process grid is
p × 1 or 1 × p. For a type-502
array descriptor, the process grid is used as if it is a
p × 1 process grid. For a type-501 array descriptor,
the process grid is used as if it is a 1 × p process
grid. For a type-1 array descriptor, the process grid is used as if it is
either a p × 1 process grid or a
1 × p process grid. The following tables describe three
types of array descriptors. For rules on using array descriptors, see "Notes and Coding Rules".
Table 91. Type-502 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 5
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 >= RSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 92. Type-1 Array Descriptor (p × 1 Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
|
If n = 0:
M_A >= 0
Otherwise:
M_A >= 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
| N_A = 1
|
|
| 5
| MB_A
| Row block size
| MB_A >= 1 and
0 <= n <= (MB_A)(p)-mod(ia-1,MB_A)
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_A < p
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| CSRC_A = 0
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
Table 93. Type-501 Array Descriptor
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A=501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| --
| Not used by this subroutine.
| --
| --
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
Table 94. Type-1 Array Descriptor (1 × p Process Grid)
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A = 1
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)(p)-mod(ia-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A = 0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| --
| Not used by this subroutine.
| --
| --
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the first
element of the local array B. This subroutine computes the
location of the first element of the local subarray used, based on
ib, desc_b, and p; therefore, the leading
LOCp(ib+n-1) by nrhs part of the local array
B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 90. Details about the block-cyclic data distribution of global matrix
B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For type-502 array
descriptor, the process grid is used as if it is a
p × 1 process grid. For rules on using array
descriptors, see "Notes and Coding Rules".
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)(p)-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)(p)-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B = 0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1, LOCp(M_B))
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- is a work area used by this subroutine and contains part of the
factorization produced on a preceding call to PDPTTRF. Its size is specified
by laf.
Scope: local
Specified as: a one-dimensional array of (at least) length
laf, containing numbers of the data type indicated in Table 90.
- laf
- is the number of elements in array AF.
Scope: local
Specified as: a fullword integer, where:
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502,
laf >= 12P+3(MB_A).
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501,
laf >= 12P+3(NB_A).
where, in the above formulas, P is the actual number of
processes containing data.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at
least) of length lwork.
- If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 90.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, this subroutine dynamically allocates the
work area used by the subroutine. The work area is deallocated before control
is returned to the calling program. This option is an extension to the
ScaLAPACK standard.
- If lwork = -1, PDPTTRS performs a work area query
and return the optimum size of work in work1. No
computation is performed and the subroutine returns after error checking is
complete.
- Otherwise,
lwork >= (10+2min(100,nrhs))P+4(nrhs),
where P is the actual number of processes containing data.
- info
- See 'On Return'.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 90.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1,
the size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at
least) of length 1.
Scope: local
Returned as: an area of storage, containing numbers of data type
indicated in Table 90, where:
- If lwork = -1, the work1 is set to
the optimum lwork value needed.
- If lwork >= 1, the work1 is set to
the minimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- indicates that a successful computation or work area query occurred.
Scope: global
Returned as: a fullword integer; info = 0.
- In your C program, argument info must be passed by reference.
- The output from the PDPTTRF subroutine should be used only as input to the
solve subroutine PDPTTRS.
The factored matrix A is stored in an internal format that
depends on the number of processes.
The scalar data specified for input argument n must be the same
for both PDPTTRF and PDPTTRS.
The global vectors for d, e, and af input to
PDPTTRS must be the same as the corresponding output arguments for PDPTTRF;
and thus, the scalar data specified for ia, desc_a, and
laf must also be the same.
- In all cases, follow these rules:
- ia = ib
- CTXT_A = CTXT_B
- If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502, MB_A = MB_B.
- If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501, NB_A = MB_B.
- If DTYPE_A=1, then:
- For a p × 1 process grid (where p>1),
N_A=1, NB_A>=1, and CSRC_A=0.
- For a 1 × p process grid (where p>1),
M_A=1, MB_A>=1, and RSRC_A=0.
- For a 1 × 1 process grid:
- If N_A=1, NB_A>=1 and CSRC_A=0.
- If M_A=1, MB_A>=1 and RSRC_A=0.
- If DTYPE_B=1, N_B>=nrhs, NB_B>=1, and CSRC_B=0.
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 502
| 502
| p × 1 or 1 × p
|
| 501
| 1
| p × 1
|
| 502
| 1
| p × 1
|
| 1
| 502
| p × 1 or 1 × p
|
| 1
| 1
| p × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see "Determining the Number of Rows and Columns in Your Local Arrays" for descriptor type-1 or "Determining the Number of Rows or Columns in Your Local Arrays" for descriptor type-501 and type-502.
- d, e, af and work must have no
common elements; otherwise, results are unpredictable.
- The global positive definite symmetric tridiagonal matrix A
must be stored in parallel-symmetric-tridiagonal storage mode and distributed
over a one-dimensional process grid, using block-cyclic data distribution. See
the section on block-cyclically distributing a tridiagonal matrix in "Matrices".
For more information on using block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations".
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information using
block-cyclic data distribution, see "Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations". Also, see the section on distributing the right-hand side matrix in "Matrices".
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes specifies
-1 for the work area size, they must all specify -1.
- Although global matrices A and B may be
block-cyclically distributed on a 1×p or
p × 1 process grid, the values of n,
ia, ib, MB_A (if (the process grid is
p × 1 and DTYPE_A = 1) or
DTYPE_A = 502), NB_A (if (the process grid is
1 × p and DTYPE_A = 1) or
DTYPE_A = 501), must be chosen so that each process has at most one
full or partial block of each of the global submatrices A and
B.
- For global tridiagonal matrix A, use of the type-1 array
descriptor is an extension to ScaLAPACK 1.5. If your application needs to run
with both Parallel ESSL and ScaLAPACK 1.5, it is suggested that you use either
a type-501 or a type-502 array descriptor for the matrix A.
None
| Note: |
If the factorization performed by PDPTTRF failed because of a nonpositive
definite matrix A, the results returned by this subroutine are
unpredictable. For details, see the info output argument for PDPTTRF.
|
lwork = 0 and unable to allocate workspace
- DTYPE_A is invalid.
- DTYPE_B is invalid.
- CTXT_A is invalid.
- This subroutine was called from outside the process grid.
| Note: |
In the following error conditions:
- If M_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a 1 × p process grid.
- If N_A = 1 and DTYPE_A = 1, a 1 × 1 process
grid is treated as a p × 1 process grid.
|
- The process grid is not 1 × p or
p × 1.
- CTXT_A <> CTXT_B
- n < 0
- ia < 1
- DTYPE_A = 1 and M_A <>1 and N_A <> 1
If (the process grid is 1 × p and
DTYPE_A = 1) or DTYPE_A = 501:
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)(p)-mod(ia-1,NB_A)
- ia > N_A and (n > 0)
- ia+n-1 > N_A and
(n > 0)
- CSRC_A < 0 or CSRC_A >= p
- NB_A <> MB_B
- CSRC_A <> RSRC_B
If the process grid is 1 × p and
DTYPE_A = 1:
- M_A <> 1
- MB_A < 1
- RSRC_A <> 0
If (the process grid is p × 1 and
DTYPE_A = 1) or DTYPE_A = 502:
- M_A < 0 and (n = 0); M_A < 1
otherwise
- MB_A < 1
- n > (MB_A)(p)-mod(ia-1,MB_A)
- ia > M_A and (n > 0)
- ia+n-1 > M_A and
(n > 0)
- RSRC_A < 0 or RSRC_A >= p
- MB_A <> MB_B
- RSRC_A <> RSRC_B
If the process grid is p × 1 and
DTYPE_A = 1:
- N_A <> 1
- NB_A < 1
- CSRC_A <> 0
In all cases:
- ia <> ib
- DTYPE_B = 1 and the process grid is 1 × p
and p > 1
- nrhs < 0
- ib < 1
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- ib > M_B and (n > 0)
- ib+n-1 > M_B and
(n > 0)
- RSRC_B < 0 or RSRC_B >= p
- LLD_B < max(1,LOCp(M_B))
If DTYPE_B = 1:
- N_B < 0 and (nrhs = 0); N_B < 1
otherwise
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
In all cases:
- laf < (minimum value) (For the minimum value, see the
laf argument description.)
- lwork <> 0, lwork <> -1, and
lwork < (minimum value) (For the minimum value, see the
lwork argument description.)
Each of the following global input arguments are checked to determine
whether its value is the same on all processes in the process grid:
- n differs.
- nrhs differs.
- ia differs.
- ib differs.
- DTYPE_A differs.
If DTYPE_A = 1 on all processes:
- M_A differs.
- N_A differs.
- MB_A differs.
- NB_A differs.
- RSRC_A differs.
- CSRC_A differs.
If DTYPE_A = 501 on all processes:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
If DTYPE_A = 502 on all processes:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
In all cases:
- DTYPE_B differs.
If DTYPE_B = 1 on all processes:
- M_B differs.
- N_B differs.
- MB_B differs.
- NB_B differs.
- RSRC_B differs.
- CSRC_B differs.
If DTYPE_B = 502 on all processes:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows how to solve the system
AX=B, where matrix A is the same positive
definite symmetric tridiagonal matrix factored in "Example" for PDPTTRF.
Notes:
- The vectors d and e, output from PDPTTRF, are stored
in an internal format that depends on the number of processes. These vectors
are passed, unchanged, to the solve subroutine PDPTTRS.
- The contents of the af vector, output from PDPTTRF, is not shown.
This vector is passed, unchanged, to the solve subroutine PDPTTRS.
- Because lwork = 0, this subroutine dynamically allocates
the work area used by this subroutine.
ORDER = 'R'
NPROW = 3
NPCOL = 1
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
N NRHS D E IA DESC_A B IB DESC_B AF LAF WORK LWORK INFO
| | | | | | | | | | | | | |
CALL PDPTTRS( 12 , 3 , D, E , 1 , DESC_A , B , 1 , DESC_B, AF , 48 , WORK , 0 , INFO)
| Desc_A
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| Not used
| --
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt1
|
| M_
| 12
|
| MB_
| 4
|
| RSRC_
| 0
|
| LLD_B
| 4
|
| Reserved
| --
|
|
1 icontxt is the output of the BLACS_GRIDINIT call.
|
|
Global vector d with block size of 4:
B,D 0
* *
| .25 |
| .25 |
0 | .25 |
| 4.0 |
| ---- |
| .2 |
| .24 |
1 | .25 |
| 4.01 |
| ---- |
| 4.01 |
| .25 |
2 | .24 |
| .2 |
* *
Global vector e with block size of 4:
B,D 0
* *
| 2.0 |
| 2.0 |
0 | 2.0 |
| 2.0 |
| ---- |
| 2.0 |
| 2.0 |
1 | 2.0 |
| 2.0 |
| ---- |
| .49 |
| .48 |
2 | .4 |
| . |
* *
The following is the 3 × 1 process grid:
Local array D with block size of 4:
p,q | 0
-----|------
| .25
| .25
0 | .25
| 4.0
-----|------
| .2
| .24
1 | .25
| 4.01
-----|------
| 4.01
| .25
2 | .24
| .2
Local array E with block size of 4:
p,q | 0
-----|------
| 2.0
| 2.0
0 | 2.0
| 2.0
-----|------
| 2.0
| 2.0
1 | 2.0
| 2.0
-----|------
| .49
| .48
2 | .4
| .
Global matrix B with a block size of 4:
p,q | 0
-----|----------------
| 70.0 8.0 6.0
| 99.0 18.0 9.0
0 | 90.0 27.0 9.0
| 81.0 36.0 9.0
-----|----------------
| 72.0 45.0 9.0
| 63.0 54.0 9.0
1 | 54.0 63.0 9.0
| 45.0 72.0 9.0
-----|----------------
| 36.0 81.0 9.0
| 27.0 90.0 9.0
2 | 18.0 99.0 9.0
| 9.0 82.0 7.0
The following is the 3 × 1 process grid:
Local matrix B with block size of 4:
p,q | 0
-----|----------------
| 70.0 8.0 6.0
| 99.0 18.0 9.0
0 | 90.0 27.0 9.0
| 81.0 36.0 9.0
-----|----------------
| 72.0 45.0 9.0
| 63.0 54.0 9.0
1 | 54.0 63.0 9.0
| 45.0 72.0 9.0
-----|----------------
| 36.0 81.0 9.0
| 27.0 90.0 9.0
2 | 18.0 99.0 9.0
| 9.0 82.0 7.0
Output:
Global matrix B with block size of 4:
B,D 0
* *
| 12.0 1.0 1.0 |
| 11.0 2.0 1.0 |
0 | 10.0 3.0 1.0 |
| 9.0 4.0 1.0 |
| --------------- |
| 8.0 5.0 1.0 |
| 7.0 6.0 1.0 |
1 | 6.0 7.0 1.0 |
| 5.0 8.0 1.0 |
| --------------- |
| 4.0 9.0 1.0 |
| 3.0 10.0 1.0 |
2 | 2.0 11.0 1.0 |
| 1.0 12.0 1.0 |
* *
The following is the 3 × 1 process grid:
Local matrix B with block size of 4:
p,q | 0
-----|-----------------
| 12.0 1.0 1.0
| 11.0 2.0 1.0
0 | 10.0 3.0 1.0
| 9.0 4.0 1.0
-----|-----------------
| 8.0 5.0 1.0
| 7.0 6.0 1.0
1 | 6.0 7.0 1.0
| 5.0 8.0 1.0
-----|-----------------
| 4.0 9.0 1.0
| 3.0 10.0 1.0
2 | 2.0 11.0 1.0
| 1.0 12.0 1.0
The value of info is 0 on all processes.
This section contains the sparse linear algebraic equation subroutine
descriptions and their sparse utility subroutines.
This sparse utility subroutine allocates space for an array descriptor,
which is needed to establish a mapping between the global general sparse
matrix A and its corresponding distributed memory location. This
subroutine also initializes the components of the array descriptor
desc_a.
| Fortran
| CALL PADALL (n, parts, desc_a,
icontxt)
|
- n
- is the order of the global general sparse matrix A and the size
of the index space.
Scope: global
Type: required
Specified as: a fullword integer, where:
n > 0.
- parts
- is a user-supplied subroutine that specifies a mapping between a global
index for an element in the global general sparse matrix A and its
corresponding storage location on one or more processes.
Sample parts subroutines for common types of data distributions
are shown in "Sample PARTS Subroutine".
For details about how you must define the PARTS subroutine, see "Programming Considerations for the Parts Subroutine (Fortran 90 and Fortran 77)".
Scope: global
Type: required
Specified as: parts must be declared as an external
subroutine in your application program. It can be whatever name you choose.
- desc_a
- See 'On Return'.
- icontxt
- is the BLACS context parameter.
Scope: global
Type: required
Specified as: a fullword integer that was returned in a prior call to
BLACS_GRIDINIT or BLACS_GRIDMAP.
- desc_a
- is the local space allocated for the array descriptor for the global
general sparse matrix A. This subroutine also initializes the
components of the array descriptor desc_a. The components of
desc_a are updated with subsequent calls to PSPINS and finalized with
a call to PSPASB.
Table 25 describes some of the elements of MATRIX_DATA, which is one component of the
array descriptor, that you may want to reference. However, your application
programs should not modify the components of the array descriptor directly.
These components should only be updated with calls to PSPINS and PSPASB.
Type: required
Returned as: the derived data type DESC_TYPE.
- Before you call this subroutine, you must create a
np × 1 process grid, where np is the number of
processes.
- PADALL allocates desc_a as necessary. Prior to further calls to
PADALL with the same desc_a, you must call PADFREE; otherwise, there
will be a memory leak.
None
- Unable to allocate work space.
- Unable to allocate component(s) of desc_a
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- n <= 0
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- n differs.
- pv or nv, output from the user-supplied parts
subroutine, was not valid. For valid values, see the appropriate argument
description in "Programming Considerations for the Parts Subroutine (Fortran 90 and Fortran 77)".
This sparse utility subroutine allocates space for the local data of a
general sparse matrix A. It also initializes some values, which are
only for internal use, of the general sparse matrix A.
| Fortran
| CALL PSPALL (a, desc_a)
CALL PSPALL (a, desc_a, nnz)
|
- a
- See 'On Return'.
- desc_a
- is the array descriptor for a global general sparse matrix A
that is produced on a preceding call to PADALL.
Type: required
Specified as: the derived data type DESC_TYPE.
- nnz
- is an estimate of the number of non-zero elements in the local part of the
global general sparse matrix A. If the actual number of non-zero
elements is greater than nnz, Parallel ESSL attempts to allocate
additional space.
If nnz is not present, Parallel ESSL estimates how many non-zero
elements, nnz, are present based on the order of the global general
sparse matrix A.
Scope: local
Type: optional
Specified as: a fullword integer, where nnz > 0.
- a
- is the local space, which contains some internal values that are
initialized by Parallel ESSL, allocated for the global general sparse matrix
A.
Scope: local
Type: required
Returned as: the derived data type D_SPMAT.
- Before you call this subroutine, you must have called PADALL.
- For details about some of the elements stored in
DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- PSPALL allocates matrix A as necessary. Prior to further calls
to PSPALL with the same matrix A, you must call PSPFREE; otherwise,
there will be a memory leak.
None
- Unable to allocate component(s) of A.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a component(s) are not valid.
- nnz <= 0
This sparse utility subroutine allocates space for a dense vector.
| Fortran
| CALL PGEALL (x, desc_a)
|
- x
- See 'On Return'.
- desc_a
- is the array descriptor that is produced on a preceding call to PADALL.
Type: required
Specified as: the derived data type DESC_TYPE.
- x
- is a pointer to the local space of the dense vector.
Scope: local
Type: required
Returned as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- Before you call this subroutine, you must have called PADALL.
- You do not need a separate array descriptor for a dense vector because it
must conform to the size of matrix A. For details about some of the
elements stored in DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- This subroutine must be called for:
- Vector b containing the right-hand side.
- Vector x containing the initial guess to the solution.
- PGEALL allocates the dense vector as necessary. Prior to further calls to
PGEALL with the same dense vector, you must call PGEFREE; otherwise, there
will be a memory leak.
None
- Unable to allocate the dense vector.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a component(s) are not valid.
This sparse utility subroutine is used by each process to insert all blocks
of data it owns into its local part of the general sparse matrix A.
| Fortran
| CALL PSPINS (a, ia, ja, blck,
desc_a)
|
- a
- is the local part of the global general sparse matrix A that is
produced on a preceding call to PSPALL or previous call(s) to this subroutine.
Scope: local
Type: required
Specified as: the derived data type D_SPMAT.
- ia
- is the first global row index of the general sparse matrix A
that receives data from the submatrix BLCK.
Scope: local
Type: required
Specified as: a fullword integer;
1 <= ia <= DESC_A%MATRIX_DATA(M).
- ja
- is the first global column index of the general sparse matrix A
that receives data from the submatrix BLCK.
Scope: local
Type: required
Specified as: a fullword integer, where:
ja = 1.
- blck
- is the local part of the submatrix BLCK to be inserted into the
global general sparse matrix A. Each call to this subroutine
inserts one contiguous block of rows into the local part of the sparse matrix
corresponding to the global submatrix Aia:ia+BLCK%M-1,ja:ja+BLCK%N-1. This subroutine
only can insert blocks of data it owns into its local part of the general
sparse matrix A. BLCK contains the following
components:
- BLCK%M is the number of local rows in the submatrix
BLCK. Scope: local.
Specified as: a fullword integer;
1 <= BLCK%M <= DESC_A%MATRIX_DATA(N_ROW).
- BLCK%N is an upper bound on the number of local columns in the
submatrix BLCK. Scope: local.
Specified as: a fullword integer;
1 <= BLCK%N <= n, where n is the
order of the global general sparse matrix A.
- BLCK%FIDA is the storage mode for the submatrix BLCK,
where:
If BLCK%FIDA='CSR', the submatrix BLCK is stored
in the storage-by-rows storage mode. Scope: global.
Specified as: a character variable of length 5;
BLCK%FIDA='CSR'.
If BLCK%FIDA='CSR', then you must specify the
BLCK%AS, BLCK%IA1, and BLCK%IA2 components, as
follows:
- BLCK%AS is a pointer to the submatrix BLCK that is
stored by rows. See "Notes". Scope: local.
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- BLCK%IA1 is a pointer to the column numbers of each non-zero
element in the submatrix BLCK. See "Notes". Scope:
local.
Specified as: a pointer to an assumed-shape array with shape
(:), containing fullword integers;
1 <= BLCK%IA1(i) <= BLCK%N,
where:
i = 1, nz and nz is the
actual number of non-zero elements in the submatrix
BLCK.
- BLCK%IA2 is a pointer to the starting positions of each row of the
submatrix BLCK in BLCK%AS and one position past the end of
BLCK%AS. See "Notes". Scope: local.
Specified as: a pointer to an assumed-shape array with shape
(:), containing fullword integers, where:
- BLCK%IA2(1) = 1
- BLCK%IA2(BLCK%M+1) = 1+nz and
nz is the actual number of non-zero elements in the
submatrix BLCK.
Specified as: the derived data type D_SPMAT.
- desc_a
- is the descriptor vector for a global general sparse matrix A
that is produced on a preceding call to PADALL or previous call(s) to this
subroutine.
Type: required
Specified as: the derived data type DESC_TYPE.
- a
- is the updated local part of the global general sparse matrix
A, updated with data from the submatrix BLCK.
Scope: local
Type: required
Returned as: the derived data type D_SPMAT.
- desc_a
- is the updated array descriptor for the global general sparse matrix
A.
Type: required
Returned as: the derived data type DESC_TYPE.
- Before you call this subroutine, you must have called PADALL and PSPALL.
- This subroutine accepts mixed case letters for the BLCK%FIDA
component.
- Arguments BLCK and A must not have common elements;
otherwise, results are unpredictable.
- For details about some of the elements stored in
DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- The submatrix BLCK must be stored by rows; that is
BLCK%FIDA = 'CSR'. For information about the
storage-by-rows storage mode, see the ESSL Version 3 Guide and
Reference.
- Once you declare BLCK of derived data type D_SPMAT, you must allocate the
components of BLCK that point to an array. The following example shows how to
code the allocate statement if each row of the submatrix BLCK
contains no more than 20 elements:
TYPE(D_SPMAT) :: BLCK !Declare the BLCK variable
.
.
.
ALLOCATE(BLCK%AS(20),BLCK%IA1(20),BLCK%IA2(2)) !Allocate array pointers
When you are finished calling PSPINS, you should deallocate
BLCK%AS, BLCK%IA1, and BLCK%IA2.
- Each process has to call PSPINS as many times as necessary to insert the
local rows it owns. It is also possible to call PSPINS multiple times to
insert different or duplicate coefficients of the same local row it owns. For
information on how duplicate coefficients are handled, see the
dupflag argument description in PSPASB. For an example of inserting
coefficients of the same local row, see "Example".
None
- Unable to allocate work space.
- Unable to allocate component(s) of A.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- ia < 1 or
ia > DESC_A%MATRIX_DATA(M)
- ja <> 1
- desc_a component(s) are not valid.
- The sparse matrix A is not valid.
- BLCK%M < 1 or
BLCK%M > DESC_A%MATRIX_DATA(N_ROW)
- BLCK%N < 1 or BLCK%N > n
- BLCK%FIDA <> 'CSR'
- One or more rows to be inserted into submatrix A does not
belong to the process.
This piece of an example shows how to insert coefficients
into the same GLOB_ROW row by calling PSPINS multiple times. It would be
useful in finite element applications, where PSPINS inserts one element at a
time into the global matrix, but more than one element may contribute to the
same matrix row. In this case, PSPINS is called with the same value of
ia by all the elements contributing to that row.
For a complete example, see Example--Using the Fortran 90 Sparse Subroutines.
.
.
.
DO GLOB_ROW = 1, N
ROW_MAT%DESCRA(1) = 'G'
ROW_MAT%FIDA = 'CSR'
ROW_MAT%IA2(1) = 1
ROW_MAT%IA2(2) = 1
IA = GLOB_ROW
! (x-1,y,z)
ROW_MAT%AS(1) = COEFF(X-1,Y,Z,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X-1,Y,Z)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x,y-1,z)
ROW_MAT%AS(1) = COEFF(X,Y-1,Z,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X,Y-1,Z)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x,y,z-1)
ROW_MAT%AS(1) = COEFF(X,Y,Z-1,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X,Y,Z-1)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x,y,z)
ROW_MAT%AS(1) = COEFF(X,Y,Z,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X,Y,Z)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x,y,z+1)
ROW_MAT%AS(1) = COEFF(X,Y,Z+1,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X,Y,Z+1)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x,y+1,z)
ROW_MAT%AS(1) = COEFF(X,Y+1,Z,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X,Y+1,Z)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
! (x+1,y,z)
ROW_MAT%AS(1) = COEFF(X+1,Y,Z,X,Y,Z)
ROW_MAT%IA1(1) = IDX(X+1,Y,Z)
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
END DO
.
.
.
This sparse utility subroutine is used by each process to insert all blocks
of data it owns into its local part of the dense vector.
| Fortran
| CALL PGEINS (x, blck, desc_a, ix)
|
- x
- is a pointer to the local space for the dense vector that is produced by a
preceding call to PGEALL or previous call(s) to this subroutine.
Scope: local
Type: required
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- blck
- is the local part of the submatrix BLCK to be inserted into the
dense vector. Each call to this subroutine inserts one contiguous block of
data into the local part of the dense vector corresponding to the global
submatrix
Xix:ix+size(blck,1)-1.
This subroutine only inserts a block of data it owns into its local part of
the dense vector.
Scope: local
Type: required
Specified as: an assumed-shape array with shape (:), containing
long-precision real numbers, where:
1 <= size(blck,1) <= DESC_A%MATRIX_DATA(N_ROW)
- desc_a
- is the array descriptor that is produced by a preceding call to PADALL or
PSPINS.
Type: required
Specified as: the derived data type DESC_TYPE.
- ix
- is the first global row index of the dense vector that receives data from
the submatrix BLCK.
Scope: local
Type: optional
Specified as: a fullword integer;
1 <= ix <= DESC_A%MATRIX_DATA(M). The
default value is 1.
- x
- is a pointer to the local space for the dense vector, updated with local
data from the submatrix BLCK.
Scope: local
Type: required
Returned as: a pointer to an assumed-sized array with shape
(:), containing long-precision real numbers.
- Before you call this subroutine, you must have called PGEALL and PADALL.
- You do not need a separate array descriptor for a dense vector because it
must conform to the size of matrix A. For details about some of the
elements stored in DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- This subroutine must be called for:
- Vector b containing the right-hand side.
- Vector x containing the initial guess to the solution.
- Each process has to call PGEINS as many times as necessary to insert the
local elements it owns. It is also possible to call PGEINS multiple times to
insert different coefficients of the same local row it owns. Duplicate
coefficients are overwritten.
None
None.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- desc_a component(s) are not valid.
- The process grid is not np × 1.
- ix < 1 or
ix > DESC_A%MATRIX_DATA(M)
- size(x,1) < max(1,DESC_A%MATRIX_DATA(N_ROW))
- size(blck,1) < 1 or
size(blck,1) > DESC_A%MATRIX_DATA(N_ROW)
- One or more elements to be inserted into the dense vector does not belong
to the process.
This sparse utility subroutine uses the output from PSPINS to assemble the
global general sparse matrix A and its array descriptor
desc_a.
| Fortran
| CALL PSPASB (a, desc_a)
CALL PSPASB (a, desc_a, mtype, stor,
dupflag, info)
|
- a
- is the local part of the global general sparse matrix A that is
produced by previous call(s) to PSPINS.
Scope: local
Type: required
Specified as: the derived data type D_SPMAT.
- desc_a
- is the array descriptor for the global general sparse matrix A
that is produced by previous call(s) to PSPINS.
Type: required
Specified as: the derived data type DESC_TYPE.
- mtype
- indicates the form of the global sparse matrix A used,
where:
If mtype = 'GEN', A is a general sparse
matrix.
Scope: global
Type: optional
Specified as: a character variable of length 5;
mtype = 'GEN'. The default value is 'GEN'.
- stor
- indicates the storage mode that the global general sparse matrix
A is returned in, where:
If stor = 'DEF', this subroutine chooses an
appropriate storage mode, which is an internal format accepted by the
preconditioner and solver subroutines, for storing the global general sparse
matrix A on output.
If stor = 'CSR', the global general sparse matrix
A is stored in the storage-by-rows storage mode on output.
Scope: global
Type: optional
Specified as: a character variable of length 5;
stor = 'DEF' or 'CSR'. The default value is
'DEF'.
- dupflag
- is a flag indicating how to use coefficients that are specified more than
once on the same process; that is, duplicate coefficients within the same
local part of the matrix A:
If dupflag = 0, this subroutine uses the first of the
duplicate coefficients.
If dupflag = 1, this subroutine adds all the duplicate
coefficients with the same indices.
If dupflag = 2, this subroutine raises an error condition
indicating that there are unexpected duplicate coefficients.
Scope: global
Type: optional
Specified as: a fullword integer; dupflag = 0, 1, or
2. The default value is 0.
- info
- See 'On Return'.
- a
- is the updated local part of the global general sparse matrix
A, where:
If stor = 'DEF', this subroutine chooses an
appropriate storage mode, which is an internal format accepted by the
preconditioner and solver subroutines, for storing the global general sparse
matrix A on output.
If stor = 'CSR', the global general sparse matrix
A is stored in the storage-by-rows storage mode on output.
Scope: local
Type: required
Returned as: the derived data type D_SPMAT.
- desc_a
- is the final updated array descriptor for the global general sparse matrix
A.
Type: required
Returned as: the derived data type DESC_TYPE.
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, then one or more of the following
computational errors occurred and the appropriate error messages were issued,
indicating an error exit, where:
- If info = 1, the sparse matrix A contains
duplicate coefficients.
- If info = 2, the sparse matrix A contains
empty row(s).
Scope: global
Type: optional
Returned as: a fullword integer; info >= 0.
- Before you call this subroutine, you must have called PSPINS as many times
as needed; that is, you must have completed building the matrix with call(s)
to PSPINS before you place a call to this subroutine.
- This subroutine accepts mixed case letters for the mtype and
stor arguments.
- For details about some of the elements stored in
DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
The sparse matrix A contains duplicate
coefficients or empty row(s). For details, see the description of the
info argument.
- Unable to allocate work space.
- Unable to allocate component(s) of desc_a.
- Unable to allocate component(s) of A.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- desc_a component(s) are not valid.
- The process grid is not np × 1.
- The sparse matrix A is not valid.
- mtype <> 'GEN'
- stor <> 'DEF' or 'CSR'
- dupflag <> 0, 1, or 2
- Some local rows in the sparse matrix A are missing.
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- mtype differs.
- stor differs.
- dupflag differs.
This sparse utility subroutine assembles a dense vector.
| Fortran
| CALL PGEASB (x, desc_a)
|
- x
- is a pointer to the local part of the dense vector that is produced by
previous call(s) to PGEINS.
Scope: local
Type: required
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- desc_a
- is the array descriptor, which was finalized in a preceding call to
PSPASB.
Type: required
Specified as: the derived data type DESC_TYPE.
- x
- is a pointer to the local part of the global dense vector.
Scope: local
Type: required
Returned as: a pointer to an assumed-sized array with shape
(:), containing long-precision real numbers.
- Before you call this subroutine, you must have called PGEINS as many times
as needed; that is, you must have completed building the dense vectors with
call(s) to PGEINS before you place a call to this subroutine.
Before you call this subroutine, you must have called PSPASB.
- You do not need a separate array descriptor for a dense vector because it
must conform to the size of matrix A. For details about some of the
elements stored in DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- This subroutine must be called for:
- Vector b containing the right-hand side.
- Vector x containing the initial guess to the solution.
None
None.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a component(s) are not valid.
- size(x,1) < DESC_A%MATRIX_DATA(N_ROW)
This subroutine computes a preconditioner for a global general sparse
matrix A that should be passed unchanged to the PSPGIS subroutine.
The preconditioners include diagonal scaling or an incomplete LU
factorization.
| Fortran
| CALL PSPGPR (iprec, a, prcs, desc_a)
CALL PSPGPR (iprec, a, prcs, desc_a,
info)
|
- iprec
- is a flag that determines the type of preconditioning, where:
If iprec = 0, which is referred to as none,
indicates the local part of the submatrix A is not preconditioned.
PSPGIS will not be effective in this case, unless the coefficient matrix is
well conditioned; if your input matrix is not well conditioned, you should
consider using iprec = 1 or 2.
If iprec = 1, which is referred to as diagsc,
indicates the local part of the submatrix A is preconditioned by a
local diagonal submatrix.
If iprec = 2, which is referred to as ilu,
indicates the local part of the submatrix A is preconditioned by a
local incomplete LU factorization.
It is suggested that you use a preconditioner. For an explanation, see "Notes and Coding Rules".
Scope: global
Type: required
Specified as: a fullword integer, where:
iprec = 0, 1, or 2.
- a
- is the local part of the global general sparse matrix A,
finalized on a preceding call to PSPASB.
Scope: local
Type: required
Specified as: the derived data type D_SPMAT.
- prcs
- See 'On Return'.
- desc_a
- is the array descriptor for the global general sparse matrix A
that was finalized in a call to PSPASB.
Type: required
Specified as: the derived data type DESC_TYPE.
- info
- See 'On Return'.
- prcs
- is the preconditioner data structure prcs that must be passed
unchanged to PSPGIS.
Scope: local
Type: required
Returned as: the derived data type D_PRECN.
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, the value stored in info
indicates the row index in the global general sparse matrix A where
the preconditioner failed.
Scope: global
Type: optional
Returned as: a fullword integer; info >= 0.
- Before you call this subroutine, you must have called PSPASB and PGEASB.
- PSPGPR allocates prcs, as necessary. Prior to further calls to
PSPGPR with the same prcs, you must call PSPFREE; otherwise, there
will be a memory leak.
- For details about some of the elements stored in
DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- Parallel ESSL builds the preconditioner, prcs, which is specified
as derived data type D_PRECN, and its components. All the components of
derived data type D_PRECN are used for internal use only.
- The convergence rate of an iterative method as applied to a given system
of linear equations depends on the spectral properties of the coefficient
matrix of the linear system; therefore it is often convenient to apply a
linear transformation to the system such that the solution of the transformed
system is the same (in exact arithmetic) as that of the original, but the
spectral properties and the convergence behavior are more favorable. Such a
transformation is called preconditioning. If a matrix M
approximates A, then:
(M-1)Ax =
(M-1)b
is a preconditioned system and M is called a preconditioner. In
practice, the new coefficient matrix (M-1)A
is almost never formed explicitly, but rather its action is computed during
the application of the iterative method. The effectiveness of the
preconditioning operation depends on a trade-off between how well M
approximates A and how costly it is to compute and invert it; no
single preconditioner will give best overall performance under all situations.
Note finally that it is quite rare for a linear system to behave well enough
so as not to require preconditioning; indeed most linear systems originating
from the discretization of difficult physical problems require preconditioning
to have any convergence at all.
See references [9] and [37].
- The preconditioner for the sparse matrix A is unstable. For
details, see the info output argument for this subroutine.
- Unable to allocate work space.
- Unable to allocate component(s) of prcs.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a component(s) are not valid.
- iprec <> 0, 1, or 2
- The storage format for A is not supported.
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- iprec differs.
This subroutine solves a general sparse linear system of equations, using
an iterative algorithm, with or without preconditioning. The methods include
the more smoothly converging variant of the CGS method (Bi-CGSTAB), conjugate
gradient squared (CGS), or transpose-free quasi-minimal residual method
(TFQMR).
See references [7], [9], [12], and [35].
| Fortran
| CALL PSPGIS (a, b, x, prcs,
desc_a)
CALL PSPGIS (a, b, x, prcs,
desc_a, iparm, rparm, info)
|
- a
- is the local part of the coefficient matrix A, produced on a
previous call to PSPASB.
Scope: local
Type: required
Specified as: the derived data type D_SPMAT.
- b
- is a pointer to the local part of the global vector b,
containing the right-hand side of the matrix problem and produced on a
previous call to PGEASB.
Scope: local
Type: required
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- x
- is a pointer to the local part of the global vector x,
containing the initial guess to the solution of the linear system and produced
on a previous call to PGEASB.
Scope: local
Type: required
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- prcs
- is the preconditioner data structure prcs, produced on a
previous call to PSPGPR.
Scope: local
Type: required
Specified as: the derived data type D_PRECN.
- desc_a
- is the array descriptor, produced on a previous call to PSPASB, for the
global general sparse matrix A.
Type: required
Specified as: the derived data type DESC_TYPE.
- iparm
- is an array of parameters, IPARM(i), where:
- IPARM(1) is the flag, referred to as methd, used to
select the iterative procedure used, where:
If methd = 1, the more smoothly converging variant of the
CGS method, referred to as Bi-CGSTAB, is used.
If methd = 2, the conjugate gradient squared method,
referred to as CGS, is used.
If methd = 3, the transpose-free quasi-minimal residual
method, referred to as TFQMR, is used.
- IPARM(2) is the flag, istopc, used to select the
stopping criterion used in the computation, where the following items are used
in the definitions of the stopping criteria below:
- epsilon is the desired relative accuracy and is stored in eps
- xj is the solution found at the j-th
iteration.
- rj and r0 are the
preconditioned residuals obtained at iterations j and 0,
respectively. (The residual at iteration j is defined as
b-Axj.)
If istopc = 1, the iterative method is stopped when:
||rj||2 /
||xj||2 < epsilon
If istopc = 2, the iterative method is stopped
when:
||rj||2 /
||r0||2 < epsilon
If istopc = 3, the iterative method is stopped when:
||xj
-xj-1||2 /
||xj||2 < epsilon
| Note: |
Stopping criterion 3 performs poorly with the TFQMR method; therefore, if you
specify TFQMR (methd = 3), you should not specify stopping
criterion 3.
|
- IPARM(3) is the maximum number of iterations itmax
allowed.
- IPARM(4), referred to as itrace, has the following
meaning:
If itrace = 0, then itrace is ignored.
If itrace > 0, an informational message about the
convergence, which is based on the stopping criterion described in
istopc, is issued at every itrace-th iteration and upon
exit.
- IPARM(5), see 'On Return'.
- IPARM(6) through IPARM(20) are reserved.
Scope: global
Type: optional
Default:
- methd = 1
- istopc = 1
- itmax = 500
- itrace = 0
Specified as: an array of length 20, containing fullword integers,
where:
- methd = 1, 2, or 3
- istopc = 1, 2, or 3
- itmax >= 0
- itrace >= 0
- IPARM(6) through IPARM(20) should be set to zero.
- rparm
- is an array of parameters, RPARM(i), where:
- RPARM(1), referred to as eps, is the relative accuracy
epsilon used in the stopping criterion.
- RPARM(2), see 'On Return'.
- RPARM(3) through RPARM(20) are reserved.
Scope: global
Type: optional
Default: eps = 10-8
Specified as: an array of length 20, containing long-precision real
numbers, where:
- eps >= 0.
- RPARM(3) through RPARM(20) should be set to zero.
- info
- See 'On Return'.
- x
- is a pointer to the local part of the solution vector x
Scope: local
Type: required
Returned as: a pointer to an assumed-shape array of shape (:),
containing long-precision real numbers.
- iparm
- has the following meaning, when iparm is
present:
IPARM(5) is the number of iterations, iter, performed
by this subroutine.
Scope: global
Type: optional
Returned as: an array of length 20, containing fullword integers,
where iter >= 0.
- rparm
- has the following meaning, when rparm is
present:
RPARM(2) contains the estimate of the error, err, of
the solution, according to the stopping criterion, istopc, in use.
For details, see the istopc argument description.
Scope: global
Type: optional
Returned as: an array of length 20, containing long-precision real
numbers, where err >= 0.
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, then this subroutine exceeded
itmax iterations without converging. You may want to try the
following to get your matrix to converge:
- You can increase the number of iterations and call this subroutine again
without making any other changes to your program.
- You can change the requested precision and/or the stopping
criterion; your original precision requirement may be too stringent under a
given stopping criterion.
- You can use a preconditioner if you were not already doing so, or to
change the one you were using. Note also that the efficiency of the
preconditioner may depend on the data distribution strategy adopted. See "Notes and Coding Rules".
Scope: global
Type: optional
Returned as: a fullword integer; info >= 0.
- Before you call this subroutine, you must have called PSPGPR.
- For details about some of the elements stored in
DESC_A%MATRIX_DATA, see "Derived Data Type DESC_TYPE".
- Parallel ESSL builds the preconditioner, prcs, which is specified
as derived data type D_PRECN, and its components. All the components of
derived data type D_PRECN are used for internal use only.
This subroutine exceeded itmax iterations
without converging. Vector x contains the approximate solution
computed at the last iteration.
| Note: |
If the preconditioner computed by PSPGPR failed because the sparse matrix
A is unstable, the results returned by this subroutine are
unpredictable. For details, see the info output argument for PSPGPR.
|
You may want to try the following to get your matrix to converge:
- You can increase the number of iterations and call this subroutine again
without making any other changes to your program.
- You can change the requested precision and/or the stopping
criterion; your original precision requirement may be too stringent under a
given stopping criterion.
- You can use a preconditioner if you were not already doing so, or to
change the one you were using. Note also that the efficiency of the
preconditioner may depend on the data distribution strategy adopted. See "Notes and Coding Rules".
- Unable to allocate work space.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a component(s) are not valid.
- The sparse matrix A is not valid.
- size(iparm) < 20
- size(rparm) < 20
- eps < 0.0
- methd <> 1, 2, or 3
- iprec <> 0, 1, or 2
- istopc <> 1, 2, or 3
- itmax < 0
- itrace < 0
- The storage format for the sparse matrix A is not supported.
- size(x) < DESC_A%MATRIX_DATA(N_ROW)
- size(b) < DESC_A%MATRIX_DATA(N_ROW)
- The preconditioner data structure prcs is not valid.
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- eps differs.
- methd differs.
- istopc differs.
- itmax differs.
- itrace differs.
- Component(s) of prcs differ.
This sparse utility subroutine deallocates space that is used for a dense
vector.
| Fortran
| CALL PGEFREE (x, desc_a)
|
- x
- is a pointer to the dense vector x.
Scope: local
Type: required
Specified as: a pointer to an assumed-shape array with shape
(:), containing long-precision real numbers.
- desc_a
- is the array descriptor for the sparse matrix A.
Type: required
Specified as: the derived data type DESC_TYPE.
- Before you call this subroutine, you must have called PGEALL.
- You must deallocate b, x, sparse matrix
A, and preconditioner data structure prcs before you
deallocate the array descriptor desc_a.
None
None.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- The pointer x is not associated and therefore cannot be
deallocated.
This sparse utility subroutine deallocates space that is used for a global
general sparse matrix A or a preconditioner data structure
prcs.
| Fortran
| CALL PSPFREE (a, desc_a)
CALL PSPFREE (prcs, desc_a)
|
- a
- is the general sparse matrix A.
Scope: local
Type: required
Specified as: the derived data type D_SPMAT.
- prcs
- is the preconditioner data structure prcs.
Scope: local
Type: required
Specified as: the derived data type D_PRECN.
- desc_a
- is the array descriptor for the sparse matrix A.
Type: required
Specified as: the derived data type DESC_TYPE.
- Before you call this subroutine to deallocate the sparse matrix
A, you must have called PSPALL.
Before you call this subroutine to deallocate the preconditioner data
structure prcs, you must have called PSPGPR.
- You must deallocate b, x, sparse matrix
A, and preconditioner data structure prcs before you
deallocate the array descriptor desc_a.
- PSPGPR allocates components of prcs as necessary. Prior to
further calls to PSPGPR with the same prcs you must call PSPFREE;
otherwise, there will be a memory leak.
- PSPALL allocates matrix A as necessary. Prior to further calls
to PSPALL with the same matrix A, you must call PSPFREE; otherwise,
there will be a memory leak.
None
None.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- The preconditioner data structure prcs is not valid.
- The pointer components of A or prcs are not associated
and therefore cannot be deallocated.
This sparse utility subroutine deallocates space that is used for the array
descriptor for a global general sparse matrix A.
| Fortran
| CALL PADFREE (desc_a)
|
- desc_a
- is the array descriptor for the sparse matrix A.
Type: required
Specified as: the derived data type DESC_TYPE.
- Before you call this subroutine, you must have called PADALL.
- You must deallocate b, x, sparse matrix
A, and preconditioner data structure prcs before you
deallocate the array descriptor desc_a.
- PADALL allocates desc_a as necessary. Prior to further calls to
PADALL with the same desc_a, you must call PADFREE; otherwise, there
will be a memory leak.
None
None.
- desc_a has not been initialized.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
This example finds the solution to the linear system
Ax = b. It also contains an application program
that shows how you can use the Fortran 90 sparse linear algebraic equation
subroutines and their utilities to solve this example.
The following is the general sparse matrix A:
* *
| 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 0.0 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 |
* *
The following is the dense vector b, containing the right-hand
side:
* *
| 2.0 |
| 1.0 |
| 3.0 |
| 2.0 |
| 2.0 |
| 2.0 |
| 2.0 |
| 2.0 |
| 3.0 |
* *
The following is the dense vector x, containing the initial
guess to the solution:
* *
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
| 0.0 |
* *
Global vector x:
B,D 0
* *
| 1.0 |
0 | 1.0 |
| 1.0 |
| --- |
| 1.0 |
1 | 1.0 |
| 1.0 |
| --- |
| 1.0 |
2 | 1.0 |
| 1.0 |
* *
The following is the 3 × 1 process grid:
Local vector x:
p,q | 0
------|------
| 1.0
0 | 1.0
| 1.0
------|------
| 1.0
1 | 1.0
| 1.0
------|------
| 1.0
2 | 1.0
| 1.0
ITER = 4
ERR = 0.4071D-15
The value of info is 0 on all processes.
This application program illustrates how to use the Fortran 90 sparse
linear algebraic equation subroutines and their utilities.
@process init(f90ptr)
!
! This program illustrates how to use the PESSL F90 Sparse Iterative
! Solver and its supporting utility subroutines. A very simple problem
! (DSRIS Example 1 from the ESSL Guide and Reference) using an
! HPF BLOCK data distribution is solved.
!
PROGRAM EXAMPLE90
! Interface module required to use the PESSL F90 Sparse Iterative Solver
USE F90SPARSE
IMPLICIT NONE
! Interface definition for the PARTS subroutine PART_BLOCK
INTERFACE PART_BLOCK
SUBROUTINE PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
END SUBROUTINE PART_BLOCK
END INTERFACE
! Parameters
CHARACTER, PARAMETER :: ORDER='R'
INTEGER, PARAMETER :: IZERO=0, IONE=1
! Sparse Matrices
TYPE(D_SPMAT) :: A, BLCK
! Preconditioner Data Structure
TYPE(D_PRECN) :: PRC
! Dense Vectors
REAL(KIND(1.D0)), POINTER :: B(:), X(:)
! Communications data structure
TYPE(DESC_TYPE) :: DESC_A
! BLACS parameters
INTEGER :: NPROW, NPCOL, ICTXT, IAM, NP, MYROW, MYCOL
! Solver parameters
INTEGER :: ITER, ITMAX, IERR, ITRACE,
& IPREC, METHD, ISTOPC, IPARM(20)
REAL(KIND(1.D0)) :: ERR, EPS, RPARM(20)
! Other variables
CHARACTER*5 :: AFMT, ATYPE
INTEGER :: IRCODE, IRCODE1, IRCODE2, IRCODE3
INTEGER :: I,J
INTEGER :: N,NNZERO
INTEGER, POINTER :: PV(:)
INTEGER :: LPROCS, NROW, NCOL
INTEGER :: GLOBAL_INDX, NV_COUNT
INTEGER :: GLOBAL_INDX_OWNER, NV
INTEGER :: LOCAL_INDX
!
! Global Problem
! DSRIS Example 1 from the ESSL Guide and Reference
!
REAL*8 :: A_GLOBAL(22),B_GLOBAL(9),XINIT_GLOBAL(9)
INTEGER :: JA(22),IA(10)
DATA A_GLOBAL /2.D0,2.D0,-1.D0,1.D0,2.D0,1.D0,2.D0,-1.D0,
$ 1.D0,2.D0,-1.D0,1.D0,2.D0,-1.D0,1.D0,2.D0,
$ -1.D0,1.D0,2.D0,-1.D0,1.D0,2.D0/
DATA JA /1,2,3,2,3,1,4,5,4,5,6,5,6,7,6,7,8,
$ 7,8,9,8,9/
DATA IA /1,2,4,6,9,12,15,18,21,23/
DATA B_GLOBAL /2.D0,1.D0,3.D0,2.D0,2.D0,2.D0,2.D0,2.D0,
$ 3.D0/
DATA XINIT_GLOBAL /0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,
$ 0.D0/
! Initialize BLACS
! Define a NP x 1 Process Grid
CALL BLACS_PINFO(IAM, NP)
CALL BLACS_GET(IZERO, IZERO, ICTXT)
CALL BLACS_GRIDINIT(ICTXT, ORDER, NP, IONE)
CALL BLACS_GRIDINFO(ICTXT, NPROW, NPCOL, MYROW, MYCOL)
!
! Initialize the global problem size
!
N = SIZE(IA)-1
!
! Guess for the local number of nonzeros
!
NNZERO = SIZE(A_GLOBAL)
!
! Allocate and initialize some elements of the sparse matrix A
! its descriptor vector, DESC_A, the rhs vector B, and the
! solution vector X.
!
CALL PADALL(N,PART_BLOCK,DESC_A,ICTXT)
CALL PSPALL(A,DESC_A,NNZ=NNZERO)
CALL PGEALL(B,DESC_A)
CALL PGEALL(X,DESC_A)
!
! Allocate an integer work area to be used as an argument for
! the PART_BLOCK PARTS subroutine
!
NROW = N
NCOL = NROW
LPROCS = MAX(NPROW, NROW + NCOL)
ALLOCATE(PV(LPROCS), STAT = IRCODE)
IF (IRCODE /= 0) THEN
WRITE(6,*) 'PV Allocation failed'
CALL BLACS_ABORT(ICTXT,-1)
STOP
ENDIF
! SETUP BLCK
BLCK%M = 1
BLCK%N = NCOL
BLCK%FIDA = 'CSR'
ALLOCATE(BLCK%AS(BLCK%N),STAT=IRCODE1)
ALLOCATE(BLCK%IA1(BLCK%N),STAT=IRCODE2)
ALLOCATE(BLCK%IA2(BLCK%M+1),STAT=IRCODE3)
IRCODE = IRCODE1 + IRCODE2 + IRCODE3
IF (IRCODE /= 0) THEN
WRITE(6,*) 'Error allocating BLCK'
CALL BLACS_ABORT(ICTXT,-1)
STOP
ENDIF
!
! In this simple example, all processes have a copy of
! the global sparse matrix, A, the global rhs vector, B,
! and the global initial guess vector, X.
!
! Each process will call PSPINS as many times as necessary
! to insert the local rows it owns.
!
! Each process will call PGEINS as many times as necessary
! to insert the local elements it owns.
!
DO GLOBAL_INDX = 1, NROW
CALL PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
!
! In this simple example, NV will always be 1
! since there will not be duplicate coefficients
!
DO NV_COUNT = 1, NV
GLOBAL_INDX_OWNER = PV(NV_COUNT)
IF (GLOBAL_INDX_OWNER == MYROW) THEN
BLCK%IA2(1) = 1
BLCK%IA2(2) = 1
DO J = IA(GLOBAL_INDX), IA(GLOBAL_INDX+1)-1
BLCK%AS(BLCK%IA2(2)) = A_GLOBAL(J)
BLCK%IA1(BLCK%IA2(2)) = JA(J)
BLCK%IA2(2) =BLCK%IA2(2) + 1
ENDDO
CALL PSPINS(A,GLOBAL_INDX,1,BLCK,DESC_A)
CALL PGEINS(B,B_GLOBAL(GLOBAL_INDX:GLOBAL_INDX),
& DESC_A,GLOBAL_INDX)
CALL PGEINS(X,XINIT_GLOBAL(GLOBAL_INDX:GLOBAL_INDX),
& DESC_A,GLOBAL_INDX)
ENDIF
END DO
END DO
! Assemble A and DESC_A
AFMT = 'DEF'
ATYPE = 'GEN'
CALL PSPASB(A,DESC_A,MTYPE=ATYPE,
& STOR=AFMT,DUPFLAG=2,INFO=IERR)
IF (IERR /= 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in assembly :',IERR
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
! Assemble B and X
CALL PGEASB(B,DESC_A)
CALL PGEASB(X,DESC_A)
!
! Deallocate BLCK
!
IF (ASSOCIATED(BLCK%AS)) DEALLOCATE(BLCK%AS)
IF (ASSOCIATED(BLCK%IA1)) DEALLOCATE(BLCK%IA1)
IF (ASSOCIATED(BLCK%IA2)) DEALLOCATE(BLCK%IA2)
!
! Deallocate Work vector
!
IF (ASSOCIATED(PV)) DEALLOCATE(PV)
!
! Preconditioning
!
! We are using ILU for the preconditioner; PESSL
! will allocate PRC.
!
IPREC = 2
CALL PSPGPR(IPREC,A,PRC,DESC_A,INFO=IERR)
IF (IERR /= 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in preconditioner :',IERR
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
!
! Iterative Solver - use the BICGSTAB method
!
ITMAX = 1000
EPS = 1.D-8
METHD = 1
ISTOPC = 1
ITRACE = 0
IPARM = 0
IPARM(1) = METHD
IPARM(2) = ISTOPC
IPARM(3) = ITMAX
IPARM(4) = ITRACE
RPARM = 0.0D0
RPARM(1) = EPS
CALL PSPGIS(A,B,X,PRC,DESC_A,IPARM=IPARM,RPARM=RPARM,
& INFO=IERR)
IF (IERR /= 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in solver :',IERR
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
ITER = IPARM(5)
ERR = RPARM(2)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Number of iterations : ',ITER
WRITE(6,*) 'Error on exit : ',ERR
END IF
!
! Each process prints their local piece of the solution vector
!
IF (IAM.EQ.0) THEN
Write(6,*) 'Solution Vector X'
END IF
LOCAL_INDX = 1
Do GLOBAL_INDX = 1, NROW
CALL PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
!
! In this simple example, NV will always be 1
! since there will not be duplicate coefficients
!
DO NV_COUNT = 1, NV
GLOBAL_INDX_OWNER = PV(NV_COUNT)
IF (GLOBAL_INDX_OWNER == MYROW) THEN
Write(6,*) GLOBAL_INDX, X(LOCAL_INDX)
LOCAL_INDX = LOCAL_INDX +1
ENDIF
END DO
END DO
!
! Deallocate the vectors, the sparse matrix, and
! the preconditioner data structure.
! Finally, deallocate the descriptor vector
!
CALL PGEFREE(B, DESC_A)
CALL PGEFREE(X, DESC_A)
CALL PSPFREE(A, DESC_A)
CALL PSPFREE(PRC, DESC_A)
CALL PADFREE(DESC_A)
!
! Terminate the process grid and the BLACS
!
CALL BLACS_GRIDEXIT(ICTXT)
CALL BLACS_EXIT(0)
END PROGRAM EXAMPLE90
This section contains the Fortran 77 sparse linear algebraic equation
subroutine descriptions and their sparse utility subroutines.
This sparse utility subroutine initializes an array descriptor, which is
needed to establish a mapping between the global general sparse matrix
A and its corresponding distributed memory location.
| Fortran
| CALL PADINIT (n, parts, desc_a,
icontxt)
|
| C and C++
| padinit (n, parts, desc_a, icontxt);
|
- n
- is the order of the global general sparse matrix A and the size
of the index space.
Scope: global
Specified as: a fullword integer, where:
n > 0.
- parts
- is a user-supplied subroutine that specifies a mapping between a global
index for an element in the global general sparse matrix A and its
corresponding storage location on one or more processes.
Sample parts subroutines for common types of data distributions
are shown in "Sample PARTS Subroutine".
For details about how you must define the PARTS subroutine, see "Programming Considerations for the Parts Subroutine (Fortran 90 and Fortran 77)".
Scope: global
Specified as: parts must be declared as an external
subroutine in your application program. It can be whatever name you choose.
- desc_a
-
is the array descriptor for the global general sparse matrix A.
DESC_A(11), which is the length of the array descriptor, DLEN, is the only
element that you must specify. To determine a sufficient value, see "Array Descriptor".
Specified as: an array of length DLEN, containing fullword integers.
- icontxt
- is the BLACS context parameter.
Scope: global
Specified as: a fullword integer that was returned in a prior call to
BLACS_GRIDINIT or BLACS_GRIDMAP.
- desc_a
- is the array descriptor for the global general sparse matrix A.
This subroutine initializes the remaining elements in the array descriptor
desc_a. The elements of desc_a are updated with subsequent
calls to PDSPINS and finalized with a call to PDSPASB.
Table 28 describes some of the elements of the array descriptor that you may want to
reference. Your application programs should not modify the elements of the
array descriptor directly. The elements should only be updated with calls to
PDSPINS and PDSPASB.
Returned as: an array of length DLEN, containing fullword integers.
- Before you call this subroutine, you must create a
np × 1 process grid, where np is the number of
processes.
- N_ROW is stable after you have placed a call to this subroutine. N_COL is
stable after you have placed a call to PDSPASB. For more details about N_ROW,
N_COL, and other elements of desc_a, see Table 28.
None.
None.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- n <= 0
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- n differs.
- pv or nv, output from the user-supplied parts
subroutine, was not valid. For valid values, see the appropriate argument
description in "Programming Considerations for the Parts Subroutine (Fortran 90 and Fortran 77)".
- DLEN is too small. For valid values, see "Array Descriptor".
This sparse utility subroutine initializes the local part of a general
sparse matrix A.
| Fortran
| CALL PDSPINIT (as, ia1, ia2, infoa,
desc_a)
|
| C and C++
| pdspinit (as, ia1, ia2, infoa,
desc_a);
|
- as
- See 'On Return'.
- ia1
- See 'On Return'.
- ia2
- See 'On Return'.
- infoa
- is an array, referred to as INFOA, providing more information
about the general sparse matrix A. You must specify
INFOA(1) through INFOA(3), as follows:
- INFOA(1) is the length of the array AS, where:
INFOA(1) >= max(2,nnze).
- INFOA(2) is the length of the array IA1,
where:
INFOA(2) >= max(3,(nnze+N_ROW)).
- INFOA(3) is the length of the array IA2,
where:
INFOA(3) >= max(3,(nnze+N_COL)).
- INFOA(4) through INFOA(30) are reserved for internal
use.
nnze is the number of non-zero elements (including duplicate
coefficients) in the local part of the global general sparse matrix
A.
Specified as: an array of length 30, containing fullword integers.
- desc_a
- is the array descriptor for a global general sparse matrix A
that is produced on a preceding call to PADINIT.
Specified as: an array of length DLEN, containing fullword integers.
- as
- is the local part, containing some internal values that are initialized by
Parallel ESSL, of the global general sparse matrix A.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the local part, containing some internal values that are initialized by
Parallel ESSL, of the sparse matrix indices.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the local part, containing some internal values that are initialized by
Parallel ESSL, of the sparse matrix indices.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the array INFOA updated with some internal values that are
set by Parallel ESSL.
Returned as: an array of length 30, containing fullword integers.
- desc_a
- is the updated array descriptor for the global general sparse matrix
A.
Returned as: an array of length DLEN, containing fullword integers.
- Before you call this subroutine, you must have called PADINIT.
- For details about some of the elements stored in desc_a, see Table 28.
- For details about some of the elements stored in infoa, see Table 27.
None
None.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- INFOA(1) < 2; that is, the size of
AS < 2
- INFOA(2) < 3; that is, the size of
IA1 < 3
- INFOA(3) < 3; that is, the size of
IA2 < 3
This sparse utility subroutine is used by each process to insert all blocks
of data it owns into its local part of the general sparse matrix A.
| Fortran
| CALL PDSPINS (as, ia1, ia2, infoa,
desc_a, ia, ja, blcks, ib1,
ib2, infob)
|
| C and C++
| pdspins (as, ia1, ia2, infoa,
desc_a, ia, ja, blcks, ib1,
ib2, infob);
|
- as
- is the local part of the global general sparse matrix A that is
produced on a preceding call to PDSPINIT or previous call(s) to this
subroutine.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the local part of array IA1 that is produced on a preceding
call to PDSPINIT or previous call(s) to this subroutine.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the local part of the array IA2 that is produced on a
preceding call to PDSPINIT or previous call(s) to this subroutine.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the array INFOA that is produced on a preceding call to
PDSPINIT or previous call(s) to this subroutine.
Specified as: an array of length 30, containing fullword integers.
- desc_a
- is the array descriptor for a global general sparse matrix A
that is produced on a preceding call to PDSPINIT or previous call(s) to this
subroutine.
Specified as: an array of length DLEN, containing fullword integers.
- ia
- is the first global row index of the general sparse matrix A
that receives data from the submatrix BLCK.
Scope: local
Specified as: a fullword integer;
1 <= ia <= M.
- ja
- is the first global column index of the general sparse matrix A
that receives data from the submatrix BLCK.
Scope: local
Specified as: a fullword integer, where:
ja = 1.
- blcks
- is the local part of the sparse submatrix BLCK, referred to as
BLCKS, to be inserted into the global general sparse matrix
A. Each call to this subroutine inserts one contiguous block of
rows into the local part of the sparse matrix corresponding to the global
submatrix
Aia:ia+INFOB(6)-1,
ja:ja+INFOB(7)-1. This
subroutine only can insert blocks of data it owns into its local part of the
general sparse matrix A.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOB(1), containing long-precision real numbers.
- ib1
- is an array, referred to as IB1, containing column numbers of
each non-zero element in the submatrix BLCK.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOB(2), containing fullword integers.
- ib2
- is the array, referred to as IB2, containing the starting
positions of each row of the submatrix BLCK in array
BLCKS and one position past the end of BLCKS.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOB(3), containing fullword integers:
- IB2(1) = 1
- IB2(INFOB(6)+1) = 1+nz and
nz is the actual number of non-zero elements in the
submatrix BLCK.
- infob
- is an array, referred to as INFOB, providing information about
the submatrix BLCK. You must specify INFOB(1) through
INFOB(7), as follows:
- INFOB(1) is the length of the array BLCKS,
where: INFOB(1) >= nz.
- INFOB(2) is the length of the array IB1,
where: INFOB(2) >= nz.
- INFOB(3) is the length of the array IB2,
where: INFOB(3) >= (INFOB(6)+1).
- INFOB(4) is the storage format of submatrix BLCK,
where:
If INFOB(4) = 1, submatrix BLCK is stored by
rows.
- INFOB(5) indicates the matrix type, where:
If INFOB(5) = 1, BLCK is a general sparse
matrix.
- INFOB(6) is the number of local rows in the submatrix
BLCK, where:
1 <= INFOB(6) <= N_ROW.
- INFOB(7) is an upper bound on the number of local columns in
the submatrix BLCK, where:
1 <= INFOB(7) <= n. n is the
order of the global general sparse matrix A.
- INFOB(8) through INFOB(30) are reserved.
Specified as: an array of length 30, containing fullword integers.
- as
- is the updated local part of the global general sparse matrix
A, updated with data from the submatrix BLCK.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the updated local part of array IA1.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the updated local part of the array IA2.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the updated local part of array INFOA.
Returned as: an array of length 30, containing fullword integers.
- desc_a
- is the updated array descriptor for the global general sparse matrix
A.
Returned as: an array of length DLEN, containing fullword integers.
- Before you call this subroutine, you must have called PADINIT and
PDSPINIT.
- Arguments BLCK and A must not have common elements;
otherwise, results are unpredictable.
- For details about some of the elements stored in desc_a, see Table 28.
- For details about some of the elements stored in infoa or
infob, see Table 27.
- The submatrix BLCK must be stored by rows; that is
INFOB(4) = 1. For information about the storage-by-rows
storage mode, see the ESSL Version 3 Guide and Reference.
- Each process has to call PDSPINS as many times as necessary to insert the
local rows it owns. It is also possible to call PDSPINS multiple times to
insert different or duplicate coefficients of the same local row it owns. For
information on how duplicate coefficients are handled, see the
dupflag argument description in PDSPASB. For an example of inserting
coefficients of the same local row, see "Example".
None.
None.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- ja <> 1
- desc_a is not valid.
- The sparse matrix A is not valid.
- INFOB(4) <> 1
- INFOB(5) <> 1
- INFOB(6) < 1 or
INFOB(6) > N_ROW
- INFOB(7) < 1 or
INFOB(7) > n
- ia < 1 or ia > M
- One or more rows to be inserted into submatrix A does not
belong to the process.
- DLEN is too small. For valid values, see "Array Descriptor".
- INFOB(1) < nz; that is, the size of
BLCKS < nz
- INFOB(2) < nz; that is, the size of
IB1 < nz
- INFOB(3) < (INFOB(6)+1); that is,
the size of IB2 < (INFOB(6)+1)
- INFOA(1) < max(2,nnze); that is, the size
of AS < max(2,nnze)
- INFOA(2) < max(3,(nnze+N_ROW)); that
is, the size of IA1 < max(3,(nnze+N_ROW))
- INFOA(3) < max(3,(nnze+N_COL)); that
is, the size of IA2 < max(3,(nnze+N_COL))
This piece of an example shows how to insert coefficients
into the same GLOB_ROW row by calling PDSPINS multiple times. This example
would be useful in finite element applications, where PDSPINS inserts one
element at a time into the global matrix, but more than one element may
contribute to the same matrix row. In this case, PDSPINS is called with the
same value of ia by all the elements contributing to that row.
For a complete example, see Example--Using the Fortran 77 Sparse Subroutines.
.
.
.
DO GLOB_ROW = 1, N
RINFOA(1) = 20
RINFOA(2) = 20
RINFOA(3) = 20
RINFOA(4) = 1
RINFOA(5) = 1
RINFOA(6) = 1
RINFOA(7) = N
RIA2(1) = 1
RIA2(2) = 2
IA = GLOB_ROW
C ! (x-1,y)
RAS(1) = COEFF(X-1,Y,X,Y)
RIA1(1) = IDX(X-1,Y)
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
C ! (x,y-1)
RAS(1) = COEFF(X,Y-1,X,Y)
RIA1(1) = IDX(X,Y-1)
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
C ! (x,y)
RAS(1) = COEFF(X,Y,X,Y)
RIA1(1) = IDX(X,Y)
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
C ! (x,y+1)
RAS(1) = COEFF(X,Y+1,X,Y)
RIA1(1) = IDX(X,Y+1)
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
C ! (x+1,y)
RAS(1) = COEFF(X+1,Y,X,Y)
RIA1(1) = IDX(X+1,Y)
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
END DO
.
.
.
This sparse utility subroutine is used by each process to insert all blocks
of data it owns into its local part of the dense vector.
| Fortran
| CALL PDGEINS (nx, x, ldx, ix,
jx, mb, nb, blcks, ldb,
desc_a)
|
| C and C++
| pdgeins (nx, x, ldx, ix, jx,
mb, nb, blcks, ldb, desc_a);
|
- nx
- is the number of columns in the local dense vector.
Scope: local
Specified as: fullword integer; nx = 1.
- x
- See 'On Return'.
- ldx
- is the local leading dimension of the local array.
Scope: local
Specified as: fullword integer;
ldx >= max(1,N_ROW).
- ix
- is the first global row index of the dense vector that receives data from
the submatrix BLCK.
Scope: local
Specified as: a fullword integer;
1 <= ix <= M.
- jx
- is the first global column index of the dense vector that receives data
from the submatrix BLCK.
Scope: local
Specified as: fullword integer; jx = 1.
- mb
- is the number of local rows to be inserted into the dense vector.
Scope: local
Specified as: fullword integer;
1 <= mb <= min(N_ROW,ldb).
- nb
- is the number of local columns to be inserted into the dense vector.
Scope: local
Specified as: fullword integer; nb = 1.
- blcks
- is the local part, referred to as BLCKS, of the submatrix
BLCK, containing the coefficients to be inserted into the dense
vector. Each call to this subroutine inserts one contiguous block of data into
the local part of the dense vector corresponding to the global submatrix
Xix:ix+mb-1,jx:jx+nb-1.
Scope: local
Specified as: an ldb by (at least) nb array,
containing long-precision real numbers.
- ldb
- is the local leading dimension for the local array BLCKS.
Scope: local
Specified as: fullword integer;
ldb >= max(1,mb).
- desc_a
- is the array descriptor that is produced on a preceding call to PADINIT,
PDSPINIT, or PDSPINS.
Specified as: an array of length DLEN, containing fullword integers.
- x
- is the updated local part of the dense vector.
Scope: local
Returned as: an ldx by (at least) nx array,
containing long-precision real numbers.
- Before you call this subroutine, you must have called PADINIT.
- You do not need a separate array descriptor for a dense vector because it
must conform to the size of matrix A. For details about some of the
elements stored in desc_a, see Table 28.
- This subroutine must be called for:
- Vector b containing the right-hand side.
- Vector x containing the initial guess to the solution.
- Each process has to call PDGEINS as many times as necessary to insert the
local elements it owns. It is also possible to call PDGEINS multiple times to
insert different coefficients of the same local row it owns. Duplicate
coefficients are overwritten.
None
- None.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- nb <> 1
- nx <> 1
- jx <> 1
- desc_a is not valid.
- ldx < max(1,N_ROW)
- 1 < mb or mb > N_ROW
- ldb < max(1,mb)
- ix < 1 or ix > M
- One or more elements to be inserted into the submatrix BLCK
does not belong to the process.
This sparse utility subroutine uses the output from PDSPINS to assemble the
global general sparse matrix A and its array descriptor
desc_a.
| Fortran
| CALL PDSPASB (as, ia1, ia2, infoa,
desc_a, mtype, stor, dupflag,
info)
|
| C and C++
| pdspasb (as, ia1, ia2, infoa,
desc_a, mtype, stor, dupflag,
info);
|
- as
- is the local part of the global general sparse matrix A that is
produced by previous call(s) to PDSPINS.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the local part of array IA1 that is produced by previous
call(s) to PDSPINS.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the local part of array IA2 that is produced by previous
call(s) to PDSPINS.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the array INFOA that is produced by previous call(s) to
PDSPINS.
Specified as: an array of length 30, containing fullword integers.
- desc_a
- is the array descriptor for the global general sparse matrix A
that is produced by previous call(s) to PDSPINS.
Specified as: an array of length DLEN, containing fullword integers.
- mtype
- indicates the the form of the global sparse matrix A used,
where:
If mtype = 'GEN', A is a general sparse
matrix.
Scope: global
Specified as: a character variable of length 5;
mtype = 'GEN'.
- stor
- indicates the storage mode that the global general sparse matrix
A is returned in, where:
If stor = 'DEF', this subroutine chooses an
appropriate storage mode, which is an internal format accepted by the
preconditioner and solver subroutines, for storing the global general sparse
matrix A on output.
If stor = 'CSR', the global general sparse matrix
A is stored in the storage-by-rows storage mode on output.
Scope: global
Specified as: a character variable of length 5;
stor = 'DEF' or 'CSR'.
- dupflag
- is a flag indicating how to use coefficients that are specified more than
once on the same process; that is, duplicate coefficients within the same
local part of the matrix A:
If dupflag = 0, this subroutine uses the first of the
duplicate coefficients.
If dupflag = 1, this subroutine adds all the duplicate
coefficients with the same indices.
If dupflag = 2, this subroutine raises an error condition
indicating that there are unexpected duplicate coefficients.
Scope: global
Specified as: a fullword integer; dupflag = 0, 1, or
2.
- info
- See 'On Return'.
- as
- is the updated local part of array AS of the global general
sparse matrix A, where:
If stor = 'DEF', this subroutine chooses an
appropriate storage mode, which is an internal format accepted by the
preconditioner and solver subroutines, for storing the global general sparse
matrix A on output.
If stor = 'CSR', the global general sparse matrix
A is stored in the storage-by-rows storage mode on output.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the updated local part of array IA2.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the updated local part of array IA2.
Scope: local
Returned as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the updated array INFOA.
Returned as: an array of length 30, containing fullword integers.
- desc_a
- is the final updated array descriptor for the global general sparse matrix
A.
Returned as: an array of length DLEN, containing fullword integers.
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, then one or more of the following
computational errors occurred and the appropriate error messages were issued,
indicating an error exit, where:
- If info = 1, the sparse matrix A contains
duplicate coefficients.
- If info = 2, the sparse matrix A contains
empty row(s).
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, info must be passed by reference.
- This subroutine accepts mixed case letters for the mtype and
stor arguments.
- Before you call this subroutine, you must have called PDSPINS as many
times as needed; that is, you must have completed building the matrix with
call(s) to PDSPINS before you place a call to this subroutine.
- Your program must declare mtype and stor to be
characters of length 5 with blanks padded to the right. C programs can use the
fifth character for the null terminator.
- For details about some of the elements stored in desc_a, see Table 28.
- For details about some of the elements stored in infoa, see Table 27.
The sparse matrix A contains duplicate
coefficients or empty row(s). For details, see the description of the
info argument.
- Unable to allocate work space.
- Unable to deallocate work space.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a is not valid.
- The sparse matrix A is not valid.
- mtype <> 'GEN'
- stor <> 'DEF' or 'CSR'
- dupflag <> 0, 1, or 2
- Some local rows in the sparse matrix A are missing.
- DLEN is too small. For valid values, see "Array Descriptor".
- INFOA(1) < max(2,nnze); that is, the size
of AS < max(2,nnze)
- INFOA(2) < max(3,(nnze+N_ROW)); that
is, the size of IA1 < max(3,(nnze+N_ROW))
- INFOA(3) < max(3,(nnze+N_COL)); that
is, the size of IA2 < max(3,(nnze+N_COL))
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- mtype differs.
- stor differs.
- dupflag differs.
This sparse utility subroutine assembles a dense vector.
| Fortran
| CALL PDGEASB (nx, x, ldx, desc_a)
|
| C and C++
| pdgeasb (nx, x, ldx, desc_a);
|
- nx
- is the number of columns in the local dense vector.
Scope: local
Specified as: fullword integer; nx = 1.
- x
- is the local part of the dense matrix x produced by previous
call(s) to PDGEINS.
Scope: local
Specified as: an ldx by (at least) nx array,
containing long-precision real numbers.
- ldx
- is the local leading dimension of the dense matrix.
Scope: local
Specified as: fullword integer;
ldx >= max(1,N_ROW).
- desc_a
- is the array descriptor, which was finalized in a preceding call to
PDSPASB.
Specified as: an array of length DLEN, containing fullword integers.
- x
- is the updated local part of the dense matrix.
Scope: local
Returned as: an ldx by (at least) length nx,
containing long-precision real numbers.
- Before you call this subroutine, you must have called PDGEINS as many
times as needed; that is, you must have completed building the dense vectors
with call(s) to PDGEINS before you place a call to this subroutine.
Before you call this subroutine, you must have called PDSPASB.
- You do not need a separate array descriptor for a dense vector because it
must conform to the size of matrix A. For details about some of the
elements stored in desc_a, see Table 28.
- This subroutine must be called for:
- Vector b containing the right-hand side.
- Vector x containing the initial guess to the solution.
None
None.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a is not valid.
- ldx < max(1,N_ROW)
This subroutine computes a preconditioner for the global general sparse
matrix A that should be passed unchanged to the PDSPGIS subroutine.
The preconditioners include diagonal scaling or an incomplete LU
factorization.
| Fortran
| CALL PDSPGPR (iprec, as, ia1, ia2,
infoa, prcs, lprcs, desc_a, info)
|
| C and C++
| pdspgpr (iprec, as, ia1, ia2,
infoa, prcs, lprcs, desc_a,
info);
|
- iprec
- is a flag that determines the type of preconditioning, where:
If iprec = 0, which is referred to as none,
indicates the local part of the submatrix A is not preconditioned.
PDSPGIS may not be effective in this case, unless the coefficient matrix is
well conditioned; if your input matrix is not well conditioned, you should
consider using iprec = 1 or 2.
If iprec = 1, which is referred to as diagsc,
indicates the local part of the submatrix A is preconditioned by a
local diagonal submatrix.
If iprec = 2, which is referred to as ilu,
indicates the local part of the submatrix A is preconditioned by a
local incomplete LU factorization.
It is suggested that you use a preconditioner. For an explanation, see "Notes and Coding Rules".
Scope: global
Specified as: a fullword integer, where:
iprec = 0, 1, or 2.
- as
- is the local part of the global general sparse matrix A,
finalized on a preceding call to PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the local part of array IA1 produced by a previous call to
PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the local part of array IA2 produced by a previous call to
PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the array INFOA produced by a previous call to PDSPASB.
Specified as: an array of length 30, containing fullword integers.
- prcs
- See 'On Return'.
- lprcs
- is the length of array PRCS.
Scope: local
Specified as: fullword integer, where:
- If iprec = 0, lprcs >= 10.
- If iprec = 1, lprcs >= 10+N_ROW.
- If iprec = 2,
lprcs >= 10+2(nnz)+N_ROW+N_COL+31
nnz is the number of non-zero elements (without duplicate
coefficients) in the local part of the global general sparse matrix
A.
- desc_a
- is the array descriptor for the global general sparse matrix A
that was finalized in a call to PDSPASB.
Specified as: an array of length DLEN, containing fullword integers.
- info
- See 'On Return'.
- prcs
- is the preconditioner data structure that must be pass unchanged to
PDSPGIS.
Scope: local
Returned as: a one-dimensional array of (at least) length
lprcs, containing long-precision real numbers.
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, the value stored in info
indicates the row index in the global general sparse matrix A where
the preconditioner failed.
Scope: global
Returned as: a fullword integer; info >= 0.
- Before you call this subroutine, you must have called PDGEASB and PDSPASB.
- In your C program, info must be passed by reference.
- For details about some of the elements stored in desc_a, see Table 28.
- For details about some of the elements stored in infoa see Table 27.
- The convergence rate of an iterative method as applied to a given system
of linear equations depends on the spectral properties of the coefficient
matrix of the linear system; therefore it is often convenient to apply a
linear transformation to the system such that the solution of the transformed
system is the same (in exact arithmetic) as that of the original, but the
spectral properties and the convergence behavior are more favorable. Such a
transformation is called preconditioning. If a matrix M
approximates A, then:
(M-1)Ax =
(M-1)b
is a preconditioned system and M is called a preconditioner. In
practice, the new coefficient matrix (M-1)A
is almost never formed explicitly, but rather its action is computed during
the application of the iterative method. The effectiveness of the
preconditioning operation depends on a trade-off between how well M
approximates A and how costly it is to compute and invert it; no
single preconditioner will give best overall performance under all situations.
Note finally that it is quite rare for a linear system to behave well enough
so as not to require preconditioning; indeed most linear systems originating
from the the discretization of difficult physical problems require
preconditioning to have any convergence at all.
- The preconditioner for the sparse matrix A is unstable. For
details, see the info output argument for this subroutine.
- Unable to allocate work space.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a is not valid.
- iprec <> 0, 1, or 2
- iprec = 0 and lprcs < 10
- iprec = 1 and lprcs < 10+N_ROW
- iprec = 2 and
lprcs < 10+2(nnz)+N_ROW+N_COL+31
- The storage format for A is not supported.
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- iprec differs.
This subroutine solves a general sparse linear system of equations, using
an iterative algorithm, with or without preconditioning. The methods include
the more smoothly converging variant of the CGS method (Bi-CGSTAB), conjugate
gradient squared (CGS), or transpose-free quasi-minimal residual method
(TFQMR).
See references [7], [9], [12], and [35].
| Fortran
| CALL PDSPGIS (as, ia1, ia2, infoa,
nrhs, b, ldb, x, ldx,
prcs, desc_a, iparm, rparm, info)
|
| C and C++
| pdspgis (as, ia1, ia2, infoa,
nrhs, b, ldb, x, ldx,
prcs, desc_a, iparm, rparm,
info);
|
- as
- is the local part of the global general sparse matrix A,
finalized on a preceding call to PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(1), containing long-precision real numbers.
- ia1
- is the local part of array IA1 produced by a previous call to
PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(2), containing fullword integers.
- ia2
- is the local part of array IA2 produced by a previous call to
PDSPASB.
Scope: local
Specified as: a one-dimensional array of (at least) length
INFOA(3), containing fullword integers.
- infoa
- is the array INFOA produced by a previous call to PDSPASB.
Specified as: an array of length 30, containing fullword integers.
- nrhs
- the number of right-hand sides.
Scope: global
Specified as: a fullword integer; nrhs = 1.
- b
- is the local part of the matrix b, containing the right-hand
side of the matrix problem produced on a previous call to PDGEASB.
Scope: local
Specified as: an ldb by (at least) length nrhs
array, containing long-precision real numbers.
- ldb
- is the leading dimension of the local array B.
Scope: local
Specified as: a fullword integer;
ldb >= max(1,N_ROW)
- x
- is the local part of the global vector x, containing the
initial guess to the solution of the linear system and produced on a previous
call to PDGEASB.
Scope: local
Specified as: an ldx by (at least) nrhs array,
containing long-precision real numbers.
- ldx
- is the leading dimension of the local array X.
Scope: local
Specified as: a fullword integer;
ldx >= max(1,N_ROW)
- prcs
- is the preconditioner data structure prcs produced by a previous
call to PDSPGPR.
Scope: local
Specified as: a one-dimensional array of (at least) length
lprcs, containing long-precision real numbers.
- desc_a
- is the array descriptor for the global general sparse matrix A
that was finalized in a call to PDSPASB.
Specified as: an array of length DLEN, containing fullword integers.
- iparm
- is an array of parameters, IPARM(i), where:
- IPARM(1) is the flag, methd, used to select the
iterative procedure used, where:
If IPARM(1) = 0, the following defaults are used:
- methd = 1
- istopc = 1
- itmax = 500
- itrace = 0
- eps = 10-8
If methd = 1, the more smoothly converging variant of the
CGS method, referred to as Bi-CGSTAB, is used.
If methd = 2, the conjugate gradient squared method,
referred to as CGS, is used.
If methd = 3, the transpose-free quasi-minimal residual
method, referred to as TFQMR, is used.
- IPARM(2) is the flag, istopc used to select the
stopping criterion used in the computation, where the following items are used
in the definitions of the stopping criteria below:
- epsilon is the desired relative accuracy and is stored in eps
- xj is the solution found at the j-th
iteration.
- rj and r0 are the
preconditioned residuals obtained at iterations j and 0,
respectively. (The residual at iteration j is defined as
b-Axj.)
If istopc = 1, the iterative method is stopped when:
||rj||2 /
||xj||2 < epsilon
If istopc = 2, the iterative method is stopped when:
||rj||2 /
||r0||2 < epsilon
If istopc = 3, the iterative method is stopped when:
||xj
-xj-1||2 /
||xj||2 < epsilon
| Note: |
Stopping criterion 3 performs poorly with the TFQMR method; therefore, if you
specify TFQMR (methd = 3), you should not specify stopping
criterion 3.
|
- IPARM(3) is the maximum number, itmax, of iterations
allowed.
- IPARM(4), referred to as itrace, has the following
meaning:
If itrace = 0, then itrace is ignored.
If itrace > 0, an informational message about
convergence, which is based on the stopping criterion described in
istopc, is issued at every itrace-th iteration and upon
exit.
- IPARM(5), see 'On Return'.
- IPARM(6) through IPARM(20) are reserved.
Scope: global
Specified as: an array of length 20, containing fullword integers,
where:
- methd = 1, 2, or 3
- istopc = 1, 2, or 3.
- itmax >= 0.
- itrace >= 0.
- IPARM(6) through IPARM(20) should be set to zero.
- rparm
-
is an array of parameters, RPARM(i), where:
- RPARM(1) is the relative accuracy epsilon, referred to as
eps, used in the stopping criterion.
- RPARM(2), see 'On Return'.
- RPARM(3) through RPARM(20) are reserved.
Scope: global
Specified as: an array of length 20, containing long-precision real
numbers, where:
- eps >= 0.
- RPARM(3) through RPARM(20) should be set to zero.
- info
- See 'On Return'.
- x
- is the local part of the solution vector x
Scope: local
Returned as: an array of (at least) length N_ROW, containing
long-precision real numbers.
- iparm
- is an array of parameters, IPARM(i), where:
- IPARM(2) is the number of iterations, iter, performed
by this subroutine.
Scope: global
Returned as: an array of length 20, containing fullword integers,
where:
- iter >= 0
- rparm
- is an array of parameters, RPARM(i), where:
- RPARM(2) contains the estimate of the error, err, of
the solution, according to the stopping criterion, istopc, in use.
For details, see the istopc argument description.
Scope: global
Returned as: an array of length 20, containing long-precision real
numbers, where:
- err >= 0
- info
- has the following meaning, when info is present:
If info = 0, then no input-argument errors or
computational errors occurred. This indicates a normal exit.
| Note: |
Because Parallel ESSL terminates the application if input-argument errors
occur, the setting of info is irrelevant for these errors.
|
If info > 0, then this subroutine exceeded
itmax iterations without converging. You may want to try the
following to get your matrix to converge:
- You can increase the number of iterations and call this subroutine again
without making any other changes to your program.
- You can change the requested precision and/or the stopping
criterion; your original precision requirement may be too stringent under a
given stopping criterion.
- You can use a preconditioner if you were not already doing so, or to
change the one you were using. Note also that the efficiency of the
preconditioner may depend on the data distribution strategy adopted. See "Notes and Coding Rules".
Scope: global
Returned as: a fullword integer; info >= 0.
- In your C program, info must be passed by reference.
- Before you call this subroutine, you must have called PDSPGPR.
- For details about some of the elements stored in desc_a, see Table 28.
- For details about some of the elements stored in infoa see Table 27.
- This subroutine exceeded itmax iterations without converging.
Vector x contains the approximate solution computed at the last
iteration.
| Note: |
If the preconditioner computed by PDSPGPR failed because the sparse matrix
A is unstable, the results returned by this subroutine are
unpredictable. For details, see the info output argument for PDSPGPR.
|
You may want to try the following to get your matrix to converge:
- You can increase the number of iterations and call this subroutine again
without making any other changes to your program.
- You can change the requested precision and/or the stopping
criterion; your original precision requirement may be too stringent under a
given stopping criterion.
- You can use a preconditioner if you were not already doing so, or to
change the one you were using. Note also that the efficiency of the
preconditioner may depend on the data distribution strategy adopted. See "Notes and Coding Rules".
- Unable to allocate work space.
- The BLACS context is invalid.
- This subroutine was called from outside the process grid.
- The process grid is not np × 1.
- desc_a is not valid.
- nrhs <> 1
- eps < 0.0
- methd <> 1, 2, or 3
- The preconditioner data structure prcs is not valid.
- istopc <> 1, 2, or 3
- itmax < 0
- itrace < 0
- The sparse matrix A is not valid.
- The storage format for the sparse matrix A is not supported.
- ldb < max(1,N_ROW)
- ldx < max(1,N_ROW)
- The preconditioner data structure prcs is not valid.
- Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- iparm differs.
- rparm differs.
- eps differs.
- methd differs.
- istopc differs.
- itmax differs.
- itrace differs.
- Some element(s) of prcs differ.
This example finds the solution to the linear system
Ax = b. It also contains an application program
that shows how you can use the Fortran 77 sparse linear algebraic equation
subroutines and their utilities to solve the problem shown in Example--Using the Fortran 90 Sparse Subroutines.
This application program illustrates how to use the Fortran 77 sparse
linear algebraic equation subroutines and their utilities.
!
! This program illustrates how to use the PESSL F77 Sparse Iterative
! Solver and its supporting utility subroutines. A very simple problem
! (DSRIS Example 1 from the ESSL Guide and Reference) using an
! HPF BLOCK data distribution is solved.
!
PROGRAM EXAMPLE77
IMPLICIT NONE
! Interface definition for the PARTS subroutine PART_BLOCK
INTERFACE PART_BLOCK
SUBROUTINE PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
END SUBROUTINE PART_BLOCK
END INTERFACE
! External declaration for the PARTS subroutine PART_BLOCK
EXTERNAL PART_BLOCK
! Parameters
CHARACTER*1 ORDER
CHARACTER*5 STOR
CHARACTER*5 MTYPE
INTEGER*4 IZERO, IONE, DUPFLAG, N, NNZ
PARAMETER (ORDER='R')
PARAMETER (STOR='DEF')
PARAMETER (MTYPE='GEN')
PARAMETER (IZERO=0)
PARAMETER (IONE=1)
PARAMETER (N=9)
PARAMETER (NNZ=22)
PARAMETER (DUPFLAG=2)
! Descriptor Vector
INTEGER*4, ALLOCATABLE :: DESC_A(:)
! Sparse Matrices and related information
REAL*8 AS(NNZ)
INTEGER*4 IA1(NNZ+N), IA2(NNZ+N)
INTEGER*4 INFOA(30)
REAL*8 BS(NNZ)
INTEGER*4 IB1(N+1), IB2(NNZ)
INTEGER*4 INFOB(30)
! Preconditioner Data Structure
REAL*8 PRCS(2*NNZ+2*N+41)
! Dense Vectors
REAL*8 B(N), X(N)
! BLACS parameters
INTEGER*4 NPROW, NPCOL, ICTXT, IAM, NP, MYROW, MYCOL
! Solver parameters
INTEGER*4 ITER, ITMAX, INFO, ITRACE,
& IPREC, METHD, ISTOPC, IPARM(20)
REAL*8 ERR, EPS, RPARM(20)
! We will not have duplicates so PV used by the PARTS subroutine
! PART_BLOCK only needs to be of length 1.
INTEGER PV(1)
! Other variables
INTEGER IERR
INTEGER NB, LDB, LDBG
INTEGER NX, LDX, LDXG
INTEGER NRHS
INTEGER I,J
INTEGER GLOBAL_INDX, NV_COUNT
INTEGER GLOBAL_INDX_OWNER, NV
INTEGER LOCAL_INDX
!
! Global Problem
! DSRIS Example 1 from the ESSL Guide and Reference
!
REAL*8 A_GLOBAL(NNZ),B_GLOBAL(N),XINIT_GLOBAL(N)
INTEGER JA(NNZ),IA(N+1)
DATA A_GLOBAL /2.D0,2.D0,-1.D0,1.D0,2.D0,1.D0,2.D0,-1.D0,
$ 1.D0,2.D0,-1.D0,1.D0,2.D0,-1.D0,1.D0,2.D0,
$ -1.D0,1.D0,2.D0,-1.D0,1.D0,2.D0/
DATA JA /1,2,3,2,3,1,4,5,4,5,6,5,6,7,6,7,8,
$ 7,8,9,8,9/
DATA IA /1,2,4,6,9,12,15,18,21,23/
DATA B_GLOBAL /2.D0,1.D0,3.D0,2.D0,2.D0,2.D0,2.D0,2.D0,
$ 3.D0/
DATA XINIT_GLOBAL /0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,0.D0,
$ 0.D0/
! Initialize BLACS
! Define a NP x 1 Process Grid
CALL BLACS_PINFO(IAM, NP)
CALL BLACS_GET(IZERO, IZERO, ICTXT)
CALL BLACS_GRIDINIT(ICTXT, ORDER, NP, IONE)
CALL BLACS_GRIDINFO(ICTXT, NPROW, NPCOL, MYROW, MYCOL)
!
! Allocate the descriptor vector
!
ALLOCATE(DESC_A(30 + 3*NP + 4*N + 3),STAT=IERR)
IF (IERR .NE. 0) THEN
WRITE(6,*) 'Error allocating DESC_A :',IERR
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
! Initialize some elements of the sparse matrix A
! and its descriptor vector, DESC_A
!
DESC_A(11) = SIZE(DESC_A)
CALL PADINIT(N,PART_BLOCK,DESC_A,ICTXT)
INFOA(1) = SIZE(AS)
INFOA(2) = SIZE(IA1)
INFOA(3) = SIZE(IA2)
CALL PDSPINIT(AS,IA1,IA2,INFOA,DESC_A)
!
! In this simple example, all processes have a copy of
! the global sparse matrix, A, the global rhs vector B,
! and the global initial guess vector, X
!
! Each process will call PDSPINS as many times as necessary
! to insert the local rows it owns.
!
! Each process will call PDGEINS as many times as necessary
! to insert the local elements it owns.
!
NB = 1
LDB = SIZE(B,1)
LDBG = SIZE(B_GLOBAL,1)
NX = 1
LDX = SIZE(X,1)
LDXG = SIZE(XINIT_GLOBAL,1)
DO GLOBAL_INDX = 1, N
CALL PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
!
! In this simple example, NV will always be 1
! since there will not be duplicate coefficients
!
DO NV_COUNT = 1, NV
GLOBAL_INDX_OWNER = PV(NV_COUNT)
IF (GLOBAL_INDX_OWNER == MYROW) THEN
IB2(1) = 1
IB2(2) = 1
DO J = IA(GLOBAL_INDX), IA(GLOBAL_INDX+1)-1
BS(IB2(2)) = A_GLOBAL(J)
IB1(IB2(2)) = JA(J)
IB2(2) = IB2(2) + 1
ENDDO
INFOB(1) = IB2(2) - 1
INFOB(2) = IB2(2) - 1
INFOB(3) = 2
INFOB(4) = 1
INFOB(5) = 1
INFOB(6) = 1
INFOB(7) = N
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,GLOBAL_INDX, 1,
& BS,IB1,IB2,INFOB)
CALL PDGEINS(NB,B,LDB,GLOBAL_INDX,1,1,1,
& B_GLOBAL(GLOBAL_INDX),LDBG,DESC_A)
CALL PDGEINS(NX,X,LDX,GLOBAL_INDX,1,1,1,
& XINIT_GLOBAL(GLOBAL_INDX),LDXG,DESC_A)
ENDIF
END DO
END DO
! Assemble A and DESC_A
CALL PDSPASB(AS,IA1,IA2,INFOA,DESC_A,
& MTYPE,STOR,DUPFLAG,INFO)
IF (INFO .NE. 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in assembly :',INFO
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
! Assemble B and X
CALL PDGEASB(NB,B,LDB,DESC_A)
CALL PDGEASB(NX,X,LDX,DESC_A)
!
! Preconditioning
!
! We are using ILU for the preconditioner
!
IPREC = 2
CALL PDSPGPR(IPREC,AS,IA1,IA2,INFOA,
& PRCS,SIZE(PRCS),DESC_A,INFO)
IF (INFO .NE. 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in preconditioner :',INFO
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
!
! Iterative Solver - use the BICGSTAB method
!
NRHS = 1
ITMAX = 1000
EPS = 1.D-8
METHD = 1
ISTOPC = 1
ITRACE = 0
IPARM = 0
IPARM(1) = METHD
IPARM(2) = ISTOPC
IPARM(3) = ITMAX
IPARM(4) = ITRACE
RPARM = 0.0D0
RPARM(1) = EPS
CALL PDSPGIS(AS,IA1,IA2,INFOA,NRHS,B,LDB,X,LDX,PRCS,DESC_A,
& IPARM,RPARM,INFO)
IF (INFO .NE. 0) THEN
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Error in solver :',INFO
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
END IF
ERR = RPARM(2)
ITER = IPARM(5)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Number of iterations : ',ITER
WRITE(6,*) 'Error on exit : ',ERR
END IF
!
! Each process prints their local piece of the solution vector
!
IF (IAM.EQ.0) THEN
Write(6,*) 'Solution Vector X'
END IF
LOCAL_INDX = 1
Do GLOBAL_INDX = 1, N
CALL PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
!
! In this simple example, NV will always be 1
! since there will not be duplicate coefficients
!
DO NV_COUNT = 1, NV
GLOBAL_INDX_OWNER = PV(NV_COUNT)
IF (GLOBAL_INDX_OWNER == MYROW) THEN
Write(6,*) GLOBAL_INDX, X(LOCAL_INDX)
LOCAL_INDX = LOCAL_INDX +1
ENDIF
END DO
END DO
!
! Deallocate the descriptor vector
!
DEALLOCATE(DESC_A, STAT=IERR)
IF (IERR .NE. 0) THEN
WRITE(6,*) 'Error deallocating DESC_A :',IERR
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
!
! Terminate the process grid and the BLACS
!
CALL BLACS_GRIDEXIT(ICTXT)
CALL BLACS_EXIT(0)
END PROGRAM EXAMPLE77
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]