Guide and Reference

Distributing Your Data

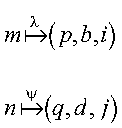
This chapter provides information on how to distribute your data for message passing programs and for HPF programs. The sections include:

• "Concepts"
• "Specifying and Distributing Data in a Message Passing Program"
• "Distributing Data in an HPF Program"

Concepts

This section describes the general concepts used in distributing data.

About Global Data Structures

Because the Parallel ESSL subroutines support the SPMD programming model, your global data structures (vectors, matrices, or sequences) must be distributed across your processes prior to calling the Parallel ESSL subroutines.

Conceptually, global data structures have a defined storage mode consistent with those used by the serial ESSL library, except for symmetric tridiagonal matrices. For Parallel ESSL, you must store symmetric tridiagonal matrices as described in this chapter in "Block-Cyclically Distributing a Symmetric Tridiagonal Matrix". For how to store all other data structures when using Parallel ESSL, you should see the appropriate section in the ESSL Version 3 Guide and Reference. The FFT-packed storage mode is a new storage mode for Parallel ESSL and is described in "Specifying Sequences for the Fourier Transforms".

Global data structures must be mapped to local (distributed memory) data structures, according to the data distribution technique supported by the Parallel ESSL subroutines that you are using. These local data structures are called local arrays.

These data distribution techniques are described throughout this chapter and apply equally to real and complex data structures.

About Process Grids

A parallel machine with k processes is often thought of as a one-dimensional linear array of processes labeled 0, 1, ..., k-1. For performance reasons, it is sometimes useful to map this one-dimensional array into a logical two-dimensional rectangular grid, which is also referred to as process grid, of processes. The process grid can have p process rows and q process columns, where p × q = k. A process can now be indexed by row and column, (i,j), where 0 <= i < p and 0 <= j < q.

Table 12 shows six processes mapped into a process grid using row-major order. For message passing subroutines, the BLACS_GRIDINIT default to map processes is row-major order. In this example, process t₃ is mapped to P₁₀.

Table 12. Six Processes Mapped to a 2 × 3 Process Grid Using Row-Major Order

p,q	0	1	2
0	t0	t1	t2
1	t3	t4	t5

Table 13 shows six processes mapped into a process grid using column-major order. For HPF subroutines, the XL HPF compiler default to map processes is column-major order. In this example, process t₃ is mapped to P₁₁.

Table 13. Six Processes Mapped to a 2 × 3 Process Grid Using Column-Major Order

p,q	0	1	2
0	t0	t2	t4
1	t1	t3	t5

All the subroutines, except the Banded Linear Algebraic Equations and Fourier transform subroutines, can view the processes as a logical one- or two-dimensional process grid. The Banded Linear Algebraic Equations support one-dimensional process grids. The Fourier transform subroutines support one-dimensional, row-oriented process grids.

Each process has local memory, and all the processes are connected by a communication network (for example, a switch or Ethernet). In most cases k is less than or equal to the number of processor nodes that your job is running on. In special cases, however, the number of processes can be greater than the number of processor nodes.

What to Do in Your Program

Prior to calling any of the subroutines, you must define your process grid and distribute your data according to the distribution technique required by the Parallel ESSL subroutine you are using.

The size and shape of the process grid and the way global data structures are distributed over the processes has a major impact on performance and scalability. For details, see "Coding Tips for Optimizing Parallel Performance". Block-cyclic data distribution generally provides good load balancing for many linear algebra computations. All subroutines support block-cyclic data distributions, except the Fourier Transforms, the HPF versions of the Banded Linear Algebraic Equations, and the HPF version of the Random Number Generation subroutine (URNG). These subroutines support only block distribution, which is a special case of block-cyclic data distribution.

Some of the message passing and HPF data distribution techniques described in this chapter are illustrated in Appendix B. "Sample Programs".

For more information using High Performance Fortran, see reference [44], and the XL High Performance Fortran manuals.

Block, Cyclic, and Block-Cyclic Data Distributions

In this section, three types of data distribution are described in algorithmic terms: block, cyclic, and block-cyclic. How these data distribution methods are used by Parallel ESSL is explained later in this chapter.

The example notation means the following:

• B represents the global block row numbers.
• D represents the global block column numbers.
• p represents the process row index.
• q represents the process column index.

Distribution Techniques

An important aspect of the data distributions described here is that independent distributions are applied over each dimension of the data structure. The algorithms presented here for the vector in one dimension can, therefore, be used for the rows and columns of a matrix, or even for data structures with more dimensions.

Consider the distribution of a vector x of M data objects (elements) over P processes. This can be described by a mapping of the global index m (0 <= m < M) of a data object to an index pair (p,i), where p (0 <= p < P) specifies the process to which the data object is mapped, and i specifies its location in the local array.

Two common distributions are the block and cyclic. The block distribution is often used when the computational load is distributed homogeneously over a regular data structure, such as a Cartesian grid. It assigns blocks of size r of the global vector to the processes. For block distribution, the mapping m --> (p, i) is defined as:

m --> (floor(m/L), m mod L)

where L = ceiling(M/P). The cyclic distribution (also known as the wrapped or scattered decomposition) is commonly used to improve load balance when the computational load is distributed inhomogeneously over a regular data structure. The cyclic distribution assigns consecutive entries of the global vector to successive processes. For cyclic distribution, the mapping m --> (p, i) is defined as:

m --> (m mod P, floor(m/P))

Examples of block and cyclic distribution are shown in Figure 1 and Figure 2, where M = 23 data objects are distributed over P = 3 processes, using r = 8 block size. As shown in the examples, there can be uneven distribution, where the last block is smaller than the others. A global block number B is shown for block distribution. For cyclic distribution, there is no concept of block numbers.

Figure 1. Block Distribution

m	0 1 2 3 4 5 6 7	8 9 10 11 12 13 14 15	16 17 18 19 20 21 22
p	0 0 0 0 0 0 0 0	1 1 1 1 1 1 1 1	2 2 2 2 2 2 2
i	0 1 2 3 4 5 6 7	0 1 2 3 4 5 6 7	0 1 2 3 4 5 6
B	0 0 0 0 0 0 0 0	1 1 1 1 1 1 1 1	2 2 2 2 2 2 2

Following are HPF statements you could use to perform this block distribution of your data:

!HPF$ PROCESSORS P(3)
!HPF$ DISTRIBUTE X (BLOCK) ONTO P

Figure 2. Cyclic Distribution

m	0 1 2	3 4 5	6 7 8	9 10 11	12 13 14	15 16 17	18 19 20	21 22
p	0 1 2	0 1 2	0 1 2	0 1 2	0 1 2	0 1 2	0 1 2	0 1
i	0 0 0	1 1 1	2 2 2	3 3 3	4 4 4	5 5 5	6 6 6	7 7

Following are HPF statements you could use to perform this cyclic distribution of your data:

!HPF$ PROCESSORS P(3)
!HPF$ DISTRIBUTE X (CYCLIC) ONTO P

The block-cyclic distribution is a generalization of the block and cyclic distributions, in which blocks of r consecutive data objects are distributed cyclically over the p processes. This can be described by a mapping of the global index m (0 <= m < M) of a data object to an index triplet (p,b,i), where p (0 <= p < P) specifies the process to which the data object is mapped, b is the block number in process p, and i is the location in the block. For block-cyclic distribution, the mapping m --> (p, b, i) is defined as:

m --> (floor((m mod T)/r), floor(m/T), m mod r)

where T = rP. (It should be noted that this reverts to the cyclic distribution when r = 1 and a block distribution when r = L.) The inverse mapping to a global index (p, b, i) --> m is defined by:

(p, b, i) --> Br+i = pr+bT+i

where B = p+bP is the global block number. An example of block-cyclic distribution is shown in Figure 3, where M = 23 data objects are distributed over P = 3 processes, using r = 2 block size. As shown in the example, there can be uneven distribution, where the last block is smaller than the others. The inverse mapping is shown in the second part of the example. (This shows what is stored in the local array on each of the three processes.)

Figure 3. Block-Cyclic Distribution

m	0 1 2 3 4 5	6 7 8 9 10 11	12 13 14 15 16 17	18 19 20 21 22
p	0 0 1 1 2 2	0 0 1 1 2 2	0 0 1 1 2 2	0 0 1 1 2
b	0 0 0 0 0 0	1 1 1 1 1 1	2 2 2 2 2 2	3 3 3 3 3
i	0 1 0 1 0 1	0 1 0 1 0 1	0 1 0 1 0 1	0 1 0 1 0
B	0 0 1 1 2 2	3 3 4 4 5 5	6 6 7 7 8 8	9 9 10 10 11

Figure 4. Inverse Mapping of Block-Cyclic Distribution

m	0 1 6 7 12 13 18 19	2 3 8 9 14 15 20 21	4 5 10 11 16 17 22
p	0 0 0 0 0 0 0 0	1 1 1 1 1 1 1 1	2 2 2 2 2 2 2
b	0 0 1 1 2 2 3 3	0 0 1 1 2 2 3 3	0 0 1 1 2 2 3
i	0 1 0 1 0 1 0 1	0 1 0 1 0 1 0 1	0 1 0 1 0 1 0
B	0 0 3 3 6 6 9 9	1 1 4 4 7 7 10 10	2 2 5 5 8 8 11

Following are HPF statements you could use to perform this block-cyclic distribution of your data:

!HPF$ PROCESSORS P(3)
!HPF$ DISTRIBUTE X (CYCLIC(2)) ONTO P

In decomposing an m × n matrix, A, independent block-cyclic distributions are applied in the row and column directions. Thus, suppose the matrix rows are distributed with block size r over P processes by the lambda_r,P block-cyclic mapping, and the matrix columns are distributed with block size s over Q processes by the psi_s,Q block-cyclic mapping. Then the matrix element indexed globally by (m, n) is mapped as follows:

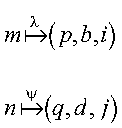
The distribution of the matrix can be regarded as the tensor product of the row and column distributions, which can be expressed as:

(m, n) --> ((p, q),(b, d),(i, j))

The block-cyclic matrix distribution expressed above distributes blocks of size r × s to a grid of P × Q processes.

An example of block-cyclic distribution of an m × n = 16 × 30 matrix with block size r × s = 3 × 4 and a P × Q = 2 × 3 process grid is shown in Figure 5 and Figure 6. The numbers in the leftmost column and on the top of the matrix represent the global row and column numbers B and D, respectively. Figure 5 shows the assignment of global blocks (B,D) to processes (P,Q). Figure 6 shows which global blocks each process contains.

In this example, the global matrix dimensions are not divisible by the respective block sizes. All the row blocks are of size 3, except the last row block, which only contains 1 row. All column blocks are of size 4, except the last column block, which contains 2 columns. For example, global block (5,0) is 1 × 4, global block (1,7) is 3 × 2, and global block (0,0) is 3 × 4. The global block (5,7) is 1 × 2. The asterisk (*) in Figure 5 denotes which global blocks contain left over data; that is, the blocks that are not 3 × 4.

Figure 5. Block Distribution Over a 2 by 3 Process Grid

B,D	0	1	2	3	4	5	6	7
0	P00	P01	P02	P00	P01	P02	P00	P01*
1	P10	P11	P12	P10	P11	P12	P10	P11*
2	P00	P01	P02	P00	P01	P02	P00	P01*
3	P10	P11	P12	P10	P11	P12	P10	P11*
4	P00	P01	P02	P00	P01	P02	P00	P01*
5	P10*	P11*	P12*	P10*	P11*	P12*	P10*	P11*

Figure 6. Data Distribution from a Process Point-of-View

B,D	0	3	6	1	4	7	2	5
0						*
2		P00			P01	*		P02
4						*
1						*
3		P10			P11	*		P12
5	*	*	*	*	*	*	*	*

Figure 7. Distributed Matrix Elements from a Process Point-of-View

B,D	0	3	6	1	4	7	2	5
0	a0:2,0:3	a0:2,12:15	a0:2,24:27	a0:2,4:7	a0:2,16:19	a0:2,28:29*	a0:2,8:11	a0:2,20:23
2	a6:8,0:3	a6:8,12:15	a6:8,24:27	a6:8,4:7	a6:8,16:19	a6:8,28:29*	a6:8,8:11	a6:8,20:23
4	a12:14,0:3	a12:14,12:15	a12:14,24:27	a12:14,4:7	a12:14,16:19	a12:14,28:29*	a12:14,8:11	a12:14,20:23
1	a3:5,0:3	a3:5,12:15	a3:5,24:27	a3:5,4:7	a3:5,16:19	a3:5,28:29*	a3:5,8:11	a3:5,20:23
3	a9:11,0:3	a9:11,12:15	a9:11,24:27	a9:11,4:7	a9:11,16:19	a9:11,28:29*	a9:11,8:11	a9:11,20:23
5	a15,0:3*	a15,12:15*	a15,24:27*	a15,4:7*	a15,16:19*	a15,28:29*	a15,8:11*	a15,20:23*

Following are HPF statements you could use to perform this block-cyclic distribution of your data:

!HPF$ PROCESSORS P(2,3)
!HPF$ DISTRIBUTE A (CYCLIC(3),CYCLIC(4)) ONTO P

Special Usage

The block-cyclic distribution can reproduce most of the data distributions commonly used in linear algebra computations on parallel computers. Some examples are:

• Block distribution in the row direction is obtained by Q = 1 and r = ceiling(M/P).

• Block distribution in the column direction is obtained by P = 1 and s = ceiling(N/Q).

• Block-cyclic distribution in the row direction is obtained by Q = 1 and r < ceiling(M/P). (You might use this for distributing a single block column to pass to Parallel ESSL.)

• Block-cyclic distribution in the column direction is obtained by P = 1 and s < ceiling(N/Q). (You might use this for distributing a single block row to pass to Parallel ESSL.)

• To achieve fine granularity of distribution in the following directions, specify:
  • For the row direction, r = 1
  • For the column direction, s = 1
  • In both directions, r = 1 and s = 1

• To achieve coarse granularity of distribution in the following directions, specify:
  • For the row direction, r = ceiling(M/P).
  • For the column direction, s = ceiling(N/Q).
  • In both directions, r = ceiling(M/P) and s = ceiling(N/Q).

This section provided a detailed description of the distribution of vectors--one-dimensional data structures. Those same techniques were then applied to matrices--two-dimensional data structures--in the row and column directions. If you have data structures with three or more dimensions, you can use these same techniques by applying them in the direction of each dimension. For example, the block distribution of a three-dimensional sequence is described in "Three-Dimensional Sequences".