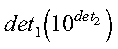
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 92.
This section provides some key points about using the linear least squares subroutines.
If you want to use a singular value decomposition method to compute the minimal norm linear least squares solution of AX is congruent to B, calls to SGESVF or DGESVF should be followed by calls to SGESVS or DGESVS, respectively.
This section contains the dense linear algebraic equation subroutine descriptions.
This subroutine factors a square general matrix A using Gaussian
elimination with partial pivoting. To solve the system of equations with one
or more right-hand sides, follow the call to these subroutines with one or
more calls to SGES/SGESM, DGES/DGESM, CGES/CGESM, or ZGES/ZGESM, respectively.
To compute the inverse of matrix A, follow the call to these
subroutines with a call to SGEICD or DGEICD, respectively.
| A | Subroutine |
| Short-precision real | SGEF |
| Long-precision real | DGEF |
| Short-precision complex | CGEF |
| Long-precision complex | ZGEF |
| Note: | The output from these factorization subroutines should be used only as input to the following subroutines for performing a solve or inverse: SGES/SGESM/SGEICD, DGES/DGESM/DGEICD, CGES/CGESM, and ZGES/ZGESM, respectively. |
| Fortran | CALL SGEF | DGEF | CGEF | ZGEF (a, lda, n, ipvt) |
| C and C++ | sgef | dgef | cgef | zgef (a, lda, n, ipvt); |
| PL/I | CALL SGEF | DGEF | CGEF | ZGEF (a, lda, n, ipvt); |
The matrix A is factored using Gaussian elimination with partial pivoting to compute the LU factorization of A, where:
The transformed matrix A contains U in the upper triangle. In its strict lower triangle, it contains the multipliers necessary to construct, with the help of ipvt, a matrix L, such that A = LU.
If n is 0, no computation is performed. See references [36] and [38].
Unable to allocate internal work area.
Matrix A is singular.
This example shows a factorization of a real general matrix A of order 9.
A LDA N IPVT
| | | |
CALL SGEF( A , 9 , 9 , IPVT )
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 |
| 4.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 0.0 5.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 |
A = | 0.0 0.0 6.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 0.0 0.0 0.0 7.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 8.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 9.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 10.0 11.0 12.0 |
* *
* *
| 4.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.0000 0.0000 0.0000 |
| 0.0000 5.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.0000 0.0000 |
| 0.0000 0.0000 6.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.0000 |
| 0.0000 0.0000 0.0000 7.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
A = | 0.0000 0.0000 0.0000 0.0000 8.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 9.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 10.0000 11.0000 12.0000 |
| 0.2500 0.1500 0.1000 0.0714 0.0536 -0.0694 -0.0306 0.1806 0.3111 |
| 0.2500 0.1500 0.1000 0.0714 -0.0714 -0.0556 -0.0194 0.9385 -0.0031 |
* *
IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9)
This example shows a factorization of a complex general matrix A of order 4.
A LDA N IPVT
| | | |
CALL CGEF( A , 4 , 4 , IPVT )
* *
| (1.0, 2.0) (1.0, 7.0) (2.0, 4.0) (3.0, 1.0) |
A = | (2.0, 0.0) (1.0, 3.0) (4.0, 4.0) (2.0, 3.0) |
| (2.0, 1.0) (5.0, 0.0) (3.0, 6.0) (0.0, 0.0) |
| (8.0, 5.0) (1.0, 9.0) (6.0, 6.0) (8.0, 1.0) |
* *
* *
| (8.0000, 5.0000) (1.0000, 9.0000) (6.0000, 6.0000) (8.0000, 1.0000) |
A = | (0.2022, 0.1236) (1.9101, 5.0562) (1.5281, 2.0449) (1.5056, -0.1910) |
| (0.2360, -0.0225) (-0.0654, -0.9269) (-0.3462, 6.2692) (-1.6346, 1.3269) |
| (0.1798, -0.1124) (0.2462, 0.1308) (0.4412, -0.3655) (0.2900, 2.3864) |
* *
IPVT = (4, 4, 3, 4)
These subroutines solve the system Ax = b for
x, where A is a general matrix and x and
b are vectors. Using the iopt argument, they can also
solve the real system
ATx = b or the complex
system AHx = b for
x. These subroutines use the results of the factorization of matrix
A, produced by a preceding call to SGEF/SGEFCD, DGEF/DGEFP/DGEFCD,
CGEF, or ZGEF, respectively.
| A, b, x | Subroutine |
| Short-precision real | SGES |
| Long-precision real | DGES |
| Short-precision complex | CGES |
| Long-precision complex | ZGES |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGEF/SGEFCD, DGEF/DGEFP/DGEFCD, CGEF, and ZGEF, respectively. |
| Fortran | CALL SGES | DGES | CGES | ZGES (a, lda, n, ipvt, bx, iopt) |
| C and C++ | sges | dges | cges | zges (a, lda, n, ipvt, bx, iopt); |
| PL/I | CALL SGES | DGES | CGES | ZGES (a, lda, n, ipvt, bx, iopt); |
Specified as: a one-dimensional array of (at least) length n, containing fullword integers.
If iopt = 0, A is used in the computation.
If iopt = 1, AT is used in SGES and DGES. AH is used in CGES and ZGES.
| Note: | No data should be moved to form AT or AH; that is, the matrix A should always be stored in its untransposed form. |
Specified as: a fullword integer; iopt = 0 or 1.
The system Ax = b is solved for x, where A is a general matrix and x and b are vectors. Using the iopt argument, this subroutine can also solve the real system ATx = b or the complex system AHx = b for x. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SGEF/SGEFCD, DGEF/DGEFP/DGEFCD, CGEF, or ZGEF, respectively. The transformed matrix A consists of the upper triangular matrix U and the multipliers necessary to construct L using ipvt, as defined in "Function". For a description of how A is factored, see SGEF, DGEF, CGEF, and ZGEF--General Matrix Factorization.
If n is 0, no computation is performed. See references [36] and [38].
None
| Note: | If the factorization performed by SGEF, DGEF, CGEF, ZGEF, SGEFCD, DGEFCD, or DGEFP failed because a pivot element is zero, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This part of the example shows how to solve the system Ax = b, where matrix A is the same matrix factored in the "Example 1" for SGEF and DGEF.
A LDA N IPVT BX IOPT
| | | | | |
CALL SGES( A , 9 , 9 , IPVT , BX , 0 )
IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9) BX = (4.0, 5.0, 9.0, 10.0, 11.0, 12.0, 12.0, 12.0, 33.0) A =(same as output A in "Example 1")
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
This part of the example shows how to solve the system ATx = b, where matrix A is the input matrix factored in "Example 1" for SGEF and DGEF. Most of the input is the same in Part 2 as in Part 1.
A LDA N IPVT BX IOPT
| | | | | |
CALL SGES( A , 9 , 9 , IPVT , BX , 1 )
IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9) BX = (6.0, 8.0, 10.0, 12.0, 13.0, 14.0, 15.0, 15.0, 15.0) A =(same as output A in "Example 1")
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
This part of the example shows how to solve the system Ax = b, where matrix A is the same matrix factored in the "Example 2" for CGEF and ZGEF.
A LDA N IPVT BX IOPT
| | | | | |
CALL CGES( A , 4 , 4 , IPVT , BX , 0 )
IPVT = (4, 4, 3, 4)
BX = ((-10.0, 85.0), (-6.0, 61.0), (10.0, 38.0),
(58.0, 168.0))
A =(same as output A in
"Example 1")
BX = ((9.0, 0.0), (5.0, 1.0), (1.0, 6.0), (3.0, 4.0))
This part of the example shows how to solve the system AHx = b, where matrix A is the input matrix factored in "Example 2" for CGEF and ZGEF. Most of the input is the same in Part 2 as in Part 1.
A LDA N IPVT BX IOPT
| | | | | |
CALL CGES( A , 4 , 4 , IPVT , BX , 1 )
IPVT = (4, 4, 3, 4)
BX = ((71.0, 12.0), (61.0, -70.0), (123.0, -34.0),
(68.0, 7.0))
A =(same as output A in
"Example 1")
BX = ((9.0, 0.0), (5.0, 1.0), (1.0, 6.0), (3.0, 4.0))
These subroutines solve the following systems of equations for multiple right-hand sides, where A, X, and B are general matrices. SGESM and DGESM solve one of the following:
CGESM and ZGESM solve one of the following:
These subroutines use the results of the factorization of matrix
A, produced by a preceding call to SGEF/SGEFCD, DGEF/DGEFP/DGEFCD,
CGEF, or ZGEF, respectively.
| A, B, X | Subroutine |
| Short-precision real | SGESM |
| Long-precision real | DGESM |
| Short-precision complex | CGESM |
| Long-precision complex | ZGESM |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGEF/SGEFCD, DGEF/DGEFP/DGEFCD, CGEF, and ZGEF, respectively. |
| Fortran | CALL SGESM | DGESM | CGESM | ZGESM (trans, a, lda, n, ipvt, b, ldb, nrhs) |
| C and C++ | sgesm | dgesm | cgesm | zgesm (trans, a, lda, n, ipvt, b, ldb, nrhs); |
| PL/I | CALL SGESM | DGESM | CGESM | ZGESM (trans, a, lda, n, ipvt, b, ldb, nrhs); |
If transa = 'N', A is used in the computation, resulting in equation 1.
If transa = 'T', AT is used in the computation, resulting in equation 2.
If transa = 'C', AH is used in the computation, resulting in equation 3.
Specified as: a single character. It must be 'N', 'T', or 'C'.
Specified as: a one-dimensional array of (at least) length n, containing fullword integers.
One of the following systems of equations is solved for multiple right-hand sides:
where A, B, and X are general matrices. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SGEF/SGEFCD, DGEF/DGEFP/DGEFCD, CGEF, or ZGEF, respectively. The transformed matrix A consists of the upper triangular matrix U and the multipliers necessary to construct L using ipvt, as defined in "Function". For a description of how A is factored, see SGEF, DGEF, CGEF, and ZGEF--General Matrix Factorization.
If n or nrhs is 0, no computation is performed. See references [36] and [38].
None
| Note: | If the factorization performed by SGEF, DGEF, CGEF, ZGEF, SGEFCD, DGEFCD, or DGEFP failed because a pivot element is zero, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This part of the example shows how to solve the system AX = B for two right-hand sides, where matrix A is the same matrix factored in the "Example 1" for SGEF and DGEF.
TRANS A LDA N IPVT B LDB NRHS
| | | | | | | |
CALL SGESM( 'N' , A , 9 , 9 , IPVT , B , 9 , 2 )
IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9) A =(same as output A in "Example 1")
* *
| 4.0 10.0 |
| 5.0 15.0 |
| 9.0 24.0 |
| 10.0 35.0 |
B = | 11.0 48.0 |
| 12.0 63.0 |
| 12.0 70.0 |
| 12.0 78.0 |
| 33.0 266.0 |
* *
* *
| 1.0 1.0 |
| 1.0 2.0 |
| 1.0 3.0 |
| 1.0 4.0 |
B = | 1.0 5.0 |
| 1.0 6.0 |
| 1.0 7.0 |
| 1.0 8.0 |
| 1.0 9.0 |
* *
This part of the example shows how to solve the system ATX = B for two right-hand sides, where matrix A is the input matrix factored in "Example 1" for SGEF and DGEF.
TRANS A LDA N IPVT B LDB NRHS
| | | | | | | |
CALL SGESM( 'T' , A , 9 , 9 , IPVT , B , 9 , 2 )
IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9) A =(same as output A in "Example 1")
* *
| 6.0 15.0 |
| 8.0 26.0 |
| 10.0 40.0 |
| 12.0 57.0 |
B = | 13.0 76.0 |
| 14.0 97.0 |
| 15.0 120.0 |
| 15.0 125.0 |
| 15.0 129.0 |
* *
* *
| 1.0 1.0 |
| 1.0 2.0 |
| 1.0 3.0 |
| 1.0 4.0 |
B = | 1.0 5.0 |
| 1.0 6.0 |
| 1.0 7.0 |
| 1.0 8.0 |
| 1.0 9.0 |
* *
This part of the example shows how to solve the system AX = B for two right-hand sides, where matrix A is the same matrix factored in the "Example 2" for CGEF and ZGEF.
TRANS A LDA N IPVT B LDB NRHS
| | | | | | | |
CALL CGESM( 'N' , A , 4 , 4 , IPVT , B , 4 , 2 )
IPVT = (4, 4, 3, 4) A =(same as output A in "Example 2")
* *
| (-10.0, 85.0) (-11.0, 53.0) |
B = | (-6.0, 61.0) (-6.0, 54.0) |
| (10.0, 38.0) (2.0, 40.0) |
| (58.0, 168.0) (15.0, 105.0) |
* *
* *
| (9.0, 0.0) (1.0, 1.0) |
B = | (5.0, 1.0) (2.0, 2.0) |
| (1.0, 6.0) (3.0, 3.0) |
| (3.0, 4.0) (4.0, 4.0) |
* *
This part of the example shows how to solve the system ATX = B for two right-hand sides, where matrix A is the input matrix factored in "Example 2" for CGEF and ZGEF.
TRANS A LDA N IPVT B LDB NRHS
| | | | | | | |
CALL CGESM( 'T' , A , 4 , 4 , IPVT , B , 4 , 2 )
IPVT = (4, 4, 3, 4) A =(same as output A in "Example 2")
* *
| (71.0, 12.0) (18.0, 68.0) |
B = | (61.0, -70.0) (-27.0, 71.0) |
| (123.0, -34.0) (-11.0, 97.0) |
| (68.0, 7.0) (28.0, 50.0) |
* *
* *
| (9.0, 0.0) (1.0, 1.0) |
B = | (5.0, 1.0) (2.0, 2.0) |
| (1.0, 6.0) (3.0, 3.0) |
| (3.0, 4.0) (4.0, 4.0) |
* *
This part of the example shows how to solve the system AHX = B for two right-hand sides, where matrix A is the input matrix factored in "Example 2" for CGEF and ZGEF.
TRANS A LDA N IPVT B LDB NRHS
| | | | | | | |
CALL CGESM( 'C' , A , 4 , 4 , IPVT , B , 4 , 2 )
IPVT = (4, 4, 3, 4) A =(same as output A in "Example 2")
* *
| (58.0, -3.0) (45.0, 20.0) |
B = | (68.0, -31.0) (83.0, -20.0) |
| (89.0, -22.0) (98.0, 1.0) |
| (53.0, 15.0) (45.0, 25.0) |
* *
* *
| (1.0, 4.0) (4.0, 5.0) |
B = | (2.0, 3.0) (3.0, 4.0) |
| (3.0, 2.0) (2.0, 3.0) |
| (4.0, 1.0) (1.0, 2.0) |
* *
These subroutines factor general matrix A using Gaussian
elimination with partial pivoting. To solve the system of equations with one
or more right-hand sides, follow the call to these subroutines with one or
more calls to SGETRS, DGETRS CGETRS, or ZGETRS, respectively. To compute the
inverse of matrix A, follow the call to these subroutines with a
call to SGEICD or DGEICD, respectively.
| A | Subroutine |
| Short-precision real | SGETRF |
| Long-precision real | DGETRF |
| Short-precision complex | CGETRF |
| Long-precision complex | ZGETRF |
| Note: | The output from these factorization subroutines should be used only as input to the following subroutines for performing a solve or inverse: SGETRS, DGETRS, CGETRS, ZGETRS, SGEICD or DGEICD respectively. |
| Fortran | CALL SGETRF | DGETRF | CGETRF | ZGETRF (m, n, a, lda, ipvt, info) |
| C and C++ | sgetrf | dgetrf | cgetrf | zgetrf (m, n, a, lda, ipvt, info); |
| PL/I | CALL SGETRF | DGETRF | CGETRF | ZGETRF (m, n, a, lda, ipvt, info); |
If info = 0, the factorization of general matrix A completed successfully.
If info > 0, info is set equal to the first i, where Uii is singular and its inverse could not be computed.
Specified as: a fullword integer; info >= 0.
The matrix A is factored using Gaussian elimination with partial pivoting to compute the LU factorization of A, where:
On output, the transformed matrix A contains U in the upper triangle (if m >= n) or upper trapezoid (if m < n). In its strict lower triangle (if m <= n) or lower trapezoid (if m > n), it contains the multipliers necessary to construct, with the help of ipvt, a matrix L, such that A = LU.
If m or n is 0, no computation is performed and the subroutine returns after doing some parameter checking. See references [36] and [59].
Unable to allocate internal work area.
Matrix A is singular.
This example shows a factorization of a real general matrix A of order 9.
M N A LDA IPVT INFO
| | | | | |
CALL DGETRF( 9 , 9 , A, 9 , IPVT, INFO )
* *
| 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 |
| 1.2 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 |
| 1.4 1.2 1.0 1.2 1.4 1.6 1.8 2.0 2.2 |
| 1.6 1.4 1.2 1.0 1.2 1.4 1.6 1.8 2.0 |
A = | 1.8 1.6 1.4 1.2 1.0 1.2 1.4 1.6 1.8 |
| 2.0 1.8 1.6 1.4 1.2 1.0 1.2 1.4 1.6 |
| 2.2 2.0 1.8 1.6 1.4 1.2 1.0 1.2 1.4 |
| 2.4 2.2 2.0 1.8 1.6 1.4 1.2 1.0 1.2 |
| 2.6 2.4 2.2 2.0 1.8 1.6 1.4 1.2 1.0 |
* *
* *
| 2.6 2.4 2.2 2.0 1.8 1.6 1.4 1.2 1.0 |
| 0.4 0.3 0.6 0.8 1.1 1.4 1.7 1.9 2.2 |
| 0.5 -0.4 0.4 0.8 1.2 1.6 2.0 2.4 2.8 |
| 0.5 -0.3 0.0 0.4 0.8 1.2 1.6 2.0 2.4 |
A = | 0.6 -0.3 0.0 0.0 0.4 0.8 1.2 1.6 2.0 |
| 0.7 -0.2 0.0 0.0 0.0 0.4 0.8 1.2 1.6 |
| 0.8 -0.2 0.0 0.0 0.0 0.0 0.4 0.8 1.2 |
| 0.8 -0.1 0.0 0.0 0.0 0.0 0.0 0.4 0.8 |
| 0.9 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.4 |
* *
IPVT = (9, 9, 9, 9, 9, 9, 9, 9, 9) INFO = 0
This example shows a factorization of a complex general matrix A of order 9.
M N A LDA IPVT INFO
| | | | | |
CALL ZGETRF( 9 , 9 , A, 9 , IPVT, INFO )
* *
| (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) (4.4,-1.0) (4.8,-1.0) (5.2,-1.0) |
| (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) (4.4,-1.0) (4.8,-1.0) |
| (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) (4.4,-1.0) |
| (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) (4.0,-1.0) |
A = | (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) (3.6,-1.0) |
| (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) (3.2,-1.0) |
| (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) (2.8,-1.0) |
| (4.8, 1.0) (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) (2.4,-1.0) |
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) |
* *
* *
| (5.2, 1.0) (4.8, 1.0) (4.4, 1.0) (4.0, 1.0) (3.6, 1.0) (3.2, 1.0) (2.8, 1.0) (2.4, 1.0) (2.0, 1.0) |
| (0.4, 0.1) (0.6,-2.0) (1.1,-1.9) (1.7,-1.9) (2.3,-1.8) (2.8,-1.8) (3.4,-1.7) (3.9,-1.7) (4.5,-1.6) |
| (0.5, 0.1) (0.0,-0.1) (0.6,-1.9) (1.2,-1.8) (1.8,-1.7) (2.5,-1.6) (3.1,-1.5) (3.7,-1.4) (4.3,-1.3) |
| (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) (0.7,-1.9) (1.3,-1.7) (2.0,-1.6) (2.7,-1.5) (3.4,-1.4) (4.0,-1.2) |
A = | (0.6, 0.1) (0.0,-0.1) (-0.1,-0.1) (-0.1, 0.0) (0.7,-1.9) (1.5,-1.7) (2.2,-1.6) (2.9,-1.5) (3.7,-1.3) |
| (0.7, 0.1) (0.0,-0.1) (0.0, 0.0) (-0.1, 0.0) (-0.1, 0.0) (0.8,-1.9) (1.6,-1.8) (2.4,-1.6) (3.2,-1.5) |
| (0.8, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-1.9) (1.7,-1.8) (2.5,-1.8) |
| (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-2.0) (1.7,-1.9) |
| (0.9, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.8,-2.0) |
* *
IPVT = (9, 9, 9, 9, 9, 9, 9, 9, 9) INFO = 0
SGETRS and DGETRS solve one of the following systems of equations for multiple right-hand sides:
CGETRS and ZGETRS solve one of the following systems of equations for multiple right-hand sides:
In the formulas above:
These subroutines use the results of the factorization of matrix
A, produced by a preceding call to SGETRF, DGETRF, CGETRF, or
ZGETRF, respectively.
| A, B | Subroutine |
| Short-precision real | SGETRS |
| Long-precision real | DGETRS |
| Short-precision complex | CGETRS |
| Long-precision complex | ZGETRS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGETRF, DGETRF, CGETRF and ZGETRF, respectively. |
| Fortran | CALL SGETRS | DGETRS | CGETRS | ZGETRS (transa, n, nrhs, a, lda, ipvt, bx, ldb, info) |
| C and C++ | sgetrs | dgetrs | cgetrs | zgetrs (transa, n, nrhs, a, lda, ipvt, bx, ldb, info); |
| PL/I | CALL SGETRS | DGETRS | CGETRS | ZGETRS (transa, n, nrhs, a, lda, ipvt, bx, ldb, info); |
If transa = 'N', A is used in the computation, resulting in solution 1.
If transa = 'T', AT is used in the computation, resulting in solution 2.
If transa = 'C', AH is used in the computation, resulting in solution 3.
Specified as: a single character; transa = 'N', 'T', or 'C'.
Specified as: a one-dimensional array of (at least) length n, containing fullword integers, where 1 <= ipvt(i) <= n.
If info = 0, the solve of general matrix A completed successfully.
If, however, you do not plan to call _GETRS after calling _GETRF, then input arguments m and n in _GETRF do not need to be equal.
One of the following systems of equations is solved for multiple right-hand sides:
where A, B, and X are general matrices. These subroutines uses the results of the factorization of matrix A, produced by a preceding call to SGETRF, DGETRF, CGETRF or ZGETRF, respectively. On input, the transformed matrix A consists of the upper triangular matrix U and the multipliers necessary to construct L using ipvt, as defined in "Function". For details on the factorization, see SGETRF, DGETRF, CGETRF and ZGETRF--General Matrix Factorization.
If n = 0 or nrhs = 0, no computation is performed and the subroutine returns after doing some parameter checking. See references [36] and [59].
None
| Note: | If the factorization performed by SGETRF, DGETRF, CGETRF or ZGETRF failed because a pivot element is zero, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This example shows how to solve the system AX = B, where matrix A is the same matrix factored in the "Example 1" for DGETRF.
TRANSA N NRHS A LDA IPIV BX LDB INFO
| | | | | | | | |
CALL DGETRS('N' , 9 , 5 , A , 9 , IPIV, B , 9 , INFO)
IPVT = (9, 9, 9, 9, 9, 9, 9, 9, 9) A =(same as output A in "Example 1")
* *
| 93.0 186.0 279.0 372.0 465.0 |
| 84.4 168.8 253.2 337.6 422.0 |
| 76.6 153.2 229.8 306.4 383.0 |
| 70.0 140.0 210.0 280.0 350.0 |
B = | 65.0 130.0 195.0 260.0 325.0 |
| 62.0 124.0 186.0 248.0 310.0 |
| 61.4 122.8 184.2 245.6 307.0 |
| 63.6 127.2 190.8 254.4 318.0 |
| 69.0 138.0 207.0 276.0 345.0 |
* *
* *
| 1.0 2.0 3.0 4.0 5.0 |
| 2.0 4.0 6.0 8.0 10.0 |
| 3.0 6.0 9.0 12.0 15.0 |
| 4.0 8.0 12.0 16.0 20.0 |
B = | 5.0 10.0 15.0 20.0 25.0 |
| 6.0 12.0 18.0 24.0 30.0 |
| 7.0 14.0 21.0 28.0 35.0 |
| 8.0 16.0 24.0 32.0 40.0 |
| 9.0 18.0 27.0 36.0 45.0 |
* *
INFO = 0
This example shows how to solve the system AX = b, where matrix A is the same matrix factored in the "Example 2" for ZGETRF.
TRANS N NRHS A LDA IPIV B LDB INFO
| | | | | | | | |
CALL ZGETRS('N' , 9 , 5 , A , 9 , IPIV, B , 9 , INFO)
IPVT = (9, 9, 9, 9, 9, 9, 9, 9, 9) A =(same as output A in "Example 2")
* *
| (193.0,-10.6) (200.0, 21.8) (207.0, 54.2) (214.0, 86.6) (221.0,119.0) |
| (173.8, -9.4) (178.8, 20.2) (183.8, 49.8) (188.8, 79.4) (193.8,109.0) |
| (156.2, -5.4) (159.2, 22.2) (162.2, 49.8) (165.2, 77.4) (168.2,105.0) |
| (141.0, 1.4) (142.0, 27.8) (143.0, 54.2) (144.0, 80.6) (145.0,107.0) |
B = | (129.0, 11.0) (128.0, 37.0) (127.0, 63.0) (126.0, 89.0) (125.0,115.0) |
| (121.0, 23.4) (118.0, 49.8) (115.0, 76.2) (112.0,102.6) (109.0,129.0) |
| (117.8, 38.6) (112.8, 66.2) (107.8, 93.8) (102.8,121.4) (97.8,149.0) |
| (120.2, 56.6) (113.2, 86.2) (106.2,115.8) (99.2,145.4) (92.2,175.0) |
| (129.0, 77.4) (120.0,109.8) (111.0,142.2). (102.0,174.6) (93.0,207.0) |
* *
* *
| (1.0,1.0) (1.0,2.0) (1.0,3.0) (1.0,4.0) (1.0,5.0) |
| (2.0,1.0) (2.0,2.0) (2.0,3.0) (2.0,4.0) (2.0,5.0) |
| (3.0,1.0) (3.0,2.0) (3.0,3.0) (3.0,4.0) (3.0,5.0) |
| (4.0,1.0) (4.0,2.0) (4.0,3.0) (4.0,4.0) (4.0,5.0) |
B = | (5.0,1.0) (5.0,2.0) (5.0,3.0) (5.0,4.0) (5.0,5.0) |
| (6.0,1.0) (6.0,2.0) (6.0,3.0) (6.0,4.0) (6.0,5.0) |
| (7.0,1.0) (7.0,2.0) (7.0,3.0) (7.0,4.0) (7.0,5.0) |
| (8.0,1.0) (8.0,2.0) (8.0,3.0) (8.0,4.0) (8.0,5.0) |
| (9.0,1.0) (9.0,2.0) (9.0,3.0) (9.0,4.0) (9.0,5.0) |
* *
INFO = 0
These subroutines factor general matrix A using Gaussian
elimination. An estimate of the reciprocal of the condition number and the
determinant of matrix A can also be computed. To solve a system of
equations with one or more right-hand sides, follow the call to these
subroutines with one or more calls to SGES/SGESM or DGES/DGESM, respectively.
To compute the inverse of matrix A, follow the call to these
subroutines with a call to SGEICD and DGEICD, respectively.
| A, aux, rcond, det | Subroutine |
| Short-precision real | SGEFCD |
| Long-precision real | DGEFCD |
| Note: | The output from these factorization subroutines should be used only as input to the following subroutines for performing a solve or inverse: SGES/SGESM/SGEICD and DGES/DGESM/DGEICD, respectively. |
| Fortran | CALL SGEFCD | DGEFCD (a, lda, n, ipvt, iopt, rcond, det, aux, naux) |
| C and C++ | sgefcd | dgefcd (a, lda, n, ipvt, iopt, rcond, det, aux, naux); |
| PL/I | CALL SGEFCD | DGEFCD (a, lda, n, ipvt, iopt, rcond, det, aux, naux); |
If iopt = 0, the matrix is factored.
If iopt = 1, the matrix is factored, and the reciprocal of the condition number is computed.
If iopt = 2, the matrix is factored, and the determinant is computed.
If iopt = 3, the matrix is factored, and the reciprocal of the condition number and the determinant are computed.
Specified as: a fullword integer; iopt = 0, 1, 2, or 3.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is is a storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing numbers of the data type indicated in Table 92.
If naux = 0 and error 2015 is unrecoverable, SGEFCD and DGEFCD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux >= n.
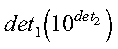
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 92.
Matrix A is factored using Gaussian elimination with partial pivoting to compute the LU factorization of A, where:
The transformed matrix A contains U in the upper triangle. In its strict lower triangle, it contains the multipliers necessary to construct, with the help of ipvt, a matrix L, such that A = LU.
An estimate of the reciprocal of the condition number, rcond, and the determinant, det, can also be computed by this subroutine. The estimate of the condition number uses an enhanced version of the algorithm described in references [63] and [64].
If n is 0, no computation is performed. See reference [36].
These subroutines call SGEF and DGEF, respectively, to perform the factorization. ipvt is an output vector of SGEF and DGEF. It is returned for use by SGES/SGESM and DGES/DGESM, the solve subroutines.
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
Matrix A is singular.
This example shows a factorization of matrix A of order 9. The input is the same as used in SGEF and DGEF. See "Example 1". The reciprocal of the condition number and the determinant of matrix A are also computed. The values used to estimate the reciprocal of the condition number in this example are obtained with the following values:
||A||1 = max(6.0, 8.0, 10.0, 12.0, 13.0, 14.0, 15.0, 15.0, 15.0) = 15.0
Estimate of ||A-1||1 = 1091.87
This estimate is equal to the actual rcond of 5.436(10-5), which is computed by SGEICD and DGEICD. (See "Example 1".) On output, the value in det, |A|, is equal to 336.
A LDA N IPVT IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL DGEFCD( A , 9 , 9 , IPVT , 3 , RCOND , DET , AUX , 9 )
A =(same as input A in "Example 1")
A =(same as output A in "Example 1") IPVT = (3, 4, 5, 6, 7, 8, 9, 8, 9) RCOND = 0.00005436 DET = (3.36, 2.00)
The SPPF and DPPF subroutines factor positive definite symmetric matrix A, stored in lower-packed storage mode, using Gaussian elimination (LDLT) or the Cholesky factorization method. To solve a system of equations with one or more right-hand sides, follow the call to these subroutines with one or more calls to SPPS or DPPS, respectively. To find the inverse of matrix A, follow the call to these subroutines, performing Cholesky factorization, with a call to SPPICD or DPPICD, respectively.
The SPOF, DPOF, CPOF, and ZPOF subroutines factor matrix A stored in upper or lower storage mode, where:
Matrix A is factored using Cholesky factorization,
(LLT or UTU for SPOF
and DPOF and LLH or UHU
for CPOF and ZPOF). To solve the system of equations with one or more
right-hand sides, follow the call to these subroutines with a call to SPOSM,
DPOSM, CPOSM, or ZPOSM. To find the inverse of matrix A, follow the
call to SPOF or DPOF with a call to SPOICD or DPOICD.
| A | Subroutine |
| Short-precision real | SPPF and SPOF |
| Long-precision real | DPPF and DPOF |
| Short-precision complex | CPOF |
| Long-precision complex | ZPOF |
| Note: | The output from SPPF and DPPF should be used only as input to the following subroutines for performing a solve or inverse: SPPS/SPPICD and DPPS/DPPICD, respectively. The output from SPOF, DPOF, CPOF, and ZPOF should be used only as input to the following subroutines for performing a solve or inverse: SPOSM/SPOICD, DPOSM/DPOICD, CPOSM, and ZPOSM, respectively. |
| Fortran | CALL SPPF | DPPF (ap, n, iopt)
CALL SPOF | DPOF | CPOF | ZPOF (uplo, a, lda, n) |
| C and C++ | sppf | dppf (ap, n, iopt);
spof | dpof | cpof | zpof (uplo, a, lda, n); |
| PL/I | CALL SPPF | DPPF (ap, n, iopt);
CALL SPOF | DPOF | CPOF | ZPOF (uplo, a, lda, n); |
If uplo = 'U', A is stored in upper storage mode.
If uplo = 'L', A is stored in lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
Specified as: a one-dimensional array, containing numbers of the data type indicated in Table 93. See "Notes".
If iopt = 0, the array must have at least n(n+1)/2+n elements.
If iopt = 1, the array must have at least n(n+1)/2 elements.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 93.
Specified as: a fullword integer; lda > 0 and lda >= n.
Specified as: a fullword integer; n >= 0.
If iopt = 0, the matrix is factored using the LDLT method.
If iopt = 1, the matrix is factored using Cholesky factorization.
Specified as: a fullword integer; iopt = 0 or 1.
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 93.
If iopt = 0, the array contains n(n+1)/2+n elements.
If iopt = 1, the array contains n(n+1)/2 elements.
Returned as: a two-dimensional array, containing numbers of the data type indicated in Table 93.
The functions for these subroutines are described in the sections below.
If iopt = 0, the positive definite symmetric matrix A, stored in lower-packed storage mode, is factored using Gaussian elimination, where A is expressed as:
where:
If iopt = 1, the positive definite symmetric matrix A is factored using Cholesky factorization, where A is expressed as:
where L is a lower triangular matrix.
If n is 0, no computation is performed. See references [36] and [38].
The positive definite matrix A, stored in upper or lower storage mode, is factored using Cholesky factorization, where A is expressed as:
where:
If n is 0, no computation is performed. See references [8], [64], and [36].
Unable to allocate internal work area.
This example shows a factorization of positive definite symmetric matrix A of order 9, stored in lower-packed storage mode, where on input matrix A is:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 7.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 |
* *
On output, all elements of this matrix A are 1.0.
| Note: | The AP arrays are formatted in a triangular arrangement for readability; however, they are stored in lower-packed storage mode. |
AP N IOPT
| | |
CALL SPPF( AP, 9, 0 )
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0,
3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0,
4.0, 4.0, 4.0, 4.0, 4.0, 4.0,
5.0, 5.0, 5.0, 5.0, 5.0,
6.0, 6.0, 6.0, 6.0,
7.0, 7.0, 7.0,
8.0, 8.0,
9.0,
. , . , . , . , . , . , . , . , . )
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0,
1.0, 1.0,
1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
This example shows a factorization of the same positive definite symmetric matrix A of order 9 used in Example 1, stored in lower-packed storage mode.
| Note: | The AP arrays are formatted in a triangular arrangement for readability; however, they are stored in lower-packed storage mode. |
AP N IOPT
| | |
CALL SPPF( AP, 9, 1 )
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0,
3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0,
4.0, 4.0, 4.0, 4.0, 4.0, 4.0,
5.0, 5.0, 5.0, 5.0, 5.0,
6.0, 6.0, 6.0, 6.0,
7.0, 7.0, 7.0,
8.0, 8.0,
9.0)
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0,
1.0, 1.0,
1.0)
This example shows a factorization of the same positive definite symmetric matrix A of order 9 used in Example 1, but stored in lower storage mode.
UPLO A LDA N
| | | |
CALL SPOF( 'L' , A , 9 , 9 )
* *
| 1.0 . . . . . . . . |
| 1.0 2.0 . . . . . . . |
| 1.0 2.0 3.0 . . . . . . |
| 1.0 2.0 3.0 4.0 . . . . . |
A = | 1.0 2.0 3.0 4.0 5.0 . . . . |
| 1.0 2.0 3.0 4.0 5.0 6.0 . . . |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 . . |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 . |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 |
* *
* *
| 1.0 . . . . . . . . |
| 1.0 1.0 . . . . . . . |
| 1.0 1.0 1.0 . . . . . . |
| 1.0 1.0 1.0 1.0 . . . . . |
A = | 1.0 1.0 1.0 1.0 1.0 . . . . |
| 1.0 1.0 1.0 1.0 1.0 1.0 . . . |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . . |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
* *
This example shows a factorization of the same positive definite symmetric matrix A of order 9 used in Example 1, but stored in upper storage mode.
UPLO A LDA N
| | | |
CALL SPOF( 'U' , A , 9 , 9 )
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| . . 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| . . . 4.0 4.0 4.0 4.0 4.0 4.0 |
A = | . . . . 5.0 5.0 5.0 5.0 5.0 |
| . . . . . 6.0 6.0 6.0 6.0 |
| . . . . . . 7.0 7.0 7.0 |
| . . . . . . . 8.0 8.0 |
| . . . . . . . . 9.0 |
* *
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . . 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . . . 1.0 1.0 1.0 1.0 1.0 1.0 |
A = | . . . . 1.0 1.0 1.0 1.0 1.0 |
| . . . . . 1.0 1.0 1.0 1.0 |
| . . . . . . 1.0 1.0 1.0 |
| . . . . . . . 1.0 1.0 |
| . . . . . . . . 1.0 |
* *
This example shows a factorization of positive definite complex Hermitian matrix A of order 3, stored in lower storage mode, where on input matrix A is:
* *
| (25.0, 0.0) (-5.0, -5.0) (10.0, 5.0) |
| (-5.0, 5.0) (51.0, 0.0) (4.0, -6.0) |
| (10.0, -5.0) (4.0, 6.0) (71.0, 0.0) |
* *
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, they are set to zero. |
UPLO A LDA N
| | | |
CALL CPOF( 'L' , A , 3 , 3 )
* *
| (25.0, . ) . . |
A = | (-5.0, 5.0) (51.0, . ) . |
| (10.0, -5.0) (4.0, 6.0) (71.0, . ) |
* *
* *
| (5.0, 0.0) . . |
A = | (-1.0, 1.0) (7.0, 0.0) . |
| (2.0, -1.0) (1.0, 1.0) (8.0, 0.0) |
* *
This example shows a factorization of positive definite complex Hermitian matrix A of order 3, stored in upper storage mode, where on input matrix A is:
* *
| (9.0, 0.0) (3.0, 3.0) (3.0, -3.0) |
| (3.0, -3.0) (18.0, 0.0) (8.0, -6.0) |
| (3.0, 3.0) (8.0, 6.0) (43.0, 0.0) |
* *
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, they are set to zero. |
UPLO A LDA N
| | | |
CALL CPOF( 'U' , A , 3 , 3 )
* *
| (9.0, . ) (3.0,3.0) (3.0,-3.0) |
A = | . (18.0, . ) (8.0,-6.0) |
| . . (43.0, . ) |
* *
* *
| (3.0, 0.0) (1.0, 1.0) (1.0, -1.0) |
A = | . (4.0, 0.0) (2.0, -1.0) |
| . . (6.0, 0.0) |
* *
These subroutines solve the system Ax = b for
x, where A is a positive definite symmetric matrix, and
x and b are vectors. The subroutines use the results of
the factorization of matrix A, produced by a preceding call to
SPPF/SPPFCD or DPPF/DPPFP/DPPFCD, respectively.
| A, b, x | Subroutine |
| Short-precision real | SPPS |
| Long-precision real | DPPS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SPPF/SPPFCD and DPPF/DPPFP/DPPFCD, respectively. |
| Fortran | CALL SPPS | DPPS (ap, n, bx, iopt) |
| C and C++ | spps | dpps (ap, n, bx, iopt); |
| PL/I | CALL SPPS | DPPS (ap, n, bx, iopt); |
If iopt = 0, the array must contain n(n+1)/2+n elements.
If iopt = 1, the array must contain n(n+1)/2 elements.
If iopt = 0, the matrix was factored using the LDLT method.
If iopt = 1, the matrix was factored using Cholesky factorization.
Specified as: a fullword integer; iopt = 0 or 1.
The system Ax = b is solved for x, where A is a positive definite symmetric matrix, stored in lower-packed storage mode in array AP, and x and b are vectors. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SPPF/SPPFCD or DPPF/DPPFP/DPPFCD, respectively.
If n is 0, no computation is performed. See references [36] and [38].
None
| Note: | If a call to SPPF, DPPF, SPPFCD, DPPFCD, or DPPFP resulted in a nonpositive definite matrix, error 2104 or 2115, SPPS or DPPS results may be unpredictable or numerically unstable. |
This example shows how to solve the system Ax = b, where matrix A is the same matrix factored in the "Example 1" for SPPF and DPPF.
AP N BX IOPT
| | | |
CALL SPPS ( AP , 9 , BX , 0 )
AP =(same as output AP in "Example 1" for SPPF and DPPF) BX = (9.0, 17.0, 24.0, 30.0, 35.0, 39.0, 42.0, 44.0, 45.0)
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
This example shows how to solve the same system as in Example 1, where matrix A is the same matrix factored in the "Example 2" for SPPF and DPPF.
AP N BX IOPT
| | | |
CALL SPPS( AP , 9 , BX , 1 )
AP =(same as output AP in "Example 2" for SPPF and DPPF) BX = (9.0, 17.0, 24.0, 30.0, 35.0, 39.0, 42.0, 44.0, 45.0)
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
These subroutines solve the system AX = B for X, using multiple right-hand sides, where X and B are general matrices and:
These subroutines use the results of the factorization of matrix
A, produced by a preceding call to SPOF/SPOFCD, DPOF/DPOFCD, CPOF,
or ZPOF, respectively.
| A, B, X | Subroutine |
| Short-precision real | SPOSM |
| Long-precision real | DPOSM |
| Short-precision complex | CPOSM |
| Long-precision complex | ZPOSM |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SPOF/SPOFCD, DPOF/DPOFCD, CPOF, and ZPOF, respectively. |
| Fortran | CALL SPOSM | DPOSM | CPOSM | ZPOSM (uplo, a, lda, n, b, ldb, nrhs) |
| C and C++ | sposm | dposm | cposm | zposm (uplo, a, lda, n, b, ldb, nrhs); |
| PL/I | CALL SPOSM | DPOSM | CPOSM | ZPOSM (uplo, a, lda, n, b, ldb, nrhs); |
If uplo = 'U', A is stored in upper storage mode.
If uplo = 'L', A is stored in lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
The system AX = B is solved for X, using multiple right-hand sides, where X and B are general matrices, and A is a positive definite symmetric matrix for SPOSM and DPOSM and a positive definite complex Hermitian matrix for CPOSM and ZPOSM. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SPOF/SPOFCD, DPOF/DPOFCD, CPOF, or ZPOF, respectively. For a description of how A is factored, see SPPF, DPPF, SPOF, DPOF, CPOF, and ZPOF--Positive Definite Real Symmetric or Complex Hermitian Matrix Factorization.
If n or nrhs is 0, no computation is performed. See references [8] and [36].
None
| Note: | If the factorization performed by SPOF, DPOF, CPOF, ZPOF, SPOFCD, or DPOFCD failed because matrix A was not positive definite, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This example shows how to solve the system AX = B for two right-hand sides, where matrix A is the same matrix factored in the "Example 3" for SPOF.
UPLO A LDA N B LDB NRHS
| | | | | | |
CALL SPOSM( 'L' , A , 9 , 9 , B , 9 , 2 )
A =(same as output A in "Example 3")
* *
| 9.0 45.0 |
| 17.0 89.0 |
| 24.0 131.0 |
| 30.0 170.0 |
B = | 35.0 205.0 |
| 39.0 235.0 |
| 42.0 259.0 |
| 44.0 276.0 |
| 45.0 285.0 |
* *
* *
| 1.0 1.0 |
| 1.0 2.0 |
| 1.0 3.0 |
| 1.0 4.0 |
B = | 1.0 5.0 |
| 1.0 6.0 |
| 1.0 7.0 |
| 1.0 8.0 |
| 1.0 9.0 |
* *
This example shows how to solve the system ATX = B for two right-hand sides, where matrix A is the input matrix factored in "Example 4" for SPOF.
UPLO A LDA N B LDB NRHS
| | | | | | |
CALL SPOSM( 'U' , A , 9 , 9 , B , 9 , 2 )
A =(same as output A in "Example 4")
* *
| 9.0 45.0 |
| 17.0 89.0 |
| 24.0 131.0 |
| 30.0 170.0 |
B = | 35.0 205.0 |
| 39.0 235.0 |
| 42.0 259.0 |
| 44.0 276.0 |
| 45.0 285.0 |
* *
* *
| 1.0 1.0 |
| 1.0 2.0 |
| 1.0 3.0 |
| 1.0 4.0 |
B = | 1.0 5.0 |
| 1.0 6.0 |
| 1.0 7.0 |
| 1.0 8.0 |
| 1.0 9.0 |
* *
This example shows how to solve the system AX = B for two right-hand sides, where matrix A is the same matrix factored in the "Example 5" for CPOF.
UPLO A LDA N B LDB NRHS
| | | | | | |
CALL CPOSM( 'L' , A , 3 , 3 , B , 3 , 2 )
A =(same as output A in "Example 5")
* *
| (60.0, -55.0) (70.0, 10.0) |
B = | (34.0, 58.0) (-51.0, 110.0) |
| (13.0, -152.0) (75.0, 63.0) |
* *
* *
| (2.0, -1.0) (2.0, 0.0) |
B = | (1.0, 1.0) (-1.0, 2.0) |
| (0.0, -2.0) (1.0, 1.0) |
* *
This example shows how to solve the system AX = B for two right-hand sides, where matrix A is the input matrix factored in "Example 6" for CPOF.
UPLO A LDA N B LDB NRHS
| | | | | | |
CALL CPOSM( 'U' , A , 3 , 3 , B , 3 , 2 )
A =(same as output A in "Example 6")
* *
| (33.0, -18.0) (15.0, -3.0) |
B = | (45.0, -45.0) (8.0, -2.0) |
| (152.0, 1.0) (43.0, -29.0) |
* *
* *
| (2.0, -1.0) (2.0, 0.0) |
B = | (1.0, -1.0) (0.0, 1.0) |
| (3.0, 0.0) (1.0, -1.0) |
* *
The SPPFCD and DPPFCD subroutines factor positive definite symmetric matrix A, stored in lower-packed storage mode, using Gaussian elimination (LDLT). The reciprocal of the condition number and the determinant of matrix A can also be computed. To solve the system of equations with one or more right-hand sides, follow the call to these subroutines with one or more calls to SPPS or DPPS, respectively.
The SPOFCD and DPOFCD subroutines factor positive definite symmetric matrix
A, stored in upper or lower storage mode, using Cholesky
factorization (LLT or
UTU). The reciprocal of the condition number
and the determinant of matrix A can also be computed. To solve the
system of equations with one or more right-hand sides, follow the call to
these subroutines with a call to SPOSM or DPOSM, respectively. To find the
inverse of matrix A, follow the call to these subroutines with a
call to SPOICD or DPOICD, respectively.
| A, aux, rcond, det | Subroutine |
| Short-precision real | SPPFCD and SPOFCD |
| Long-precision real | DPPFCD and DPOFCD |
| Note: | The output factorization from SPPFCD and DPPFCD should be used only as input to the solve subroutines SPPS and DPPS, respectively. The output from SPOFCD and DPOFCD should be used only as input to the following subroutines for performing a solve or inverse: SPOSM/SPOICD and DPOSM/DPOICD, respectively. |
| Fortran | CALL SPPFCD | DPPFCD (ap, n, iopt,
rcond, det, aux, naux)
CALL SPOFCD | DPOFCD (uplo, a, lda, n, iopt, rcond, det, aux, naux) |
| C and C++ | sppfcd | dppfcd (ap, n, iopt, rcond,
det, aux, naux);
spofcd | dpofcd (uplo, a, lda, n, iopt, rcond, det, aux, naux); |
| PL/I | CALL SPPFCD | DPPFCD (ap, n, iopt,
rcond, det, aux, naux);
CALL SPOFCD | DPOFCD (uplo, a, lda, n, iopt, rcond, det, aux, naux); |
If uplo = 'U', A is stored in upper storage mode.
If uplo = 'L', A is stored in lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
For SPPFCD and DPPFCD, n >= 0.
For SPOFCD and DPOFCD, 0 <= n <= lda.
If iopt = 0, the matrix is factored.
If iopt = 1, the matrix is factored, and the reciprocal of the condition number is computed.
If iopt = 2, the matrix is factored, and the determinant is computed.
If iopt = 3, the matrix is factored and the reciprocal of the condition number and the determinant are computed.
Specified as: a fullword integer; iopt = 0, 1, 2, or 3.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, is the storage work area used by these subroutines. Its size is specified by naux. Specified as: an area of storage, containing numbers of the data type indicated in Table 96.
If naux = 0 and error 2015 is unrecoverable, SPPFCD, DPPFCD, SPOFCD, and DPOFCD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux >= n.
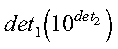
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 96.
The functions for these subroutines are described in the sections below.
The positive definite symmetric matrix A, stored in lower-packed storage mode, is factored using Gaussian elimination, where A is expressed as:
.
where:
An estimate of the reciprocal of the condition number, rcond, and the determinant, det, can also be computed by this subroutine. The estimate of the condition number uses an enhanced version of the algorithm described in references [63] and [64].
If n is 0, no computation is performed. See references [36] and [38].
These subroutines call SPPF and DPPF, respectively, to perform the factorization using Gaussian elimination (LDLT). If you want to use the Cholesky factorization method, you must call SPPF and DPPF directly.
The positive definite symmetric matrix A, stored in upper or lower storage mode, is factored using Cholesky factorization, where A is expressed as:
where:
If specified, the estimate of the reciprocal of the condition number and the determinant can also be computed. The estimate of the condition number uses an enhanced version of the algorithm described in references [63] and [64].
If n is 0, no computation is performed. See references [8] and [36].
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
This example computes the factorization, reciprocal of the condition number, and determinant of matrix A. The input is the same as used in "Example 1" for SPPF.
The values used to estimate the reciprocal of the condition number are obtained with the following values:
On output, the value in det, |A|, is equal to 1.
AP N IOPT RCOND DET AUX NAUX
| | | | | | |
CALL DPPFCD( AP , 9 , 3 , RCOND , DET , AUX , 9 )
AP =(same as input AP in "Example 1")
AP =(same as output AP in "Example 1") RCOND = 0.0055555 DET = (1.0, 0.0)
This example computes the factorization, reciprocal of the condition number, and determinant of matrix A. The input is the same as used in "Example 3" for SPOF.
The values used to estimate the reciprocal of the condition number are obtained with the following values:
On output, the value in det, |A|, is equal to 1.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOFCD( 'L', A , 9 , 9 , 3 , RCOND , DET , AUX , 9 )
A =(same as input A in "Example 3")
A =(same as output A in "Example 3") RCOND = 0.0055555 DET = (1.0, 0.0)
This example computes the factorization, reciprocal of the condition number, and determinant of matrix A. The input is the same as used in "Example 4" for SPOF.
The values used to estimate the reciprocal of the condition number are obtained with the following values:
On output, the value in det, |A|, is equal to 1.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOFCD( 'U', A , 9 , 9 , 3 , RCOND , DET , AUX , 9 )
A =(same as input A in "Example 4")
A =(same as output A in "Example 4") RCOND = 0.0055555 DET = (1.0, 0.0)
These subroutines find the inverse, the reciprocal of the condition number,
and the determinant of matrix A.
| A, aux, rcond, det | Subroutine |
| Short-precision real | SGEICD |
| Long-precision real | DGEICD |
| Note: | If you call these subroutines with iopt = 0, 1, 2, or 3 the input must be the output from the factorization subroutines SGEF/SGEFCD/SGETRF or DGEF/DGEFCD/DGEFP/DGETRF, respectively. |
| Fortran | CALL SGEICD | DGEICD (a, lda, n, iopt, rcond, det, aux, naux) |
| C and C++ | sgeicd | dgeicd (a, lda, n, iopt, rcond, det, aux, naux); |
| PL/I | CALL SGEICD | DGEICD (a, lda, n, iopt, rcond, det, aux, naux); |
If iopt = 0, 1, 2, or 3, it is matrix A of order n, whose inverse, reciprocal of condition number, and determinant are computed.
If iopt = 4, it is the transformed matrix A of order n, resulting from the factorization performed in a previous call to SGEF/SGEFCD or DGEF/DGEFCD/DGEFP, respectively, whose inverse is computed.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 97.
If iopt = 0, the inverse is computed for matrix A.
If iopt = 1, the inverse and the reciprocal of the condition number are computed for matrix A.
If iopt = 2, the inverse and the determinant are computed for matrix A.
If iopt = 3, the inverse, the reciprocal of the condition number, and the determinant are computed for matrix A.
If iopt = 4, the inverse is computed using the factored matrix A.
Specified as: a fullword integer; iopt = 0, 1, 2, 3, 4.
If iopt = 0, 1, 2, or 3, then if naux = 0 and error 2015 is unrecoverable, aux is ignored. Otherwise, it is the storage work area used by this subroutine.
If iopt = 4, aux has the following meaning:
Specified as: an area of storage, containing numbers of the data type indicated in Table 97.
If iopt <> 4, then if naux = 0 and error 2015 is unrecoverable, SGEICD and DGEICD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise naux must have the following value:
For the RS/6000 POWER or PowerPC processors, naux >= 100n.
For the RS/6000 POWER2 processors, naux >= 200n.
| Note: | naux values specified for releases prior to ESSL Version 2 Release 2 will still work, but you may not achieve optimal performance. |
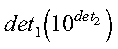
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 97.
| For _GEF_ | For _GEICD |
|---|---|
| Input arguments n and lda | Input arguments n and lda |
| Output arguments a and ipvt | Input arguments a and aux |
The inverse, the reciprocal of the condition number, and the determinant of a general square matrix A are computed using partial pivoting to preserve accuracy, where:
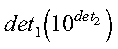
The iopt argument is used to determine the combination of output items produced by this subroutine: the inverse, the reciprocal of the condition number, and the determinant.
If n is 0, no computation is performed. See references [36], [38], and [44].
If iopt = 0, 1, 2, or 3, then error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
Matrix A is singular or nearly singular.
This example computes the inverse, the reciprocal of the condition number, and the determinant of matrix A. The values used to compute the reciprocal of the condition number in this example are obtained with the following values:
On output, the value in det, |A|, is equal to 336.
A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | |
CALL DGEICD( A , 9 , 9 , 3 , RCOND , DET , AUX , 293 )
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 |
| 4.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 0.0 5.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 |
A = | 0.0 0.0 6.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 0.0 0.0 0.0 7.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 8.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 9.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 10.0 11.0 12.0 |
* *
* *
| 0.333 -0.667 0.333 0.000 0.000 0.000 0.042 -0.042 0.000 |
| 56.833 -52.167 -1.167 -0.500 -0.500 -0.357 6.836 -0.479 -0.500 |
| -55.167 51.833 0.833 0.500 0.500 0.214 -6.735 0.521 0.500 |
| -1.000 1.000 0.000 0.000 0.000 0.143 -0.143 0.000 0.000 |
A = | -1.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 |
| -1.000 1.000 0.000 0.000 0.000 0.000 -0.125 0.125 0.000 |
| -226.000 206.000 5.000 3.000 2.000 1.429 -27.179 1.750 2.000 |
| 560.000 -520.000 -10.000 -6.000 -4.000 -2.857 67.857 -5.000 -5.000 |
| -325.000 305.000 5.000 3.000 2.000 1.429 -39.554 3.125 3.000 |
* *
RCOND = 0.00005436
DET = (3.36, 2.00)
This example computes the inverse of matrix A, where iopt = 4 and matrix A is the transformed matrix factored in "Example 1" by SGEF. The input contents of AUX, shown here, is the same as the output contents of IPVT in that example.
A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | |
CALL SGEICD( A , 9 , 9 , 4 , RCOND , DET , AUX , 300 )
A =(same as output A in "Example 1") AUX = (3, 4, 5, 6, 7, 8, 9, 8, 9)
* *
| 0.333 -0.667 0.333 0.000 0.000 0.000 0.042 -0.042 0.000 |
| 56.833 -52.167 -1.167 -0.500 -0.500 -0.357 6.836 -0.479 -0.500 |
| -55.167 51.833 0.833 0.500 0.500 0.214 -6.735 0.521 0.500 |
| -1.000 1.000 0.000 0.000 0.000 0.143 -0.143 0.000 0.000 |
A = | -1.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 |
| -1.000 1.000 0.000 0.000 0.000 0.000 -0.125 0.125 0.000 |
| -226.000 206.000 5.000 3.000 2.000 1.429 -27.179 1.750 2.000 |
| 560.000 -520.000 -10.000 -6.000 -4.000 -2.857 67.857 -5.000 -5.000 |
| -325.000 305.000 5.000 3.000 2.000 1.429 -39.554 3.125 3.000 |
* *
These subroutines find the inverse, the reciprocal of the condition number, and the determinant of positive definite symmetric matrix A using Cholesky factorization, where:
| A, aux, rcond, det | Subroutine |
| Short-precision real | SPPICD and SPOICD |
| Long-precision real | DPPICD and DPOICD |
| Note: | If you call these subroutines with iopt = 4, the input must be the output from the factorization subroutines SPPF, DPPF, SPOF/SPOFCD, or DPOF/DPOFCD, respectively, where Cholesky factorization was performed. |
| Fortran | CALL SPPICD | DPPICD (ap, n, iopt,
rcond, det, aux, naux)
CALL SPOICD | DPOICD (uplo, a, lda, n, iopt, rcond, det, aux, naux) |
| C and C++ | sppicd | dppicd (ap, n, iopt, rcond,
det, aux, naux);
spoicd | dpoicd (uplo, a, lda, n, iopt, rcond, det, aux, naux); |
| PL/I | CALL SPPICD | DPPICD (ap, n, iopt,
rcond, det, aux, naux);
CALL SPOICD | DPOICD (uplo, a, lda, n, iopt, rcond, det, aux, naux); |
If uplo = 'U', A is stored in upper storage mode.
If uplo = 'L', A is stored in lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
If iopt = 0, 1, 2, or 3, then AP contains the positive definite real symmetric matrix A, whose inverse, condition number reciprocal, and determinant are computed, where matrix A is stored in lower-packed storage mode.
If iopt = 4, then AP contains the transformed matrix A of order n, resulting from the Cholesky factorization performed in a previous call to SPPF or DPPF, respectively, whose inverse is computed.
Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 98.
If iopt = 0, 1, 2, or 3, it is the positive definite real symmetric matrix A, whose inverse, condition number reciprocal, and determinant are computed, where matrix A is stored in upper or lower storage mode.
If iopt = 4, it is the transformed matrix A of order n, containing results of the factorization from a previous call to SPOF/SPOFCD or DPOF/DPOFCD, respectively, whose inverse is computed.
Specified as: an n by (at least) n array, containing numbers of the data type indicated in Table 98.
If iopt = 0, the inverse is computed for matrix A.
If iopt = 1, the inverse and the reciprocal of the condition number are computed for matrix A.
If iopt = 2, the inverse and the determinant are computed for matrix A.
If iopt = 3, the inverse, the reciprocal of the condition number, and the determinant are computed for matrix A.
If iopt = 4, the inverse is computed for the (Cholesky) factored matrix A.
Specified as: a fullword integer; iopt = 0, 1, 2, 3, or 4.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux. Specified as: an area of storage, containing numbers of the data type indicated in Table 98.
If naux = 0 and error 2015 is unrecoverable, SPPICD, DPPICD, SPOICD, AND DPOICD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux >= n.
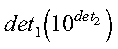
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 98.
These subroutines find the inverse, the reciprocal of the condition number, and the determinant of positive definite symmetric matrix A using Cholesky factorization, where:
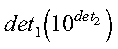
The iopt argument is used to determine the combination of output items produced by this subroutine: the inverse, the reciprocal of the condition number, and the determinant.
If n is 0, no computation is performed. See references [36], [38], and [44].
Matrix A is not positive definite.
For iopt = 4 for SPPICD and DPPICD, if the Cholesky factorization performed by SPPF or DPPF, respectively, failed due to a nonpositive definite matrix A, the results from STPI or DTPI, respectively, are unpredictable, and a computational error message may be issued.
For iopt = 4 for SPOICD and DPOICD, if the factorization performed by SPOF/SPOFCD or DPOF/DPOFCD, respectively, failed due to a nonpositive definite matrix A, the results from STRI or DTRI, respectively, are unpredictable, and a computational error message may be issued.
This example uses SPPICD to compute the inverse, reciprocal of the condition number, and determinant of matrix A. Where A is:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 7.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 |
* *
The values used to compute the reciprocal of the condition number in this example are obtained with the following values:
On output, the value in det, |A|, is equal to 1, and RCOND = 1/180.
| Note: | The AP arrays are formatted in a triangular arrangement for readability; however, they are stored in lower-packed storage mode. |
AP N IOPT RCOND DET AUX NAUX
| | | | | | |
CALL SPPICD( AP , 9 , 3 , RCOND , DET , AUX , 9 )
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0,
3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0,
4.0, 4.0, 4.0, 4.0, 4.0, 4.0,
5.0, 5.0, 5.0, 5.0, 5.0,
6.0, 6.0, 6.0, 6.0,
7.0, 7.0, 7.0,
8.0, 8.0,
9.0)
AP = (2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0,
2.0, -1.0, 0.0,
2.0, -1.0,
1.0)
RCOND = 0.005556
DET = (1.0, 0.0)
This example uses SPPICD to compute the inverse of matrix A, where iopt = 4, and matrix A is the transformed matrix factored in "Example 1" by SPPF.
| Note: | The AP arrays are formatted in a triangular arrangement for readability; however, they are stored in lower-packed storage mode. |
AP N IOPT RCOND DET AUX NAUX
| | | | | | |
CALL SPPICD(AP , 9 , 4 , RCOND , DET , AUX , 9)
AP =(same as output AP in "Example 2" for SPPF)
AP = (2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0,
2.0, -1.0, 0.0,
2.0, -1.0,
1.0)
This example uses SPOICD to compute the inverse, reciprocal of the condition number, and determinant of the same matrix A used in Example 1; however, matrix A is stored in upper storage mode in this example.
The values used to compute the reciprocal of the condition number in this example are obtained with the following values:
On output, the value in det, |A|, is equal to 1, and RCOND = 1/180.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOICD( 'U' , A , 9 , 9 , 3 , RCOND , DET , AUX , 9 )
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| . . 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| . . . 4.0 4.0 4.0 4.0 4.0 4.0 |
A = | . . . . 5.0 5.0 5.0 5.0 5.0 |
| . . . . . 6.0 6.0 6.0 6.0 |
| . . . . . . 7.0 7.0 7.0 |
| . . . . . . . 8.0 8.0 |
| . . . . . . . . 9.0 |
* *
* *
| 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| . . . 2.0 -1.0 0.0 0.0 0.0 0.0 |
A = | . . . . 2.0 -1.0 0.0 0.0 0.0 |
| . . . . . 2.0 -1.0 0.0 0.0 |
| . . . . . . 2.0 -1.0 0.0 |
| . . . . . . . 2.0 -1.0 |
| . . . . . . . . 1.0 |
* *
RCOND = 0.005555556
DET = (1.0, 0.0)
This example uses SPOICD to compute the inverse of matrix A, where iopt = 4, and matrix A is the transformed matrix factored in "Example 1" by SPOF.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOICD( 'U' , A , 9 , 9 , 4 , RCOND , DET , AUX , 9 )
A =(same as output A in "Example 4" for SPOF)
* *
| 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| . . . 2.0 -1.0 0.0 0.0 0.0 0.0 |
A = | . . . . 2.0 -1.0 0.0 0.0 0.0 |
| . . . . . 2.0 -1.0 0.0 0.0 |
| . . . . . . 2.0 -1.0 0.0 |
| . . . . . . . 2.0 -1.0 |
| . . . . . . . . 1.0 |
* *
STRSV, DTRSV, STPSV, and DTPSV perform one of the following solves for a
triangular system of equations with a single right-hand side, using the vector
x and triangular matrix A or its transpose:
| Solution | Equation |
|
|---|---|---|
| 1. x <-- A-1x | Ax = b |
|
| 2. x <-- A-Tx | ATx = b |
|
CTRSV, ZTRSV, CTPSV, and ZTPSV perform one of the following solves for a
triangular system of equations with a single right-hand side, using the vector
x and and triangular matrix A, its transpose, or its
conjugate transpose:
| Solution | Equation |
|
|---|---|---|
| 1. x <-- A-1x | Ax = b |
|
| 2. x <-- A-Tx | ATx = b |
|
| 3. x <-- A-Tx | AHx = b |
|
Matrix A can be either upper or lower triangular, where:
| Note: | The term b used in the systems of equations listed above represents the right-hand side of the system. It is important to note that in these subroutines the right-hand side of the equation is actually provided in the input-output argument x. |
| A, x | Subroutine |
| Short-precision real | STRSV and STPSV |
| Long-precision real | DTRSV and DTPSV |
| Short-precision complex | CTRSV and CTPSV |
| Long-precision complex | ZTRSV and ZTPSV |
| Fortran | CALL STRSV | DTRSV | CTRSV | ZTRSV (uplo, transa,
diag, n, a, lda, x,
incx)
CALL STPSV | DTPSV | CTPSV | ZTPSV (uplo, transa, diag, n, ap, x, incx) |
| C and C++ | strsv | dtrsv | ctrsv | ztrsv (uplo, transa,
diag, n, a, lda, x,
incx);
stpsv | dtpsv | ctpsv | ztpsv (uplo, transa, diag, n, ap, x, incx); |
| PL/I | CALL STRSV | DTRSV | CTRSV | ZTRSV (uplo, transa,
diag, n, a, lda, x,
incx);
CALL STPSV | DTPSV | CTPSV | ZTPSV (uplo, transa, diag, n, ap, x, incx); |
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If transa = 'N', A is used, resulting in solution 1.
If transa = 'T', AT is used, resulting in solution 2.
If transa = 'C', AH is used, resulting in solution 3.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
These subroutines solve a triangular system of equations with a single right-hand side. The solution x may be any of the following, where triangular matrix A, its transpose, or its conjugate transpose is used, and where A can be either upper- or lower-triangular:
where:
If n is 0, no computation is performed. See references [32], [36], and [38].
None
This example shows the solution x <-- A-1x. Matrix A is a real 4 by 4 lower unit triangular matrix, stored in lower-triangular storage mode. Vector x is a vector of length 4.
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL STRSV( 'L' , 'N' , 'U' , 4 , A , 4 , X , 1 )
* *
| . . . . |
| 1.0 . . . |
A = | 2.0 3.0 . . |
| 3.0 4.0 3.0 . |
* *
X = (1.0, 3.0, 11.0, 24.0)
X = (1.0, 2.0, 3.0, 4.0)
This example shows the solution x <-- A-Tx. Matrix A is a real 4 by 4 upper nonunit triangular matrix, stored in upper-triangular storage mode. Vector x is a vector of length 4.
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL STRSV( 'U' , 'T' , 'N' , 4 , A , 4 , X , 1 )
* *
| 1.0 2.0 3.0 2.0 |
A = | . 2.0 2.0 5.0 |
| . . 3.0 3.0 |
| . . . 1.0 |
* *
X = (5.0, 18.0, 32.0, 41.0)
X = (5.0, 4.0, 3.0, 2.0)
This example shows the solution x <-- A-Tx. Matrix A is a complex 4 by 4 upper unit triangular matrix, stored in upper-triangular storage mode. Vector x is a vector of length 4.
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of (1.0, 0.0) for the diagonal elements. |
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL CTRSV( 'U' , 'C' , 'U' , 4 , A , 4 , X , 1 )
* *
| . (2.0, 2.0) (3.0, 3.0) (2.0, 2.0) |
A = | . . (2.0, 2.0) (5.0, 5.0) |
| . . . (3.0, 3.0) |
| . . . . |
* *
X = ((5.0, 5.0), (24.0, 4.0), (49.0, 3.0), (80.0, 2.0))
X = ((5.0, 5.0), (4.0, 4.0), (3.0, 3.0), (2.0, 2.0))
This example shows the solution x <-- A-1x. Matrix A is a real 4 by 4 lower unit triangular matrix, stored in lower-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 . . . |
| 1.0 1.0 . . |
| 2.0 3.0 1.0 . |
| 3.0 4.0 3.0 1.0 |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL STPSV( 'L' , 'N' , 'U' , 4 , AP , X , 1 )
AP = ( . , 1.0, 2.0, 3.0, . , 3.0, 4.0, . , 3.0, . )
X = (1.0, 3.0, 11.0, 24.0)
X = (1.0, 2.0, 3.0, 4.0)
This example shows the solution x <-- A-Tx. Matrix A is a real 4 by 4 upper nonunit triangular matrix, stored in upper-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 2.0 3.0 2.0 |
| . 2.0 2.0 5.0 |
| . . 3.0 3.0 |
| . . . 1.0 |
* *
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL STPSV( 'U' , 'T' , 'N' , 4 , AP , X , 1 )
AP = (1.0, 2.0, 2.0, 3.0, 2.0, 3.0, 2.0, 5.0, 3.0, 1.0)
X = (5.0, 18.0, 32.0, 41.0)
X = (5.0, 4.0, 3.0, 2.0)
This example shows the solution x <-- A-Tx. Matrix A is a complex 4 by 4 upper unit triangular matrix, stored in upper-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| (1.0, 0.0) (2.0, 2.0) (3.0, 3.0) (2.0, 2.0) |
| . (1.0, 0.0) (2.0, 2.0) (5.0, 5.0) |
| . . (1.0, 0.0) (3.0, 3.0) |
| . . . (1.0, 0.0) |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of (1.0, 0.0) for the diagonal elements. |
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL CTPSV( 'U' , 'C' , 'U' , 4 , AP , X , 1 )
AP = ( . , (2.0, 2.0), . , (3.0, 3.0), (2.0, 2.0), . ,
(2.0, 2.0), (5.0, 5.0), (3.0, 3.0), . )
X = ((5.0, 5.0), (24.0, 4.0), (49.0, 3.0), (80.0, 2.0))
X = ((5.0, 5.0), (4.0, 4.0), (3.0, 3.0), (2.0, 2.0))
STRSM and DTRSM perform one of the following solves for a triangular system
of equations with multiple right-hand sides, using scalar alpha, rectangular
matrix B, and triangular matrix A or its
transpose:
| Solution | Equation |
|
|---|---|---|
| 1. B <-- alpha(A-1)B | AX = alphaB |
|
| 2. B <-- alpha(A-T)B | ATX = alphaB |
|
| 3. B <-- alphaB(A-1) | XA = alphaB |
|
| 4. B <-- alphaB(A-T) | XAT = alphaB |
|
CTRSM and ZTRSM perform one of the following solves for a triangular system
of equations with multiple right-hand sides, using scalar alpha, rectangular
matrix B, and triangular matrix A, its transpose, or its
conjugate transpose:
| Solution | Equation |
|
|---|---|---|
| 1. B <-- alpha(A-1)B | AX = alphaB |
|
| 2. B <-- alpha(A-T)B | ATX = alphaB |
|
| 3. B <-- alphaB(A-1) | XA = alphaB |
|
| 4. B <-- alphaB(A-T) | XAT = alphaB |
|
| 5. B <-- alpha(A-T)B | AHX = alphaB |
|
| 6. B <-- alphaB(A-T) | XAH = alphaB |
|
| Note: | The term X used in the systems of equations listed above represents the output solution matrix. It is important to note that in these subroutines the solution matrix is actually returned in the input-output argument b. |
| A, B, alpha | Subroutine |
| Short-precision real | STRSM |
| Long-precision real | DTRSM |
| Short-precision complex | CTRSM |
| Long-precision complex | ZTRSM |
| Fortran | CALL STRSM | DTRSM | CTRSM | ZTRSM (side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
| C and C++ | strsm | dtrsm | ctrsm | ztrsm (side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb); |
| PL/I | CALL STRSM | DTRSM | CTRSM | ZTRSM (side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb); |
If side = 'L', A is to the left of B, resulting in solution 1, 2, or 5.
If side = 'R', A is to the right of B, resulting in solution 3, 4, or 6.
Specified as: a single character. It must be 'L' or 'R'.
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If transa = 'N', A is used, resulting in solution 1 or 3.
If transa = 'T', AT is used, resulting in solution 2 or 4.
If transa = 'C', AH is used, resulting in solution 5 or 6.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
If side = 'L', m is the order of triangular matrix A.
Specified as: a fullword integer, where:
If side = 'L', 0 <= m <= lda and m <= ldb.
If side = 'R', 0 <= m <= ldb.
If side = 'R', n is the order of triangular matrix A.
Specified as: a fullword integer; n >= 0, and:
If side = 'R', n <= lda.
If side = 'L', A is order m.
If side = 'R', A is order n.
Specified as: a two-dimensional array, containing numbers of the data type indicated in Table 100, where:
If side = 'L', its size must be lda by (at least) m.
If side = 'R', it size must be lda by (at least) n.
If side = 'L', lda >= m.
If side = 'R', lda >= n.
Returned as: an ldb by (at least) n array, containing numbers of the data type indicated in Table 100.
These subroutines solve a triangular system of equations with multiple right-hand sides. The solution B may be any of the following, where A is a triangular matrix and B is a rectangular matrix:
where:
If n or m is 0, no computation is performed. See references [32] and [36].
Unable to allocate internal work area.
None
| Note: | If the triangular matrix A is singular, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This example shows the solution B <-- alpha(A-1)B, where A is a real 5 by 5 upper triangular matrix that is not unit triangular, and B is a real 5 by 3 rectangular matrix.
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL STRSM( 'L' , 'U' , 'N' , 'N' , 5 , 3 , 1.0 , A , 7 , B , 6 )
* *
| 3.0 -1.0 2.0 2.0 1.0 |
| . -2.0 4.0 -1.0 3.0 |
| . . -3.0 0.0 2.0 |
A = | . . . 4.0 -2.0 |
| . . . . 1.0 |
| . . . . . |
| . . . . . |
* *
* *
| 6.0 10.0 -2.0 |
| -16.0 -1.0 6.0 |
B = | -2.0 1.0 -4.0 |
| 14.0 0.0 -14.0 |
| -1.0 2.0 1.0 |
| . . . |
* *
* *
| 2.0 3.0 1.0 |
| 5.0 5.0 4.0 |
B = | 0.0 1.0 2.0 |
| 3.0 1.0 -3.0 |
| -1.0 2.0 1.0 |
| . . . |
* *
This example shows the solution B <-- alpha(A-T)B, where A is a real 5 by 5 upper triangular matrix that is not unit triangular, and B is a real 5 by 4 rectangular matrix.
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL STRSM( 'L' , 'U' , 'T' , 'N' , 5 , 4 , 1.0 , A , 7 , B , 6 )
* *
| -1.0 -4.0 -2.0 2.0 3.0 |
| . -2.0 2.0 2.0 2.0 |
| . . -3.0 -1.0 4.0 |
A = | . . . 1.0 0.0 |
| . . . . -2.0 |
| . . . . . |
| . . . . . |
* *
* *
| -1.0 -2.0 -3.0 -4.0 |
| 2.0 -2.0 -14.0 -12.0 |
B = | 10.0 5.0 -8.0 -7.0 |
| 14.0 15.0 1.0 8.0 |
| -3.0 4.0 3.0 16.0 |
| . . . . |
* *
* *
| 1.0 2.0 3.0 4.0 |
| 3.0 3.0 -1.0 2.0 |
B = | -2.0 -1.0 0.0 1.0 |
| 4.0 4.0 -3.0 -3.0 |
| 2.0 2.0 2.0 2.0 |
| . . . . |
* *
This example shows the solution B <-- alphaB(A-1), where A is a real 5 by 5 lower triangular matrix that is not unit triangular, and B is a real 3 by 5 rectangular matrix.
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL STRSM( 'R' , 'L' , 'N' , 'N' , 3 , 5 , 1.0 , A , 7 , B , 4 )
* *
| 2.0 . . . . |
| 2.0 3.0 . . . |
| 2.0 1.0 1.0 . . |
A = | 0.0 3.0 0.0 -2.0 . |
| 2.0 4.0 -1.0 2.0 -1.0 |
| . . . . . |
| . . . . . |
* *
* *
| 10.0 4.0 0.0 0.0 1.0 |
B = | 10.0 14.0 -4.0 6.0 -3.0 |
| -8.0 2.0 -5.0 4.0 -2.0 |
| . . . . . |
* *
* *
| 3.0 4.0 -1.0 -1.0 -1.0 |
B = | 2.0 1.0 -1.0 0.0 3.0 |
| -2.0 -1.0 -3.0 0.0 2.0 |
| . . . . . |
* *
This example shows the solution B <-- alphaB(A-1), where A is a real 6 by 6 upper triangular matrix that is unit triangular, and B is a real 1 by 6 rectangular matrix.
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal element. |
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL STRSM( 'R' , 'U' , 'N' , 'U' , 1 , 6 , 1.0 , A , 7 , B , 2 )
* *
| . 2.0 -3.0 1.0 2.0 4.0 |
| . . 0.0 1.0 1.0 -2.0 |
| . . . 4.0 -1.0 1.0 |
A = | . . . . 0.0 -1.0 |
| . . . . . 2.0 |
| . . . . . . |
| . . . . . . |
* *
* *
B = | 1.0 4.0 -2.0 10.0 2.0 -6.0 |
| . . . . . . |
* *
* *
B = | 1.0 2.0 1.0 3.0 -1.0 -2.0 |
| . . . . . . |
* *
This example shows the solution B <-- alphaB(A-1), where A is a complex 5 by 5 lower triangular matrix that is not unit triangular, and B is a complex 3 by 5 rectangular matrix.
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL CTRSM( 'R' , 'L' , 'N' , 'N' , 3 , 5 , ALPHA , A , 7 , B , 4 )
ALPHA = (1.0, 0.0)
* *
| (2.0, -3.0) . . . . |
| (2.0, -4.0) (3.0, -1.0) . . . |
| (2.0, 2.0) (1.0, 2.0) (1.0, 1.0) . . |
A = | (0.0, 0.0) (3.0, -1.0) (0.0, -1.0) (-2.0, 1.0) . |
| (2.0, 2.0) (4.0, 0.0) (-1.0, 2.0) (2.0, -4.0) (-1.0, -4.0) |
| . . . . . |
| . . . . . |
* *
* *
| (22.0, -41.0) (7.0, -26.0) (9.0, 0.0) (-15.0, -3.0) (-15.0, 8.0) |
B = | (29.0, -18.0) (24.0, -10.0) (9.0, 6.0) (-12.0, -24.0) (-19.0, -8.0) |
| (-15.0, 2.0) (-3.0, -21.0) (-2.0, 4.0) (-4.0, -12.0) (-10.0, -6.0) |
| . . . . . |
* *
* *
| (3.0, 0.0) (4.0, 0.0) (-1.0, -2.0) (-1.0, -1.0) (-1.0, -4.0) |
B = | (2.0, -1.0) (1.0, 2.0) (-1.0, -3.0) (0.0, 2.0) (3.0, -4.0) |
| (-2.0, 1.0) (-1.0, -3.0) (-3.0, 1.0) (0.0, 0.0) (2.0, -2.0) |
| . . . . . |
* *
This example shows the solution B <-- alpha(A-T)B, where A is a complex 5 by 5 upper triangular matrix that is not unit triangular, and B is a complex 5 by 1 rectangular matrix.
SIDE UPLO TRANSA DIAG M N ALPHA A LDA B LDB
| | | | | | | | | | |
CALL CTRSM( 'L' , 'U' , 'C' , 'N' , 5 , 1 , ALPHA , A , 6 , B , 6 )
ALPHA = (1.0, 0.0)
* *
| (-4.0, 1.0) (4.0, -3.0) (-1.0, 3.0) (0.0, 0.0) (-1.0, 0.0) |
| . (-2.0, 0.0) (-3.0, -1.0) (-2.0, -1.0) (4.0, 3.0) |
A = | . . (-5.0, 3.0) (-3.0, -3.0) (-5.0, -5.0) |
| . . . (4.0, -4.0) (2.0, 0.0) |
| . . . . (2.0, -1.0) |
| . . . . . |
* *
* *
| (-8.0, -19.0) |
| (8.0, 21.0) |
B = | (44.0, -8.0) |
| (13.0, -7.0) |
| (19.0, 2.0) |
| . |
* *
* *
| (3.0, 4.0) |
| (-4.0, 2.0) |
B = | (-5.0, 0.0) |
| (1.0, 3.0) |
| (3.0, 1.0) |
| . |
* *
These subroutines find the inverse of triangular matrix A:
Matrix A can be either upper or lower triangular, where:
| A | Subroutine |
| Short-precision real | STRI and STPI |
| Long-precision real | DTRI and DTPI |
| Fortran | CALL STRI | DTRI (uplo, diag, a, lda,
n)
CALL STPI | DTPI (uplo, diag, ap, n) |
| C and C++ | stri | dtri (uplo, diag, a, lda,
n);
stpi | dtpi (uplo, diag, ap, n); |
| PL/I | CALL STRI | DTRI (uplo, diag, a, lda,
n);
CALL STPI | DTPI (uplo, diag, ap, n); |
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
These subroutines find the inverse of triangular matrix A, where A is either upper or lower triangular:
where:
If n is 0, no computation is performed. See references [8] and [36].
Unable to allocate internal work area.
Matrix A is singular.
This example shows how the inverse of matrix A is computed, where A is a 5 by 5 upper triangular matrix that is not unit triangular and is stored in upper-triangular storage mode. Matrix A is:
* *
| 1.00 3.00 4.00 5.00 6.00 |
| 0.00 2.00 8.00 9.00 1.00 |
| 0.00 0.00 4.00 8.00 4.00 |
| 0.00 0.00 0.00 -2.00 6.00 |
| 0.00 0.00 0.00 0.00 -1.00 |
* *
and where the following inverse matrix is computed. Matrix A-1 is:
* *
| 1.00 -1.50 2.00 3.75 35.00 |
| 0.00 0.50 -1.00 -1.75 -14.00 |
| 0.00 0.00 0.25 1.00 7.00 |
| 0.00 0.00 0.00 -0.50 -3.00 |
| 0.00 0.00 0.00 0.00 -1.00 |
* *
UPLO DIAG A LDA N
| | | | |
CALL STRI( 'U' , 'N' , A , 5 , 5)
* *
| 1.00 3.00 4.00 5.00 6.00 |
| . 2.00 8.00 9.00 1.00 |
A = | . . 4.00 8.00 4.00 |
| . . . -2.00 6.00 |
| . . . . -1.00 |
* *
* *
| 1.00 -1.50 2.00 3.75 35.00 |
| . 0.50 -1.00 -1.75 -14.00 |
A = | . . 0.25 1.00 7.00 |
| . . . -0.50 -3.00 |
| . . . . -1.00 |
* *
This example shows how the inverse of matrix A is computed, where A is a 5 by 5 lower triangular matrix that is unit triangular and is stored in lower-triangular storage mode. Matrix A is:
* *
| 1.0 0.0 0.0 0.0 0.0 |
| 3.0 1.0 0.0 0.0 0.0 |
| 4.0 8.0 1.0 0.0 0.0 |
| 5.0 9.0 8.0 1.0 0.0 |
| 6.0 1.0 4.0 6.0 1.0 |
* *
and where the following inverse matrix is computed. Matrix A-1 is:
* *
| 1.0 0.0 0.0 0.0 0.0 |
| -3.0 1.0 0.0 0.0 0.0 |
| 20.0 -8.0 1.0 0.0 0.0 |
| -138.0 55.0 -8.0 1.0 0.0 |
| 745.0 -299.0 44.0 -6.0 1.0 |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO DIAG A LDA N
| | | | |
CALL STRI( 'L' , 'U' , A , 5 , 5)
* *
| . . . . . |
| 3.0 . . . . |
A = | 4.0 8.0 . . . |
| 5.0 9.0 8.0 . . |
| 6.0 1.0 4.0 6.0 . |
* *
* *
| . . . . . |
| -3.0 . . . . |
A = | 20.0 -8.0 . . . |
| -138.0 55.0 -8.0 . . |
| 745.0 -299.0 44.0 -6.0 . |
* *
This example shows how the inverse of matrix A is computed, where A is the same matrix shown in Example 1 and is stored in upper-triangular-packed storage mode. The inverse matrix computed here is the same as the inverse matrix shown in Example 1 and is stored in upper-triangular-packed storage mode.
UPLO DIAG AP N
| | | |
CALL STPI( 'U' , 'N' , AP , 5)
AP = (1.00, 3.00, 2.00, 4.00, 8.00, 4.00, 5.00, 9.00, 8.00,
-2.00, 6.00, 1.00, 4.00, 6.00, -1.00)
AP = (1.00, -1.50, 0.50, 2.00, -1.00, 0.25, 3.75, -1.75, 1.00,
-0.50, 35.00, -14.00, 7.00, -3.00, -1.00)
This example shows how the inverse of matrix A is computed, where A is the same matrix shown in Example 2 and is stored in lower-triangular-packed storage mode. The inverse matrix computed here is the same as the inverse matrix shown in Example 2 and is stored in lower-triangular-packed storage mode.
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO DIAG AP N
| | | |
CALL STPI( 'L' , 'U' , AP , 5)
AP = ( . , 3.0, 4.0, 5.0, 6.0, . , 8.0, 9.0, 1.0, . , 8.0, 4.0,
. , 6.0, . )
AP = ( . , -3.0, 20.0, -138.0, 745.0, . , -8.0, 55.0, -299.0,
. , -8.0, 44.0, . , -6.0, . )
This section contains the banded linear algebraic equation subroutine descriptions.
These subroutines factor general band matrix A, stored in
general-band storage mode, using Gaussian elimination. To solve the system of
equations with one or more right-hand sides, follow the call to these
subroutines with one or more calls to SGBS or DGBS, respectively.
| A | Subroutine |
| Short-precision real | SGBF |
| Long-precision real | DGBF |
| Note: | The output from these factorization subroutines should be used only as input to the solve subroutines SGBS and DGBS, respectively. |
| Fortran | CALL SGBF | DGBF (agb, lda, n, ml, mu, ipvt) |
| C and C++ | sgbf | dgbf (agb, lda, n, ml, mu, ipvt); |
| PL/I | CALL SGBF | DGBF (agb, lda, n, ml, mu, ipvt); |
The general band matrix A, stored in general-band storage mode, is factored using Gaussian elimination with partial pivoting to compute the LU factorization of A, where:
The transformed matrix A contains U in packed format, along with the multipliers necessary to construct, with the help of ipvt, a matrix L, such that A = LU. This factorization can then be used by SGBS or DGBS, respectively, to solve the system of equations. See reference [38].
Unable to allocate internal work area.
Matrix A is singular.
This example shows a factorization of a general band matrix A of order 9, with a lower band width of 2 and an upper band width of 3. On input matrix A is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 |
| 4.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 0.0 5.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 |
| 0.0 0.0 6.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 0.0 0.0 0.0 7.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 8.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 9.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 10.0 11.0 12.0 |
* *
Matrix A is stored in general-band storage mode in the two-dimensional array AGB of size LDA by N, where LDA = 2ml+mu+16 = 23. The array AGB is declared as AGB(1:23,1:9).
| Note: | Matrix A is the same matrix used in the examples in subroutines SGEF and DGEF (see "Example 1") and SGEFCD and DGEFCD (see "Example"). |
AGB LDA N ML MU IPVT )
| | | | | |
CALL SGBF( AGB , 23 , 9 , 2 , 3 , IPVT )
* *
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
| 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 12.0000 |
| 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 11.0000 0.0000 |
| 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
AGB = | 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
* *
* *
| 0.0000 0.0000 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 |
| 0.0000 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 12.0000 |
| 0.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 11.0000 0.3111 |
| 0.2500 0.2000 0.1600 0.1400 0.1250 0.1100 0.1000 5.5380 -325.00 |
| 0.0000 0.1500 0.0000 0.0714 0.0000 -0.0556 -0.0306 0.9385 0.0000 |
| 0.2500 0.1500 0.1000 0.0714 -0.0714 -0.0694 -0.0194 0.0000 0.0000 |
| 0.2500 0.0000 0.1000 0.0000 0.0536 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
AGB = | 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
| 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 |
* *
IPVT = (2, -65534, -131070, -196606, -262142, -327678, -327678,
-327680, -327680)
These subroutines solve the system Ax = b for
x, where A is a general band matrix, and x
and b are vectors. They use the results of the factorization of
matrix A, produced by a preceding call to SGBF or DGBF,
respectively.
| A, b, x | Subroutine |
| Short-precision real | SGBS |
| Long-precision real | DGBS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGBF and DGBF, respectively. |
| Fortran | CALL SGBS | DGBS (agb, lda, n, ml, mu, ipvt, bx) |
| C and C++ | sgbs | dgbs (agb, lda, n, ml, mu, ipvt, bx); |
| PL/I | CALL SGBS | DGBS (agb, lda, n, ml, mu, ipvt, bx); |
Specified as: a one-dimensional array of (at least) length n, containing fullword integers.
The real system Ax = b is solved for x, where A is a real general band matrix, stored in general-band storage mode, and x and b are vectors. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SGBF or DGBF, respectively. The transformed matrix A, used by this computation, consists of the upper triangular matrix U and the multipliers necessary to construct L using ipvt, as defined in "Function". See reference [38].
| Note: | If the factorization performed by SGBF or DGBF failed due to a singular matrix argument, the results returned by this subroutine are unpredictable, and there may be a divide-by-zero program exception message. |
This example shows how to solve the system Ax = b, where general band matrix A is the same matrix factored in "Example" for SGBF and DGBF. The input for AGB and IPVT in this example is the same as the output for that example.
AGB LDA N ML MU IPVT BX
| | | | | | |
CALL SGBS( AGB , 23 , 9 , 2 , 3 , IPVT , BX )
IPVT = (2, -65534, -131070, -196606, -262142, -327678, -327678,
-327680, -327680)
BX = (4.0000, 5.0000, 9.0000, 10.0000, 11.0000, 12.0000,
12.0000, 12.0000, 33.0000)
AGB =(same as output AGB in
"Example")
BX = (1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
0.9999, 1.0001)
These subroutines factor positive definite symmetric band matrix A, stored in lower-band-packed storage mode, using:
To solve the system of equations with one or more right-hand sides, follow
the call to these subroutines with one or more calls to SPBS, DPBS, SPBCHS, or
DPBCHS, respectively.
| A | Subroutine |
| Short-precision real | SPBF and SPBCHF |
| Long-precision real | DPBF and DPBCHF |
Notes:
| Fortran | CALL SPBF | DPBF | SPBCHF | DPBCHF (apb, lda, n, m) |
| C and C++ | spbf | dpbf | spbchf | dpbchf (apb, lda, n, m); |
| PL/I | CALL SPBF | DPBF | SPBCHF | DPBCHF (apb, lda, n, m); |
The positive definite symmetric band matrix A, stored in lower-band-packed storage mode, is factored using Gaussian elimination in SPBF and DPBF and Cholesky factorization in SPBCHF and DPBCHF. The transformed matrix A contains the results of the factorization in packed format. This factorization can then be used by SPBS, DPBS, SPBCHS, and DPBCHS, respectively, to solve the system of equations.
For performance reasons, divides are done in a way that reduces the effective exponent range for which DPBF works properly, when processing narrow band widths; therefore, you may want to scale your problem.
Unable to allocate internal work area.
This example shows a factorization of a real positive definite symmetric band matrix A of order 9, using Gaussian elimination, where on input, matrix A is:
* *
| 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 2.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 3.0 2.0 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 2.0 3.0 2.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 2.0 3.0 2.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 2.0 3.0 2.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 3.0 2.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 3.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 3.0 |
* *
and on output, matrix A is:
* *
| 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 1.0 1.0 1.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 |
* *
where array location APB(2,9) is set to 0.0.
APB LDA N M
| | | |
CALL SPBF( APB , 3 , 9 , 2 )
* *
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
APB = | 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 . |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . . |
* *
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
APB = | 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . . |
* *
This example shows a Cholesky factorization of the same matrix used in Example 1.
APB LDA N M
| | | |
CALL SPBCHF( APB , 3 , 9 , 2 )
APB =(same as input APB in Example 1)
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
APB = | 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 . . |
* *
These subroutines solve the system Ax = b for x, where A is a positive definite symmetric band matrix, and x and b are vectors. They use the results of the factorization of matrix A, produced by a preceding call to SPBF, DPBF, SPBCHF, and DPBCHF, respectively, where:
| A, b, x | Subroutine |
| Short-precision real | SPBS and SPBCHS |
| Long-precision real | DPBS and DPBCHS |
Notes:
| Fortran | CALL SPBS | DPBS | SPBCHS | DPBCHS (apb, lda, n, m, bx) |
| C and C++ | spbs | dpbs | spbchs | dpbchs (apb, lda, n, m, bx); |
| PL/I | CALL SPBS | DPBS | SPBCHS | DPBCHS (apb, lda, n, m, bx); |
The system Ax = b is solved for x, where A is a positive definite symmetric band matrix, stored in lower-band-packed storage mode, and x and b are vectors. These subroutines use the results of the factorization of matrix A, produced by a preceding call to SPBF, DPBF, SPBCHF, or DPBCHF, respectively.
None
| Note: | If the factorization subroutine resulted in a nonpositive definite matrix, error 2104 for SPBF and DPBF or error 2115 for SPBCHF and DPBCHF, results of these subroutines may be unpredictable. |
This example shows how to solve the system Ax = b, where matrix A is the same matrix factored in the "Example 1" for SPBF and DPBF, using Gaussian elimination.
APB LDA N M BX
| | | | |
CALL SPBS( APB , 3 , 9 , 2 , BX )
APB =(same as output APB in "Example 1") BX = (3.0, 6.0, 9.0, 9.0, 9.0, 9.0, 9.0, 8.0, 6.0)
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
This example shows how to solve the system Ax = b, where matrix A is the same matrix factored in the "Example 2" for SPBCHF and DPBCHF, using Cholesky factorization.
APB LDA N M BX
| | | | |
CALL SPBCHS( APB , 3 , 9 , 2 , BX )
APB =(same as output APB in "Example 2") BX = (3.0, 6.0, 9.0, 9.0, 9.0, 9.0, 9.0, 8.0, 6.0)
BX = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
These subroutines compute the standard Gaussian factorization with partial
pivoting for tridiagonal matrix A, stored in tridiagonal storage
mode. To solve a tridiagonal system with one or more right-hand sides, follow
the call to these subroutines with one or more calls to SGTS or DGTS,
respectively.
| c, d, e, f | Subroutine |
| Short-precision real | SGTF |
| Long-precision real | DGTF |
| Note: | The output from these factorization subroutines should be used only as input to the solve subroutines SGTS and DGTS, respectively. |
| Fortran | CALL SGTF | DGTF (n, c, d, e, f, ipvt) |
| C and C++ | sgtf | dgtf (n, c, d, e, f, ipvt); |
| PL/I | CALL SGTF | DGTF (n, c, d, e, f, ipvt); |
The standard Gaussian elimination with partial pivoting of tridiagonal matrix A is computed. The factorization is returned by overwriting input arrays C, D, and E, and by writing into output array F, along with pivot information in vector ipvt. This factorization can then be used by SGTS or DGTS, respectively, to solve tridiagonal systems of linear equations. See references [43], [51], [52], and [84]. If n is 0, no computation is performed.
Matrix A is singular or nearly singular.
n < 0
This example shows how to factor the following tridiagonal matrix A of order 4:
* *
| 2.0 2.0 0.0 0.0 |
| 1.0 3.0 2.0 0.0 |
| 0.0 1.0 3.0 2.0 |
| 0.0 0.0 1.0 3.0 |
* *
N C D E F IPVT
| | | | | |
CALL DGTF( 4 , C , D , E , F , IPVT )
C = ( . , 1.0, 1.0, 1.0)
D = (2.0, 3.0, 3.0, 3.0)
E = (2.0, 2.0, 2.0, . )
C = ( . , -0.5, -0.5, -0.5) D = (-0.5, -0.5, -0.5, -0.5) E = (2.0, 2.0, 2.0, . ) IPVT = (X'00', X'00', X'00', X'00')
These subroutines solve a tridiagonal system of linear equations using the
factorization of tridiagonal matrix A, stored in tridiagonal storage
mode, produced by SGTF or DGTF, respectively.
| c, d, e, f, b, x | Subroutine |
| Short-precision real | SGTS |
| Long-precision real | DGTS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGTF and DGTF, respectively. |
| Fortran | CALL SGTS | DGTS (n, c, d, e, f, ipvt, bx) |
| C and C++ | sgts | dgts (n, c, d, e, f, ipvt, bx); |
| PL/I | CALL SGTS | DGTS (n, c, d, e, f, ipvt, bx); |
Given the factorization produced by SGTF or DGTF, respectively, these subroutines use the standard forward elimination and back substitution to solve the tridiagonal system Ax = b, where A is a general tridiagonal matrix. See references [43], [51], [52], and [84].
None
n < 0
This example solves the tridiagonal system Ax = b, where matrix A is the same matrix factored in "Example" for SGTF and DGTF, and where:
b = (4.0, 6.0, 6.0, 4.0)
x = (1.0, 1.0, 1.0, 1.0)
N C D E F IPVT BX
| | | | | | |
CALL DGTS( 4 , C , D , E , F , IPVT , BX )
C =(same as output C in "Example") D =(same as output D in "Example") E =(same as output E in "Example") F =(same as output F in "Example") IPVT =(same as output IPVT in "Example") BX =(4.0, 6.0, 6.0, 4.0, . )
BX = (1.0, 1.0, 1.0, 1.0, . )
These subroutines solve the tridiagonal system
Ax = b using Gaussian elimination, where
tridiagonal matrix A is stored in tridiagonal storage mode.
| c, d, e, b, x | Subroutine |
| Short-precision real | SGTNP |
| Long-precision real | DGTNP |
| Short-precision complex | CGTNP |
| Long-precision complex | ZGTNP |
| Note: |
In general, these subroutines provide better performance than the _GTNPF and
_GTNPS subroutines; however, in the following instances, you get better
performance by using _GTNPF and _GTNPS:
|
| Fortran | CALL SGTNP | DGTNP | CGTNP | ZGTNP (n, c, d, e, bx) |
| C and C++ | sgtnp | dgtnp | cgtnp | zgtnp (n, c, d, e, bx); |
| PL/I | CALL SGTNP | DGTNP | CGTNP | ZGTNP (n, c, d, e, bx); |
For a description of how tridiagonal matrices are stored, see "General Tridiagonal Matrix".
The solution of the tridiagonal system Ax = b is computed by Gaussian elimination.
No pivoting is done. Therefore, these subroutines should not be used when pivoting is necessary to maintain the numerical accuracy of the solution. Overflow may occur if small main diagonal elements are generated. Underflow or accuracy loss may occur if large main diagonal elements are generated.
For performance reasons, complex divides are done without scaling. Computing the inverse in this way restricts the range of numbers for which the ZGTNP subroutine works properly.
For performance reasons, divides are done in a way that reduces the effective exponent range for which DGTNP and ZGTNP work properly; therefore, you may want to scale your problem, such that the diagonal elements are close to 1.0 for DGTNP and (1.0, 0.0) for ZGTNP.
None
n < 0
This example shows a factorization of the real tridiagonal matrix A, of order 4:
* *
| 7.0 4.0 0.0 0.0 |
| 1.0 8.0 5.0 0.0 |
| 0.0 2.0 9.0 6.0 |
| 0.0 0.0 3.0 10.0 |
* *
It then finds the solution of the tridiagonal system Ax = b, where b is:
(11.0, 14.0, 17.0, 13.0)
and x is:
(1.0, 1.0, 1.0, 1.0)
On output, arrays C, D, and E are overwritten.
N C D E BX
| | | | |
CALL DGTNP( 4 , C , D , E , BX )
C = ( . , 1.0, 2.0, 3.0)
D = (7.0, 8.0, 9.0, 10.0)
E = (4.0, 5.0, 6.0, . )
BX = (11.0, 14.0, 17.0, 13.0)
BX = (1.0, 1.0, 1.0, 1.0)
This example shows a factorization of the complex tridiagonal matrix A, of order 4:
* *
| (7.0, 7.0) (4.0, 4.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, 1.0) (8.0, 8.0) (5.0, 5.0) (0.0, 0.0) |
| (0.0, 0.0) (2.0, 2.0) (9.0, 9.0) (6.0, 6.0) |
| (0.0, 0.0) (0.0, 0.0) (3.0, 3.0) (10.0, 10.0) |
* *
It then finds the solution of the tridiagonal system Ax = b, where b is:
((-11.0,19.0), (-14.0,50.0), (-17.0,93.0), (-13.0,85.0))
and x is:
((1.0,-1.0), (2.0,-2.0), (3.0,-3.0), (4.0,-4.0))
On output, arrays C, D, and E are overwritten.
N C D E BX
| | | | |
CALL ZGTNP( 4 , C , D , E , BX )
C = ( . , (1.0, 1.0), (2.0, 2.0), (3.0, 3.0))
D = ((7.0, 7.0), (8.0, 8.0), (9.0, 9.0), (10.0, 10.0))
E = ((4.0, 4.0), (5.0, 5.0), (6.0, 6.0), . )
BX = ((-11.0, 19.0), (-14.0, 50.0), (-17.0, 93.0), (-13.0, 85.0))
BX = ((0.0, 1.0), (1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
These subroutines factor tridiagonal matrix A, stored in
tridiagonal storage mode, using Gaussian elimination. To solve a tridiagonal
system of linear equations with one or more right-hand sides, follow the call
to these subroutines with one or more calls to SGTNPS, DGTNPS, CGTNPS, or
ZGTNPS, respectively.
| c, d, e | Subroutine |
| Short-precision real | SGTNPF |
| Long-precision real | DGTNPF |
| Short-precision complex | CGTNPF |
| Long-precision complex | ZGTNPF |
Notes:
| Fortran | CALL SGTNPF | DGTNPF | CGTNPF | ZGTNPF (n, c, d, e, iopt) |
| C and C++ | sgtnpf | dgtnpf | cgtnpf | zgtnpf (n, c, d, e, iopt); |
| PL/I | CALL SGTNPF | DGTNPF | CGTNPF | ZGTNPF (n, c, d, e, iopt); |
Specified as: a fullword integer; iopt = 0 or 1.
For a description of how tridiagonal matrices are stored, see "General Tridiagonal Matrix".
The factorization of a diagonally-dominant tridiagonal matrix A is computed using Gaussian elimination, This factorization can then be used by SGTNPS, DGTNPS, CGTNPS, or ZGTNPS respectively, to solve the tridiagonal systems of linear equations. See reference [71].
No pivoting is done by these subroutines. Therefore, these subroutines should not be used when pivoting is necessary to maintain the numerical accuracy of the solution. Overflow may occur if small main diagonal elements are generated. Underflow or accuracy loss may occur if large main diagonal elements are generated.
For performance reasons, complex divides are done without scaling. Computing the inverse in this way restricts the range of numbers for which ZGTNPF works properly.
For performance reasons, divides are done in a way that reduces the effective exponent range for which DGTNPF and ZGTNPF work properly; therefore, you may want to scale your problem, such that the diagonal elements are close to 1.0 for DGTNPF and (1.0, 0.0) for ZGTNPF.
None
This example shows a factorization of the tridiagonal matrix A, of order 4:
* *
| 1.0 1.0 0.0 0.0 |
| 1.0 2.0 1.0 0.0 |
| 0.0 1.0 3.0 1.0 |
| 0.0 0.0 1.0 1.0 |
* *
N C D E IOPT
| | | | |
CALL DGTNPF( 4 , C , D , E , 0 )
C = ( . , 1.0, 1.0, 1.0)
D = (1.0, 2.0, 3.0, 1.0)
E = (1.0, 1.0, 1.0, . )
C = ( . , -1.0, -1.0, 1.0) D = (-1.0, -1.0, -1.0, -1.0) E = (1.0, 1.0, -1.0, . )
This example shows a factorization of the tridiagonal matrix A, of order 4:
* *
| (7.0, 7.0) (4.0, 4.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, 1.0) (8.0, 8.0) (5.0, 5.0) (0.0, 0.0) |
| (0.0, 0.0) (2.0, 2.0) (9.0, 9.0) (6.0, 6.0) |
| (0.0, 0.0) (0.0, 0.0) (3.0, 3.0) (10.0, 10.0) |
* *
N C D E IOPT
| | | | |
CALL ZGTNPF( 4 , C , D , E , 0 )
C = ( . , (1.0, 1.0), (2.0, 2.0), (3.0, 3.0))
D = ((7.0, 7.0), (8.0, 8.0), (9.0, 9.0), (10.0, 10.0))
E = ((4.0, 4.0), (5.0, 5.0), (6.0, 6.0), . )
C = ( . , (-0.142, 0.0), (-0.269, 0.0), (3.0, 3.0))
D = ((-0.0714, 0.0714), (-0.0673, 0.0673), (-0.0854, 0.0854),
(-0.05, 0.05))
E = ((4.0, 4.0), (5.0, 5.0), (-0.6, 0.0), . )
These subroutines solve a tridiagonal system of equations using the
factorization of matrix A, stored in tridiagonal storage mode,
produced by SGTNPF, DGTNPF, CGTNPF, or ZGTNPF, respectively.
| c, d, e, b, x | Subroutine |
| Short-precision real | SGTNPS |
| Long-precision real | DGTNPS |
| Short-precision complex | CGTNPS |
| Long-precision complex | ZGTNPS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SGTNPF, DGTNPF, CGTNPF, and ZGTNPF, respectively. |
| Fortran | CALL SGTNPS | DGTNPS | CGTNPS | ZGTNPS (n, c, d, e, bx) |
| C and C++ | sgtnps | dgtnps | cgtnps | zgtnps (n, c, d, e, bx); |
| PL/I | CALL SGTNPS | DGTNPS | CGTNPS | ZGTNPS (n, c, d, e, bx); |
For a description of how tridiagonal matrices are stored, see "General Tridiagonal Matrix".
The solution of tridiagonal system Ax = b is computed using the factorization produced by SGTNPF, DGTNPF, CGTNPF, or ZGTNPF, respectively. The factorization is based on Gaussian elimination. See reference [71].
None
n < 0
This example finds the solution of tridiagonal system Ax = b, where matrix A is the same matrix factored in "Example 1" for SGTNPF and DGTNPF. b is:
(2.0, 4.0, 5.0, 2.0)
and x is:
(1.0, 1.0, 1.0, 1.0)
N C D E BX
| | | | |
CALL DGTNPS( 4 , C , D , E , BX )
C =(same as output C in "Example 1") D =(same as output D in "Example 1") E =(same as output E in "Example 1") BX =(2.0, 4.0, 5.0, 2.0)
BX = (1.0, 1.0, 1.0, 1.0)
This example finds the solution of tridiagonal system Ax = b, where matrix A is the same matrix factored in "Example 2" for CGTNPF and ZGTNPF. b is:
((-11.0,19.0), (-14.0,50.0), (-17.0,93.0), (-13.0,85.0))
and x is:
((0.0,1.0), (1.0,2.0), (2.0,3.0), (3.0,4.0))
N C D E BX
| | | | |
CALL ZGTNPS( 4 , C , D , E , BX )
C =(same as output C in "Example 2") D =(same as output D in "Example 2") E =(same as output E in "Example 2") BX =((-11.0, 19.0), (-14.0, 50.0), (-17.0, 93.0), (-13.0, 85.))
BX = ((0.0, 1.0), (1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
These subroutines factor symmetric tridiagonal matrix A, stored in
symmetric-tridiagonal storage mode, using Gaussian elimination. To solve a
tridiagonal system of linear equations with one or more right-hand sides,
follow the call to these subroutines with one or more calls to SPTS or DPTS,
respectively.
| c, d | Subroutine |
| Short-precision real | SPTF |
| Long-precision real | DPTF |
| Note: | The output from these factorization subroutines should be used only as input to the solve subroutines SPTS and DPTS, respectively. |
| Fortran | CALL SPTF | DPTF (n, c, d, iopt) |
| C and C++ | sptf | dptf (n, c, d, iopt); |
| PL/I | CALL SPTF | DPTF (n, c, d, iopt); |
Specified as: a fullword integer; iopt = 0 or 1.
For a description of how positive definite symmetric tridiagonal matrices are stored, see "Positive Definite Symmetric Tridiagonal Matrix".
The factorization of positive definite symmetric tridiagonal matrix A is computed using Gaussian elimination. This factorization can then be used by SPTS or DPTS, respectively, to solve the tridiagonal systems of linear equations. See reference [71].
No pivoting is done. Therefore, these subroutines should not be used when pivoting is necessary to maintain the numerical accuracy of the solution. Overflow may occur if small pivots are generated.
For performance reasons, divides are done in a way that reduces the effective exponent range for which DPTF works properly; therefore, you may want to scale your problem, such that the diagonal elements are close to 1.0 for DPTF.
None
| Note: | There is no test for positive definiteness in these subroutines. |
This example shows a factorization of the tridiagonal matrix A, of order 4:
* *
| 1.0 1.0 0.0 0.0 |
| 1.0 2.0 1.0 0.0 |
| 0.0 1.0 3.0 1.0 |
| 0.0 0.0 1.0 1.0 |
* *
N C D IOPT
| | | |
CALL DPTF( 4 , C , D , 0 )
C = ( . , 1.0, 1.0, 1.0)
D = (1.0, 2.0, 3.0, 1.0)
C = ( . , -1.0, -1.0, -1.0) D = (-1.0, -1.0, -1.0, -1.0)
These subroutines solve a positive definite symmetric tridiagonal system of
equations using the factorization of matrix A, stored in
symmetric-tridiagonal storage mode, produced by SPTF and DPTF, respectively.
| c, d, b, x | Subroutine |
| Short-precision real | SPTS |
| Long-precision real | DPTS |
| Note: | The input to these solve subroutines must be the output from the factorization subroutines SPTF and DPTF, respectively. |
| Fortran | CALL SPTS | DPTS (n, c, d, bx) |
| C and C++ | spts | dpts (n, c, d, bx); |
| PL/I | CALL SPTS | DPTS (n, c, d, bx); |
For a description of how tridiagonal matrices are stored, see "Positive Definite or Negative Definite Symmetric Matrix".
The solution of positive definite symmetric tridiagonal system Ax = b is computed using the factorization produced by SPTF or DPTF, respectively. The factorization is based on Gaussian elimination. See reference [71].
None
n < 0
This example finds the solution of tridiagonal system Ax = b, where matrix A is the same matrix factored in "Example" for SPTF and DPTF. b is:
(2.0, 4.0, 5.0, 2.0)
and x is:
(1.0, 1.0, 1.0, 1.0)
N C D BX
| | | |
CALL DPTS( 4 , C , D , BX )
C = ( . , -1.0, -1.0, -1.0)
D = (-1.0, -1.0, -1.0, -1.0)
BX = (2.0, 4.0, 5.0, 2.0)
BX = (1.0, 1.0, 1.0, 1.0)
STBSV and DTBSV solve one of the following triangular banded systems of
equations with a single right-hand side, using the vector x and
triangular band matrix A or its transpose:
| Solution | Equation |
|---|---|
| 1. x <-- A-1x | Ax = b |
| 2. x <-- A-Tx | ATx = b |
CTBSV and ZTBSV solve one of the following triangular banded systems of
equations with a single right-hand side, using the vector x and
triangular band matrix A, its transpose, or its conjugate
transpose:
| Solution | Equation |
|---|---|
| 1. x <-- A-1x | Ax = b |
| 2. x <-- A-Tx | ATx = b |
| 3. x <-- A-Hx | AHx = b |
Matrix A can be either upper or lower triangular and is stored
in upper- or lower-triangular-band-packed storage mode, respectively.
| A, x | Subprogram |
| Short-precision real | STBSV |
| Long-precision real | DTBSV |
| Short-precision complex | CTBSV |
| Long-precision complex | ZTBSV |
| Fortran | CALL STBSV | DTBSV | CTBSV | ZTBSV (uplo, trans, diag, n, k, a, lda, x, incx) |
| C and C++ | stbsv | dtbsv | ctbsv | ztbsv (uplo, trans, diag, n, k, a, lda, x, incx); |
| PL/I | CALL STBSV | DTBSV | CTBSV | ZTBSV (uplo, trans, diag, n, k, a, lda, x, incx); |
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If trans = 'N', A is used, resulting in solution 1.
If trans = 'T', AT is used, resulting in solution 2.
If trans = 'C', AH is used, resulting in solution 3.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
These subroutines solve a triangular banded system of equations with a single right-hand side. The solution, x, may be any of the following, where triangular band matrix A, its transpose, or its conjugate transpose is used, and where A can be either upper- or lower-triangular:
where:
See references [34], [46], and [38]. If n is 0, no computation is performed.
None
This example shows the solution x <-- A-1x. Matrix A is a real 9 by 9 upper triangular band matrix with an upper band width of 2 that is not unit triangular, stored in upper-triangular-band-packed storage mode. Vector x is a vector of length 9, where matrix A is:
* *
| 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 4.0 2.0 3.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 4.0 1.0 1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 4.0 2.0 2.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 3.0 1.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 3.0 2.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 3.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 2.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
* *
UPLO TRANS DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBSV( 'U' , 'N' , 'N' , 9 , 2 , A , 3 , X , 1 )
* *
| . . 1.0 3.0 1.0 2.0 1.0 2.0 0.0 |
A = | . 1.0 2.0 1.0 2.0 1.0 2.0 1.0 2.0 |
| 1.0 4.0 4.0 4.0 3.0 3.0 3.0 2.0 1.0 |
* *
X = (2.0, 7.0, 1.0, 8.0, 2.0, 8.0, 1.0, 8.0, 3.0)
X = (1.0, 1.0, 0.0, 1.0, 0.0, 2.0, 0.0, 1.0, 3.0)
This example shows the solution x <-- A-Tx, solving the same system as in Example 1. Matrix A is a real 9 by 9 lower triangular band matrix with a lower band width of 2 that is not unit triangular, stored in lower-triangular-band-packed storage mode. Vector x is a vector of length 9 where matrix A is:
* *
| 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 4.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 4.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 3.0 1.0 4.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 2.0 3.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 2.0 1.0 3.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 3.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 2.0 1.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.0 1.0 |
* *
UPLO TRANS DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBSV( 'L' , 'T' , 'N' , 9 , 2 , A , 3 , X , 1 )
* *
| 1.0 4.0 4.0 4.0 3.0 3.0 3.0 2.0 1.0 |
A = | 1.0 2.0 1.0 2.0 1.0 2.0 1.0 2.0 . |
| 1.0 3.0 1.0 2.0 1.0 2.0 0.0 . . |
* *
X =(same as input X in Example 1)
X =(same as output X in Example 1)
This example shows the solution x <-- A-Tx, where k > n. Matrix A is a real 4 by 4 upper triangular band matrix with an upper band width of 3, even though k is specified as 5. It is not unit triangular and is stored in upper-triangular-band-packed storage mode. Vector x is a vector of length 4 where matrix A is:
* *
| 1.0 2.0 3.0 2.0 |
| 0.0 2.0 2.0 5.0 |
| 0.0 0.0 3.0 3.0 |
| 0.0 0.0 0.0 1.0 |
* *
UPLO TRANS DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBSV( 'U' , 'T' , 'N' , 4 , 5 , A , 6 , X , 1 )
* *
| . . . . |
| . . . . |
A = | . . . 2.0 |
| . . 3.0 5.0 |
| . 2.0 2.0 3.0 |
| 1.0 2.0 3.0 1.0 |
* *
X = (5.0, 18.0, 32.0, 41.0)
X = (5.0, 4.0, 3.0, 2.0)
This example shows the solution x <-- A-Tx. Matrix A is a complex 7 by 7 lower triangular band matrix with a lower band width of 3 that is not unit triangular, stored in lower-triangular-band-packed storage mode. Vector x is a vector of length 7. Matrix A is:
* *
| (1.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, 2.0) (2.0, 1.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, 3.0) (2.0, 2.0) (3.0, 1.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, 4.0) (2.0, 3.0) (3.0, 3.0) (4.0, 1.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (0.0, 0.0) (2.0, 4.0) (3.0, 3.0) (4.0, 2.0) (2.0, 1.0) (0.0, 0.0) (0.0, 0.0) |
| (0.0, 0.0) (0.0, 0.0) (3.0, 3.0) (4.0, 3.0) (5.0, 1.0) (3.0, 1.0) (0.0, 0.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (4.0, 4.0) (5.0, 2.0) (6.0, 1.0) (2.0, 1.0) |
* *
UPLO TRANS DIAG N K A LDA X INCX
| | | | | | | | |
CALL CTBSV( 'L' , 'T' , 'N' , 7 , 3 , A , 4 , X , 1 )
* *
| (1.0, 0.0) (2.0, 1.0) (3.0, 1.0) (4.0, 1.0) (2.0, 1.0) (3.0, 1.0) (2.0, 1.0) |
A = | (1.0, 2.0) (2.0, 2.0) (3.0, 3.0) (4.0, 2.0) (5.0, 1.0) (6.0, 1.0) . |
| (1.0, 3.0) (2.0, 3.0) (3.0, 3.0) (4.0, 3.0) (5.0, 2.0) . . |
| (1.0, 4.0) (2.0, 4.0) (3.0, 3.0) (4.0, 4.0) . . . |
* *
X = ((2.0, 2.0), (7.0, 1.0), (1.0, 1.0), (8.0, 1.0),
(2.0, 0.0), (8.0, 1.0), (1.0, 2.0))
X = ((-12.048, -13.136), (6.304, -1.472), (-1.880, 1.040),
(2.600, -1.800), (-2.160, 1.880), (0.800, -1.400),
(0.800, 0.600))
This section contains the sparse linear algebraic equation subroutine descriptions.
This subroutine factors sparse matrix A by Gaussian elimination, using a modified Markowitz count with threshold pivoting. The sparse matrix can be stored by indices, rows, or columns. To solve the system of equations, follow the call to this subroutine with a call to DGSS.
| Fortran | CALL DGSF (iopt, n, nz, a, ia, ja, lna, iparm, rparm, oparm, aux, naux) |
| C and C++ | dgsf (iopt, n, nz, a, ia, ja, lna, iparm, rparm, oparm, aux, naux); |
| PL/I | CALL DGSF (iopt, n, nz, a, ia, ja, lna, iparm, rparm, oparm, aux, naux); |
If iopt = 0, it is stored by indices.
If iopt = 1, it is stored by rows.
If iopt = 2, it is stored by columns.
Specified as: a fullword integer; iopt = 0, 1, or 2.
If iopt = 0, it contains the row numbers that correspond to the elements in array A.
If iopt = 1, it contains the row pointers.
If iopt = 2, it contains the row numbers that correspond to the elements in array A.
Specified as: an array of length lna, containing fullword integers; IA(i) >= 1. See "Sparse Matrix" for more information on storage techniques.
If iopt = 0, it contains the column numbers that correspond to the elements in array A.
If iopt = 1, it contains the column numbers that correspond to the elements in array A.
If iopt = 2, it contains the column pointers.
Specified as: an array of length lna, containing fullword integers; JA(i) >= 1. See "Sparse Matrix" for more information on storage techniques.
The size of lna depends on the structure of the input matrix. The requirement that lna > 2nz does not guarantee a successful run of the program. If the input matrix is expected to have many fill-ins, lna should be set larger. Larger lna may result in a performance improvement.
For details on how lna relates to storage compressions, see "Performance and Accuracy Considerations".
If IPARM(1) = 0, the following default values are used:
If IPARM(1) = 1, the default values are not used.
If IPARM(3) = 0, this subroutine checks the values in arrays IA and JA.
If IPARM(3) = 1, this subroutine assumes that the input values are correct in arrays IA and JA.
If IPARM(4) = 0, this computation is not performed.
If IPARM(4) = 1, this subroutine computes:
These values are stored in OPARM(2) and OPARM(3), respectively.
Specified as: a one-dimensional array of (at least) length 5, containing long-precision real numbers, where the rparm values must be:
For additional information about rparm, see "Performance and Accuracy Considerations".
Returned as: a one-dimensional array of length 5, containing long-precision real numbers.
The matrix A is factored by Gaussian elimination, using a modified Markowitz count with threshold pivoting to compute the sparse LU factorization of A:
where:
To solve the system of equations, follow the call to this subroutine with a call to DGSS. If n is 0, no computation is performed. See references [10], [47], and [87].
This example factors 5 by 5 sparse matrix A, which is stored by indices in arrays A, IA, and JA. The three storage techniques are shown in this example, and the output is the same regardless of the storage technique used. The matrix is factored using Gaussian elimination with threshold pivoting. Matrix A is:
* *
| 2.0 0.0 4.0 0.0 0.0 |
| 1.0 1.0 0.0 0.0 3.0 |
| 0.0 0.0 3.0 4.0 0.0 |
| 2.0 2.0 0.0 1.0 5.0 |
| 0.0 0.0 1.0 1.0 0.0 |
* *
| Note: | In this example, only nonzero elements are used as input to the matrix. |
IOPT N NZ A IA JA LNA IPARM RPARM OPARM AUX NAUX
| | | | | | | | | | | |
CALL DGSF( 0 , 5, 13, A, IA, JA, 27 , IPARM, RPARM, OPARM, AUX, 150 )
A = (2.0, 1.0, 1.0, 3.0, 4.0, 1.0, 5.0, 2.0, 2.0, 1.0, 1.0,
4.0, 3.0, . , . , . , . , . , . , . , . , . , . , . , . ,
. , . )
IA = (1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 1, 2, . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
JA = (1, 1, 2, 3, 4, 4, 5, 1, 2, 3, 4, 3, 5, . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
IPARM = (1, 3, 1, 1)
RPARM = (1.D-12, 0.1D0)
IOPT N NZ A IA JA LNA IPARM RPARM OPARM AUX NAUX
| | | | | | | | | | | |
CALL DGSF( 1 , 5, 13, A, IA, JA, 27 , IPARM, RPARM, OPARM, AUX, 150 )
A = (2.0, 4.0, 1.0, 1.0, 3.0, 3.0, 4.0, 2.0, 2.0, 1.0, 5.0,
1.0, 1.0, . , . , . , . , . , . , . , . , . , . , . , . ,
. , . )
IA = (1, 3, 6, 8, 12, 14, . , . , . , . , . , . , . , . , . ,
. , . , . , . , . )
JA = (1, 3, 1, 2, 5, 3, 4, 1, 2, 4, 5, 3, 4, . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
IPARM = (1, 3, 1, 1)
RPARM = (1.D-12, 0.1D0)
IOPT N NZ A IA JA LNA IPARM RPARM OPARM AUX NAUX
| | | | | | | | | | | |
CALL DGSF( 2 , 5, 13, A, IA, JA, 27 , IPARM, RPARM, OPARM, AUX, 150 )
A = (2.0, 1.0, 2.0, 1.0, 2.0, 4.0, 3.0, 1.0, 4.0, 1.0, 1.0,
3.0, 5.0, . , . , . , . , . , . , . , . , . , . , . , . ,
. , . )
IA = (1, 2, 4, 2, 4, 1, 3, 5, 3, 4, 5, 2, 4, . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
JA = (1, 4, 6, 9, 12, 14, . , . , . , . , . , . , . , . , . ,
. , . , . , . , . )
IPARM = (1, 3, 0, 1)
RPARM = (1.D-12, 0.1D0)
A = (0.5, . , 0.3, 1.0, . , 1.0, . , 3.0, . , . , . , 1.0,
1.0, . , . , . , . , . , . , . , -1.7, -0.5, -1.0, -1.0,
4.0, -3.0, -4.0)
IA = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, . , . , . , . ,
. , . , . , 2, 1, 1, 3, 3, 5, 5)
JA = (1, 0, 5, 2, 0, 4, 0, 2, 0, 0, 0, 3, 4, . , . , . , . ,
. , . , . , 4, 2, 4, 4, 1, 3, 1)
OPARM = (1.000000, 0.333333, 3.000000)
This subroutine solves either of the following systems:
where A is a sparse matrix, AT is the transpose of sparse matrix A, and x and b are vectors. DGSS uses the results of the factorization of matrix A, produced by a preceding call to DGSF.
| Note: | The input to this solve subroutine must be the output from the factorization subroutine, DGSF. |
| Fortran | CALL DGSS (jopt, n, a, ia, ja, lna, bx, aux, naux) |
| C and C++ | dgss (jopt, n, a, ia, ja, lna, bx, aux, naux); |
| PL/I | CALL DGSS (jopt, n, a, ia, ja, lna, bx, aux, naux); |
If jopt = 0, Ax = b is solved, where the right-hand side is not sparse.
If jopt = 1, ATx = b is solved, where the right-hand side is not sparse.
If jopt = 10, Ax = b is solved, where the right-hand side is sparse.
If jopt = 11, ATx = b is solved, where the right-hand side is sparse.
Specified as: a fullword integer; jopt = 0, 1, 10, or 11.
The system Ax = b is solved for x, where A is a sparse matrix and x and b are vectors. Depending on the value specified for the jopt argument, DGSS can also solve the system ATx = b, where AT is the transpose of sparse matrix A.
If the value specified for the jopt argument is 0 or 10, the following equation is solved:
If the value specified for the jopt argument is 1 or 11, the following equation is solved:
DGSS uses the results of the factorization of matrix A, produced by a preceding call to DGSF. The transformed matrix A consists of the upper triangular matrix U and the lower triangular matrix L.
See references [10], [47], and [87].
None
This example shows how to solve the system Ax = b, where matrix A is a 5 by 5 sparse matrix. The right-hand side is not sparse.
| Note: | The input for this subroutine is the same as the output from DGSF, except for BX. |
* *
| 2.0 0.0 4.0 0.0 0.0 |
| 1.0 1.0 0.0 0.0 3.0 |
| 0.0 0.0 3.0 4.0 0.0 |
| 2.0 2.0 0.0 1.0 5.0 |
| 0.0 0.0 1.0 1.0 0.0 |
* *
JOPT N A IA JA LNA BX AUX NAUX
| | | | | | | | |
CALL DGSS( 0 , 5 , A , IA , JA , 27 , BX , AUX , 150 )
A = (0.5, . , 0.3, 1.0, . , 1.0, . , 3.0, . , . , . , 1.0,
1.0, . , . , . , . , . , . , . , -1.7, -0.5, -1.0, -1.0,
4.0, -3.0, -4.0)
IA = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, . , . , . , . ,
. , . , . , 2, 1, 1, 3, 3, 5, 5)
JA = (1, 0, 5, 2, 0, 4, 0, 2, 0, 0, 0, 3, 4, . , . , . , . ,
. , . , . , 4, 2, 4, 4, 1, 3, 1)
BX = (1.0, 1.0, 1.0, 1.0, 1.0)
IA = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, . , . , . , . ,
. , . , . , 2, 1, 1, 3, 3, 5, 5)
BX = (-5.500000, 9.500000, 3.000000, -2.000000, -1.000000)
This example shows how to solve the system ATx = b, using the same matrix A used in Example 1. The input is also the same as in Example 1, except for the jopt argument. The right-hand side is not sparse.
JOPT N A IA JA LNA BX AUX NAUX
| | | | | | | | |
CALL DGSS( 1 , 5 , A , IA , JA , 27 , BX , AUX , 150 )
BX = (1.0, 1.0, 1.0, 1.0, 1.0)
IA = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, . , . , . , . ,
. , . , . , 2, 1, 1, 3, 3, 5, 5)
BX = (0.000000, -3.000000, -2.000000, 2.000000, 7.000000)
This example shows how to solve the system Ax = b, using the same matrix A as in Examples 1 and 2. The input is also the same as in Examples 1 and 2, except for the jopt and bx arguments. The right-hand side is sparse.
JOPT N A IA JA LNA BX AUX NAUX
| | | | | | | | |
CALL DGSS( 10 , 5 , A , IA , JA , 27 , BX , AUX , 150 )
BX = (0.0, 0.0, 0.0, 1.0, 0.0)
IA = (1, 4, 2, 5, 3, 5, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 2, 1, 1, 3, 3, 5, 5)
BX = (0.000000, 3.000000, 0.000000, 0.000000, -1.000000)
This example shows how to solve the system ATx = b, using the same matrix A as in Examples 1, 2, and 3. The input is also the same as in Examples 1, 2, and 3, except for the jopt argument. The right-hand side is sparse.
JOPT N A IA JA LNA BX AUX NAUX
| | | | | | | | |
CALL DGSS( 11 , 5 , A , IA , JA , 27 , BX , AUX , 150 )
BX = (0.0, 0.0, 0.0, 1.0, 0.0)
IA = (1, 4, 2, 5, 3, 5, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 2, 1, 1, 3, 3, 5, 5)
BX = (0.000000, 0.000000, 1.000000, 0.000000, -3.000000 )
This subroutine can perform either or both of the following functions for general sparse matrix A, stored in skyline storage mode, and for vectors x and b:
You also have the choice of using profile-in or diagonal-out skyline storage mode for A on input or output.
| Note: | The input to the solve performed by this subroutine must be the output from the factorization performed by this subroutine. |
| Fortran | CALL DGKFS (n, au, nu, idu, al, nl, idl, iparm, rparm, aux, naux, bx, ldbx, mbx) |
| C and C++ | dgkfs (n, au, nu, idu, al, nl, idl, iparm, rparm, aux, naux, bx, ldbx, mbx); |
| PL/I | CALL DGKFS (n, au, nu, idu, al, nl, idl, iparm, rparm, aux, naux, bx, ldbx, mbx); |
In each case:
If IPARM(4) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(4) = 1, profile-in skyline storage mode is used for A.
Specified as: a one-dimensional array of (at least) length nu, containing long-precision real numbers.
| Note: | In all these cases, entries in AL for diagonal elements of A are not assumed to have meaningful values. |
In each case:
If IPARM(4) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(4) = 1, profile-in skyline storage mode is used for A.
Specified as: a one-dimensional array of (at least) length nl, containing long-precision real numbers.
If IPARM(1) = 0, the following default values are used. For restrictions, see "Notes".
If IPARM(1) = 1, the default values are not used.
| Type of Computation | Ax = b | Ax = b and Determinant(A) | ATx = b | ATx = b and Determinant(A) |
|---|---|---|---|---|
| Factor and Solve | 0 | 10 | 100 | 110 |
| Factor Only | 1 | 11 | N/A | N/A |
| Solve Only | 2 | N/A | 102 | N/A |
If IPARM(3) = 0, and:
If IPARM(3) > 0, and you are doing a factor only, then a partial factorization is performed on matrix A. Rows 1 through IPARM(3) of columns 1 through IPARM(3) in matrix A must be in factored form from a preceding call to this subroutine. The factorization is performed on rows IPARM(3)+1 through n and columns IPARM(3)+1 through n. For an illustration, see "Notes".
If IPARM(4) = 0, diagonal-out skyline storage mode is used.
If IPARM(4) = 1, profile-in skyline storage mode is used.
If IPARM(5) = 0, diagonal-out skyline storage mode is used.
If IPARM(5) = 1, profile-in skyline storage mode is used.
If you are doing a factor and solve or a factor only, then IPARM(10) indicates whether certain default values for iparm and rparm are used by this subroutine, where:
If you are doing a solve only, this argument is not used.
If you are doing a factor and solve or a factor only, then IPARM(11) through IPARM(15) control the type of processing to apply to pivot elements occurring in regions 1 through 5, respectively. The pivot elements are ukk for k = 1, n when doing a full factorization, and they are k = IPARM(3)+1, n when doing a partial factorization. The region in which a pivot element falls depends on the sign and magnitude of the pivot element. The regions are determined by RPARM(10). For a description of the regions and associated pivot values, see "Notes". For each region i for i = 1,5, where the pivot occurs in region i, the processing applied to the pivot element is determined by IPARM(10+i), where:
| Note: | A value of 0 is not permitted for region 3, because if processing continues, a divide-by-zero exception occurs. |
If you are doing a solve only, these arguments are not used.
Specified as: a one-dimensional array of (at least) length 25, containing fullword integers, where:
If you are doing a factor and solve or a factor only, RPARM(10) is the tolerance value for small pivots. This sets the bounds for the pivot regions, where pivots are processed according to the options you specify for the five regions in IPARM(11) through IPARM(15), respectively. The suggested value is 10-15 <= IPARM(10) <= 1.
If you are doing a solve only, this argument is not used.
If you are doing a factor and solve or a factor only, RPARM(11) through RPARM(15) are the fix-up values to use for the pivots in regions 1 through 5, respectively. For each RPARM(10+i) for i = 1,5, where the pivot occurs in region i:
If you are doing a solve only, these arguments are not used.
Specified as: a one-dimensional array of (at least) length 25, containing long-precision real numbers, where if IPARM(2) = 0, 1, 10, 11, 100, or 110, then:
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing long-precision real numbers.
If naux = 0 and error 2015 is unrecoverable, DGKFS dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise,
If you are doing a factor only, use naux >= 5n.
If you are doing a factor and solve or a solve only, use naux >= 5n+4mbx.
If you are doing a factor and solve or a solve only, bx is the array, containing the mbx right-hand side vectors b of the system Ax = b or ATx = b. Each vector b is length n and is stored in the corresponding column of the array.
If you are doing a factor only, this argument is not used in the computation.
Specified as: an ldbx by (at least) mbx array, containing long-precision real numbers.
If you are doing a factor and solve or a solve only, ldbx is the leading dimension of the array specified for bx.
If you are doing a factor only, this argument is not used in the computation.
Specified as: a fullword integer; ldbx >= n and:
If mbx <> 0, then ldbx > 0.
If mbx = 0, then ldbx >= 0.
If you are doing a factor and solve or a solve only, mbx is the number of right-hand side vectors, b, in the array specified for bx.
If you are doing a factor only, this argument is not used in the computation.
Specified as: a fullword integer; mbx >= 0.
If IPARM(5) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(5) = 1, profile-in skyline storage mode is used for A.
(If mbx = 0 and you are doing a solve only, then au is unchanged on output.) Returned as: a one-dimensional array of (at least) length nu, containing long-precision real numbers.
If IPARM(5) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(5) = 1, profile-in skyline storage mode is used for A.
| Note: | You should assume that entries in AL for diagonal elements of A do not have meaningful values. |
(If mbx = 0 and you are doing a solve only, then al is unchanged on output.) Returned as: a one-dimensional array of (at least) length nl, containing long-precision real numbers.
If you are doing a factor and solve or a factor only, and:
If you are doing a solve only, this argument is not used in the computation and is unchanged.
If you are doing a factor and solve or a factor only, IPARM(21) through IPARM(25) have the following meanings for each region i for i = 1,5, respectively:
If you are doing a solve only, these arguments are not used in the computation and are unchanged.
Returned as: a one-dimensional array of (at least) length 25, containing fullword integers.
If you are doing a factor and solve or a factor only, and:
If you are doing a solve only, this argument is not used in the computation and is unchanged.
If you are computing the determinant of matrix A, then RPARM(17) is the mantissa, detbas, and RPARM(18) is the power of 10, detpwr, used to express the value of the determinant: detbas(10detpwr), where 1 <= detbas < 10. Also:
If you are not computing the determinant of matrix A, these arguments are not used in the computation and are unchanged.
If you are doing a factor and solve or a solve only, bx is the array, containing the mbx solution vectors x of the system Ax = b or ATx = b. Each vector x is length n and is stored in the corresponding column of the array. (If mbx = 0, then bx is unchanged on output.)
If you are doing a factor only, this argument is not used in the computation and is unchanged.
Returned as: an ldbx by (at least) mbx array, containing long-precision real numbers.
 |
For a description of how sparse matrices are stored in skyline storage mode, see "Profile-In Skyline Storage Mode" and "Diagonal-Out Skyline Storage Mode".
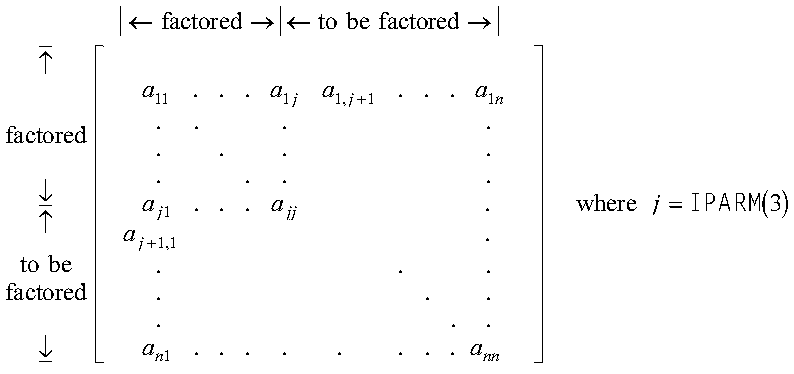
You use the partial factorization function when, for design or storage reasons, you must factor the matrix A in stages. When doing a partial factorization, you must use the same skyline storage mode for all parts of the matrix as it is progressively factored.
This subroutine can factor, compute the determinant of, and solve general sparse matrix A, stored in skyline storage mode. For all computations, input matrix A can be stored in either diagonal-out or profile-in skyline storage mode. Output matrix A can also be stored in either of these modes and can be different from the mode used for input.
Matrix A is factored into the following form using specified pivot processing:
where:
The transformed matrix A, factored into its LU form, is stored in packed format in arrays AU and AL. The inverse of the diagonal of matrix U is stored in the corresponding elements of array AU. The off-diagonal elements of the upper triangular matrix U are stored in the corresponding off-diagonal elements of array AU. The off-diagonal elements of the lower triangular matrix L are stored in the corresponding off-diagonal elements of array AL. (The diagonal elements stored in array AL do not have meaningful values.)
The partial factorization of matrix A, which you can do when you specify the factor-only option, assumes that the first IPARM(3) rows and columns are already factored in the input matrix. It factors the remaining n-IPARM(3) rows and columns in matrix A. (See "Notes" for an illustration.) It updates only the elements in arrays AU and AL corresponding to the part of matrix A that is factored.
The determinant can be computed with any of the factorization computations. With a full factorization, you get the determinant for the whole matrix. With a partial factorization, you get the determinant for only that part of the matrix factored in this computation.
The system Ax = b or ATx = b, having multiple right-hand sides, is solved for x, using the transformed matrix A produced by this call or a subsequent call to this subroutine.
See references [9], [12], [25], [47], and [65]. If n is 0, no computation is performed. If mbx is 0, no solve is performed.
This example shows how to factor a 9 by 9 general sparse matrix A and solve the system Ax = b with three right-hand sides. The default values are used for IPARM and RPARM. Input matrix A, shown here, is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| 2.0 2.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 2.0 4.0 4.0 2.0 2.0 0.0 0.0 0.0 2.0 |
| 2.0 4.0 6.0 4.0 4.0 0.0 2.0 0.0 4.0 |
| 2.0 4.0 6.0 6.0 6.0 2.0 4.0 0.0 6.0 |
| 0.0 0.0 0.0 2.0 4.0 4.0 4.0 2.0 4.0 |
| 0.0 2.0 4.0 6.0 8.0 6.0 8.0 4.0 10.0 |
| 0.0 0.0 0.0 2.0 4.0 6.0 8.0 6.0 8.0 |
| 0.0 0.0 0.0 2.0 4.0 6.0 8.0 8.0 10.0 |
| 2.0 4.0 6.0 6.0 8.0 6.0 10.0 8.0 16.0 |
* *
Output matrix A, shown here, is in LU factored form with U-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix B is:
* *
| 0.5 2.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 0.5 2.0 2.0 2.0 0.0 0.0 0.0 2.0 |
| 1.0 1.0 0.5 2.0 2.0 0.0 2.0 0.0 2.0 |
| 1.0 1.0 1.0 0.5 2.0 2.0 2.0 0.0 2.0 |
| 0.0 0.0 0.0 1.0 0.5 2.0 2.0 2.0 2.0 |
| 0.0 1.0 1.0 1.0 1.0 0.5 2.0 2.0 2.0 |
| 0.0 0.0 0.0 1.0 1.0 1.0 0.5 2.0 2.0 |
| 0.0 0.0 0.0 1.0 1.0 1.0 1.0 0.5 2.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.5 |
* *
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | | |
CALL DGKFS( 9 , AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 57 , BX , 12 , 3 )
AU = (2.0, 4.0, 2.0, 6.0, 4.0, 2.0, 6.0, 4.0, 2.0, 4.0, 6.0,
4.0, 2.0, 6.0, 4.0, 2.0, 8.0, 8.0, 4.0, 4.0, 2.0, 8.0,
6.0, 4.0, 2.0, 16.0, 10.0, 8.0, 10.0, 4.0, 6.0, 4.0, 2.0)
IDU = (1, 2, 4, 7, 10, 14, 17, 22, 26, 34)
AL = (0.0, 0.0, 2.0, 0.0, 4.0, 2.0, 0.0, 6.0, 4.0, 2.0, 0.0,
2.0, 0.0, 8.0, 6.0, 4.0, 2.0, 0.0, 6.0, 4.0, 2.0, 0.0,
8.0, 6.0, 4.0, 2.0, 0.0, 8.0, 10.0, 6.0, 8.0, 6.0, 6.0,
4.0, 2.0)
IDL = (1, 2, 4, 7, 11, 13, 18, 22, 27, 36)
IPARM = (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
* *
| 6.00 12.00 18.00 |
| 16.00 32.00 48.00 |
| 26.00 52.00 78.00 |
| 36.00 72.00 108.00 |
| 20.00 40.00 60.00 |
BX = | 48.00 96.00 144.00 |
| 34.00 68.00 102.00 |
| 38.00 76.00 114.00 |
| 66.00 132.00 198.00 |
| . . . |
| . . . |
| . . . |
* *
AU = (0.5, 0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 0.5,
2.0, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0)
IDL =(same as input)
IPARM = (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 9, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, . , . , . , . , . , . , . , . , . )
* *
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
BX = | 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| . . . |
| . . . |
| . . . |
* *
This example shows how to factor the 9 by 9 general sparse matrix A from Example 1, solve the system ATx = b with three right-hand sides, and compute the determinant of A. The default values for pivot processing are used for IPARM. Input matrix A is stored in profile-in skyline storage mode. Output matrix A is in LU factored form with U-1 on the diagonal, and is stored in diagonal-out skyline storage mode. It is the same as output matrix A in Example 1.
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | &darrow |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 57 , BX , 12 , 3 )
AU = (2.0, 2.0, 4.0, 2.0, 4.0, 6.0, 2.0, 4.0, 6.0, 2.0, 4.0,
6.0, 4.0, 2.0, 4.0, 6.0, 2.0, 4.0, 4.0, 8.0, 8.0, 2.0,
4.0, 6.0, 8.0, 2.0, 4.0, 6.0, 4.0, 10.0, 8.0, 10.0, 16.0)
IDU = (1, 3, 6, 9, 13, 16, 21, 25, 33, 34)
AL = (0.0, 2.0, 0.0, 2.0, 4.0, 0.0, 2.0, 4.0, 6.0, 0.0, 2.0,
0.0, 2.0, 4.0, 6.0, 8.0, 0.0, 2.0, 4.0, 6.0, 0.0, 2.0,
4.0, 6.0, 8.0, 0.0, 2.0, 4.0, 6.0, 6.0, 8.0, 6.0, 10.0,
8.0, 0.0)
IDL = (1, 3, 6, 10, 12, 17, 21, 26, 35, 36)
IPARM = (1, 110, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
* *
| 10.00 20.00 30.00 |
| 20.00 40.00 60.00 |
| 28.00 56.00 84.00 |
| 30.00 60.00 90.00 |
| 40.00 80.00 120.00 |
BX = | 30.00 60.00 90.00 |
| 44.00 88.00 132.00 |
| 28.00 56.00 84.00 |
| 60.00 120.00 180.00 |
| . . . |
| . . . |
| . . . |
* *
AU =(same as output AU in Example 1)
IDU =(same as output IDU in Example 1)
AL =(same as output AL in Example 1)
IDL =(same as output IDL in Example 1)
IPARM = (1, 110, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . ,
9, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, 5.12, 2.0, . , . , . , . , . , . , . )
BX =(same as output BX in Example 1)
This example shows how to factor a 9 by 9 negative-definite general sparse matrix A, solve the system Ax = b with three right-hand sides, and compute the determinant of A. (Default values for pivot processing are not used for IPARM because A is negative-definite.) Input matrix A, shown here, is stored in diagonal-out skyline storage mode:
* *
| -2.0 -2.0 -2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| -2.0 -4.0 -4.0 -2.0 -2.0 0.0 0.0 0.0 -2.0 |
| -2.0 -4.0 -6.0 -4.0 -4.0 0.0 -2.0 0.0 -4.0 |
| -2.0 -4.0 -6.0 -6.0 -6.0 -2.0 -4.0 0.0 -6.0 |
| 0.0 0.0 0.0 -2.0 -4.0 -4.0 -4.0 -2.0 -4.0 |
| 0.0 -2.0 -4.0 -6.0 -8.0 -6.0 -8.0 -4.0 -10.0 |
| 0.0 0.0 0.0 -2.0 -4.0 -6.0 -8.0 -6.0 -8.0 |
| 0.0 0.0 0.0 -2.0 -4.0 -6.0 -8.0 -8.0 -10.0 |
| -2.0 -4.0 -6.0 -6.0 -8.0 -6.0 -10.0 -8.0 -16.0 |
* *
Output matrix A, shown here, is in LU factored form with U-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| -0.5 -2.0 -2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 -0.5 -2.0 -2.0 -2.0 0.0 0.0 0.0 -2.0 |
| 1.0 1.0 -0.5 -2.0 -2.0 0.0 -2.0 0.0 -2.0 |
| 1.0 1.0 1.0 -0.5 -2.0 -2.0 -2.0 0.0 -2.0 |
| 0.0 0.0 0.0 1.0 -0.5 -2.0 -2.0 -2.0 -2.0 |
| 0.0 1.0 1.0 1.0 1.0 -0.5 -2.0 -2.0 -2.0 |
| 0.0 0.0 0.0 1.0 1.0 1.0 -0.5 -2.0 -2.0 |
| 0.0 0.0 0.0 1.0 1.0 1.0 1.0 -0.5 -2.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 -0.5 |
* *
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | | |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 57 , BX , 12 , 3 )
AU = (-2.0, -4.0, -2.0, -6.0, -4.0, -2.0, -6.0, -4.0, -2.0,
-4.0, -6.0, -4.0, -2.0, -6.0, -4.0, -2.0, -8.0, -8.0,
-4.0, -4.0, -2.0, -8.0, -6.0, -4.0, -2.0, -16.0, -10.0,
-8.0, -10.0, -4.0, -6.0, -4.0, -2.0)
IDU = (1, 2, 4, 7, 10, 14, 17, 22, 26, 34)
AL = (0.0, 0.0, -2.0, 0.0, -4.0, -2.0, 0.0, -6.0, -4.0, -2.0,
0.0, -2.0, 0.0, -8.0, -6.0, -4.0, -2.0, 0.0, -6.0, -4.0,
-2.0, 0.0, -8.0, -6.0, -4.0, -2.0, 0.0, -8.0, -10.0,
-6.0, -8.0, -6.0, -6.0, -4.0, -2.0)
IDL = (1, 2, 4, 7, 11, 13, 18, 22, 27, 36)
IPARM = (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, . ,
. , . , . , . , . , . , . , . , . )
RPARM = ( . , . , . , . , . , . , . , . , . , 10-15, . , . ,
. , . , . , . , . , . , . , . , . , . , . , . , . )
BX =(same as input BX in Example 1)
AU = (-0.5, -0.5, -2.0, -0.5, -2.0, -2.0, -0.5, -2.0, -2.0,
-0.5, -2.0, -2.0, -2.0, -0.5, -2.0, -2.0, -0.5, -2.0,
-2.0, -2.0, -2.0, -0.5, -2.0, -2.0, -2.0, -0.5, -2.0,
-2.0, -2.0, -2.0, -2.0, -2.0, -2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0)
IDL =(same as input)
IPARM = (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, 9,
. , . , . , . , 9, 0, 0, 0, 0)
RPARM = ( . , . , . , . , . , . , . , . , . , 10-15, . , . ,
. , . , . , 8.0, -5.12, 2.0, . , . , . , . , . , . , . )
* *
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
BX = | -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| . . . |
| . . . |
| . . . |
* *
This example shows how to factor the first six rows and columns, referred to as matrix A1, of the 9 by 9 general sparse matrix A from Example 1 and compute the determinant of A1. Input matrix A1, shown here, is stored in diagonal-out skyline storage mode. Input matrix A1 is:
* *
| 2.0 2.0 2.0 0.0 0.0 0.0 |
| 2.0 4.0 4.0 2.0 2.0 0.0 |
| 2.0 4.0 6.0 4.0 4.0 0.0 |
| 2.0 4.0 6.0 6.0 6.0 2.0 |
| 0.0 0.0 0.0 2.0 4.0 4.0 |
| 0.0 2.0 4.0 6.0 8.0 6.0 |
* *
Output matrix A1, shown here, is in LU factored form with U-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Output matrix A1 is:
* *
| 0.5 2.0 2.0 0.0 0.0 0.0 |
| 1.0 0.5 2.0 2.0 2.0 0.0 |
| 1.0 1.0 0.5 2.0 2.0 0.0 |
| 1.0 1.0 1.0 0.5 2.0 2.0 |
| 0.0 0.0 0.0 1.0 0.5 2.0 |
| 0.0 1.0 1.0 1.0 1.0 0.5 |
* *
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | | |
CALL DGKFS( 6, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 45 , BX , LDBX , MBX )
AU =(same as input AU in Example 1)
IDU = (1, 2, 4, 7, 10, 14, 17)
AL =(same as input AL in Example 1)
IDL = (1, 2, 4, 7, 11, 13, 18)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)
AU = (0.5, 0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 8.0, 8.0, 4.0, 4.0, 2.0, 8.0,
6.0, 4.0, 2.0, 16.0, 10.0, 8.0, 10.0, 4.0, 6.0, 4.0, 2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 6.0, 4.0, 2.0, 0.0,
8.0, 6.0, 4.0, 2.0, 0.0, 8.0, 10.0, 6.0, 8.0, 6.0, 6.0,
4.0, 2.0)
IDL =(same as input)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . , 3,
. , . , . , . , 0, 0, 0, 0, 6)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 3.0, 6.4, 1.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)
This example shows how to do a partial factorization of the 9 by 9 general sparse matrix A from Example 1, where the first six rows and columns were factored in Example 4. It factors the remaining three rows and columns and computes the determinant of that part of the matrix. The input matrix, referred to as A2, shown here, is made up of the output factored matrix A1 plus the three remaining unfactored rows and columns of matrix A. Matrix A2 is:
* *
| 0.5 2.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 0.5 2.0 2.0 2.0 0.0 0.0 0.0 2.0 |
| 1.0 1.0 0.5 2.0 2.0 0.0 2.0 0.0 4.0 |
| 1.0 1.0 1.0 0.5 2.0 2.0 4.0 0.0 6.0 |
| 0.0 0.0 0.0 1.0 0.5 2.0 4.0 2.0 4.0 |
| 0.0 1.0 1.0 1.0 1.0 0.5 8.0 4.0 10.0 |
| 0.0 0.0 0.0 2.0 4.0 6.0 8.0 6.0 8.0 |
| 0.0 0.0 0.0 2.0 4.0 6.0 8.0 8.0 10.0 |
| 2.0 4.0 6.0 6.0 8.0 6.0 10.0 8.0 16.0 |
* *
Both parts of input matrix A2 are stored in diagonal-out skyline storage mode.
Output matrix A2 is the same as output matrix A in Example 1 and is stored in diagonal-out skyline storage mode.
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | | |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 45 , BX , LDBX , MBX )
AU =(same as output AU in Example 4)
IDU =(same as input IDU in Example 1)
AL =(same as output AL in Example 4)
IDL =(same as input IDL in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)
AU =(same as output AU in Example 1)
IDU =(same as output IDU in Example 1)
AL =(same as output AL in Example 1)
IDL =(same as output IDL in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . , 9,
. , . , . , . , 0, 0, 0, 0, 3)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, 8.0, 0.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)
This example shows how to solve the system Ax = b with one right-hand side for a general sparse matrix A. Input matrix A, used here, is the same as factored output matrix A from Example 1, stored in profile-in skyline storage mode. Here, output matrix A is unchanged on output and is stored in profile-in skyline storage mode.
N AU NU IDU AL NL IDL IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | | | | |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 49 , BX , 9 , 1 )
AU = (0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0,
2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 0.5)
IDU = (1, 3, 6, 9, 13, 16, 21, 25, 33, 34)
AL = (0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 1.0,
0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 1.0,
1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 0.0)
IDL = (1, 3, 6, 10, 12, 17, 21, 26, 35, 36)
IPARM = (1, 2, 0, 1, 1, . , . , . , . , . , . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX = (12.0, 58.0, 114.0, 176.0, 132.0, 294.0, 240.0, 274.0,
406.0)
AU =(same as input) IDU =(same as input) AL =(same as input) IDL =(same as input) IPARM =(same as input) RPARM =(not relevant) BX = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0)
This subroutine can perform either or both of the following functions for symmetric sparse matrix A, stored in skyline storage mode, and for vectors x and b:
You have the choice of using either Gaussian elimination or Cholesky decomposition. You also have the choice of using profile-in or diagonal-out skyline storage mode for A on input or output.
| Note: | The input to the solve performed by this subroutine must be the output from the factorization performed by this subroutine. |
| Fortran | CALL DSKFS (n, a, na, idiag, iparm, rparm, aux, naux, bx, ldbx, mbx) |
| C and C++ | dskfs (n, a, na, idiag, iparm, rparm, aux, naux, bx, ldbx, mbx); |
| PL/I | CALL DSKFS (n, a, na, idiag, iparm, rparm, aux, naux, bx, ldbx, mbx); |
In each case:
If IPARM(4) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(4) = 1, profile-in skyline storage mode is used for A.
Specified as: a one-dimensional array of (at least) length na, containing long-precision real numbers.
If IPARM(1) = 0, the following default values are used. For restrictions, see "Notes".
If IPARM(1) = 1, the default values are not used.
| Type of Computation | Gaussian Elimination Ax = b | Gaussian Elimination Ax = b and Determinant(A) | Cholesky Decomposition Ax = b | Cholesky Decomposition Ax = b and Determinant(A) |
|---|---|---|---|---|
| Factor and Solve | 0 | 10 | 100 | 110 |
| Factor Only | 1 | 11 | 101 | 111 |
| Solve Only | 2 | N/A | 102 | N/A |
If IPARM(3) = 0, and:
If IPARM(3) > 0, and you are doing a factor only, then a partial factorization is performed on matrix A. Rows 1 through IPARM(3) of columns 1 through IPARM(3) in matrix A must be in factored form from a preceding call to this subroutine. The factorization is performed on rows IPARM(3)+1 through n and columns IPARM(3)+1 through n. For an illustration, see "Notes".
If IPARM(4) = 0, diagonal-out skyline storage mode is used.
If IPARM(4) = 1, profile-in skyline storage mode is used.
If IPARM(5) = 0, diagonal-out skyline storage mode is used.
If IPARM(5) = 1, profile-in skyline storage mode is used.
If you are doing a factor and solve or a factor only, then IPARM(10) indicates whether certain default values for iparm and rparm are used by this subroutine, where:
If you are doing a solve only, this argument is not used.
If you are doing a factor and solve or a factor only, then IPARM(11) through IPARM(15) control the type of processing to apply to pivot elements occurring in regions 1 through 5, respectively. The pivot elements are dkk for Gaussian elimination and rkk for Cholesky decomposition for k = 1, n when doing a full factorization, and they are k = IPARM(3)+1, n when doing a partial factorization. The region in which a pivot element falls depends on the sign and magnitude of the pivot element. The regions are determined by RPARM(10). For a description of the regions and associated pivot values, see "Notes". For each region i for i = 1,5, where the pivot occurs in region i, the processing applied to the pivot element is determined by IPARM(10+i), where:
| Note: | A value of 0 is not permitted for region 3, because if processing continues, a divide-by-zero exception occurs. In addition, if you are doing a Cholesky decomposition, a value of 0 is not permitted in regions 1 and 2, because a square root exception occurs. |
If you are doing a solve only, these arguments are not used.
Specified as: a one-dimensional array of (at least) length 25, containing fullword integers, where:
If IPARM(2) = 100, 101, 110, or 111, then:
If you are doing a factor and solve or a factor only, RPARM(10) is the tolerance value for small pivots. This sets the bounds for the pivot regions, where pivots are processed according to the options you specify for the five regions in IPARM(11) through IPARM(15), respectively. The suggested value is 10-15 <= IPARM(10) <= 1.
If you are doing a solve only, this argument is not used.
If you are doing a factor and solve or a factor only, RPARM(11) through RPARM(15) are the fix-up values to use for the pivots in regions 1 through 5, respectively. For each RPARM(10+i) for i = 1,5, where the pivot occurs in region i:
If you are doing a solve only, these arguments are not used.
Specified as: a one-dimensional array of (at least) length 25, containing long-precision real numbers, where if IPARM(2) = 0, 1, 10, 11, 100, 101, 110, or 111, then:
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing long-precision real numbers.
If naux = 0 and error 2015 is unrecoverable, DSKFS dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, If you are doing a factor only, you can use naux >= n; however, for optimal performance, use naux >= 3n.
If you are doing a factor and solve or a solve only, use naux >= 3n+4mbx.
For further details on error handling and the special factor-only case, see "Notes".
If you are doing a factor and solve or a solve only, bx is the array, containing the mbx right-hand side vectors b of the system Ax = b. Each vector b is length n and is stored in the corresponding column of the array.
If you are doing a factor only, this argument is not used in the computation.
Specified as: an ldbx by (at least) mbx array, containing long-precision real numbers.
If you are doing a factor and solve or a solve only, ldbx is the leading dimension of the array specified for bx.
If you are doing a factor only, this argument is not used in the computation.
Specified as: a fullword integer; ldbx >= n and:
If mbx <> 0, then ldbx > 0.
If mbx = 0, then ldbx >= 0.
If you are doing a factor and solve or a solve only, mbx is the number of right-hand side vectors, b, in the array specified for bx.
If you are doing a factor only, this argument is not used in the computation.
Specified as: a fullword integer; mbx >= 0.
If IPARM(5) = 0, diagonal-out skyline storage mode is used for A.
If IPARM(5) = 1, profile-in skyline storage mode is used for A.
(If mbx = 0 and you are doing a solve only, then a is unchanged on output.) Returned as: a one-dimensional array of (at least) length na, containing long-precision real numbers.
Returned as: a one-dimensional array of (at least) length n+1, containing fullword integers.
If you are doing a factor and solve or a factor only, and:
If you are doing a solve only, this argument is not used in the computation and is unchanged.
If you are doing a factor and solve or a factor only, IPARM(21) through IPARM(25) have the following meanings for each region i for i = 1,5, respectively:
If you are doing a solve only, these arguments are not used in the computation and are unchanged.
Returned as: a one-dimensional array of (at least) length 25, containing fullword integers.
If you are doing a factor and solve or a factor only, and:
If you are doing a solve only, this argument is not used in the computation and is unchanged.
If you are computing the determinant of matrix A, then RPARM(17) is the mantissa, detbas, and RPARM(18) is the power of 10, detpwr, used to express the value of the determinant: detbas(10detpwr), where 1 <= detbas < 10. Also:
If you are not computing the determinant of matrix A, these arguments are not used in the computation and are unchanged.
If you are doing a factor and solve or a solve only, bx is the array, containing the mbx solution vectors x of the system Ax = b. Each vector x is length n and is stored in the corresponding column of the array. (If mbx = 0, then bx is unchanged on output.)
If you are doing a factor only, this argument is not used in the computation and is unchanged.
Returned as: an ldbx by (at least) mbx array, containing long-precision real numbers.
 |
For a description of how sparse matrices are stored in skyline storage
mode, see "Profile-In Skyline Storage Mode" and "Diagonal-Out Skyline Storage Mode". Those descriptions use different array and variable names from the ones
used here. To relate the two sets, use the following table:
| Name Here | Name in the Storage Description |
|---|---|
| A | AU |
| na | nu |
| IDIAG | IDU |
You use the partial factorization function when, for design or storage reasons, you must factor the matrix A in stages. When doing a partial factorization, you must use the same skyline storage mode for all parts of the matrix as it is progressively factored.
This subroutine can factor, compute the determinant of, and solve symmetric sparse matrix A, stored in skyline storage mode. It can use either Gaussian elimination or Cholesky decomposition. For all computations, input matrix A can be stored in either diagonal-out or profile-in skyline storage mode. Output matrix A can also be stored in either of these modes and can be different from the mode used for input.
For Gaussian elimination, matrix A is factored into the following form using specified pivot processing:
where:
The transformed matrix A, factored into its LDLT form, is stored in packed format in array A, such that the inverse of the diagonal matrix D is stored in the corresponding elements of array A. The off-diagonal elements of the unit upper triangular matrix LT are stored in the corresponding off-diagonal elements of array A.
For Cholesky decomposition, matrix A is factored into the following form using specified pivot processing:
where R is an upper triangular matrix
The transformed matrix A, factored into its RTR form, is stored in packed format in array A, such that the inverse of the diagonal elements of the upper triangular matrix R is stored in the corresponding elements of array A. The off-diagonal elements of matrix R are stored in the corresponding off-diagonal elements of array A.
The partial factorization of matrix A, which you can do when you specify the factor-only option, assumes that the first IPARM(3) rows and columns are already factored in the input matrix. It factors the remaining n-IPARM(3) rows and columns in matrix A. (See "Notes" for an illustration.) It updates only the elements in array A corresponding to the part of matrix A that is factored.
The determinant can be computed with any of the factorization computations. With a full factorization, you get the determinant for the whole matrix. With a partial factorization, you get the determinant for only that part of the matrix factored in this computation.
The system Ax = b, having multiple right-hand sides, is solved for x using the transformed matrix A produced by this call or a subsequent call to this subroutine.
See references [9], [12], [25], [47], [65]. If n is 0, no computation is performed. If mbx is 0, no solve is performed.
This example shows how to factor a 9 by 9 symmetric sparse matrix A and solve the system Ax = b with three right-hand sides. It uses Gaussian elimination. The default values are used for IPARM and RPARM. Input matrix A, shown here, is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 2.0 2.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 2.0 3.0 3.0 2.0 2.0 0.0 2.0 0.0 |
| 1.0 2.0 3.0 4.0 3.0 3.0 0.0 3.0 0.0 |
| 0.0 1.0 2.0 3.0 4.0 4.0 1.0 4.0 0.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 2.0 5.0 1.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 3.0 3.0 2.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 3.0 7.0 3.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 3.0 4.0 |
* *
Output matrix A, shown here, is in LDLT factored form with D-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 1.0 |
* *
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS( 9, A, 33, IDIAG, IPARM, RPARM, AUX, 39 , BX , 12 , 3 )
A = (1.0, 2.0, 1.0, 3.0, 2.0, 1.0, 4.0, 3.0, 2.0, 1.0, 4.0,
3.0, 2.0, 1.0, 5.0, 4.0, 3.0, 2.0, 1.0, 3.0, 2.0, 1.0,
7.0, 3.0, 5.0, 4.0, 3.0, 2.0, 1.0, 4.0, 3.0, 2.0, 1.0)
IDIAG = (1, 2, 4, 7, 11, 15, 20, 23, 30, 34)
IPARM = (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
* *
| 4.00 8.00 12.00 |
| 10.00 20.00 30.00 |
| 15.00 30.00 45.00 |
| 19.00 38.00 57.00 |
| 19.00 38.00 57.00 |
BX = | 23.00 46.00 69.00 |
| 11.00 22.00 33.00 |
| 28.00 56.00 84.00 |
| 10.00 20.00 30.00 |
| . . . |
| . . . |
| . . . |
* *
A = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
IDIAG =(same as input)
IPARM = (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 7.0, . , . , . , . , . , . , . , . , . )
* *
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
BX = | 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| 1.00 2.00 3.00 |
| . . . |
| . . . |
| . . . |
* *
This example shows how to factor the 9 by 9 symmetric sparse matrix A from Example 1, solve the system Ax = b with three right-hand sides, and compute the determinant of A. It uses Gaussian elimination. The default values for pivot processing are used for IPARM. Input matrix A is stored in profile-in skyline storage mode. Output matrix A is in LDLT factored form with D-1 on the diagonal, and is stored in diagonal-out skyline storage mode. It is the same as output matrix A in Example 1.
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS( 9, A, 33, IDIAG, IPARM, RPARM, AUX, 39 , BX , 12 , 3 )
A = (1.0, 1.0, 2.0, 1.0, 2.0, 3.0, 1.0, 2.0, 3.0, 4.0, 1.0,
2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 5.0, 1.0, 2.0, 3.0,
1.0, 2.0, 3.0, 4.0, 5.0, 3.0, 7.0, 1.0, 2.0, 3.0, 4.0)
IDIAG = (1, 3, 6, 10, 14, 19, 22, 29, 33, 34)
IPARM = (1, 10, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
* *
| 4.00 8.00 12.00 |
| 10.00 20.00 30.00 |
| 15.00 30.00 45.00 |
| 19.00 38.00 57.00 |
| 19.00 38.00 57.00 |
BX = | 23.00 46.00 69.00 |
| 11.00 22.00 33.00 |
| 28.00 56.00 84.00 |
| 10.00 20.00 30.00 |
| . . . |
| . . . |
| . . . |
* *
A =(same as output A in Example 1)
IDIAG =(same as input IDIAG in Example 1)
IPARM = (1, 10, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . , 8,
. , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 7.0, 1.0, 0.0, . , . , . , . , . , . , . )
BX =(same as output BX in Example 1)
This example shows how to factor a 9 by 9 negative-definite symmetric sparse matrix A, solve the system Ax = b with three right-hand sides, and compute the determinant of A. It uses Gaussian elimination. (Default values for pivot processing are not used for IPARM because A is negative-definite.) Input matrix A, shown here, is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| -1.0 -1.0 -1.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| -1.0 -2.0 -2.0 -2.0 -1.0 -1.0 0.0 -1.0 0.0 |
| -1.0 -2.0 -3.0 -3.0 -2.0 -2.0 0.0 -2.0 0.0 |
| -1.0 -2.0 -3.0 -4.0 -3.0 -3.0 0.0 -3.0 0.0 |
| 0.0 -1.0 -2.0 -3.0 -4.0 -4.0 -1.0 -4.0 0.0 |
| 0.0 -1.0 -2.0 -3.0 -4.0 -5.0 -2.0 -5.0 -1.0 |
| 0.0 0.0 0.0 0.0 -1.0 -2.0 -3.0 -3.0 -2.0 |
| 0.0 -1.0 -2.0 -3.0 -4.0 -5.0 -3.0 -7.0 -3.0 |
| 0.0 0.0 0.0 0.0 0.0 -1.0 -2.0 -3.0 -4.0 |
* *
Output matrix A, shown here, is in LDLT factored form with D-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix A is:
* *
| -1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 -1.0 1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 1.0 -1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 1.0 1.0 -1.0 1.0 1.0 0.0 1.0 0.0 |
| 0.0 1.0 1.0 1.0 -1.0 1.0 1.0 1.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 -1.0 1.0 1.0 1.0 |
| 0.0 0.0 0.0 0.0 1.0 1.0 -1.0 1.0 1.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 1.0 -1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 -1.0 |
* *
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS(9, A, 33, IDIAG, IPARM, RPARM, AUX, 39 , BX , 12 , 3 )
A = (-1.0, -2.0, -1.0, -3.0, -2.0, -1.0, -4.0, -3.0, -2.0,
-1.0, -4.0, -3.0, -2.0, -1.0, -5.0, -4.0, -3.0, -2.0,
-1.0, -3.0, -2.0, -1.0, -7.0, -3.0, -5.0, -4.0, -3.0,
-2.0, -1.0, -4.0, -3.0, -2.0, -1.0)
IDIAG = (1, 2, 4, 7, 11, 15, 20, 23, 30, 34)
IPARM = (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, . ,
. , . , . , . , . , . , . , . , . )
RPARM = ( . , . , . , . , . , . , . , . , . , 10-15, . , . ,
. , . , . , . , . , . , . , . , . , . , . , . , . )
BX =(same as input BX in Example 1)
A = (-1.0, -1.0, 1.0, -1.0, 1.0, 1.0, -1.0, 1.0, 1.0, 1.0,
-1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0,
1.0, -1.0 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0,
1.0)
IDIAG =(same as input)
IPARM = (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, 8,
. , . , . , . , 9, 0, 0, 0, 0)
RPARM = ( . , . , . , . , . , . , . , . , . ,10-15, . , . ,
. , . , . , 7.0, -1.0, 0.0, . , . , . , . , . , . , . )
* *
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
BX = | -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| -1.00 -2.00 -3.00 |
| . . . |
| . . . |
| . . . |
* *
This example shows how to factor the first six rows and columns, referred to as matrix A1, of the 9 by 9 symmetric sparse matrix A from Example 1 and compute the determinant of A1. It uses Gaussian elimination. Input matrix A1, shown here, is stored in diagonal-out skyline storage mode. Input matrix A1 is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 |
| 1.0 2.0 2.0 2.0 1.0 1.0 |
| 1.0 2.0 3.0 3.0 2.0 2.0 |
| 1.0 2.0 3.0 4.0 3.0 3.0 |
| 0.0 1.0 2.0 3.0 4.0 4.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 |
* *
Output matrix A1, shown here, is in LDLT factored form with D-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Output matrix A1 is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 |
* *
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS (6 , A , 33 , IDIAG , IPARM , RPARM , AUX , 27 , BX , LDBX , MBX )
A =(same as input A in Example 1)
IDIAG = (1, 2, 4, 7, 11, 15, 20)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)
A = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 3.0, 2.0, 1.0,
7.0, 3.0, 5.0, 4.0, 3.0, 2.0, 1.0, 4.0, 3.0, 2.0, 1.0)
IDIAG =(same as input)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . , 6,
. , . , . , . , 0, 0, 0, 0, 6)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 5.0, 1.0, 0.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)
This example shows how to do a partial factorization of the 9 by 9 symmetric sparse matrix A from Example 1, where the first six rows and columns were factored in Example 4. It factors the remaining three rows and columns and computes the determinant of that part of the matrix. It uses Gaussian elimination. The input matrix, referred to as A2, shown here, is made up of the output factored matrix A1 plus the three remaining unfactored rows and columns of matrix A Matrix A2 is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 1.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 2.0 0.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 0.0 3.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 1.0 4.0 0.0 |
| 0.0 1.0 1.0 1.0 1.0 1.0 2.0 5.0 1.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 3.0 3.0 2.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 3.0 7.0 3.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 3.0 4.0 |
* *
Both parts of input matrix A2 are stored in diagonal-out skyline storage mode.
Output matrix A2 is the same as output matrix A in Example 1 and is stored in diagonal-out skyline storage mode.
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS (9 , A , 33 , IDIAG , IPARM , RPARM , AUX , 27 , BX , LDBX , MBX )
A =(same as output A in Example 4)
IDIAG =(same as input IDIAG in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)
A =(same as output A in Example 1)
IDIAG =(same as output IDIAG in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . , 8,
. , . , . , . , 0, 0, 0, 0, 3)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 7.0, 1.0, 0.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)
This example shows how to solve the system Ax = b with one right-hand side for a symmetric sparse matrix A. Input matrix A, used here, is the same as factored output matrix A from Example 1, stored in profile-in skyline storage mode. It specifies Gaussian elimination, as used in Example 1. Here, output matrix A is unchanged on output and is stored in profile-in skyline storage mode.
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS (9, A, 33, IDIAG, IPARM, RPARM, AUX, 31 , BX , 9 , 1 )
A = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
IDIAG = (1, 3, 6, 10, 14, 19, 22, 29, 33, 34)
IPARM = (1, 2, 0, 1, 1, . , . , . , . , . , . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX = (10.0, 38.0, 64.0, 87.0, 103.0, 133.0, 80.0, 174.0, 80.0)
A =(same as input) IDIAG =(same as input) IPARM =(same as input) APARM =(same as input) BX = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0)
This example shows how to factor a 9 by 9 symmetric sparse matrix A and solve the system Ax = b with four right-hand sides. It uses Cholesky decomposition. Input matrix A, shown here, is stored in profile-in skyline storage mode Matrix A is:
* *
| 1.0 1.0 1.0 0.0 1.0 0.0 0.0 0.0 1.0 |
| 1.0 5.0 3.0 0.0 3.0 0.0 0.0 0.0 3.0 |
| 1.0 3.0 11.0 3.0 5.0 3.0 3.0 0.0 5.0 |
| 0.0 0.0 3.0 17.0 5.0 5.0 5.0 0.0 5.0 |
| 1.0 3.0 5.0 5.0 29.0 7.0 7.0 0.0 9.0 |
| 0.0 0.0 3.0 5.0 7.0 39.0 9.0 6.0 9.0 |
| 0.0 0.0 3.0 5.0 7.0 9.0 53.0 8.0 11.0 |
| 0.0 0.0 0.0 0.0 0.0 6.0 8.0 66.0 10.0 |
| 1.0 3.0 5.0 5.0 9.0 9.0 11.0 10.0 89.0 |
* *
Output matrix A, shown here, is in RTR factored form with the inverse of the diagonal of R on the diagonal, and is stored in profile-in skyline storage mode. Matrix A is:
* *
| 1.0 1.0 1.0 0.0 1.0 0.0 0.0 0.0 1.0 |
| 1.0 .5 1.0 0.0 1.0 0.0 0.0 0.0 1.0 |
| 1.0 1.0 .333 1.0 1.0 1.0 1.0 0.0 1.0 |
| 0.0 0.0 1.0 .25 1.0 1.0 1.0 0.0 1.0 |
| 1.0 1.0 1.0 1.0 .2 1.0 1.0 0.0 1.0 |
| 0.0 0.0 1.0 1.0 1.0 .167 1.0 1.0 1.0 |
| 0.0 0.0 1.0 1.0 1.0 1.0 .143 1.0 1.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 1.0 .125 1.0 |
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 .111 |
* *
N A NA IDIAG IPARM RPARM AUX NAUX BX LDBX MBX
| | | | | | | | | | |
CALL DSKFS( 9, A, 34, IDIAG, IPARM, RPARM, AUX, 43 , BX , 10 , 4 )
A = (1.0, 1.0, 5.0, 1.0, 3.0, 11.0, 3.0, 17.0, 1.0, 3.0, 5.0,
5.0, 29.0, 3.0, 5.0, 7.0, 39.0, 3.0, 5.0, 7.0, 9.0, 53.0,
6.0, 8.0, 66.0, 1.0, 3.0, 5.0, 5.0, 9.0, 9.0, 11.0, 10.0,
89.0)
IDIAG = (1, 3, 6, 8, 13, 17, 22, 25, 34, 35)
IPARM = (1, 110, 0, 1, 1, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
* *
| 5.00 10.00 15.00 20.00 |
| 15.00 30.00 45.00 60.00 |
| 34.00 68.00 102.00 136.00 |
| 40.00 80.00 120.00 160.00 |
BX = | 66.00 132.00 198.00 264.00 |
| 78.00 156.00 234.00 312.00 |
| 96.00 192.00 288.00 384.00 |
| 90.00 180.00 270.00 360.00 |
| 142.00 284.00 426.00 568.00 |
| . . . . |
* *
A = (1.0, 1.0, .5, 1.0, 1.0, .333, 1.0, .25, 1.0, 1.0, 1.0,
1.0, .2, 1.0, 1.0, 1.0, .167, 1.0, 1.0, 1.0, 1.0, .143,
1.0, 1.0, .125, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
.111)
IDIAG =(same as input)
IPARM = (1, 110, 0, 1, 1, . , . , . , . , 0, . , . , . , . , . ,
9, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 9.89, 1.32, 11.0, . , . , . , . , . , . , . )
* *
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
BX = | 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| 1.00 2.00 3.00 4.00 |
| . . . . |
* *
This subroutine solves a general or symmetric sparse linear system of equations, using an iterative algorithm, with or without preconditioning. The methods include conjugate gradient (CG), conjugate gradient squared (CGS), generalized minimum residual (GMRES), more smoothly converging variant of the CGS method (Bi-CGSTAB), or transpose-free quasi-minimal residual method (TFQMR). The preconditioners include an incomplete LU factorization, an incomplete Cholesky factorization (for positive definite symmetric matrices), diagonal scaling, or symmetric successive over-relaxation (SSOR) with two possible choices for the diagonal matrix: one uses the absolute values sum of the input matrix, and the other uses the diagonal obtained from the LU factorization. The sparse matrix is stored using storage-by-rows for general matrices and upper- or lower-storage-by-rows for symmetric matrices. Matrix A and vectors x and b are used:
where A, x, and b contain long-precision real numbers.
| Fortran | CALL DSRIS (stor, init, n, ar, ja, ia, b, x, iparm, rparm, aux1, naux1, aux2, naux2) |
| C and C++ | dsris (stor, init, n, ar, ja, ia, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
| PL/I | CALL DSRIS (stor, init, n, ar, ja, ia, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
If stor = 'G', A is a general sparse matrix, stored using storage-by-rows.
If stor = 'U', A is a symmetric sparse matrix, stored using upper-storage-by-rows.
If stor = 'L', A is a symmetric sparse matrix, stored using lower-storage-by-rows.
Specified as: a single character. It must be 'G', 'U', or 'L'.
If init = 'I', the preconditioning matrix is computed, the internal representation of the sparse matrix is generated, and the iteration procedure is performed. The coefficient matrix and preconditioner in internal format are saved in aux1.
If init = 'S', the iteration procedure is performed using the coefficient matrix and the preconditioner in internal format, stored in aux1, created in a preceding call to this subroutine with init = 'I'. You use this option to solve the same matrix for different right-hand sides, b, optimizing your performance. As long as you do not change the coefficient matrix and preconditioner in aux1, any number of calls can be made with init = 'S'.
Specified as: a single character. It must be 'I' or 'S'.
If IPARM(1) > 0, IPARM(1) is the maximum number of iterations allowed.
If IPARM(1) = 0, the following default values are used:
If IPARM(2) = 1, the conjugate gradient (CG) method is used. Note that this algorithm should only be used with positive definite symmetric matrices.
If IPARM(2) = 2, the conjugate gradient squared (CGS) method is used.
If IPARM(2) = 3, the generalized minimum residual (GMRES) method, restarted after k steps, is used.
If IPARM(2) = 4, the more smoothly converging variant of the CGS method (Bi-CGSTAB) is used.
If IPARM(2) = 5, the transpose-free quasi-minimal residual method (TFQMR) is used.
If IPARM(2) <> 3, then IPARM(3) is not used.
If IPARM(2) = 3, then IPARM(3) = k, where k is the number of steps after which the generalized minimum residual method is restarted. A value for k in the range of 5 to 10 is suitable for most problems.
If IPARM(4) = 1, the system is not preconditioned.
If IPARM(4) = 2, the system is preconditioned by a diagonal matrix.
If IPARM(4) = 3, the system is preconditioned by SSOR splitting with the diagonal given by the absolute values sum of the input matrix.
If IPARM(4) = 4, the system is preconditioned by an incomplete LU factorization.
If IPARM(4) = 5, the system is preconditioned by SSOR splitting with the diagonal given by the incomplete LU factorization.
| Note: | The multithreaded version of DSRIS only runs on multiple threads when IPARM(4) = 1 or 2. |
If IPARM(5) = 1, the iterative method is stopped when:
| Note: | IPARM(5) = 1 is the default value assumed by ESSL if you do not specify one of the values described here; therefore, if you do not update your program to set an IPARM(5) value, you, by default, use the above stopping criterion. |
If IPARM(5) = 2, the iterative method is stopped when:
If IPARM(5) = 3, the iterative method is stopped when:
| Note: | Stopping criterion 3 performs poorly with the TFQMR method; therefore, if you specify TFQMR (IPARM(2) = 5), you should not specify stopping criterion 3. |
Specified as: an array of (at least) length 6, containing fullword integers, where:
RPARM(1) is the relative accuracy epsilon used in the stopping criterion. See "Notes".
RPARM(2), see 'On Return'.
RPARM(3) has the following meaning, where:
Specified as: a one-dimensional array of (at least) length 3, containing long-precision real numbers, where:
If init = 'I', the working storage is computed. It can contain any values.
If init = 'S', the working storage is used in solving the linear system. It contains the coefficient matrix and preconditioner in internal format, computed in an earlier call to this subroutine.
Specified as: an area of storage, containing naux1 long-precision real numbers.
Specified as: a fullword integer, where:
In these formulas nw has the following value:
| Note: | If you receive an attention message, you have not specified sufficient auxiliary storage to achieve optimal performance, but it is enough to perform the computation. To obtain optimal performance, you need to use the amount given by the attention message. |
If naux2 = 0 and error 2015 is unrecoverable, aux2 is ignored.
Otherwise, it is working storage used by this subroutine that is available for use by the calling program between calls to this subroutine.
Specified as: an area of storage, containing naux2 long-precision real numbers.
If naux2 = 0 and error 2015 is unrecoverable, DSRIS dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise,
Returned as: a one-dimensional array, containing long-precision real numbers. The number of elements in this array can be determined by subtracting 1 from the value in IA(n+1).
Returned as: a one-dimensional array, containing fullword integers; 1 <= (JA elements) <= n. The number of elements in this array can be determined by subtracting 1 from the value in IA(n+1).
IPARM(1) through IPARM(5) are unchanged.
IPARM(6) contains the number of iterations performed by this subroutine.
Returned as: a one-dimensional array of length 6, containing fullword integers.
RPARM(1) is unchanged.
RPARM(2) contains the estimate of the error of the solution. If the process converged, RPARM(2) <= epsilon.
RPARM(3) is unchanged.
Returned as: a one-dimensional array of length 3, containing long-precision real numbers.
In some cases, you can specify a different algorithm in IPARM(2) when making calls with init = 'S'. (See "Example 2".) However, DSRIS sometimes needs different information in aux1 for different algorithms. When this occurs, DSRIS issues an attention message, continues processing the computation, and then resets the contents of aux1. Your performance is not improved in this case, which is functionally equivalent to calling DSRIS with init = 'I'.
For the stopping criteria specified in IPARM(5), the relative accuracy epsilon (in RPARM(1)) must be specified reasonably (10-4 to 10-8). If you specify a larger epsilon, the algorithm takes fewer iterations to converge to a solution. If you specify a smaller epsilon, the algorithm requires more iterations and computer time, but converges to a more precise solution. If the value you specify is unreasonably small, the algorithm may fail to converge within the number of iterations it is allowed to perform.
The linear system:
is solved using one of the following methods: conjugate gradient (CG), conjugate gradient squared (CGS), generalized minimum residual (GMRES), more smoothly converging variant of the CGS method (Bi-CGSTAB), or transpose-free quasi-minimal residual method (TFQMR), where:
One of the following preconditioners is used:
See references [36], [53], [76], [80], [83], and [89].
When you call this subroutine to solve a system for the first time, you specify init = 'I'. After that, you can solve the same system any number of times by calling this subroutine each time with init = 'S'. These subsequent calls use the coefficient matrix and preconditioner, stored in internal format in aux1. You optimize performance by doing this, because certain portions of the computation have already been performed.
Error 2015 is unrecoverable, naux2 = 0, and unable to allocate work area.
The following errors, with their corresponding return codes, can occur in this subroutine. For details on error handling, see "What Can You Do about ESSL Computational Errors?".
This example finds the solution of the linear system Ax = b for the sparse matrix A, which is stored by rows in arrays AR, IA, and JA. The system is solved using the Bi-CGSTAB algorithm. The iteration is stopped when the norm of the residual is less than the given threshold specified in RPARM(1). The algorithm is allowed to perform 20 iterations. The process converges after 9 iterations. Matrix A is:
* *
| 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 0.0 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 |
* *
STOR INIT N AR JA IA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSRIS( 'G' , 'I' , 9 , AR , JA , IA , B , X , IPARM , RPARM , AUX1 , 98 , AUX2 , 63 )
AR = (2.0, 2.0, -1.0, 1.0, 2.0, 1.0, 2.0, -1.0, 1.0, 2.0, -1.0,
1.0, 2.0, -1.0, 1.0, 2.0, -1.0, 1.0, 2.0, -1.0, 1.0, 2.0)
JA = (1, 2, 3, 2, 3, 1, 4, 5, 4, 5, 6, 5, 6, 7, 6, 7, 8, 7, 8,
9, 8, 9)
IA = (1, 2, 4, 6, 9, 12, 15, 18, 21, 23)
B = (2.0, 1.0, 3.0, 2.0, 2.0, 2.0, 2.0, 2.0, 3.0)
X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
IPARM(1) = 20
IPARM(2) = 4
IPARM(3) = 0
IPARM(4) = 1
IPARM(5) = 10
RPARM(1) = 1.D-7
RPARM(3) = 1.0
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(6) = 9 RPARM(2) = 0.29D-16
This example finds the solution of the linear system Ax = b for the same sparse matrix A used in Example 1. It also uses the same right-hand side in b and the same initial guesses in x. However, the system is solved using a different algorithm, conjugate gradient squared (CGS). Because INIT is 'S', the best performance is achieved. The iteration is stopped when the norm of the residual is less than the given threshold specified in RPARM(1). The algorithm is allowed to perform 20 iterations. The process converges after 9 iterations.
STOR INIT N AR JA IA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSRIS( 'G' , 'S' , 9 , AR , JA , IA , B , X , IPARM , RPARM , AUX1 , 98 , AUX2 , 63 )
AR =(same as input AR in Example 1) JA =(same as input JA in Example 1) IA =(same as input IA in Example 1) B =(same as input B in Example 1) X =(same as input X in Example 1) IPARM(1) = 20 IPARM(2) = 2 IPARM(3) = 0 IPARM(4) = 1 IPARM(5) = 10 RPARM(1) = 1.D-7 RPARM(3) = 1.0
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(6) = 9 RPARM(2) = 0.42D-19
This example finds the solution of the linear system Ax = b for the sparse matrix A, which is stored by rows in arrays AR, IA, and JA. The system is solved using the two-term conjugate gradient method (CG), preconditioned by incomplete LU factorization. The iteration is stopped when the norm of the residual is less than the given threshold specified in RPARM(1). The algorithm is allowed to perform 20 iterations. The process converges after 1 iteration. Matrix A is:
* *
| 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 |
* *
STOR INIT N AR JA IA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSRIS( 'G' , 'I' , 9 , AR , JA , IA , B , X , IPARM , RPARM , AUX1 , 223 , AUX2 , 36 )
AR = (2.0, -1.0, 2.0, -1.0, -1.0, 2.0, -1.0, -1.0, 2.0, -1.0,
-1.0, 2.0, -1.0, -1.0, 2.0, -1.0, -1.0, 2.0, -1.0, -1.0,
2.0, -1.0, 2.0)
JA = (1, 3, 2, 4, 1, 3, 5, 2, 4, 6, 3, 5, 7, 4, 6, 8, 5, 7, 9,
6, 8, 7, 9)
IA = (1, 3, 5, 8, 11, 14, 17, 20, 22, 24)
B = (1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0)
X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
IPARM(1) = 20
IPARM(2) = 1
IPARM(3) = 0
IPARM(4) = 4
IPARM(5) = 1
RPARM(1) = 1.D-7
RPARM(3) = 1.0
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(6) = 1 RPARM(2) = 0.16D-15
This example finds the solution of the linear system Ax = b for the same sparse matrix A used in Example 3. However, matrix A is stored using upper-storage-by-rows in arrays AR, IA, and JA. The system is solved using the generalized minimum residual (GMRES), restarted after 5 steps and preconditioned with SSOR splitting. The iteration is stopped when the norm of the residual is less than the given threshold specified in RPARM(1). The algorithm is allowed to perform 20 iterations. The process converges after 12 iterations.
STOR INIT N AR JA IA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSRIS( 'U' , 'I' , 9 , AR , JA , IA , B , X , IPARM , RPARM , AUX1 , 219 , AUX2 , 109 )
AR = (2.0, -1.0, 2.0, -1.0, 2.0, -1.0, 2.0, -1.0, 2.0, -1.0,
2.0, -1.0, 2.0, -1.0, 2.0, 2.0)
JA = (1, 3, 2, 4, 3, 5, 4, 6, 5, 7, 6, 8, 7, 9, 8, 9)
IA = (1, 3, 5, 7, 9, 11, 13, 15, 16, 17)
B = (1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0)
X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
IPARM(1) = 20
IPARM(2) = 3
IPARM(3) = 5
IPARM(4) = 3
IPARM(5) = 1
RPARM(1) = 1.D-7
RPARM(3) = 2.0
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(6) = 12 RPARM(2) = 0.33D-7
This subroutine solves a symmetric, positive definite or negative definite linear system, using the conjugate gradient method, with or without preconditioning by an incomplete Cholesky factorization, for a sparse matrix stored in compressed-matrix storage mode. Matrix A and vectors x and b are used:
where A, x, and b contain long-precision real numbers.
Notes:
| Fortran | CALL DSMCG (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2) |
| C and C++ | dsmcg (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
| PL/I | CALL DSMCG (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
If IPARM(1) > 0, IPARM(1) is the maximum number of iterations allowed.
If IPARM(1) = 0, the following default values are used:
If IPARM(2) = 0, the conjugate gradient iterative procedure is stopped when:
where r = b-Ax is the residual, and epsilon is the desired relative accuracy. epsilon is stored in RPARM(1).
If IPARM(2) = 1, the conjugate gradient iterative procedure is stopped when:
where lambda is an estimate to the minimum eigenvalue of the iteration matrix. lambda is computed adaptively by this program and, on output, is stored in RPARM(2).
If IPARM(2) = 2, the conjugate gradient iterative procedure is stopped when:
where lambda is a predetermined estimate to the minimum eigenvalue of the iteration matrix. This eigenvalue estimate, on input, is stored in RPARM(2) and may be obtained by an earlier call to this subroutine with the same matrix.
If IPARM(3) = 0, the system is not preconditioned.
If IPARM(3) = 10, the system is preconditioned by an incomplete Cholesky factorization.
If IPARM(3) = -10, the system is preconditioned by an incomplete Cholesky factorization, where the factorization matrix was computed in an earlier call to this subroutine and is stored in aux2.
RPARM(1) > 0, is the relative accuracy epsilon used in the stopping criterion.
RPARM(2) > 0, is the estimate of the smallest eigenvalue, lambda, of the iteration matrix. It is only used when IPARM(2) = 2.
RPARM(3), see 'On Return'.
Specified as: a one-dimensional array of (at least) length 3, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, aux1 is ignored.
Otherwise, it is a storage work area used by this subroutine, which is available for use by the calling program between calls to this subroutine. Its size is specified by naux1.
Specified as: an area of storage, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, DSMCG dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux1 must have at least the following value, where:
If IPARM(2) = 0 or 2, use naux1 >= 3m.
If IPARM(2) = 1 and IPARM(1) <> 0, use naux1 >= 3m+2(IPARM(1)).
If IPARM(2) = 1 and IPARM(1) = 0, use naux1 >= 3m+600.
IPARM(1) is unchanged.
IPARM(2) is unchanged.
IPARM(3) is unchanged.
IPARM(4) contains the number of iterations performed by this subroutine.
Returned as: a one-dimensional array of length 4, containing fullword integers.
RPARM(1) is unchanged.
RPARM(2) is unchanged if IPARM(2) = 0 or 2. If IPARM(2) = 1, RPARM(2) contains lambda, an estimate of the smallest eigenvalue of the iteration matrix.
RPARM(3) contains the estimate of the error of the solution. If the process converged, RPARM(3) <= epsilon.
Returned as: a one-dimensional array of length 3, containing long-precision real numbers; lambda > 0.
If IPARM(3) = 10, aux2 contains the incomplete Cholesky factorization of matrix A.
If IPARM(3) = -10, aux2 is unchanged.
See "Notes" for additional information on aux2. Returned as: an area of storage, containing long-precision real numbers.
where lambda is an estimate of the minimum eigenvalue of the iteration matrix, which is either estimated adaptively or given by the user. As a result, if you specify a larger epsilon, the algorithm takes fewer iterations to converge to a solution. If you specify a smaller epsilon, the algorithm requires more iterations and computer time, but converges to a more precise solution. If the value you specify is unreasonably small, the algorithm may fail to converge within the number of iterations it is allowed to perform.
The sparse positive definite or negative definite linear system:
is solved, where:
The system is solved using the two-term conjugate gradient method, with or without preconditioning by an incomplete Cholesky factorization. In both cases, the matrix is scaled by the square root of the diagonal.
See references [59] and [62]. [36].
If your program uses a sparse matrix stored by rows and you want to use this subroutine, first convert your sparse matrix to compressed-matrix storage mode by using the subroutine DSRSM described on page DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode.
Error 2015 is unrecoverable, naux1 = 0, and unable to allocate work area.
The following errors, with their corresponding return codes, can occur in this subroutine. Where a value of i is indicated, it can be determined at run time by use of the ESSL error-handling facilities. To obtain this information, you must use ERRSET to change the number of allowable errors for that particular error code in the ESSL error option table; otherwise, the default value causes your program to terminate when the error occurs. For details, see "What Can You Do about ESSL Computational Errors?".
This example finds the solution of the linear system Ax = b for the sparse matrix A, which is stored in compressed-matrix storage mode in arrays AC and KA. The system is solved using the conjugate gradient method. Matrix A is:
* *
| 2.0 0.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 -1.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| -1.0 0.0 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 -1.0 2.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 -1.0 2.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 -1.0 2.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 -1.0 2.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -1.0 2.0 |
* *
| Note: | For input matrix KA, ( . ) indicates any value between 1 and 9. |
M NZ AC KA LDA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
CALL DSMCG( 9 , 3 , AC, KA, 9 , B , X, IPARM, RPARM, AUX1, 27 , AUX2, 0 )
IPARM(1) = 20 IPARM(2) = 0 IPARM(3) = 0 RPARM(1) = 1.D-7
* *
| 2.0 -1.0 0.0 |
| 2.0 -1.0 0.0 |
| -1.0 2.0 0.0 |
| -1.0 2.0 -1.0 |
AC = | -1.0 2.0 -1.0 |
| -1.0 2.0 -1.0 |
| -1.0 2.0 -1.0 |
| -1.0 2.0 -1.0 |
| -1.0 2.0 0.0 |
* *
* *
| 1 4 . |
| 2 3 . |
| 2 3 . |
| 1 4 5 |
KA = | 4 5 6 |
| 5 6 7 |
| 6 7 8 |
| 7 8 9 |
| 8 9 . |
* *
B = (1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 5 RPARM(2) = 0 RPARM(3) = 0.351D-15
This example finds the solution of the linear system Ax = b for the same sparse matrix A as in Example 1, which is stored in compressed-matrix storage mode in arrays AC and KA. The system is solved using the conjugate gradient method, preconditioned with an incomplete Cholesky factorization. The smallest eigenvalue of the iteration matrix is computed and used in stopping the computation.
| Note: | For input matrix KA, ( . ) indicates any value between 1 and 9. |
M NZ AC KA LDA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
CALL DSMCG( 9 , 3 , AC, KA, 9 , B , X, IPARM, RPARM, AUX1, 67 , AUX2, 74 )
IPARM(1) = 20 IPARM(2) = 1 IPARM(3) = 10 RPARM(1) = 1.D-7 AC =(same as input AC in Example 1) KA =(same as input KA in Example 1) B = (1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 1 RPARM(2) = 1 RPARM(3) = 0.100D-15
This subroutine solves a symmetric, positive definite or negative definite linear system, using the two-term conjugate gradient method, with or without preconditioning by an incomplete Cholesky factorization, for a sparse matrix stored in compressed-diagonal storage mode. Matrix A and vectors x and b are used:
where A, x, and b contain long-precision real numbers.
| Fortran | CALL DSDCG (iopt, m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2) |
| C and C++ | dsdcg (iopt, m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
| PL/I | CALL DSDCG (iopt, m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
If iopt = 0, all the nonzero diagonals of the sparse matrix are stored in compressed-diagonal storage mode.
If iopt = 1, the sparse matrix, stored in compressed-diagonal storage mode, is symmetric. Only the main diagonal and one of each pair of identical diagonals are stored in array AD.
Specified as: a fullword integer; iopt = 0 or 1.
If m > 0, then nd > 0.
If m = 0, then nd >= 0.
Specified as: an lda by (at least) nd array, containing long-precision real numbers.
Specified as: a one-dimensional array of (at least) length nd, containing fullword integers, where 1-m <= (elements of LA) <= m-1.
If IPARM(1) > 0, IPARM(1) is the maximum number of iterations allowed.
If IPARM(1) = 0, the following default values are used:
If IPARM(2) = 0, the conjugate gradient iterative procedure is stopped when:
where r = b-Ax is the residual and epsilon is the desired relative accuracy. epsilon is stored in RPARM(1).
If IPARM(2) = 1, the conjugate gradient iterative procedure is stopped when:
where lambda is an estimate to the minimum eigenvalue of the iteration matrix. lambda is computed adaptively by this program and, on output, is stored in RPARM(2).
If IPARM(2) = 2, the conjugate gradient iterative procedure is stopped when:
where lambda is a predetermined estimate to the minimum eigenvalue of the iteration matrix. This eigenvalue estimate, on input, is stored in RPARM(2) and may be obtained by an earlier call to this subroutine with the same matrix.
If IPARM(3) = 0, the system is not preconditioned.
If IPARM(3) = 10, the system is preconditioned by an incomplete Cholesky factorization.
If IPARM(3) = -10, the system is preconditioned by an incomplete Cholesky factorization, where the factorization matrix was computed in an earlier call to this subroutine and is stored in aux2.
Specified as: an array of (at least) length 4, containing fullword integers, where:
RPARM(1) > 0, is the relative accuracy epsilon used in the stopping criterion.
RPARM(2) > 0, is the estimate of the smallest eigenvalue, lambda, of the iteration matrix. It is only used when IPARM(2) = 2.
RPARM(3), see 'On Return'.
Specified as: a one-dimensional array of (at least) length 3, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, aux1 is ignored.
Otherwise, it is a storage work area used by this subroutine, which is available for use by the calling program between calls to this subroutine. Its size is specified by naux1.
Specified as: an area of storage, containing long-precision real numbers.
Specified as: a fullword integer, where:
If naux = 0 and error 2015 is unrecoverable, DSDCG dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, it must have at least the following value, where:
If IPARM(2) = 0 or 2, use naux1 >= 3m.
If IPARM(2) = 1 and IPARM(1) <> 0, use naux1 >= 3m+2(IPARM(1)).
If IPARM(2) = 1 and IPARM(1) = 0, use naux1 >= 3m+600.
If iopt = 0, use naux2 >= m(1.5nd+2)1.5+2(m+6).
If iopt = 1, use naux2 >= m(3nd+2)+8.
IPARM(1) is unchanged.
IPARM(2) is unchanged.
IPARM(3) is unchanged.
IPARM(4) contains the number of iterations performed by this subroutine.
Returned as: a one-dimensional array of length 4, containing fullword integers.
RPARM(1) is unchanged.
RPARM(2) is unchanged if IPARM(2) = 0 or 2. If IPARM(2) = 1, RPARM(2) contains lambda, an estimate of the smallest eigenvalue of the iteration matrix.
RPARM(3) contains the estimate of the error of the solution. If the process converged, RPARM(3) <= epsilon.
Returned as: a one-dimensional array of length 3, containing long-precision real numbers; lambda > 0.
If IPARM(3) = 10, aux2 contains the incomplete Cholesky factorization of matrix A.
If IPARM(3) = -10, aux2 is unchanged.
See "Notes" for additional information on aux2. Returned as: an area of storage, containing long-precision real numbers.
where lambda is an estimate of the minimum eigenvalue of the iteration matrix, which is either estimated adaptively or given by the user. As a result, if you specify a larger epsilon, the algorithm takes fewer iterations to converge to a solution. If you specify a smaller epsilon, the algorithm requires more iterations and computer time, but converges to a more precise solution. If the value you specify is unreasonably small, the algorithm may fail to converge within the number of iterations it is allowed to perform.
The sparse positive definite or negative definite linear system:
is solved, where:
The system is solved using the two-term conjugate gradient method, with or without preconditioning by an incomplete Cholesky factorization. In both cases, the matrix is scaled by the square root of the diagonal.
See references [59] and [62]. [36].
Error 2015 is unrecoverable, naux1 = 0, and unable to allocate work area.
The following errors, with their corresponding return codes, can occur in this subroutine. Where a value of i is indicated, it can be determined at run time by use of the ESSL error-handling facilities. To obtain this information, you must use ERRSET to change the number of allowable errors for that particular error code in the ESSL error option table; otherwise, the default value causes your program to terminate when the error occurs. For details, see "What Can You Do about ESSL Computational Errors?".
This example finds the solution of the linear system Ax = b for sparse matrix A, which is stored in compressed-diagonal storage mode in arrays AD and LA. The system is solved using the two-term conjugate gradient method. In this example, IOPT = 0.. Matrix A is:
* *
| 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 -1.0 0.0 2.0 |
* *
IOPT M ND AD LDA LA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSDCG( 0 , 9 , 3 , AD , 9 , LA , B , X , IPARM , RPARM , AUX1 , 283 , AUX2 , 0 )
IPARM(1) = 20 IPARM(2) = 0 IPARM(3) = 0 RPARM(1) = 1.D-7
* *
| 2.0 0.0 -1.0 |
| 2.0 0.0 -1.0 |
| 2.0 -1.0 -1.0 |
| 2.0 -1.0 -1.0 |
AD = | 2.0 -1.0 -1.0 |
| 2.0 -1.0 -1.0 |
| 2.0 -1.0 -1.0 |
| 2.0 -1.0 0.0 |
| 2.0 -1.0 0.0 |
* *
LA = (0, -2, 2) B = (1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 5 RPARM(2) = 0 RPARM(3) = 0.46D-16
This example finds the solution of the linear system Ax = b for the same sparse matrix A as in Example 1, which is stored in compressed-diagonal storage mode in arrays AD and LA. The system is solved using the two-term conjugate gradient method. In this example, IOPT = 1, indicating that the matrix is symmetric, and only the main diagonal and one of each pair of identical diagonals are stored in array AD.
IOPT M ND AD LDA LA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL DSDCG( 1 , 9 , 2 , AD , 9 , LA , B , X , IPARM , RPARM , AUX1 , 283 , AUX2 , 80 )
IPARM(1) = 20 IPARM(2) = 0 IPARM(3) = 10 RPARM(1) = 1.D-7
* *
| 2.0 0.0 |
| 2.0 0.0 |
| 2.0 -1.0 |
| 2.0 -1.0 |
AD = | 2.0 -1.0 |
| 2.0 -1.0 |
| 2.0 -1.0 |
| 2.0 -1.0 |
| 2.0 -1.0 |
* *
LA = (0, -2) B = (1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 1 RPARM(2) = 0 RPARM(3) = 0.89D-16
This subroutine solves a general sparse linear system of equations using an iterative algorithm, conjugate gradient squared or generalized minimum residual, with or without preconditioning by an incomplete LU factorization. The subroutine is suitable for positive real matrices--that is, when the symmetric part of the matrix, (A+AT)/2, is positive definite. The sparse matrix is stored in compressed-matrix storage mode. Matrix A and vectors x and b are used:
where A, x, and b contain long-precision real numbers.
Notes:
| Fortran | CALL DSMGCG (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2) |
| C and C++ | dsmgcg (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
| PL/I | CALL DSMGCG (m, nz, ac, ka, lda, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
If IPARM(1) > 0, IPARM(1) is the maximum number of iterations allowed.
If IPARM(1) = 0, the following default values are used:
If IPARM(2) = 0, the conjugate gradient squared method is used.
If IPARM(2) = k, the generalized minimum residual method, restarted after k steps, is used. Note that the size of the work area aux1 becomes larger as k increases. A value for k in the range of 5 to 10 is suitable for most problems.
If IPARM(3) = 0, the system is not preconditioned.
If IPARM(3) = 10, the system is preconditioned by an incomplete LU factorization.
If IPARM(3) = -10, the system is preconditioned by an incomplete LU factorization, where the factorization matrix was computed in an earlier call to this subroutine and is stored in aux2.
RPARM(1) > 0, is the relative accuracy epsilon used in the stopping criterion. The iterative procedure is stopped when:
RPARM(2) is reserved.
RPARM(3), see 'On Return'.
Specified as: a one-dimensional array of (at least) length 3, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, aux1 is ignored.
Otherwise, it is a storage work area used by this subroutine, which is available for use by the calling program between calls to this subroutine. Its size is specified by naux1.
Specified as: an area of storage, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, DSMGCG dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, it must have at least the following value, where:
If IPARM(2) = 0, use naux1 >= 7m.
If IPARM(2) > 0, use naux1 >= (k+2)m+k(k+4)+1, where k = IPARM(2).
Specified as: an area of storage, containing long-precision real numbers.
IPARM(1) is unchanged.
IPARM(2) is unchanged.
IPARM(3) is unchanged.
IPARM(4) contains the number of iterations performed by this subroutine.
Returned as: a one-dimensional array of length 4, containing fullword integers.
RPARM(1) is unchanged.
RPARM(2) is reserved.
RPARM(3) contains the estimate of the error of the solution. If the process converged, RPARM(3) <= RPARM(1)
Returned as: a one-dimensional array of length 3, containing long-precision real numbers.
If IPARM(3) = 10, aux2 contains the incomplete LU factorization of matrix A.
If IPARM(3) = -10, aux2 is unchanged.
See "Notes" for additional information on aux2. Returned as: an area of storage, containing long-precision real numbers.
As a result, if you specify a larger epsilon, the algorithm takes fewer iterations to converge to a solution. If you specify a smaller epsilon, the algorithm requires more iterations and computer time, but converges to a more precise solution. If the value you specify is unreasonably small, the algorithm may fail to converge within the number of iterations it is allowed to perform.
The linear system:
is solved using either the conjugate gradient squared method or the generalized minimum residual method, with or without preconditioning by an incomplete LU factorization, where:
See references [80] and [82]. [36].
If your program uses a sparse matrix stored by rows and you want to use this subroutine, first convert your sparse matrix to compressed-matrix storage mode by using the subroutine DSRSM described on page DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode.
Error 2015 is unrecoverable, naux1 = 0, and unable to allocate work area.
The following errors, with their corresponding return codes, can occur in this subroutine. For details on error handling, see "What Can You Do about ESSL Computational Errors?".
This example finds the solution of the linear system Ax = b for the sparse matrix A, which is stored in compressed-matrix storage mode in arrays AC and KA. The system is solved using the conjugate gradient squared method. Matrix A is:
* *
| 2.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 2.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 0.0 0.0 2.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 0.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 -1.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 |
* *
| Note: | For input matrix KA, ( . ) indicates any value between 1 and 9. |
M NZ AC KA LDA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
CALL DSMGCG( 9 , 3 , AC , KA , 9 , B , X , IPARM , RPARM , AUX1 , 63 , AUX2 , 0 )
IPARM(1) = 20 IPARM(2) = 0 IPARM(3) = 0 RPARM(1) = 1.D-7
* *
| 2.0 0.0 0.0 |
| 2.0 -1.0 0.0 |
| 1.0 2.0 0.0 |
| 1.0 2.0 -1.0 |
AC = | 1.0 2.0 -1.0 |
| 1.0 2.0 -1.0 |
| 1.0 2.0 -1.0 |
| 1.0 2.0 -1.0 |
| 1.0 2.0 0.0 |
* *
* *
| 1 . . |
| 2 3 . |
| 2 3 . |
| 1 4 5 |
KA = | 4 5 6 |
| 5 6 7 |
| 6 7 8 |
| 7 8 9 |
| 8 9 . |
* *
B = (2.0, 1.0, 3.0, 2.0, 2.0, 2.0, 2.0, 2.0, 3.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 9 RPARM(3) = 0.150D-19
This example finds the solution of the linear system Ax = b for the same sparse matrix A as in Example 1, which is stored in compressed-matrix storage mode in arrays AC and KA. The system is solved using the generalized minimum residual method, restarted after 5 steps and preconditioned with an incomplete LU factorization. Most of the input is the same as in Example 1.
| Note: | For input matrix KA, ( . ) indicates any value between 1 and 9. |
M NZ AC KA LDA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
CALL DSMGCG( 9 , 3 , AC , KA , 9 , B , X , IPARM , RPARM , AUX1 , 109 , AUX2 , 46 )
IPARM(1) = 20 IPARM(2) = 5 IPARM(3) = 10 RPARM(1) = 1.D-7 AC =(same as input AC in Example 1) KA =(same as input KA in Example 1) B = (2.0, 1.0, 3.0, 2.0, 2.0, 2.0, 2.0, 2.0, 3.0) X = (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 2 RPARM(3) = 0.290D-15
This subroutine solves a general sparse linear system of equations using an iterative algorithm, conjugate gradient squared or generalized minimum residual, with or without preconditioning by an incomplete LU factorization. The subroutine is suitable for positive real matrices--that is, when the symmetric part of the matrix, (A+AT)/2, is positive definite. The sparse matrix is stored in compressed-diagonal storage mode. Matrix A and vectors x and b are used:
where A, x, and b contain long-precision real numbers.
| Fortran | CALL DSDGCG (m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2) |
| C and C++ | dsdgcg (m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
| PL/I | CALL DSDGCG (m, nd, ad, lda, la, b, x, iparm, rparm, aux1, naux1, aux2, naux2); |
If m > 0, then nd > 0.
If m = 0, then nd >= 0.
Specified as: a one-dimensional array of (at least) length nd, containing fullword integers, where 1-m <= (elements of LA) <= (m-1).
If IPARM(1) > 0, IPARM(1) is the maximum number of iterations allowed.
If IPARM(1) = 0, the following default values are used:
If IPARM(2) = 0, the conjugate gradient squared method is used.
If IPARM(2) = k, the generalized minimum residual method, restarted after k steps, is used. Note that the size of the work area aux1 becomes larger as k increases. A value for k in the range of 5 to 10 is suitable for most problems.
If IPARM(3) = 0, the system is not preconditioned.
If IPARM(3) = 10, the system is preconditioned by an incomplete LU factorization.
If IPARM(3) = -10, the system is preconditioned by an incomplete LU factorization, where the factorization matrix was computed in an earlier call to this subroutine and is stored in aux2.
If RPARM(1) > 0, is the relative accuracy epsilon used in the stopping criterion. The iterative procedure is stopped when:
RPARM(2) is reserved.
RPARM(3), see 'On Return'.
Specified as: a one-dimensional array of (at least) length 3, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, aux1 is ignored.
Otherwise, it is a storage work area used by this subroutine, which is available for use by the calling program between calls to this subroutine. Its size is specified by naux1.
Specified as: an area of storage, containing long-precision real numbers.
If naux1 = 0 and error 2015 is unrecoverable, DSDGCG dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux1 > 0 and must have at least the following value, where:
If IPARM(2) = 0, use naux1 >= 7m.
If IPARM(2) > 0, use naux1 >= (k+2)m+k(k+4)+1, where k = PARM(2).
Specified as: an area of storage, containing long-precision real numbers.
IPARM(1) is unchanged.
IPARM(2) is unchanged.
IPARM(3) is unchanged.
IPARM(4) contains the number of iterations performed by this subroutine.
Returned as: a one-dimensional array of length 4, containing fullword integers.
RPARM(1) is unchanged.
RPARM(2) is reserved.
RPARM(3) contains the estimate of the error of the solution. If the process converged, RPARM(3) <= RPARM(1).
Returned as: a one-dimensional array of length 3, containing long-precision real numbers.
If IPARM(3) = 10, aux2 contains the incomplete LU factorization of matrix A.
If IPARM(3) = -10, aux2 is unchanged.
See "Notes" for additional information on aux2. Returned as: an area of storage, containing long-precision real numbers.
As a result, if you specify a larger epsilon, the algorithm takes fewer iterations to converge to a solution. If you specify a smaller epsilon, the algorithm requires more iterations and computer time, but converges to a more precise solution. If the value you specify is unreasonably small, the algorithm may fail to converge within the number of iterations it is allowed to perform.
The linear system:
is solved using either the conjugate gradient squared method or the generalized minimum residual method, with or without preconditioning by an incomplete LU factorization, where:
See references [80] and [82]. [36].
Error 2015 is unrecoverable, naux1 = 0, and unable to allocate work area.
The following errors, with their corresponding return codes, can occur in this subroutine. For details on error handling, see "What Can You Do about ESSL Computational Errors?".
This example finds the solution of the linear system Ax = b for the sparse matrix A, which is stored in compressed-diagonal storage mode in arrays AD and LA. The system is solved using the conjugate gradient squared method. Matrix A is:
* *
| 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 0.0 |
| 0.0 0.0 0.0 2.0 0.0 -1.0 0.0 0.0 0.0 |
| 1.0 0.0 0.0 0.0 2.0 0.0 -1.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 2.0 0.0 -1.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 0.0 2.0 0.0 -1.0 |
| 0.0 0.0 0.0 1.0 0.0 0.0 0.0 2.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 2.0 |
* *
M ND AD LDA LA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
DSDGCG( 9 , 3 , AD , 9 , LA , B , X , IPARM , RPARM , AUX1 , 63 , AUX2 , 0 )
IPARM(1) = 20 IPARM(2) = 0 IPARM(3) = 0 RPARM(1) = 1.D-7
* *
| 2.0 -1.0 0.0 |
| 2.0 -1.0 0.0 |
| 2.0 -1.0 0.0 |
| 2.0 -1.0 0.0 |
AD = | 2.0 -1.0 1.0 |
| 2.0 -1.0 1.0 |
| 2.0 -1.0 1.0 |
| 2.0 0.0 1.0 |
| 2.0 0.0 1.0 |
* *
LA = (0, 2, -4) B = (1, 1, 1, 1, 2, 2, 2, 3, 3) X = (0, 0, 0, 0, 0, 0, 0, 0, 0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 8 RPARM(3) = 0.308D-17
This example finds the solution of the linear system Ax = b for the same sparse matrix A as in Example 1, which is stored in compressed-diagonal storage mode in arrays AD and LA. The system is solved using the generalized minimum residual method, restarted after 5 steps and preconditioned with an incomplete LU factorization. Most of the input is the same as in Example 1.
M ND AD LDA LA B X IPARM RPARM AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | |
CALL DSDGCG( 9 , 3 , AD , 9 , LA , B , X , IPARM , RPARM , AUX1 , 109 , AUX2 , 46 )
IPARM(1) = 20 IPARM(2) = 5 IPARM(3) = 10 RPARM(1) = 1.D-7 AD =(same as input AD in Example 1) LA =(same as input LA in Example 1) B = (1, 1, 1, 1, 2, 2, 2, 3, 3) X = (0, 0, 0, 0, 0, 0, 0, 0, 0)
X = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) IPARM(4) = 6 RPARM(3) = 0.250D-15
This section contains the linear least squares subroutine descriptions.
These subroutines compute the singular value decomposition of general
matrix A in preparation for solving linear least squares problems.
To compute the minimal norm linear least squares solution of
AX is congruent to B, follow the call to these
subroutines with a call to SGESVS or DGESVS, respectively.
| A, B, s, aux | Subroutine |
| Short-precision real | SGESVF |
| Long-precision real | DGESVF |
| Fortran | CALL SGESVF | DGESVF (iopt, a, lda, b, ldb, nb, s, m, n, aux, naux) |
| C and C++ | sgesvf | dgesvf (iopt, a, lda, b, ldb, nb, s, m, n, aux, naux); |
| PL/I | CALL SGESVF | DGESVF (iopt, a, lda, b, ldb, nb, s, m, n, aux, naux); |
If iopt = 0 or 10, singular values are computed.
If iopt = 1 or 11, singular values and V are computed.
If iopt = 2 or 12, singular values, V, and UTB are computed.
Specified as: a fullword integer; iopt = 0, 1, 2, 10, 11, or 12.
If iopt < 10, singular values are unordered.
If iopt >= 10, singular values are sorted in descending order and, if applicable, the columns of V and the rows of UTB are swapped to correspond to the sorted singular values.
If iopt = 0, 1, 10, or 11, this argument is not used in the computation.
If iopt = 2 or 12, it is the m by nb matrix B.
Specified as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 114.
If this subroutine is followed by a call to SGESVS or DGESVS, B should contain the right-hand side of the linear least squares problem, AX is congruent to B. (The nb column vectors of B contain right-hand sides for nb distinct linear least squares problems.) However, if the matrix UT is desired on output, B should be equal to the identity matrix of order m.
If iopt = 0, 1, 10, or 11, this argument is not used in the computation.
If iopt = 2 or 12, it is the leading dimension of the array specified for b.
Specified as: a fullword integer. It must have the following values, where:
If iopt = 0, 1, 10, or 11, ldb > 0.
If iopt = 2 or 12, ldb > 0 and ldb >= max(m, n).
If iopt = 0, 1, 10, or 11, this argument is not used in the computation.
If iopt = 2 or 12, it is the number of columns in matrix B.
Specified as: a fullword integer; if iopt = 2 or 12, nb > 0.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing numbers of the data type indicated in Table 114.
If naux = 0 and error 2015 is unrecoverable, SGESVF and DGESVF dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, It must have the following value, where:
If iopt = 0 or 10, naux >= n+max(m, n).
If iopt = 1 or 11, naux >= 2n+max(m, n).
If iopt = 2 or 12, naux >= 2n+max(m, n, nb).
If iopt = 0, or 10, A is overwritten; that is, the original input is not preserved.
If iopt = 1, 2, 11, or 12, A contains the real orthogonal matrix V, of order n, in its first n rows and n columns. If iopt = 11 or 12, the columns of V are swapped to correspond to the sorted singular values. If m > n, rows n+1, n+2, ..., m of array A are overwritten; that is, the original input is not preserved.
Returned as: an lda by (at least) n array, containing numbers of the data type indicated in Table 114.
If iopt = 0, 1, 10, or 11, B is not used in the computation.
If iopt = 2 or 12, B is overwritten by the n by nb matrix UTB.
If iopt = 12, the rows of UTB are swapped to correspond to the sorted singular values. If m > n, rows n+1, n+2, ..., m of array B are overwritten; that is, the original input is not preserved.
Returned as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 114.
If iopt < 10, the singular values are unordered in s.
If iopt >= 10, the singular values are sorted in descending order in s; that is, s1 >= s2 >= ... >= sn >= 0. If applicable, the columns of V and the rows of UTB are swapped to correspond to the sorted singular values.
See "Example".
The singular value decomposition of a real general matrix is computed as follows:
where:
If m or n is equal to 0, no computation is performed.
One of the following algorithms is used:
If R = XWYT is the singular value decomposition of R, the singular value decomposition of matrix A is given by:
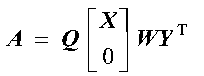
where:
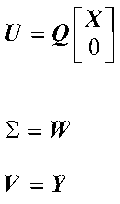
Also, see references [13], [55], [72], and pages 134 to 151 in reference [93]. These algorithms have a tendency to generate underflows that may hurt overall performance. The system default is to mask underflow, which improves the performance of these subroutines.
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
Singular value (i) failed to converge after (x) iterations.
This example shows how to find only the singular values, s, of a real long-precision general matrix A, where:
IOPT A LDA B LDB NB S M N AUX NAUX
| | | | | | | | | | |
CALL DGESVF( 0 , A , 4 , DUMMY , 1 , 0 , S , 4 , 3 , AUX , 7 )
* *
| 1.0 2.0 3.0 |
A = | 4.0 5.0 6.0 |
| 7.0 8.0 9.0 |
| 10.0 11.0 12.0 |
* *
S = (25.462, 1.291, 0.000)
This example computes the singular values, s, of a real long-precision general matrix A and the matrix V, where:
IOPT A LDA B LDB NB S M N AUX NAUX
| | | | | | | | | | |
CALL DGESVF( 1 , A , 3 , DUMMY , 1 , 0 , S , 3 , 3 , AUX , 9 )
* *
| 2.0 1.0 1.0 |
A = | 4.0 1.0 0.0 |
| -2.0 2.0 1.0 |
* *
* *
| -0.994 0.105 -0.041 |
A = | -0.112 -0.870 0.480 |
| -0.015 -0.482 -0.876 |
* *
S = (4.922, 2.724, 0.597)
This example computes the singular values, s, and computes matrices V and UTB in preparation for solving the underdetermined system AX is congruent to B, where:
IOPT A LDA B LDB NB S M N AUX NAUX
| | | | | | | | | | |
CALL DGESVF( 2 , A , 3 , B , 3 , 1 , S , 2 , 3 , AUX , 9 )
* *
| 1.0 2.0 2.0 |
A = | 2.0 4.0 5.0 |
| . . . |
* *
* *
| 1.0 |
B = | 4.0 |
| . |
* *
* *
| -0.304 -0.894 0.328 |
A = | -0.608 0.447 0.656 |
| -0.733 0.000 -0.680 |
* *
* *
| -4.061 |
B = | 0.000 |
| -0.714 |
* *
S = (7.342, 0.000, 0.305)
This example computes the singular values, s, and matrices V and UTB in preparation for solving the overdetermined system AX is congruent to B, where:
IOPT A LDA B LDB NB S M N AUX NAUX
| | | | | | | | | | |
CALL DGESVF( 2 , A , 3 , B , 3 , 2 , S , 3 , 2 , AUX , 7 )
* *
| 1.0 4.0 |
A = | 2.0 5.0 |
| 3.0 6.0 |
* *
* *
| 7.0 10.0 |
B = | 8.0 11.0 |
| 9.0 12.0 |
* *
* *
| 0.922 -0.386 |
A = | -0.386 -0.922 |
| . . |
* *
* *
| -1.310 -2.321 |
B = | -13.867 -18.963 |
| . . |
* *
X = (0.773, 9.508)
This example computes the singular values, s, and matrices V and UTB in preparation for solving the overdetermined system AX is congruent to B. The singular values are sorted in descending order, and the columns of V and the rows of UTB are swapped to correspond to the sorted singular values.
IOPT A LDA B LDB NB S M N AUX NAUX
| | | | | | | | | | |
CALL DGESVF( 12 , A , 3 , B , 3 , 2 , S , 3 , 2 , AUX , 7 )
* *
| 1.0 4.0 |
A = | 2.0 5.0 |
| 3.0 6.0 |
* *
* *
| 7.0 10.0 |
B = | 8.0 11.0 |
| 9.0 12.0 |
* *
* *
| -0.386 0.922 |
A = | -0.922 -0.386 |
| . . |
* *
* *
| -13.867 -18.963 |
B = | -1.310 -2.321 |
| . . |
* *
S = (9.508, 0.773)
These subroutines compute the minimal norm linear least squares solution of
AX is congruent to B, where A is a
general matrix, using the singular value decomposition computed by SGESVF or
DGESVF.
| V, UB, X, s, tau | Subroutine |
| Short-precision real | SGESVS |
| Long-precision real | DGESVS |
| Fortran | CALL SGESVS | DGESVS (v, ldv, ub, ldub, nb, s, x, ldx, m, n, tau) |
| C and C++ | sgesvs | dgesvs (v, ldv, ub, ldub, nb, s, x, ldx, m, n, tau); |
| PL/I | CALL SGESVS | DGESVS (v, ldv, ub, ldub, nb, s, x, ldx, m, n, tau); |
Specified as: an ldv by (at least) n array, containing numbers of the data type indicated in Table 115.
Specified as: an ldub by (at least) nb array, containing numbers of the data type indicated in Table 115.
Specified as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 115; si >= 0.
Returned as: an ldx by (at least) nb array, containing numbers of the data type indicated in Table 115.
where DELTAij are the errors in aij. In problems where the matrix elements are known exactly or are only affected by roundoff errors:
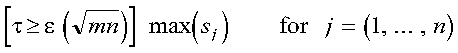
where:
For more information, see references [13], [55], [72], and pages 134 to 151 in reference [93].
The minimal norm linear least squares solution of AX is congruent to B, where A is a real general matrix, is computed using the singular value decomposition, produced by a preceding call to SGESVF or DGESVF. From SGESVF or DGESVF, the singular value decomposition of A is given by the following:
The linear least squares of solution X, for AX is congruent to B, is given by the following formula:
where:
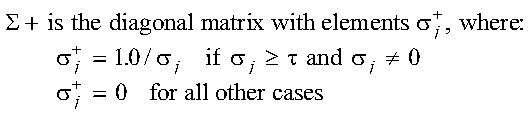
If m or n is equal to 0, no computation is performed. See references [13], [55], [72], and pages 134 to 151 in reference [93]. These algorithms have a tendency to generate underflows that may hurt overall performance. The system default is to mask underflow, which improves the performance of these subroutines.
None
This example finds the linear least squares solution for the underdetermined system AX is congruent to B, using the singular value decomposition computed by DGESVF. Matrix A is:
* *
| 1.0 2.0 2.0 |
| 2.0 4.0 5.0 |
* *
and matrix B is:
* *
| 1.0 |
| 4.0 |
* *
On output, matrix UTB is overwritten.
| Note: | This example corresponds to Example 3 of DGESVF on page "Example 3". |
V LDV UB LDUB NB S X LDX M N TAU
| | | | | | | | | | |
CALL DGESVS( V , 3 , UB , 3 , 1 , S , X , 3 , 2 , 3 , TAU )
* *
| -0.304 -0.894 0.328 |
V = | -0.608 0.447 0.656 |
| -0.733 0.000 -0.680 |
* *
* *
| -4.061 |
UB = | 0.000 |
| -0.714 |
* *
S = (7.342, 0.000, 0.305)
TAU = 0.3993D-14
* *
| -0.600 |
X = | -1.200 |
| 2.000 |
* *
This example finds the linear least squares solution for the overdetermined system AX is congruent to B, using the singular value decomposition computed by DGESVF. Matrix A is:
* *
| 1.0 4.0 |
| 2.0 5.0 |
| 3.0 6.0 |
* *
and where B is:
* *
| 7.0 10.0 |
| 8.0 11.0 |
| 9.0 12.0 |
* *
On output, matrix UTB is overwritten.
| Note: | This example corresponds to Example 4 of DGESVF on page "Example 4". |
V LDV UB LDUB NB S X LDX M N TAU
| | | | | | | | | | |
CALL DGESVS( V , 3 , UB , 3 , 2 , S , X , 2 , 3 , 2 , TAU )
* *
| 0.922 -0.386 |
V = | -0.386 -0.922 |
| . . |
* *
* *
| -1.310 -2.321 |
UB = | -13.867 -18.963 |
| . . |
* *
S = (0.773, 9.508)
TAU = 0.5171D-14
* *
X = | -1.000 -2.000 |
| 2.000 3.000 |
* *
These subroutines compute the minimal norm linear least squares solution of
AX is congruent to B, using a QR decomposition with
column pivoting.
| A, B, X, rn, tau, aux | Subroutine |
| Short-precision real | SGELLS |
| Long-precision real | DGELLS |
| Fortran | CALL SGELLS | DGELLS (iopt, a, lda, b, ldb, x, ldx, rn, tau, m, n, nb, k, aux, naux) |
| C and C++ | sgells | dgells (iopt, a, lda, b, ldb, x, ldx, rn, tau, m, n, nb, k, aux, naux); |
| PL/I | CALL SGELLS | DGELLS (iopt, a, lda, b, ldb, x, ldx, rn, tau, m, n, nb, k, aux, naux); |
If iopt = 0, X is computed.
If iopt = 1, X and the Euclidean Norm of the residual vectors are computed.
Specified as: a fullword integer; iopt = 0 or 1.
Specified as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 116.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing numbers of the data type indicated in Table 116. On output, the contents of aux are overwritten.
If naux = 0 and error 2015 is unrecoverable, SGELLS and DGELLS dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, It must have the following values:
naux >= 3n+max(n, nb) for SGELLS
naux >= [ceiling(2.5n)+max(n, nb)] for DGELLS
If k <> 0, the nb column vectors of X contain minimal norm least squares solutions for nb distinct linear least squares problems. The elements in each solution vector correspond to the original columns of A.
If k = 0, the nb column vectors of X are set to 0.
Returned as: an ldx by (at least) nb array, containing numbers of the data type indicated in Table 116.
If iopt = 0 or k = 0, rn is not used in the computation.
If iopt = 1, rni is the Euclidean Norm of the residual vector for the linear least squares problem defined by the i-th column vector of B.
Returned as: a one-dimensional array of (at least) nb, containing numbers of the data type indicated in Table 116.
See references [44], [59], and [72] for additional guidance on determining suitable values for tau.
The minimal norm linear least squares solution of AX is congruent to B is computed using a QR decomposition with column pivoting, where:
Optionally, the Euclidean Norms of the residual vectors can be computed. Following are the steps involved in finding the minimal norm linear least squares solution of AX is congruent to B. A is decomposed, using Householder transformations and column pivoting, into the following form:
where:
k is the first index, where:
If k = n, the minimal norm linear least squares solution is obtained by solving RX = QTB and reordering X to correspond to the original columns of A.
If k < n, R has the following form:
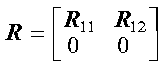
To find the minimal norm linear least squares solution, it is necessary to zero the submatrix R12 using Householder transformations. See references [44], [59], and [72]. If m or n is equal to 0, no computation is performed. These algorithms have a tendency to generate underflows that may hurt overall performance. The system default is to mask underflow, which improves the performance of these subroutines.
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
None
This example solves the underdetermined system AX is congruent to B. On output, A and B are overwritten. DUMMY is used as a placeholder for argument rn, which is not used in the computation.
IOPT A LDA B LDB X LDX RN TAU M N NB K AUX NAUX
| | | | | | | | | | | | | | |
CALL DGELLS( 0 , A , 2 , B , 2 , X , 3 , DUMMY , TAU , 2 , 3 , 1 , K , AUX , 11 )
* *
A = | 1.0 2.0 2.0 |
| 2.0 4.0 5.0 |
* *
* *
B = | 1.0 |
| 4.0 |
* *
TAU = 0.0
* *
| -0.600 |
X = | -1.200 |
| 2.000 |
* *
K = 2
This example solves the overdetermined system AX is congruent to B. On output, A and B are overwritten. DUMMY is used as a placeholder for argument rn, which is not used in the computation.
IOPT A LDA B LDB X LDX RN TAU M N NB K AUX NAUX
| | | | | | | | | | | | | | |
CALL DGELLS( 0 , A , 3 , B , 3 , X , 2 , DUMMY , TAU , 3 , 2 , 2 , K , AUX , 7 )
* *
| 1.0 4.0 |
A = | 2.0 5.0 |
| 3.0 6.0 |
* *
* *
| 7.0 10.0 |
B = | 8.0 11.0 |
| 9.0 12.0 |
* *
TAU = 0.0
* *
X = | -1.000 -2.000 |
| 2.000 3.000 |
* *
K = 2
This example solves the overdetermined system AX is congruent to B and computes the Euclidean Norms of the residual vectors. On output, A and B are overwritten.
IOPT A LDA B LDB X LDX RN TAU M N NB K AUX NAUX
| | | | | | | | | | | | | | |
CALL DGELLS( 1 , A , 3 , B , 3 , X , 2 , RN , TAU , 3 , 2 , 2 , K , AUX , 7 )
* *
| 1.1 -4.3 |
A = | 2.0 -5.0 |
| 3.0 -6.0 |
* *
* *
| -7.0 10.0 |
B = | -8.0 11.0 |
| -9.0 12.0 |
* *
TAU = 0.0
* *
X = | 0.543 -1.360 |
| 1.785 -2.699 |
* *
* *
RN = | 0.196 |
| 0.275 |
* *
K = 2