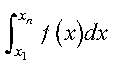
This section describes how to design and code the subf subroutine for use by the numerical quadrature subrutines.
For the Gaussian quadrature subroutines, you must supply a separate subroutine that is callable by ESSL. You specify the name of the subroutine in the subf argument. This subroutine name is selected by you. You should design the subf subroutine so it receives, as input, a tabulated set of points at which the integrand is evaluated, and it returns, as output, the values of the integrand evaluated at these points.
Depending on the numerical quadrature subroutine that you use, the subf subroutine is defined in one of the two following ways:
Examples of coding a subf subroutine in Fortran are provided for each subroutine in this chapter. Examples of coding a subf subroutine in C, C++, and PL/I are provided in "Example 1".
Depending on the programming language you use for your program that calls the numerical quadrature subroutines, you have a choice of one or more languages that you can use for writing subf. These rules and other langauge-related coding rules for setting up subf in your program are described in the following sections:
This section contains the numerical quadrature subroutine descriptions.
These subroutines approximate the integral of a real valued function
specified in tabular form, (xi,
yi) for i = 1, n. For
more than four points, an error estimate is returned along with the resulting
value.
| x, y, xyint, eest | Subroutine |
| Short-precision real | SPTNQ |
| Long-precision real | DPTNQ |
| Fortran | CALL SPTNQ | DPTNQ (x, y, n, xyint, eest) |
| C and C++ | sptnq | dptnq (x, y, n, xyint, eest); |
| PL/I | CALL SPTNQ | DPTNQ (x, y, n, xyint, eest); |
If n < 5, it is undefined and is set to 0.
If n >= 5, it is an estimate, eest, of the error in the integral, where xyint+eest tends to give a better approximation to the integral than xyint. For details, see references [26] and [58].
Returned as: a number of the data type indicated in Table 155.
The integral is approximated for a real valued function specified in tabular form, (xi, yi) for i = 1, n, where xi are distinct and sorted into ascending or descending order, and n >= 2. If yi = f(xi) for i = 1, n, then on output, xyint is an approximation to the integral of the following form:
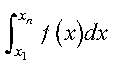
The algorithm used by this subroutine is based on the number of data points used in the computation, where:
For n >= 5, an estimate of the error eest is returned. For the method of Gill and Miller, it is shown that adding the estimate of the error eest to the result xyint often gives a better approximation to the integral than the result xyint by itself. For n < 5, an estimate of the error is not returned. In this case, a value of 0 is returned for eest. See references [58] and [26].
None
n < 2
This example shows the result of an integration, where the abscissas in X are sorted into ascending order.
X Y N XYINT EEST
| | | | |
CALL SPTNQ( X , Y , 10 , XYINT , EEST )
X = (0.0, 0.4, 1.0, 1.5, 2.1, 2.6, 3.0, 3.4, 3.9, 4.3)
Y = (1.0, 2.0, 3.0, 4.0, 5.0, 4.5, 4.0, 3.0, 3.5, 3.3)
XYINT = 15.137 EEST = -0.003
This example shows the result of an integration, where the abscissas in X are sorted into descending order.
X Y N XYINT EEST
| | | | |
CALL SPTNQ( X , Y , 10 , XYINT , EEST )
X = (4.3, 3.9, 3.4, 3.0, 2.6, 2.1, 1.5, 1.0, 0.4, 0.0)
Y = (3.3, 3.5, 3.0, 4.0, 4.5, 5.0, 4.0, 3.0, 2.0, 1.0)
XYINT = -15.137 EEST = 0.003
These functions approximate the integral of a real valued function over a
finite interval, using the Gauss-Legendre Quadrature method of specified
order.
| a, b, Result | Subroutine |
| Short-precision real | SGLNQ |
| Long-precision real | DGLNQ |
| Fortran | SGLNQ | DGLNQ (subf, a, b, n) |
| C and C++ | sglnq | dglnq (subf, a, b, n); |
| PL/I | SGLNQ | DGLNQ (subf, a, b, n); |
Specified as: subf must be declared as an external subroutine in you application program. It can be whatever name you choose.
The integral is approximated for a real valued function over a finite interval, using the Gauss-Legendre Quadrature method of specified order. The region of integration is from a to b. The method of order n is theoretically exact for integrals of the following form, where f is a polynomial of degree less than 2n:
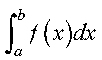
The method of order n is a good approximation when your integrand is closely approximated by a function of the form f(x), where f is a polynomial of degree less than 2n. See references [26] and [86]. The result is returned as the function value.
None
n is not an allowable value, as listed in the syntax for this argument.
This example shows how to compute the integral of the function f given by:
over the interval (0.0, 2.0), using the Gauss-Legendre method with 10 points:
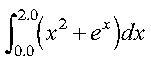
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN1 (T,Y,N) INTEGER*4 N REAL*4 T(*),Y(*) DO 1 I=1,N 1 Y(I)=T(I)**2+EXP(T(I)) RETURN END
EXTERNAL FUN1
.
.
.
SUBF A B N
| | | |
XINT = SGLNQ( FUN1 , 0.0 , 2.0 , 10 )
.
.
.
FUN1 =(see above)
XINT = 9.056
These functions approximate the integral of a real valued function of two
variables over a rectangular region, using the Gauss-Legendre Quadrature
method of specified order in each variable.
| a, b, c, d, Z, Result | Subroutine |
| Short-precision real | SGLNQ2 |
| Long-precision real | DGLNQ2 |
| Fortran | SGLNQ2 | DGLNQ2 (subf, a, b, n1, c, d, n2, z, ldz) |
| C and C++ | sglnq2 | dglnq2 (subf, a, b, n1, c, d, n2, z, ldz); |
| PL/I | SGLNQ2 | DGLNQ2 (subf, a, b, n1, c, d, n2, z, ldz); |
Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.
The integral:
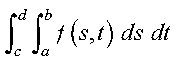
is approximated for a real valued function of two variables s and t, over a rectangular region, using the Gauss-Legendre Quadrature method of specified order in each variable. The region of integration is:
The method gives a good approximation when your integrand is closely approximated by a function of the form f(s, t), where f is a polynomial of degree less than 2(n1) for s and 2(n2) for t. See the function description for SGLNQ and DGLNQ--Numerical Quadrature Performed on a Function Using Gauss-Legendre Quadrature and references [26] and [86]. The result is returned as the function value.
To achieve optimal performance in this subroutine and in the functional evaluation, specify the first variable integrated in this subroutine as the variable having more points. The first variable integrated is the variable in the inner integral. For example, in the following integration, x is the first variable integrated:
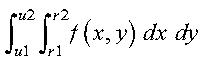
This is the suggested order of integration if the x variable has more points than the y variable. On the other hand, if the y variable has more points, you make y the first variable integrated.
Because the order of integration does not matter to the resulting approximation, you may be able to reverse the order that x and y are integrated and get better performance. This can be expressed as:
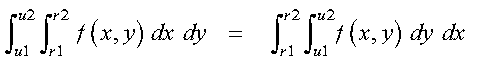
Results are mathematically equivalent. However, because the algorithm is computed in a different way, results may not be bitwise identical.
Table 158 shows how to assign your variables to the _GLNQ2 and subf arguments
for the x-y integration shown on the left and for the
y-x integration shown on the right. For examples of how to
do each of these, see "Example 1" and "Example 2".
Table 158. How to Assign Your Variables for x-y Integration Versus y-x Integration
_GLNQ2 and SUBF Arguments |
Variables for x-y Integration |
Variables for y-x Integration |
|---|---|---|
For _GLNQ2:
a
b
n1
c
d
n2
For subf:
s
t
n1
n2
|
r1 r2 (order for x) u1 u2 (order for y) x y (order for x) (order for y) |
u1 u2 (order for y) r1 r2 (order for x) y x (order for y) (order for x) |
None
This example shows how to compute the integral of the function f given by:
over the intervals (0.0, 2.0) for the first variable x and (-2.0, -1.0) for the second variable y, using the Gauss-Legendre method with 10 points in the x variable and 5 points in the y variable:
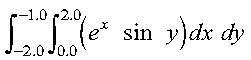
Because the variable x has more points, it is the first variable integrated. This allows the SGLNQ2 subroutine and the FUN1 evaluation to achieve optimal performance. Therefore, the x and y variables correspond to S and T in the FUN1 subroutine. Also, the x and y variables correspond to the A, B, N1 and C, D, N2 sets of arguments, respectively, for SGLNQ2.
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN1 (S,N1,T,N2,Z,LDZ) INTEGER*4 N1,N2,LDZ REAL*4 S(*),T(*),Z(LDZ,*) DO 1 J=1,N2 DO 2 I=1,N1 2 Z(I,J)=EXP(S(I))*SIN(T(J)) 1 CONTINUE RETURN END
| Note: |
The computation for this user-supplied subroutine FUN1 can also be
performed by using the following statements in place of the above DO loops,
using T1 and T2 as temporary storage areas:
. . . DO 1 I=1,N1 1 T1(I)=EXP(S(I)) DO 2 J=1,N2 2 T2(J)=SIN(T(J)) DO 3 J=1,N2 DO 4 I=1,N1 4 Z(I,J)=T1(I)*T2(J) 3 CONTINUE . . . |
When coding your application, this is the preferred technique. It reduces the number of evaluations performed and, therefore, provides better performance.
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in C as follows:
void fun1(s, n1, t, n2, z, ldz)
float *s, *t, *z;
int *n1, *n2, *ldz;
{
int i, j;
for(j = 0; j < *n2; ++j, z += *ldz)
{
for(i = 0; i < *n1; ++i)
z[i] = exp(s[i]) * sin(t[j]);
}
}
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in C++ as follows:
void fun1(float *s, int *n1, float *t, int *n2, float *z, int *ldz)
{
int i, j;
for(j = 0; j < *n2; ++j, z += *ldz)
{
for(i = 0; i < *n1; ++i)
z[i] = exp(s[i]) * sin(t[j]);
}
}
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in PL/I as follows:
FUN1: PROCEDURE(S,N1,T,N2,Z,LDZ) OPTIONS(FORTRAN,NOMAP);
DCL (N1,N2,LDZ,I,J) REAL FIXED BINARY(31,0);
DCL (S(10),T(10),Z(5,10)) REAL FLOAT DEC(16) ALIGNED CONNECTED;
DO J=1 TO N1;
DO I=1 TO N2;
Z(I,J)=EXP(S(J))*SIN(T(I));
END;
END;
RETURN;
END FUN1;
EXTERNAL FUN1
.
.
.
SUBF A B N1 C D N2 Z LDZ
| | | | | | | | |
XYINT = SGLNQ2( FUN1 , 0.0 , 2.0 , 10 , -2.0 , -1.0 , 5 , Z , 10 )
.
.
.
FUN1 =(see sections above) Z =(not relevant)
XYINT = -6.1108
This example shows how to reverse the order of integration of the variables x and y. It computes the integral of the function f given by:
over the intervals (0.0, 1.0) for the variable x and (0.0, 20.0) for the variable y, using the Gauss-Legendre method with 5 points in the x variable and 48 points in the y variable. Because the order of integration does not matter to the approximation:
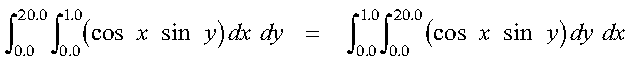
the variable y, having more points, is the first variable integrated (performing the integration shown on the right.) This allows the SGLNQ2 subroutine and the FUN1 evaluation to achieve optimal performance. Therefore, the x and y variables correspond to T and S in the FUN2 subroutine. Also, the x and y variables correspond to the C, D, N2 and A, B, N1 sets of arguments, respectively, for SGLNQ2.
The user-supplied subroutine FUN2, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN2 (S,N1,T,N2,Z,LDZ) INTEGER*4 N1,N2,LDZ REAL*4 S(*),T(*),Z(LDZ,*) DO 1 J=1,N2 DO 2 I=1,N1 2 Z(I,J)=COS(T(J))*SIN(S(I)) 1 CONTINUE RETURN END
| Note: | The same coding principles for achieving good performance that are noted in "Example 1" also apply to this user-supplied subroutine FUN2. |
EXTERNAL FUN2.
.
.
.
SUBF A B N1 C D N2 Z LDZ
| | | | | | | | |
YXINT = SGLNQ2( FUN2 , 0.0 , 20.0 , 48 , 0.0 , 1.0 , 5 , Z , 48 )
.
.
.
FUN2 =(see above) Z =(not relevant)
YXINT = 0.4981
These functions approximate the integral of a real valued function over a
semi-infinite interval, using the Gauss-Laguerre Quadrature method of
specified order.
| a, b, Result | Subroutine |
| Short-precision real | SGLGQ |
| Long-precision real | DGLGQ |
| Fortran | SGLGQ | DGLGQ (subf, a, b, n) |
| C and C++ | sglgq | dglgq (subf, a, b, n); |
| PL/I | SGLGQ | DGLGQ (subf, a, b, n); |
Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.
If b > 0, it is the lower limit of integration.
If b < 0, it is the upper limit of integration.
Specified as: a number of the data type indicated in Table 159.
The integral is approximated for a real valued function over a semi-infinite interval, using the Gauss-Laguerre Quadrature method of specified order. The region of integration is:
The method of order n is theoretically exact for integrals of the following form, where f is a polynomial of degree less than 2n:
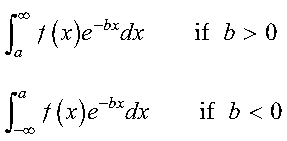
The method of order n is a good approximation when your integrand is closely approximated by a function of the form f(x)e-bx, where f is a polynomial of degree less than 2n. See references [26] and [86]. The result is returned as the function value.
None
This example shows how to compute the integral of the function f given by:
over the interval (-2.0, infinity), using the Gauss-Laguerre method with 20 points:
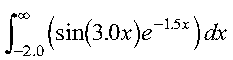
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN1 (T,Y,N) INTEGER*4 N REAL*4 T(*),Y(*) DO 1 I=1,N 1 Y(I)=SIN(3.0*T(I))*EXP(-1.5*T(I)) RETURN END
EXTERNAL FUN1
.
.
.
SUBF A B N
| | | |
XINT = SGLGQ( FUN1 , -2.0 , 1.5 , 20 )
.
.
.
FUN1 =(see above)
XINT = 5.891
This example shows how to compute the integral of the function f given by:
over the interval (-infinity, -2.0), using the Gauss-Laguerre method with 20 points:
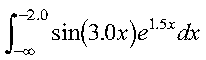
The user-supplied subroutine FUN2, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN2 (T,Y,N) INTEGER*4 N REAL*4 T(*),Y(*),TEMP DO 1 I=1,N 1 Y(I)=SIN(3.0*T(I))*EXP(1.5*T(I)) RETURN END
EXTERNAL FUN2
.
.
.
SUBF A B N
| | | |
XINT = SGLGQ( FUN2 , -2.0 , -1.5 , 20 )
.
.
.
FUN2 = (see above)
XINT = -0.011
These functions approximate the integral of a real valued function over a
semi-infinite interval, using the Gaussian-Rational quadrature method of
specified order.
| a, b, Result | Subroutine |
| Short-precision real | SGRAQ |
| Long-precision real | DGRAQ |
| Fortran | SGRAQ | DGRAQ (subf, a, b, n) |
| C and C++ | sgraq | dgraq (subf, a, b, n); |
| PL/I | SGRAQ | DGRAQ (subf, a, b, n); |
Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.
If a+b > 0, it is the lower limit of integration.
If a+b < 0, it is the upper limit of integration.
Specified as: a number of the data type indicated in Table 160.
The integral is approximated for a real valued function over a semi-infinite interval, using the Gauss-Rational quadrature method of specified order. The region of integration is:
The method of order n is theoretically exact for integrals of the following form, where f is a polynomial of degree less than 2n:
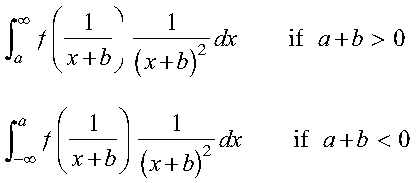
The method of order n is a good approximation when your integrand is closely approximated by a function of the following form, where f is a polynomial of degree less than 2n:
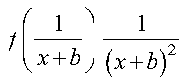
See references [26] and [86]. The result is returned as the function value to a Fortran, C, C++, or PL/I program.
None
This example shows how to compute the integral of the function f given by:
over the interval (-infinity, -2.0), using the Gauss-Rational method with 10 points:
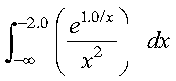
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN1 (T,Y,N)
INTEGER*4 N
REAL*4 T(*),Y(*),TEMP
DO 1 I=1,N
TEMP=1.0/T(I)
1 Y(I)=EXP(TEMP)*TEMP**2
RETURN
END
EXTERNAL FUN1
.
.
.
SUBF A B N
| | | |
XINT = SGRAQ( FUN1 , -2.0 , 0.0 , 10 )
.
.
.
FUN1 =(see above)
XINT = 0.393
This example shows how to compute the integral of the function f given by:
over the interval (4.0, infinity), using the Gauss-Rational method with 6 points:
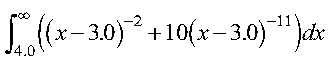
The user-supplied subroutine FUN2, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN2 (T,Y,N)
INTEGER*4 N
REAL*4 T(*),Y(*),TEMP
DO 1 I=1,N
TEMP=1.0/(T(I)-3.0)
1 Y(I)=TEMP**2+10.0*TEMP**11
RETURN
END
EXTERNAL FUN2
.
.
.
SUBF A B N
| | | |
XINT = SGRAQ( FUN2 , 4.0 , -3.0 , 6 )
.
.
.
FUN2 = (see above)
XINT = 2.00
These functions approximate the integral of a real valued function over the
entire real line, using the Gauss-Hermite Quadrature method of specified
order.
| a, b, Result | Subroutine |
| Short-precision real | SGHMQ |
| Long-precision real | DGHMQ |
| Fortran | SGHMQ | DGHMQ (subf, a, b, n) |
| C and C++ | sghmq | dghmq (subf, a, b, n); |
| PL/I | SGHMQ | DGHMQ (subf, a, b, n); |
Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.
The integral is approximated for a real valued function over the entire real line, using the Gauss-Hermite Quadrature method of specified order. The region of integration is from -infinity to infinity. The method of order n is theoretically exact for integrals of the following form, where f is a polynomial of degree less than 2n:
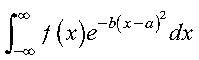
The method of order n is a good approximation when your integrand is closely approximated by a function of the following form, where f is a polynomial of degree less than 2n:
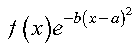
See references [26] and [86]. The result is returned as the function value to a Fortran, C, C++, or PL/I program.
None
This example shows how to compute the integral of the function f given by:
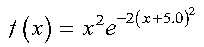
over the interval (-infinity, infinity), using the Gauss-Hermite method with 4 points:
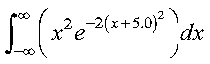
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:
SUBROUTINE FUN1 (T,Y,N) INTEGER*4 N REAL*4 T(*),Y(*) DO 1 I=1,N 1 Y(I)=T(I)**2*EXP(-2.0*(T(I)+5.0)**2) RETURN END
EXTERNAL FUN1
.
.
.
SUBF A B N
| | | |
XINT = SGHMQ( FUN1 , -5.0 , 2.0 , 4 )
.
.
.
FUN1 =(see above)
XINT = 31.646