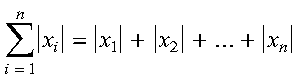
Compressed-matrix storage mode is generally applicable. It should be used when each row of the matrix contains approximately the same number of nonzero elements. However, if the matrix has a special form--that is, where the nonzero elements are concentrated along a few diagonals--compressed-diagonal storage mode gives improved performance.
This section contains the vector-scalar subprogram descriptions.
ISAMAX and IDAMAX find the position i of the first or last occurrence of a vector element having the maximum absolute value. ICAMAX and IZAMAX find the position i of the first or last occurrence of a vector element having the largest sum of the absolute values of the real and imaginary parts of the vector elements.
You get the position of the first or last occurrence of an element by
specifying positive or negative stride, respectively, for vector x.
Regardless of the stride, the position i is always relative to the
location specified in the calling sequence for vector x (in
argument x).
| x | Subprogram |
| Short-precision real | ISAMAX |
| Long-precision real | IDAMAX |
| Short-precision complex | ICAMAX |
| Long-precision complex | IZAMAX |
| Fortran | ISAMAX | IDAMAX | ICAMAX | IZAMAX (n, x, incx) |
| C and C++ | isamax | idamax | icamax | izamax (n, x, incx); |
| PL/I | ISAMAX | IDAMAX | ICAMAX | IZAMAX (n, x, incx); |
If incx >= 0, i is the position of the first occurrence.
If incx < 0, i is the position of the last occurrence.
Returned as: a fullword integer; 0 <= i <= n.
Declare the ISAMAX, IDAMAX, ICAMAX, and IZAMAX functions in your program as returning a fullword integer value.
ISAMAX and IDAMAX find the first element xk, where k is defined as the smallest index k, such that:
ICAMAX and IZAMAX find the first element xk, where k is defined as the smallest index k, such that:
By specifying a positive or negative stride for vector x, the first or last occurrence, respectively, is found in the array. The position i, returned as the value of the function, is always figured relative to the location specified in the calling sequence for vector x (in argument x). Therefore, depending on the stride specified for incx, i has the following values:
See reference [73]. The result is returned as a function value. If n is 0, then 0 is returned as the value of the function.
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
IMAX = ISAMAX( 9 , X , 1 )
X = (1.0, 2.0, 7.0, -8.0, -5.0, -10.0, -9.0, 10.0, 6.0)
IMAX = 6
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
IMAX = ISAMAX( 5 , X , 2 )
X = (1.0, . , 7.0, . , -5.0, . , -9.0, . , 6.0)
IMAX = 4
This example shows a vector, x, with a stride of 0.
N X INCX
| | |
IMAX = ISAMAX( 9 , X , 0 )
X = (1.0, . , . , . , . , . , . , . , .)
IMAX = 1
This example shows a vector, x, with a negative stride. Processing begins at element X(15), which is 2.0.
N X INCX
| | |
IMAX = ISAMAX( 8 , X , -2 )
X = (3.0, . , 5.0, . , -8.0, . , 6.0, . , 8.0, . ,
4.0, . , 8.0, . , 2.0)
IMAX = 7
This example shows a vector, x, containing complex numbers and having a stride of 1.
N X INCX
| | |
IMAX = ICAMAX( 5 , X , 1 )
X = ((9.0 , 2.0) , (7.0 , -8.0) , (-5.0 , -10.0) , (-4.0 , 10.0),
(6.0 , 3.0))
IMAX = 2
These subprograms find the position i of the first or last occurrence of a vector element having the minimum absolute value.
You get the position of the first or last occurrence of an element by
specifying positive or negative stride, respectively, for vector x.
Regardless of the stride, the position i is always relative to the
location specified in the calling sequence for vector x (in
argument x).
| x | Subprogram |
| Short-precision real | ISAMIN |
| Long-precision real | IDAMIN |
| Fortran | ISAMIN | IDAMIN (n, x, incx) |
| C and C++ | isamin | idamin (n, x, incx); |
| PL/I | ISAMIN | IDAMIN (n, x, incx); |
If incx >= 0, i is the position of the first occurrence.
If incx < 0, i is the position of the last occurrence.
Returned as: a fullword integer; 0 <= i <= n.
Declare the ISAMIN and IDAMIN functions in your program as returning a fullword integer value.
These subprograms find the first element xk, where k is defined as the smallest index k, such that:
By specifying a positive or negative stride for vector x, the first or last occurrence, respectively, is found in the array. The position i, returned as the value of the function, is always figured relative to the location specified in the calling sequence for vector x (in argument x). Therefore, depending on the stride specified for incx, i has the following values:
See reference [73]. The result is returned as a function value. If n is 0, then 0 is returned as the value of the function.
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
IMIN = ISAMIN( 6 , X , 1 )
X = (3.0, 4.0, 1.0, 8.0, 1.0, 3.0)
IMIN = 3
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
IMIN = ISAMIN( 4 , X , 2 )
X = (-3.0, . , -9.0, . , -8.0, . , 3.0)
IMIN = 1
This example shows a vector, x, with a positive stride and two elements with the minimum absolute value. The position of the first occurrence is returned.
N X INCX
| | |
IMIN = ISAMIN( 4 , X , 2 )
X = (2.0, . , -1.0, . , 4.0, . , 1.0)
IMIN = 2
This example shows a vector, x, with a negative stride and two elements with the minimum absolute value. The position of the last occurrence is returned. Processing begins at element X(7), which is 1.0.
N X INCX
| | |
IMIN = ISAMIN( 4 , X , -2 )
X = (2.0, . , -1.0, . , 4.0, . , 1.0)
IMIN = 4
These subprograms find the position i of the first or last occurrence of a vector element having the maximum value.
You get the position of the first or last occurrence of an element by
specifying positive or negative stride, respectively, for vector x.
Regardless of the stride, the position i is always relative to the
location specified in the calling sequence for vector x (in
argument x).
| x | Subprogram |
| Short-precision real | ISMAX |
| Long-precision real | IDMAX |
| Fortran | ISMAX | IDMAX (n, x, incx) |
| C and C++ | ismax | idmax (n, x, incx); |
| PL/I | ISMAX | IDMAX (n, x, incx); |
If incx >= 0, i is the position of the first occurrence.
If incx < 0, i is the position of the last occurrence.
Returned as: a fullword integer; 0 <= i <= n.
Declare the ISMAX and IDMAX functions in your program as returning a fullword integer value.
These subprograms find the first element xk, where k is defined as the smallest index k, such that:
By specifying a positive or negative stride for vector x, the first or last occurrence, respectively, is found in the array. The position i, returned as the value of the function, is always figured relative to the location specified in the calling sequence for vector x (in argument x). Therefore, depending on the stride specified for incx, i has the following values:
See reference [73]. The result is returned as a function value. If n is 0, then 0 is returned as the value of the function.
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
IMAX = ISMAX( 6 , X , 1 )
X = (3.0, 4.0, 1.0, 8.0, 1.0, 8.0)
IMAX = 4
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
IMAX = ISMAX( 4 , X , 2 )
X = (-3.0, . , 9.0, . , -8.0, . , 3.0)
IMAX = 2
This example shows a vector, x, with a positive stride and two elements with the maximum value. The position of the first occurrence is returned.
N X INCX
| | |
IMAX = ISMAX( 4 , X , 2 )
X = (2.0, . , 4.0, . , 4.0, . , 1.0)
IMAX = 2
This example shows a vector, x, with a negative stride and two elements with the maximum value. The position of the last occurrence is returned. Processing begins at element X(7), which is 1.0.
N X INCX
| | |
IMAX = ISMAX( 4 , X , -2 )
X = (2.0, . , 4.0, . , 4.0, . , 1.0)
IMAX = 3
These subprograms find the position i of the first or last occurrence of a vector element having the minimum value.
You get the position of the first or last occurrence of an element by
specifying positive or negative stride, respectively, for vector x.
Regardless of the stride, the position i is always relative to the
location specified in the calling sequence for vector x (in
argument x).
| x | Subprogram |
| Short-precision real | ISMIN |
| Long-precision real | IDMIN |
| Fortran | ISMIN | IDMIN (n, x, incx) |
| C and C++ | ismin | idmin (n, x, incx); |
| PL/I | ISMIN | IDMIN (n, x, incx); |
If incx >= 0, i is the position of the first occurrence.
If incx < 0, i is the position of the last occurrence.
Returned as: a fullword integer; 0 <= i <= n.
Declare the ISMIN and IDMIN functions in your program as returning a fullword integer value.
These subprograms find the first element xk, where k is defined as the smallest index k, such that:
By specifying a positive or negative stride for vector x, the first or last occurrence, respectively, is found in the array. The position i, returned as the value of the function, is always figured relative to the location specified in the calling sequence for vector x (in argument x). Therefore, depending on the stride specified for incx, i has the following values:
See reference [73]. The result is returned as a function value. If n is 0, then 0 is returned as the value of the function.
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
IMIN = ISMIN( 6 , X , 1 )
X = (3.0, 4.0, 1.0, 8.0, 1.0, 3.0)
IMIN = 3
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
IMIN = ISMIN( 4 , X , 2 )
X = (-3.0, . , -9.0, . , -8.0, . , 3.0)
IMIN = 2
This example shows a vector, x, with a positive stride and two elements with the minimum value. The position of the first occurrence is returned. Processing begins at element X(7), which is 1.0.
N X INCX
| | |
IMIN = ISMIN( 4 , X , 2 )
X = (2.0, . , 1.0, . , 4.0, . , 1.0)
IMIN = 2
This example shows a vector, x, with a negative stride and two elements with the minimum value. The position of the last occurrence is returned. Processing begins at element X(7), which is 1.0.
N X INCX
| | |
IMIN = ISMIN( 4 , X , -2 )
X = (2.0, . , 1.0, . , 4.0, . , 1.0)
IMIN = 4
SASUM and DASUM compute the sum of the absolute values of the elements in
vector x. SCASUM and DZASUM compute the sum of the absolute values
of the real and imaginary parts of the elements in vector x.
| x | Result | Subprogram |
| Short-precision real | Short-precision real | SASUM |
| Long-precision real | Long-precision real | DASUM |
| Short-precision complex | Short-precision real | SCASUM |
| Long-precision complex | Long-precision real | DZASUM |
| Fortran | SASUM | DASUM | SCASUM | DZASUM (n, x, incx) |
| C and C++ | sasum | dasum | scasum | dzasum (n, x, incx); |
| PL/I | SASUM | DASUM | SCASUM | DZASUM (n, x, incx); |
Declare this function in your program as returning a value of the type indicated in Table 40.
SASUM and DASUM compute the sum of the absolute values of the elements of x, which is expressed as follows:
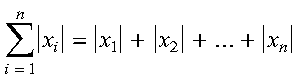
SCASUM and DZASUM compute the sum of the absolute values of the real and imaginary parts of the elements of x, which is expressed as follows:
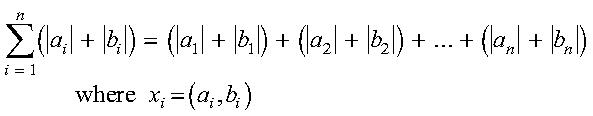
See reference [73]. The result is returned as a function value. If n is 0, then 0.0 is returned as the value of the function. For SASUM and SCASUM, intermediate results are accumulated in long precision.
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
SUMM = SASUM( 7 , X , 1 )
X = (1.0, -3.0, -6.0, 7.0, 5.0, 2.0, -4.0)
SUMM = 28.0
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
SUMM = SASUM( 4 , X , 2 )
X = (1.0, . , -6.0, . , 5.0, . , -4.0)
SUMM = 16.0
This example shows a vector, x, with negative stride. Processing begins at element X(7), which is -4.0.
N X INCX
| | |
SUMM = SASUM( 4 , X , -2 )
X = (1.0, . , -6.0, . , 5.0, . , -4.0)
SUMM = 16.0
This example shows a vector, x, with a stride of 0. The result in SUMM is nx1.
N X INCX
| | |
SUMM = SASUM( 7 , X , 0 )
X = (-2.0, . , . , . , . , . , .)
SUMM = 14.0
This example shows a vector, x, containing complex numbers and having a stride of 1.
N X INCX
| | |
SUMM = SCASUM( 5 , X , 1 )
X = ((1.0, 2.0), (-3.0, 4.0), (5.0, -6.0 ), (-7.0, -8.0),
(9.0, 10.0))
SUMM = 55.0
These subprograms perform the following computation, using the scalar alpha and vectors x and y:
| alpha, x, y | Subprogram |
| Short-precision real | SAXPY |
| Long-precision real | DAXPY |
| Short-precision complex | CAXPY |
| Long-precision complex | ZAXPY |
| Fortran | CALL SAXPY | DAXPY | CAXPY | ZAXPY (n, alpha, x, incx, y, incy) |
| C and C++ | saxpy | daxpy | caxpy | zaxpy (n, alpha, x, incx, y, incy); |
| PL/I | CALL SAXPY | DAXPY | CAXPY | ZAXPY (n, alpha, x, incx, y, incy); |
The computation is expressed as follows:
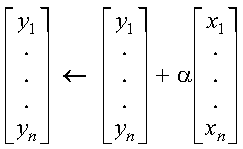
See reference [73]. If alpha or n is zero, no computation is performed. For CAXPY, intermediate results are accumulated in long precision.
None
n < 0
This example shows vectors x and y with positive strides.
N ALPHA X INCX Y INCY
| | | | | |
CALL SAXPY( 5 , 2.0 , X , 1 , Y , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)
Y = (3.0, . , 5.0, . , 7.0, . , 9.0, . , 11.0)
This example shows vectors x and y having strides of opposite signs. For y, which has negative stride, processing begins at element Y(5), which is 1.0.
N ALPHA X INCX Y INCY
| | | | | |
CALL SAXPY( 5 , 2.0 , X , 1 , Y , -1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Y = (15.0, 12.0, 9.0, 6.0, 3.0)
This example shows a vector, x, with 0 stride. Vector x is treated like a vector of length n, all of whose elements are the same as the single element in x.
N ALPHA X INCX Y INCY
| | | | | |
CALL SAXPY( 5 , 2.0 , X , 0 , Y , 1 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Y = (7.0, 6.0, 5.0, 4.0, 3.0)
This example shows how SAXPY can be used to compute a scalar value. In this case, vectors x and y contain scalar values and the strides for both vectors are 0. The number of elements to be processed, n, is 1.
N ALPHA X INCX Y INCY
| | | | | |
CALL SAXPY( 1 , 2.0 , X , 0 , Y , 0 )
X = (1.0)
Y = (5.0)
Y = (7.0)
This example shows how to use CAXPY, where vectors x and y contain complex numbers. In this case, vectors x and y have positive strides.
N ALPHA X INCX Y INCY
| | | | | |
CALL CAXPY( 3 ,ALPHA, X , 1 , Y , 2 )
ALPHA = (2.0, 3.0)
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
Y = ((1.0, 1.0 ), . , (0.0, 2.0), . , (5.0, 4.0))
Y = ((-3.0, 8.0), . , (4.0, 8.0), . , (-4.0, 23.0))
These subprograms copy vector x to another vector, y:
| x, y | Subprogram |
| Short-precision real | SCOPY |
| Long-precision real | DCOPY |
| Short-precision complex | CCOPY |
| Long-precision complex | ZCOPY |
| Fortran | CALL SCOPY | DCOPY | CCOPY | ZCOPY (n, x, incx, y, incy) |
| C and C++ | scopy | dcopy | ccopy | zcopy (n, x, incx, y, incy); |
| PL/I | CALL SCOPY | DCOPY | CCOPY | ZCOPY (n, x, incx, y, incy); |
The copy is expressed as follows:
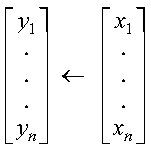
See reference [73]. If n is 0, no copy is performed.
None
n < 0
This example shows input vector x and output vector y with positive strides.
N X INCX Y INCY
| | | | |
CALL SCOPY( 5 , X , 1 , Y , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0)
This example shows how to obtain a reverse copy of the input vector x by specifying strides with the same absolute value, but with opposite signs, for input vector x and output vector y. For y, which has a negative stride, results are stored beginning at element Y(5).
N X INCX Y INCY
| | | | |
CALL SCOPY( 5 , X , 1 , Y , -1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
This example shows an input vector, x, with 0 stride. Vector x is treated like a vector of length n, all of whose elements are the same as the single element in x. This is a technique for replicating an element of a vector.
N X INCX Y INCY
| | | | |
CALL SCOPY( 5 , X , 0 , Y , 1 )
X = (13.0)
Y = (13.0, 13.0, 13.0, 13.0, 13.0)
This example shows input vector x and output vector y, containing complex numbers and having positive strides.
N X INCX Y INCY
| | | | |
CALL CCOPY( 4 , X , 1 , Y , 2 )
X = ((1.0, 1.0), (2.0, 2.0), (3.0, 3.0), (4.0, 4.0))
Y = ((1.0, 1.0), . , (2.0, 2.0), . , (3.0, 3.0), . ,
(4.0, 4.0))
SDOT, DDOT, CDOTU, and ZDOTU compute the dot product of vectors x and y:
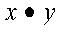
CDOTC and ZDOTC compute the dot product of the complex conjugate of vector x with vector y:
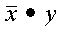
| x, y, Result | Subprogram |
| Short-precision real | SDOT |
| Long-precision real | DDOT |
| Short-precision complex | CDOTU and CDOTC |
| Long-precision complex | ZDOTU and ZDOTC |
| Fortran | SDOT | DDOT | CDOTU | ZDOTU | CDOTC | ZDOTC (n, x, incx, y, incy) |
| C and C++ | sdot | ddot | cdotu | zdotu | cdotc | zdotc (n, x, incx, y, incy); |
| PL/I | SDOT | DDOT | CDOTU | ZDOTU | CDOTC | ZDOTC (n, x, incx, y, incy); |
Declare this function in your program as returning a value of the data type indicated in Table 43.
SDOT, DDOT, CDOTU, and ZDOTU compute the dot product of the vectors x and y, which is expressed as follows:
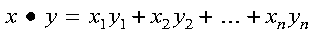
CDOTC and ZDOTC compute the dot product of the complex conjugate of vector x with vector y, which is expressed as follows:
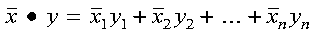
See reference [73]. The result is returned as a function value. If n is 0, then zero is returned as the value of the function.
For SDOT, CDOTU, and CDOTC, intermediate results are accumulated in long precision.
None
n < 0
This example shows how to compute the dot product of two vectors, x and y, having strides of 1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 1 , Y , 1 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, 8.0, 7.0, -6.0, 5.0)
DOTT = (9.0 + 16.0 - 21.0 - 24.0 + 25.0) = 5.0
This example shows how to compute the dot product of a vector, x, with a stride of 1, and a vector, y, with a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 1 , Y , 2 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, . , 7.0, . , 5.0, . , -3.0, . , 1.0)
DOTT = (9.0 + 14.0 - 15.0 - 12.0 + 5.0) = 1.0
This example shows how to compute the dot product of a vector, x, with a negative stride, and a vector, y, with a stride greater than 1. For x, processing begins at element X(5), which is 5.0.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , -1 , Y , 2 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, . , 7.0, . , 5.0, . , -3.0, . , 1.0)
DOTT = (45.0 + 28.0 - 15.0 - 6.0 + 1.0) = 53.0
This example shows how to compute the dot product of a vector, x, with a stride of 0, and a vector, y, with a stride of 1. The result in DOTT is x1(y1+...+yn).
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 0 , Y , 1 )
X = (1.0, . , . , . , .)
Y = (9.0, 8.0, 7.0, -6.0, 5.0)
DOTT = (1.0) × (9.0 + 8.0 + 7.0 - 6.0 + 5.0) = 23.0
This example shows how to compute the dot product of two vectors, x and y, with strides of 0. The result in DOTT is nx1y1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 0 , Y , 0 )
X = (1.0, . , . , . , .)
Y = (9.0, . , . , . , .)
DOTT = (5) × (1.0) × (9.0) = 45.0
This example shows how to compute the dot product of two vectors, x and y, containing complex numbers, where x has a stride of 1, and y has a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = CDOTU( 3 , X , 1 , Y , 2 )
X = ((1.0, 2.0), (3.0, -4.0), (-5.0, 6.0))
Y = ((10.0, 9.0), . , (-6.0, 5.0), . , (2.0, 1.0))
DOTT = ((10.0 - 18.0 - 10.0) - (18.0 - 20.0 + 6.0),
(9.0 + 15.0 - 5.0) + (20.0 + 24.0 + 12.0))
= (-22.0, 75.0)
This example shows how to compute the dot product of the conjugate of a vector, x, with vector y, both containing complex numbers, where x has a stride of 1, and y has a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = CDOTC( 3 , X , 1 , Y , 2 )
X = ((1.0, 2.0), (3.0, -4.0), (-5.0, 6.0))
Y = ((10.0, 9.0), . , (-6.0, 5.0), . , (2.0, 1.0))
DOTT = ((10.0 - 18.0 - 10.0) + (18.0 - 20.0 + 6.0),
(9.0 + 15.0 - 5.0) - (20.0 + 24.0 + 12.0))
= (-14.0, -37.0)
These subprograms compute SAXPY or DAXPY, respectively, n times:
where each alphai is a scalar value, contained in the
vector a, and each xi and
yi are vectors, contained in vectors (or
matrices) x and y, respectively. For an explanation of
the SAXPY and DAXPY computations, see SAXPY, DAXPY, CAXPY, and ZAXPY--Multiply a Vector X by a Scalar, Add to a Vector Y, and Store in the Vector Y.
| a, x, y | Subprogram |
| Short-precision real | SNAXPY |
| Long-precision real | DNAXPY |
| Fortran | CALL SNAXPY | DNAXPY (n, m, a, inca, x, incxi, incxo, y, incyi, incyo) |
| C and C++ | snaxpy | dnaxpy (n, m, a, inca, x, incxi, incxo, y, incyi, incyo); |
| PL/I | CALL SNAXPY | DNAXPY (n, m, a, inca, x, incxi, incxo, y, incyi, incyo); |
Vector y must have no common elements with vector a or vector x; otherwise, results are unpredictable. See "Concepts".
The SAXPY or DAXPY computations:
are performed n times. This is expressed as follows:
where each alphai is a scalar value, contained in the vector a, and each xi and yi are vectors, contained in vectors (or matrices) x and y, respectively.
Each computation of SAXPY or DAXPY on page SAXPY, DAXPY, CAXPY, and ZAXPY--Multiply a Vector X by a Scalar, Add to a Vector Y, and Store in the Vector Y uses the length of the xi and yi vectors, m, for its input argument, n. It also uses the strides for the inner loop, incxi and incyi, for its parameters incx and incy, respectively. See "Function" for a description of how the computation is done.
The outer loop of the SNAXPY or DNAXPY computation uses the strides of inca, incxo, and incyo to locate the elements in a and vectors in x and y for each i-th computation. These are:
If m or n is 0, no computation is performed.
None
This example shows vectors, contained in matrices, with the stride of the inner loops incxi and incyi equal to 1.
N M A INCA X INCXI INCXO Y INCYI INCYO
| | | | | | | | | |
CALL SNAXPY( 3 , 4 , A , 1 , X , 1 , 10 , Y , 1 , 5 )
A = (3.0, 2.0, 4.0)
* *
| 1.0 4.0 3.0 |
| 2.0 3.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 1.0 1.0 |
X = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 1.0 3.0 |
| 3.0 2.0 4.0 |
Y = | 2.0 3.0 2.0 |
| 1.0 4.0 1.0 |
| . . . |
* *
* *
| 7.0 9.0 15.0 |
| 9.0 8.0 20.0 |
Y = | 11.0 7.0 10.0 |
| 13.0 6.0 5.0 |
| . . . |
* *
This example shows vectors, contained in matrices, with a stride of the inner loop incxi greater than 1.
N M A INCA X INCXI INCXO Y INCYI INCYO
| | | | | | | | | |
CALL SNAXPY( 3 , 4 , A , 1 , X , 2 , 10 , Y , 1 , 5 )
A = (3.0, 2.0, 4.0)
* *
| 1.0 4.0 3.0 |
| . . . |
| 2.0 3.0 4.0 |
| . . . |
X = | 3.0 2.0 2.0 |
| . . . |
| 4.0 1.0 1.0 |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 1.0 3.0 |
| 3.0 2.0 4.0 |
Y = | 2.0 3.0 2.0 |
| 1.0 4.0 1.0 |
| . . . |
* *
Y =(same as output Y in Example 1)
This example shows vectors, contained in matrices, with a negative stride, incyi, for the inner loop.
N M A INCA X INCXI INCXO Y INCYI INCYO
| | | | | | | | | |
CALL SNAXPY( 3 , 4 , A , 1 , X , 1 , 10 , Y , -1 , 5 )
A = (3.0, 2.0, 4.0)
* *
| 1.0 4.0 3.0 |
| 2.0 3.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 1.0 1.0 |
X = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
* *
| 1.0 4.0 1.0 |
| 2.0 3.0 2.0 |
Y = | 3.0 2.0 4.0 |
| 4.0 1.0 3.0 |
| . . . |
* *
* *
| 13.0 6.0 5.0 |
| 11.0 7.0 10.0 |
Y = | 9.0 8.0 20.0 |
| 7.0 9.0 15.0 |
| . . . |
* *
This example shows vectors, contained in matrices, with a negative stride, inca, for vector a. For vector a, processing begins at element A(5), which is 3.0.
N M A INCA X INCXI INCXO Y INCYI INCYO
| | | | | | | | | |
CALL SNAXPY( 3 , 4 , A , -2 , X , 1 , 10 , Y , 1 , 5 )
A = (4.0, . , 2.0, . , 3.0)
* *
| 1.0 4.0 3.0 |
| 2.0 3.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 1.0 1.0 |
X = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 1.0 3.0 |
| 3.0 2.0 4.0 |
Y = | 2.0 3.0 2.0 |
| 1.0 4.0 1.0 |
| . . . |
* *
Y =(same as output Y in Example 1)
These subprograms compute one of the following special dot products
n times:
| si <-- xi * yi | Store positive dot product |
|
| si <-- -xi * yi | Store negative dot product |
|
| si <-- si+xi * yi | Accumulate positive dot product |
|
| si <-- si-xi * yi | Accumulate negative dot product |
|
|
|
|
where each si is an element in vector
s, and each xi and
yi are vectors contained in vectors (or
matrices) x and y, respectively.
| s, x, y | Subprogram |
| Short-precision real | SNDOT |
| Long-precision real | DNDOT |
| Fortran | CALL SNDOT | DNDOT (n, m, s, incs, isw, x, incxi, incxo, y, incyi, incyo) |
| C and C++ | sndot | dndot (n, m, s, incs, isw, x, incxi, incxo, y, incyi, incyo); |
| PL/I | CALL SNDOT | DNDOT (n, m, s, incs, isw, x, incxi, incxo, y, incyi, incyo); |
If isw = 3 or 4, si is used in the computation (input value specified.)
Specified as: a one-dimensional array of (at least) length 1+(n-1)|incs|, containing numbers of the data type indicated in Table 45.
If isw = 1, si <-- xi * yi
If isw = 2, si <-- -xi * yi
If isw = 3, si <-- si + xi * yi
If isw = 4, si <-- si - xi * yi
Specified as: a fullword integer. Its value must be 1, 2, 3, or 4.
If isw = 1, si <-- xi * yi
If isw = 2, si <-- -xi * yi
If isw = 3, si <-- si + xi * yi
If isw = 4, si <-- si - xi * yi
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 45.
The four possible computations that can be performed by these
subprograms are:
| si <-- xi * yi | Store positive dot product |
|
| si <-- -xi * yi | Store negative dot product |
|
| si <-- si+xi * yi | Accumulate positive dot product |
|
| si <-- si-xi * yi | Accumulate negative dot product |
|
|
|
|
where each si is a scalar element in the vector s of length n, and each of the n xi and yi vectors of length m are contained in vectors (or matrices) x and y, respectively. Each computation uses the dot product, which is expressed:
where ui and vi are elements of xi and yi, respectively. To find the elements for the computation, it uses:
If m or n is 0, no computation is performed. For SNDOT, intermediate results are accumulated in long precision.
None
This example shows a store positive dot product computation using vectors with positive strides.
N M S INCS ISW X INCXI INCXO Y INCYI INCYO
| | | | | | | | | | |
CALL SNDOT( 3 , 4 , S , 1 , 1 , X , 1 , 4 , Y , 1 , 4 )
* *
| 1.0 2.0 3.0 |
X = | 2.0 3.0 4.0 |
| 3.0 4.0 5.0 |
| 4.0 5.0 6.0 |
* *
* *
| 4.0 3.0 2.0 |
Y = | 3.0 2.0 1.0 |
| 2.0 1.0 4.0 |
| 1.0 4.0 3.0 |
* *
S = (20.0, 36.0, 48.0)
This example shows a store negative dot product computation using vectors with positive and negative strides.
N M S INCS ISW X INCXI INCXO Y INCYI INCYO
| | | | | | | | | | |
CALL SNDOT( 3 , 4 , S , -1 , 2 , X , 2 , 10 , Y , -1 , 6 )
* *
| 1.0 2.0 3.0 |
| . . . |
| 2.0 3.0 4.0 |
| . . . |
X = | 3.0 4.0 5.0 |
| . . . |
| 4.0 5.0 6.0 |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 3.0 2.0 |
| 3.0 2.0 1.0 |
Y = | 2.0 1.0 4.0 |
| 1.0 4.0 3.0 |
| . . . |
| . . . |
* *
S = (-42.0, -34.0, -30.0)
This example shows an accumulative positive dot product using vectors with positive and negative strides.
N M S INCS ISW X INCXI INCXO Y INCYI INCYO
| | | | | | | | | | |
CALL SNDOT( 3 , 4 , S , 1 , 3 , X , -2 , 10 , Y , 2 , 10 )
S = (2.0, 5.0, 8.0)
* *
| 1.0 2.0 3.0 |
| . . . |
| 2.0 3.0 4.0 |
| . . . |
X = | 3.0 4.0 5.0 |
| . . . |
| 4.0 5.0 6.0 |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 3.0 2.0 |
| . . . |
| 3.0 2.0 1.0 |
| . . . |
Y = | 2.0 1.0 4.0 |
| . . . |
| 1.0 4.0 3.0 |
| . . . |
| . . . |
| . . . |
* *
S = (32.0, 39.0, 50.0)
This example shows an accumulative negative dot product using vectors with positive and negative strides.
N M S INCS ISW X INCXI INCXO Y INCYI INCYO
| | | | | | | | | | |
CALL SNDOT( 3 , 4 , S , -1 , 4 , X , 1 , 6 , Y , 2 , 10 )
S = (3.0, 6.0, 9.0)
* *
| 1.0 2.0 3.0 |
| 2.0 3.0 4.0 |
X = | 3.0 4.0 5.0 |
| 4.0 5.0 6.0 |
| . . . |
| . . . |
* *
* *
| 4.0 3.0 2.0 |
| . . . |
| 3.0 2.0 1.0 |
| . . . |
Y = | 2.0 1.0 4.0 |
| . . . |
| 1.0 4.0 3.0 |
| . . . |
| . . . |
| . . . |
* *
S = (-45.0, -30.0, -11.0)
These subprograms compute the Euclidean length (l2
norm) of vector x, with scaling of input to avoid destructive
underflow and overflow.
| x | Result | Subprogram |
| Short-precision real | Short-precision real | SNRM2 |
| Long-precision real | Long-precision real | DNRM2 |
| Short-precision complex | Short-precision real | SCNRM2 |
| Long-precision complex | Long-precision real | DZNRM2 |
| Note: | If there is a possibility that your data will cause the computation to overflow or underflow, you should use these subroutines instead of SNORM2, DNORM2, CNORM2, and ZNORM2, because the intermediate computational results may exceed the maximum or minimum limits of the machine. "Notes" explains how to estimate whether your data will cause an overflow or underflow. |
| Fortran | SNRM2 | DNRM2 | SCNRM2 | DZNRM2 (n, x, incx) |
| C and C++ | snrm2 | dnrm2 | scnrm2 | dznrm2 (n, x, incx); |
| PL/I | SNRM2 | DNRM2 | SCNRM2 | DZNRM2 (n, x, incx); |
Declare this function in your program as returning a value of the data type indicated in Table 46.
The Euclidean length (l2 norm) of vector x is expressed as follows, with scaling of input to avoid destructive underflow and overflow:
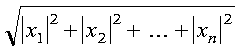
See reference [73]. The result is returned as the function value. If n is 0, then 0.0 is returned as the value of the function.
For SNRM2 and SCNRM2, the sum of the squares of the absolute values of the elements is accumulated in long precision. The square root of this long-precision sum is then computed and, if necessary, is unscaled.
Although these subroutines eliminate destructive underflow, nondestructive underflows may occur if the input elements differ greatly in magnitude. This does not affect accuracy, but it degrades performance. The system default is to mask underflow, which improves the performance of these subroutines.
None
n < 0
Workstations use workstation architecture precisions: ANSI/IEEE 32-bit and 64-bit binary floating-point format. The ranges are:
This example shows a vector, x, whose elements must be scaled to prevent overflow.
N X INCX
| | |
DNORM = DNRM2( 6 , X , 1 )
X = (0.68056D+200, 0.25521D+200, 0.34028D+200,
0.85071D+200, 0.25521D+200, 0.85071D+200)
DNORM = 0.1469D+201
This example shows a vector, x, whose elements must be scaled to prevent destructive underflow.
N X INCX
| | |
DNORM = DNRM2( 4 , X , 2 )
X = (0.10795D-200, . , 0.10795D-200, . , 0.10795D-200,
. , 0.10795D-200)
DNORM = 0.21590D-200
This example shows a vector, x, with a stride of 0. The result in SNORM is:
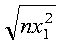
N X INCX
| | |
SNORM = SNRM2( 4 , X , 0 )
X = (4.0)
SNORM = 8.0
This example shows a vector, x, containing complex numbers, and whose elements must be scaled to prevent overflow.
N X INCX
| | |
DZNORM = DZNRM2( 3 , X , 1 )
X = ((0.68056D+200, 0.25521D+200), (0.34028D+200, 0.85071D+200),
(0.25521D+200, 0.85071D+200))
DZNORM = 0.1469D+201
This example shows a vector, x, containing complex numbers, and whose elements must be scaled to prevent destructive underflow.
N X INCX
| | |
DZNORM = DZNRM2( 2 , X , 2 )
X = ((0.10795D-200, 0.10795D-200), . ,
(0.10795D-200, 0.10795D-200))
DZNORM = 0.2159D-200
These subprograms compute the euclidean length (l2
norm) of vector x with no scaling of input.
| x | Result | Subprogram |
| Short-precision real | Short-precision real | SNORM2 |
| Long-precision real | Long-precision real | DNORM2 |
| Short-precision complex | Short-precision real | CNORM2 |
| Long-precision complex | Long-precision real | ZNORM2 |
| Fortran | SNORM2 | DNORM2 | CNORM2 | ZNORM2 (n, x, incx) |
| C and C++ | snorm2 | dnorm2 | cnorm2 | znorm2 (n, x, incx); |
| PL/I | SNORM2 | DNORM2 | CNORM2 | ZNORM2 (n, x, incx); |
The euclidean length (l2 norm) of vector x is expressed as follows with no scaling of input:
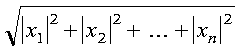
See reference [73]. The result is returned as the function value. If n is 0, then 0.0 is returned as the value of the function.
For SNORM2 and CNORM2, the sum of the squares of the absolute values of the elements is accumulated in long-precision. The square root of this long-precision sum is then computed.
This subroutine should not be used if the values in vector x do not conform to the restriction given in "Notes".
None
n < 0
This example shows a vector, x, with a stride of 1.
N X INCX
| | |
SNORM = SNORM2( 6 , X , 1 )
X = (3.0, 4.0, 1.0, 8.0, 1.0, 3.0)
SNORM = 10.0
This example shows a vector, x, with a stride greater than 1.
N X INCX
| | |
SNORM = SNORM2( 6 , X , 2 )
X = (3.0, . , 4.0, . , 1.0, . , 8.0, . , 1.0, . , 3.0)
SNORM = 10.0
This example shows a vector, x, with a stride of 0. The result in SNORM is:
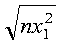
N X INCX
| | |
SNORM = SNORM2( 4 , X , 0 )
X = (4.0)
SNORM = 8.0
This example shows a vector, x, containing complex numbers and having a stride of 1.
N X INCX
| | |
CNORM = CNORM2( 3 , X , 1 )
X = ((3.0, 4.0), (1.0, 8.0), (-1.0, 3.0))
CNORM = 10.0
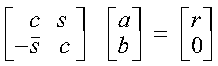
SROTG and DROTG construct a real Givens plane rotation, and CROTG and ZROTG construct a complex Givens plane rotation. The computations use rotational elimination parameters a and b. Values are returned for r, as well as the cosine c and the sine s of the angle of rotation. SROTG and DROTG also return a value for z.
| Note: | Throughout this description, the symbols r and z are used to represent two of the output values returned for this computation. It is important to note that the values for r and z are actually returned in the input-output arguments a and b, respectively, overwriting the original values passed in a and b. |
| a, b, r, s | c | z | Subprogram |
| Short-precision real | Short-precision real | Short-precision real | SROTG |
| Long-precision real | Long-precision real | Long-precision real | DROTG |
| Short-precision complex | Short-precision real | (No value returned) | CROTG |
| Long-precision complex | Long-precision real | (No value returned) | ZROTG |
| Fortran | CALL SROTG | DROTG | CROTG | ZROTG (a, b, c, s) |
| C and C++ | srotg | drotg | crotg | zrotg (a, b, c, s); |
| PL/I | CALL SROTG | DROTG | CROTG | ZROTG (a, b, c, s); |
For SROTG and DROTG:
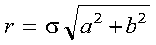
where:
For CROTG and ZROTG:
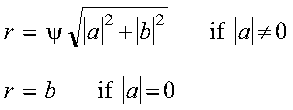
where:
Returned as: a number of the data type indicated in Table 48.
For SROTG and DROTG:
For CROTG and ZROTG: no value is returned, and the input value is not changed.
Returned as: a number of the data type indicated in Table 48.
For CROTG and ZROTG:
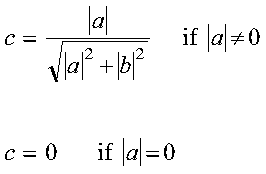
Returned as: a number of the data type indicated in Table 48.
For SROTG and DROTG:
For CROTG and ZROTG:
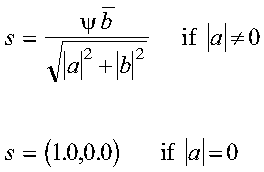
where psi = a/|a|
Returned as: a number of the data type indicated in Table 48.
In your C program, arguments a, b, c, and s must be passed by reference.
A real Givens plane rotation is constructed for values a and b by computing values for r, c, s, and z, where:
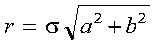
where:
c = a/r if r <> 0
c = 1 if r = 0
s = b/r if r <> 0
s = 0 if r = 0
z = s if |a| > |b|
z = 1/c if |a| <= |b| and c <> 0 and r <> 0
z = 1 if |a| <= |b| and c = 0 and r <> 0
z = 0 if r = 0
See reference [73].
Following are some important points about the computation:
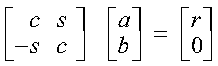
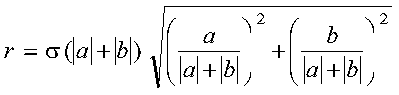
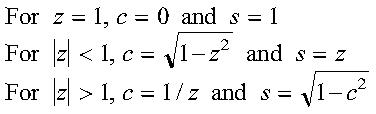
A complex Givens plane rotation is constructed for values a and b by computing values for r, c, and s, where:
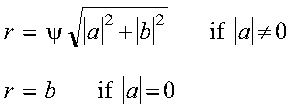
where:
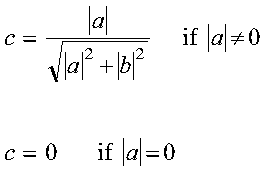
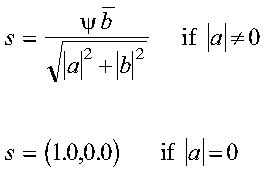
See reference [73].
Following are some important points about the computation:
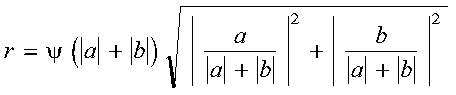
None
None
This example shows the construction of a real Givens plane rotation, where r is 0.
A B C S
| | | |
CALL SROTG( 0.0 , 0.0 , C , S )
A = 0.0 B = 0.0 C = 1.0 S = 0.0
This example shows the construction of a real Givens plane rotation, where c is 0.
A B C S
| | | |
CALL SROTG( 0.0 , 2.0 , C , S )
A = 2.0 B = 1.0 C = 0.0 S = 1.0
This example shows the construction of a real Givens plane rotation, where |b| > |a|.
A B C S
| | | |
CALL SROTG( 6.0 , -8.0 , C , S )
A = -10.0
_
B = -1.666
C = -0.6
S = 0.8
This example shows the construction of a real Givens plane rotation, where |a| > |b|.
A B C S
| | | |
CALL SROTG( 8.0 , 6.0 , C , S )
A = 10.0 B = 0.6 C = 0.8 S = 0.6
This example shows the construction of a complex Givens plane rotation, where |a| = 0.
A B C S
| | | |
CALL CROTG( A , B , C , S )
A = (0.0, 0.0)
B = (1.0, 0.0)
A = (1.0, 0.0) C = 0.0 S = (1.0, 0.0)
This example shows the construction of a complex Givens plane rotation, where |a| <> 0.
A B C S
| | | |
CALL CROTG( A , B , C , S )
A = (3.0, 4.0)
B = (4.0, 6.0)
A = (5.26, 7.02) C = 0.57 S = (0.82, -0.05)
SROT and DROT apply a real plane rotation to real vectors; CROT and ZROT
apply a complex plane rotation to complex vectors; and CSROT and ZDROT apply a
real plane rotation to complex vectors. The plane rotation is applied to
n points, where the points to be rotated are contained in vectors
x and y, and where the cosine and sine of the angle of
rotation are c and s, respectively.
| x, y | c | s | Subprogram |
| Short-precision real | Short-precision real | Short-precision real | SROT |
| Long-precision real | Long-precision real | Long-precision real | DROT |
| Short-precision complex | Short-precision real | Short-precision complex | CROT |
| Long-precision complex | Long-precision real | Long-precision complex | ZROT |
| Short-precision complex | Short-precision real | Short-precision real | CSROT |
| Long-precision complex | Long-precision real | Long-precision real | ZDROT |
| Fortran | CALL SROT | DROT | CROT | ZROT | CSROT | ZDROT (n, x, incx, y, incy, c, s) |
| C and C++ | srot | drot | crot | zrot | csrot | zdrot (n, x, incx, y, incy, c, s); |
| PL/I | CALL SROT | DROT | CROT | ZROT | CSROT | ZDROT (n, x, incx, y, incy, c, s); |
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 49.
For SROT, DROT, CSROT, and ZDROT:
For CROT and ZROT:
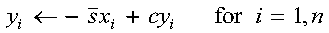
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 49.
The vectors x and y must have no common elements; otherwise, results are unpredictable. See "Concepts".
Applying a plane rotation to n points, where the points to be rotated are contained in vectors x and y, is expressed as follows, where c and s are the cosine and sine of the angle of rotation, respectively. For SROT, DROT, CSROT, and ZDROT:
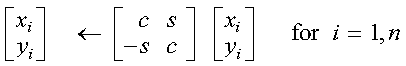
For CROT and ZROT:
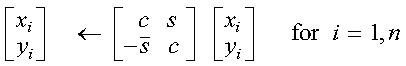
See references [54] and [73]. No computation is performed if n is 0 or if c is 1.0 and s is zero. For SROT, CROT, and CSROT, intermediate results are accumulated in long precision.
None
n < 0
This example shows how to apply a real plane rotation to real vectors x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 5 , X , 1 , Y , 2 , 0.5 , S )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-1.0, . , -2.0, . , -3.0, . , -4.0, . , -5.0)
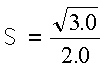
X = (-0.366, -0.732, -1.098, -1.464, -1.830) Y = (-1.366, -2.732, -4.098, -5.464, -6.830)
This example shows how to apply a real plane rotation to real vectors x and y having strides of opposite sign.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 5 , X , 1 , Y , -1 , 0.5 , S )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-5.0, -4.0, -3.0, -2.0, -1.0)
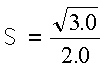
X =(same as output X in Example 1) Y = (-6.830, -5.464, -4.098, -2.732, -1.366)
This example shows how scalar values in vectors x and y can be processed by specifying 0 strides and the number of elements to be processed, n, equal to 1.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 1 , X , 0 , Y , 0 , 0.5 , S )
X = (1.0)
Y = (-1.0)
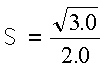
X = (-0.366) Y = (-1.366)
This example shows how to apply a complex plane rotation to complex vectors x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL CROT( 3 , X , 1 , Y , 2 , 0.5 , S )
X = ((1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
Y = ((-1.0, 5.0), . , (-2.0, 4.0), . , (-3.0, 3.0))
S = (0.75, 0.50)
X = ((-2.750, 4.250), (-2.500, 3.500), (-2.250, 2.750))
Y = ((-2.250, 1.500), . , (-4.000, 0.750), . ,
(-5.750, 0.000))
This example shows how to apply a real plane rotation to complex vectors x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL CSROT( 3 , X , 1 , Y , 2 , 0.5 , S )
X = ((1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
Y = ((-1.0, 5.0), . , (-2.0, 4.0), . , (-3.0, 3.0))
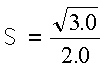
X = ((-0.366, 5.330), (-0.732, 4.964), (-1.098, 4.598))
Y = ((-1.366, 0.768), . , (-2.732, -0.598), . ,
(-4.098, -1.964))
These subprograms perform the following computation, using the scalar alpha and the vector x:
| alpha | x | Subprogram |
| Short-precision real | Short-precision real | SSCAL |
| Long-precision real | Long-precision real | DSCAL |
| Short-precision complex | Short-precision complex | CSCAL |
| Long-precision complex | Long-precision complex | ZSCAL |
| Short-precision real | Short-precision complex | CSSCAL |
| Long-precision real | Long-precision complex | ZDSCAL |
| Fortran | CALL SSCAL | DSCAL | CSCAL | ZSCAL | CSSCAL | ZDSCAL (n, alpha, x, incx) |
| C and C++ | sscal | dscal | cscal | zscal | csscal | zdscal (n, alpha, x, incx); |
| PL/I | CALL SSCAL | DSCAL | CSCAL | ZSCAL | CSSCAL | ZDSCAL (n, alpha, x, incx); |
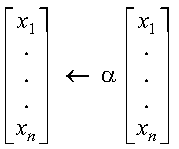
The fastest way in ESSL to zero out contiguous (stride 1) arrays is to call SSCAL or DSCAL, specifying incx = 1 and alpha = 0.
The computation is expressed as follows:
See reference [73]. If n is 0, no computation is performed. For CSCAL, intermediate results are accumulated in long precision.
None
n < 0
This example shows a vector, x, with a stride of 1.
N ALPHA X INCX
| | | |
CALL SSCAL( 5 , 2.0 , X , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
X = (2.0, 4.0, 6.0, 8.0, 10.0)
This example shows vector, x, with a stride greater than 1.
N ALPHA X INCX
| | | |
CALL SSCAL( 5 , 2.0 , X , 2 )
X = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0)
X = (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)
This example illustrates that when the strides for two similar computations (Example 1 and Example 3) have the same absolute value but have opposite signs, the output is the same. This example is the same as Example 1, except the stride for x is negative (-1). For performance reasons, it is better to specify the positive stride. For x, processing begins at element X(5), which is 5.0, and results are stored beginning at the same element.
N ALPHA X INCX
| | | |
CALL SSCAL( 5 , 2.0 , X , -1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
X = (2.0, 4.0, 6.0, 8.0, 10.0)
This example shows how SSCAL can be used to compute a scalar value. In this case, input vector x contains a scalar value, and the stride is 0. The number of elements to be processed, n, is 1.
N ALPHA X INCX
| | | |
CALL SSCAL( 1 , 2.0 , X , 0 )
X = (1.0)
X = (2.0)
This example shows a scalar, alpha, and a vector, x, containing complex numbers, where vector x has a stride of 1.
N ALPHA X INCX
| | | |
CALL CSCAL( 3 ,ALPHA, X , 1 )
ALPHA = (2.0, 3.0)
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
X = ((-4.0, 7.0), (4.0, 6.0), (-9.0, 19.0))
This example shows a scalar, alpha, containing a real number, and a vector, x, containing complex numbers, where vector x has a stride of 1.
N ALPHA X INCX
| | | |
CALL CSSCAL( 3 , 2.0 , X , 1 )
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
X = ((2.0, 4.0), (4.0, 0.0), (6.0, 10.0))
These subprograms interchange the elements of vectors x and y:
| x, y | Subprogram |
| Short-precision real | SSWAP |
| Long-precision real | DSWAP |
| Short-precision complex | CSWAP |
| Long-precision complex | ZSWAP |
| Fortran | CALL SSWAP | DSWAP | CSWAP | ZSWAP (n, x, incx, y, incy) |
| C and C++ | sswap | dswap | cswap | zswap (n, x, incx, y, incy); |
| PL/I | CALL SSWAP | DSWAP | CSWAP | ZSWAP (n, x, incx, y, incy); |
The elements of vectors x and y are interchanged as follows:
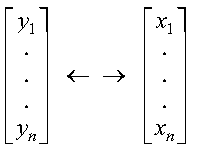
See reference [73]. If n is 0, no elements are interchanged.
None
n < 0
This example shows vectors x and y with positive strides.
N X INCX Y INCY
| | | | |
CALL SSWAP( 5 , X , 1 , Y , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-1.0, . , -2.0, . , -3.0, . , -4.0, . , -5.0)
X = (-1.0, -2.0, -3.0, -4.0, -5.0) Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0)
This example shows how to obtain output vectors x and y that are reverse copies of the input vectors y and x. You must specify strides with the same absolute value, but with opposite signs. For y, which has negative stride, processing begins at element Y(5), which is -5.0, and the results of the swap are stored beginning at the same element.
N X INCX Y INCY
| | | | |
CALL SSWAP( 5 , X , 1 , Y , -1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-1.0, -2.0, -3.0, -4.0, -5.0)
X = (-5.0, -4.0, -3.0, -2.0, -1.0) Y = (5.0, 4.0, 3.0, 2.0, 1.0)
This example shows how SSWAP can be used to interchange scalar values in vectors x and y by specifying 0 strides and the number of elements to be processed as 1.
N X INCX Y INCY
| | | | |
CALL SSWAP( 1 , X , 0 , Y , 0 )
X = (1.0)
Y = (-4.0)
X = (-4.0) Y = (1.0)
This example shows vectors x and y, containing complex numbers and having positive strides.
N X INCX Y INCY
| | | | |
CALL CSWAP( 4 , X , 1 , Y , 2 )
X = ((1.0, 6.0), (2.0, 7.0), (3.0, 8.0), (4.0, 9.0))
Y = ((-1.0, -1.0), . , (-2.0, -2.0), . , (-3.0, -3.0), . ,
(-4.0, -4.0))
X = ((-1.0, -1.0), (-2.0, -2.0), (-3.0, -3.0), (-4.0, -4.0))
Y = ((1.0, 6.0), . , (2.0, 7.0), . , (3.0, 8.0), . ,
(4.0, 9.0))
These subprograms perform the following computation, using vectors x, y, and z:
| x, y, z | Subprogram |
| Short-precision real | SVEA |
| Long-precision real | DVEA |
| Short-precision complex | CVEA |
| Long-precision complex | ZVEA |
| Fortran | CALL SVEA | DVEA | CVEA | ZVEA (n, x, incx, y, incy, z, incz) |
| C and C++ | svea | dvea | cvea | zvea (n, x, incx, y, incy, z, incz); |
| PL/I | CALL SVEA | DVEA | CVEA | ZVEA (n, x, incx, y, incy, z, incz); |
The computation is expressed as follows:
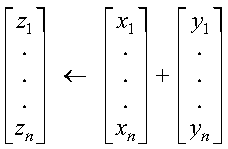
If n is 0, no computation is performed.
None
n < 0
This example shows vectors x, y, and z, with positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 1 , Y , 2 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)
Z = (2.0, 3.0, 4.0, 5.0, 6.0)
This example shows vectors x and y having strides of opposite sign, and an output vector z having a positive stride. For y, which has negative stride, processing begins at element Y(5), which is 1.0.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 1 , Y , -1 , Z , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)
This example shows a vector, x, with 0 stride and a vector, z, with negative stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x. For vector z, results are stored beginning in element Z(5).
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 0 , Y , 1 , Z , -1 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (2.0, 3.0, 4.0, 5.0, 6.0)
This example shows a vector, y, with 0 stride. y is treated like a vector of length n, all of whose elements are the same as the single element in y.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 1 , Y , 0 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (6.0, 7.0, 8.0, 9.0, 10.0)
This example shows the output vector, z, with 0 stride, where the vector x has positive stride, and the vector y has 0 stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 1 , Y , 0 , Z , 0 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (10.0)
This example shows the output vector z, with 0 stride, where the vector x has 0 stride, and the vector y has negative stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 5 , X , 0 , Y , -1 , Z , 0 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (6.0)
This example shows how SVEA can be used to compute a scalar value. In this case, vectors x and y contain scalar values. The strides of all vectors, x, y, and z, are 0. The number of elements to be processed, n, is 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEA( 1 , X , 0 , Y , 0 , Z , 0 )
X = (1.0)
Y = (5.0)
Z = (6.0)
This example shows vectors x and y, containing complex numbers and having positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL CVEA( 3 , X , 1 , Y , 2 , Z , 1 )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
Y = ((7.0, 8.0), . , (9.0, 10.0), . , (11.0, 12.0))
Z = ((8.0, 10.0), (12.0, 14.0), (16.0, 18.0))
These subprograms perform the following computation, using vectors x, y, and z:
| x, y, z | Subprogram |
| Short-precision real | SVES |
| Long-precision real | DVES |
| Short-precision complex | CVES |
| Long-precision complex | ZVES |
| Fortran | CALL SVES | DVES | CVES | ZVES (n, x, incx, y, incy, z, incz) |
| C and C++ | sves | dves | cves | zves (n, x, incx, y, incy, z, incz); |
| PL/I | CALL SVES | DVES | CVES | ZVES (n, x, incx, y, incy, z, incz); |
The computation is expressed as follows:
If n is 0, no computation is performed.
None
n < 0
This example shows vectors x, y, and z, with positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 1 , Y , 2 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)
Z = (0.0, 1.0, 2.0, 3.0, 4.0)
This example shows vectors x and y having strides of opposite sign, and an output vector z having a positive stride. For y, which has negative stride, processing begins at element Y(5), which is 1.0.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 1 , Y , -1 , Z , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (0.0, . , 0.0, . , 0.0, . , 0.0, . , 0.0)
This example shows a vector, x, with 0 stride, and a vector, z, with negative stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x. For vector z, results are stored beginning in element Z(5).
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 0 , Y , 1 , Z , -1 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (0.0, -1.0, -2.0, -3.0, -4.0)
This example shows a vector, y, with 0 stride. y is treated like a vector of length n, all of whose elements are the same as the single element in y.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 1 , Y , 0 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (-4.0, -3.0, -2.0, -1.0, 0.0)
This example shows the output vector z, with 0 stride, where the vector x has positive stride, and the vector y has 0 stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 1 , Y , 0 , Z , 0 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (0.0)
This example shows the output vector z, with 0 stride, where the vector x has 0 stride, and the vector y has negative stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 5 , X , 0 , Y , -1 , Z , 0 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (-4.0)
This example shows how SVES can be used to compute a scalar value. In this case, vectors x and y contain scalar values. The strides of all vectors, x, y, and z, are 0. The number of elements to be processed, n, is 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVES( 1 , X , 0 , Y , 0 , Z , 0 )
X = (1.0)
Y = (5.0)
Z = (-4.0)
This example shows vectors x and y, containing complex numbers and having positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL CVES( 3 , X , 1 , Y , 2 , Z , 1 )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
Y = ((7.0, 8.0), . , (9.0, 10.0), . , (11.0, 12.0))
Z = ((-6.0, -6.0), (-6.0, -6.0), (-6.0, -6.0))
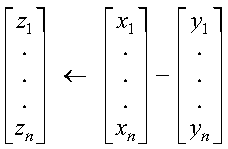
These subprograms perform the following computation, using vectors x, y, and z:
| x, y, z | Subprogram |
| Short-precision real | SVEM |
| Long-precision real | DVEM |
| Short-precision complex | CVEM |
| Long-precision complex | ZVEM |
| Fortran | CALL SVEM | DVEM | CVEM | ZVEM (n, x, incx, y, incy, z, incz) |
| C and C++ | svem | dvem | cvem | zvem (n, x, incx, y, incy, z, incz); |
| PL/I | CALL SVEM | DVEM | CVEM | ZVEM (n, x, incx, y, incy, z, incz); |
The computation is expressed as follows:
If n is 0, no computation is performed. For CVEM, intermediate results are accumulated in long precision (short-precision Multiply followed by a long-precision Add), with the final result truncated to short precision.
None
n < 0
This example shows vectors x, y, and z, with positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 1 , Y , 2 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)
Z = (1.0, 2.0, 3.0, 4.0, 5.0)
This example shows vectors x and y having strides of opposite sign, and an output vector z having a positive stride. For y, which has negative stride, processing begins at element Y(5), which is 1.0.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 1 , Y , -1 , Z , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (1.0, . , 4.0, . , 9.0, . , 16.0, . , 25.0)
This example shows a vector, x, with 0 stride, and a vector, z, with negative stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x. For vector z, results are stored beginning in element Z(5).
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 0 , Y , 1 , Z , -1 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (1.0, 2.0, 3.0, 4.0, 5.0)
This example shows a vector, y, with 0 stride. y is treated like a vector of length n, all of whose elements are the same as the single element in y.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 1 , Y , 0 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (5.0, 10.0, 15.0, 20.0, 25.0)
This example shows the output vector, z, with 0 stride, where the vector x has positive stride, and the vector y has 0 stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 1 , Y , 0 , Z , 0 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (25.0)
This example shows the output vector z, with 0 stride, where the vector x has 0 stride, and the vector y has negative stride. The number of elements to be processed, n, is greater than 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 5 , X , 0 , Y , -1 , Z , 0 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (5.0)
This example shows how SVEM can be used to compute a scalar value. In this case, vectors x and y contain scalar values. The strides of all vectors, x, y, and z, are 0. The number of elements to be processed, n, is 1.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL SVEM( 1 , X , 0 , Y , 0 , Z , 0 )
X = (1.0)
Y = (5.0)
Z = (5.0)
This example shows vectors x and y, containing complex numbers and having positive strides.
N X INCX Y INCY Z INCZ
| | | | | | |
CALL CVEM( 3 , X , 1 , Y , 2 , Z , 1 )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
Y = ((7.0, 8.0), . , (9.0, 10.0), . , (11.0, 12.0))
Z = ((-9.0, 22.0), (-13.0, 66.0), (-17.0, 126.0))
These subprograms perform the following computation, using the scalar alpha and vectors x and y:
| alpha | x, y | Subprogram |
| Short-precision real | Short-precision real | SYAX |
| Long-precision real | Long-precision real | DYAX |
| Short-precision complex | Short-precision complex | CYAX |
| Long-precision complex | Long-precision complex | ZYAX |
| Short-precision real | Short-precision complex | CSYAX |
| Long-precision real | Long-precision complex | ZDYAX |
| Fortran | CALL SYAX | DYAX | CYAX | ZYAX | CSYAX | ZDYAX (n, alpha, x, incx, y, incy) |
| C and C++ | syax | dyax | cyax | zyax | csyax | zdyax (n, alpha, x, incx, y, incy); |
| PL/I | CALL SYAX | DYAX | CYAX | ZYAX | CSYAX | ZDYAX (n, alpha, x, incx, y, incy); |
The computation is expressed as follows:
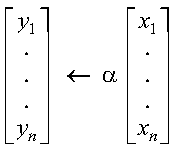
See reference [73]. If n is 0, no computation is performed. For CYAX, intermediate results are accumulated in long precision.
None
n < 0
This example shows vectors x and y with positive strides.
N ALPHA X INCX Y INCY
| | | | | |
CALL SYAX( 5 , 2.0 , X , 1 , Y , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)
This example shows vectors x and y that have strides of opposite signs. For y, which has negative stride, results are stored beginning in element Y(5).
N ALPHA X INCX Y INCY
| | | | | |
CALL SYAX( 5 , 2.0 , X , 1 , Y , -1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (10.0, 8.0, 6.0, 4.0, 2.0)
This example shows a vector, x, with 0 stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x.
N ALPHA X INCX Y INCY
| | | | | |
CALL SYAX( 5 , 2.0 , X , 0 , Y , 1 )
X = (1.0)
Y = (2.0, 2.0, 2.0, 2.0, 2.0)
This example shows how SYAX can be used to compute a scalar value. In this case both vectors x and y contain scalar values, and the strides for both vectors are 0. The number of elements to be processed, n, is 1.
N ALPHA X INCX Y INCY
| | | | | |
CALL SYAX( 1 , 2.0 , X , 0 , Y , 0 )
X = (1.0)
Y = (2.0)
This example shows a scalar, alpha, and vectors x and y, containing complex numbers, where both vectors have a stride of 1.
N ALPHA X INCX Y INCY
| | | | | |
CALL CYAX( 3 ,ALPHA, X , 1 , Y , 1 )
ALPHA = (2.0, 3.0)
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
Y = ((-4.0, 7.0), (4.0, 6.0), (-9.0, 19.0))
This example shows a scalar, alpha, containing a real number, and vectors x and y, containing complex numbers, where both vectors have a stride of 1.
N ALPHA X INCX Y INCY
| | | | | |
CALL CSYAX( 3 , 2.0 , X , 1 , Y , 1 )
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
Y = ((2.0, 4.0), (4.0, 0.0), (6.0, 10.0))
These subprograms perform the following computation, using the scalar alpha and vectors x, y, and z:
| alpha, x, y, z | Subprogram |
| Short-precision real | SZAXPY |
| Long-precision real | DZAXPY |
| Short-precision complex | CZAXPY |
| Long-precision complex | ZZAXPY |
| Fortran | CALL SZAXPY | DZAXPY | CZAXPY | ZZAXPY (n, alpha, x, incx, y, incy, z, incz) |
| C and C++ | szaxpy | dzaxpy | czaxpy | zzaxpy (n, alpha, x, incx, y, incy, z, incz); |
| PL/I | CALL SZAXPY | DZAXPY | CZAXPY | ZZAXPY (n, alpha, x, incx, y, incy, z, incz); |
The computation is expressed as follows:
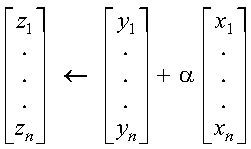
See reference [73]. If n is 0, no computation is performed. For CZAXPY, intermediate results are accumulated in long precision.
None
n < 0
This example shows vectors x and y with positive strides.
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL SZAXPY( 5 , 2.0 , X , 1 , Y , 2 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)
Z = (3.0, 5.0, 7.0, 9.0, 11.0)
This example shows vectors x and y having strides of opposite sign, and an output vector z having a positive stride. For y, which has negative stride, processing begins at element Y(5), which is 1.0.
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL SZAXPY( 5 , 2.0 , X , 1 , Y , -1 , Z , 2 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (3.0, . , 6.0, . , 9.0, . , 12.0, . , 15.0)
This example shows a vector, x, with 0 stride, and a vector, z, with negative stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x. For vector z, results are stored beginning in element Z(5).
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL SZAXPY( 5 , 2.0 , X , 0 , Y , 1 , Z , -1 )
X = (1.0)
Y = (5.0, 4.0, 3.0, 2.0, 1.0)
Z = (3.0, 4.0, 5.0, 6.0, 7.0)
This example shows a vector, y, with 0 stride. y is treated like a vector of length n, all of whose elements are the same as the single element in y.
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL SZAXPY( 5 , 2.0 , X , 1 , Y , 0 , Z , 1 )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (5.0)
Z = (7.0, 9.0, 11.0, 13.0, 15.0)
This example shows how SZAXPY can be used to compute a scalar value. In this case, vectors x and y contain scalar values. The strides of all vectors, x, y, and z, are 0. The number of elements to be processed, n, is 1.
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL SZAXPY( 1 , 2.0 , X , 0 , Y , 0 , Z , 0 )
X = (1.0)
Y = (5.0)
Z = (7.0)
This example shows vectors x and y, containing complex numbers and having positive strides.
N ALPHA X INCX Y INCY Z INCZ
| | | | | | | |
CALL CZAXPY( 3 ,ALPHA, X , 1 , Y , 2 , Z , 1 )
ALPHA = (2.0, 3.0)
X = ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))
Y = ((1.0, 1.0), . , (0.0, 2.0), . , (5.0, 4.0))
Z = ((-3.0, 8.0), (4.0, 8.0), (-4.0, 23.0))
This section contains the sparse vector-scalar subprogram descriptions.
These subprograms scatter the elements of sparse vector x,
stored in compressed-vector storage mode, into specified elements of sparse
vector y, stored in full-vector storage mode.
| x, y | Subprogram |
| Short-precision real | SSCTR |
| Long-precision real | DSCTR |
| Short-precision complex | CSCTR |
| Long-precision complex | ZSCTR |
| Fortran | CALL SSCTR | DSCTR | CSCTR | ZSCTR (nz, x, indx, y) |
| C and C++ | ssctr | dsctr | csctr | zsctr (nz, x, indx, y); |
| PL/I | CALL SSCTR | DSCTR | CSCTR | ZSCTR (nz, x, indx, y); |
Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.
Returned as: a one-dimensional array of (at least) length max(INDX(i)) for i = 1, nz, containing numbers of the data type indicated in Table 57.
The copy is expressed as follows:
where:
See reference [29]. If nz is 0, no copy is performed.
None
nz < 0
This example shows how to use SSCTR to copy a sparse vector x of length 5 into the following vector y, where the elements of array INDX are in ascending order:
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0 )
NZ X INDX Y
| | | |
CALL SSCTR( 5 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (1, 3, 4, 7, 10)
Y = (1.0, 2.0, 2.0, 3.0, 6.0, 10.0, 4.0, 8.0, 9.0, 5.0)
This example shows how to use SSCTR to copy a sparse vector x of length 5 into the following vector y, where the elements of array INDX are in random order:
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0 )
NZ X INDX Y
| | | |
CALL SSCTR( 5 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (4, 3, 1, 10, 7)
Y = (3.0, 2.0, 2.0, 1.0, 6.0, 10.0, 5.0, 8.0, 9.0, 4.0)
This example shows how to use CSCTR to copy a sparse vector x of length 3 into the following vector y, where the elements of array INDX are in random order:
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
NZ X INDX Y
| | | |
CALL CSCTR( 3 , X , INDX , Y )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX = (4, 1, 3)
Y = ((3.0, 4.0), (-2.0, 3.0), (5.0, 6.0), (1.0, 2.0))
These subprograms gather specified elements of vector y, stored
in full-vector storage mode, into sparse vector x, stored in
compressed-vector storage mode.
| x, y | Subprogram |
| Short-precision real | SGTHR |
| Long-precision real | DGTHR |
| Short-precision complex | CGTHR |
| Long-precision complex | ZGTHR |
| Fortran | CALL SGTHR | DGTHR | CGTHR | ZGTHR (nz, y, x, indx) |
| C and C++ | sgthr | dgthr | cgthr | zgthr (nz, y, x, indx); |
| PL/I | CALL SGTHR | DGTHR | CGTHR | ZGTHR (nz, y, x, indx); |
Specified as: a one-dimensional array of (at least) length max(INDX(i)) for i = 1, nz, containing numbers of the data type indicated in Table 58.
Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.
Returned as: a one-dimensional array of (at least) length nz, containing numbers of the data type indicated in Table 58.
The copy is expressed as follows:
xi <-- yINDX(i) for i = 1, nz
where:
See reference [29]. If nz is 0, no copy is performed.
None
nz < 0
This example shows how to use SGTHR to copy specified elements of a vector y into a sparse vector x of length 5, where the elements of array INDX are in ascending order.
NZ Y X INDX
| | | |
CALL SGTHR( 5 , Y , X , INDX )
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
INDX = (1, 3, 4, 7, 9)
X = (6.0, 4.0, 7.0, -2.0, 9.0)
This example shows how to use SGTHR to copy specified elements of a vector y into a sparse vector x of length 5, where the elements of array INDX are in random order. (Note that the element 0.0 occurs in output vector x. This does not produce an error.)
NZ Y X INDX
| | | |
CALL SGTHR( 5 , Y , X , INDX )
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
INDX = (4, 3, 1, 10, 7)
X = (7.0, 4.0, 6.0, 0.0, -2.0)
This example shows how to use CGTHR to copy specified elements of a vector, y, into a sparse vector, x, of length 3, where the elements of array INDX are in random order.
NZ Y X INDX
| | | |
CALL CGTHR( 3 , Y , X , INDX )
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
INDX = (4, 1, 3)
X = ((9.0, 0.0), (6.0, 5.0), (15.0, 4.0))
These subprograms gather specified elements of sparse vector y,
stored in full-vector storage mode, into sparse vector x, stored in
compressed-vector storage mode, and zero the same specified elements of vector
y.
| x, y | Subprogram |
| Short-precision real | SGTHRZ |
| Long-precision real | DGTHRZ |
| Short-precision complex | CGTHRZ |
| Long-precision complex | ZGTHRZ |
| Fortran | CALL SGTHRZ | DGTHRZ | CGTHRZ | ZGTHRZ (nz, y, x, indx) |
| C and C++ | sgthrz | dgthrz | cgthrz | zgthrz (nz, y, x, indx); |
| PL/I | CALL SGTHRZ | DGTHRZ | CGTHRZ | ZGTHRZ (nz, y, x, indx); |
Specified as: a one-dimensional array of (at least) length max(INDX(i)) for i = 1, nz, containing numbers of the data type indicated in Table 59.
Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 59.
Returned as: a one-dimensional array of (at least) length nz, containing numbers of the data type indicated in Table 59.
The copy is expressed as follows:
where:
See reference [29]. If nz is 0, no computation is performed.
None
nz < 0
This example shows how to use SGTHRZ to copy specified elements of a vector y into a sparse vector x of length 5, where the elements of array INDX are in ascending order.
NZ Y X INDX
| | | |
CALL SGTHRZ( 5 , Y , X , INDX )
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
INDX = (1, 3, 4, 7, 9)
Y = (0.0, 2.0, 0.0, 0.0, 6.0, 10.0, 0.0, 8.0, 0.0, 0.0) X = (6.0, 4.0, 7.0, -2.0, 9.0)
This example shows how to use SGTHRZ to copy specified elements of a vector y into a sparse vector x of length 5, where the elements of array INDX are in random order. (Note that the element 0.0 occurs in output vector x. This does not produce an error.)
NZ Y X INDX
| | | |
CALL SGTHRZ( 5 , Y , X , INDX )
Y = (6.0, 2.0, 4.0, 7.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
INDX = (4, 3, 1, 10, 7)
Y = (0.0, 2.0, 0.0, 0.0, 6.0, 10.0, 0.0, 8.0, 9.0, 0.0) X = (7.0, 4.0, 6.0, 0.0, -2.0)
This example shows how to use CGTHRZ to copy specified elements of a vector y into a sparse vector x of length 3, where the elements of array INDX are in random order.
NZ Y X INDX
| | | |
CALL CGTHRZ( 3 , Y , X , INDX )
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
INDX = (4, 1, 3)
Y = ((0.0, 0.0), (-2.0, 3.0), (0.0, 0.0), (0.0, 0.0)) X = ((9.0, 0.0), (6.0, 5.0), (15.0, 4.0))
These subprograms multiply sparse vector x, stored in
compressed-vector storage mode, by scalar alpha, add it to sparse vector
y, stored in full-vector storage mode, and store the result in
vector y.
| alpha, x, y | Subprogram |
| Short-precision real | SAXPYI |
| Long-precision real | DAXPYI |
| Short-precision complex | CAXPYI |
| Long-precision complex | ZAXPYI |
| Fortran | CALL SAXPYI | DAXPYI | CAXPYI | ZAXPYI (nz, alpha, x, indx, y) |
| C and C++ | saxpyi | daxpyi | caxpyi | zaxpyi (nz, alpha, x, indx, y); |
| PL/I | CALL SAXPYI | DAXPYI | CAXPYI | ZAXPYI (nz, alpha, x, indx, y); |
Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 60.
The computation is expressed as follows:
where:
See reference [29]. If alpha or nz is zero, no computation is performed. For SAXPYI and CAXPYI, intermediate results are accumulated in long-precision.
None
nz < 0
This example shows how to use SAXPYI to perform a computation using a sparse vector x of length 5, where the elements of array INDX are in ascending order.
NZ ALPHA X INDX Y
| | | | |
CALL SAXPYI( 5 , 2.0 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (1, 3, 4, 7, 10)
Y = (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
Y = (3.0, 5.0, 8.0, 9.0, 6.0, 10.0, 6.0, 8.0, 9.0, 10.0)
This example shows how to use SAXPYI to perform a computation using a sparse vector x of length 5, where the elements of array INDX are in random order.
NZ ALPHA X INDX Y
| | | | |
CALL SAXPYI( 5 , 2.0 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (4, 3, 1, 10, 7)
Y = (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
Y = (7.0, 5.0, 8.0, 5.0, 6.0, 10.0, 8.0, 8.0, 9.0, 8.0)
This example shows how to use CAXPYI to perform a computation using a sparse vector x of length 3, where the elements of array INDX are in random order.
NZ ALPHA X INDX Y
| | | | |
CALL CAXPYI( 3 , ALPHA , X , INDX , Y )
ALPHA = (2.0, 3.0)
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX = (4, 1, 3)
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
Y = ((0.0, 22.0), (-2.0, 3.0), (7.0, 31.0), (5.0, 7.0))
SDOTI, DDOTI, CDOTUI, and ZDOTUI compute the dot product of sparse vector x, stored in compressed-vector storage mode, and full vector y, stored in full-vector storage mode.
CDOTCI and ZDOTCI compute the dot product of the complex conjugate of
sparse vector x, stored in compressed-vector storage mode, and full
vector y, stored in full-vector storage mode.
| x, y, Result | Subprogram |
| Short-precision real | SDOTI |
| Long-precision real | DDOTI |
| Short-precision complex | CDOTUI |
| Long-precision complex | ZDOTUI |
| Short-precision complex | CDOTCI |
| Long-precision complex | ZDOTCI |
| Fortran | SDOTI | DDOTI | CDOTUI | ZDOTUI | CDOTCI | ZDOTCI (nz, x, indx, y) |
| C and C++ | sdoti | ddoti | cdotui | zdotui | cdotci | zdotci (nz, x, indx, y); |
| PL/I | SDOTI | DDOTI | CDOTUI | ZDOTUI | CDOTCI | ZDOTCI (nz, x, indx, y); |
Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.
Returned as: a number of the data type indicated in Table 61.
For SDOTI, DDOTI, CDOTUI, and ZDOTUI, the dot product computation is expressed as follows:
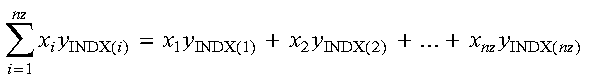
For CDOTCI and ZDOTCI, the dot product computation is expressed as follows:
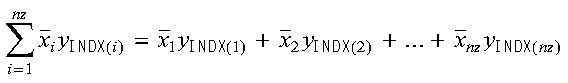
where:
x is a sparse vector, stored in compressed-vector storage mode.
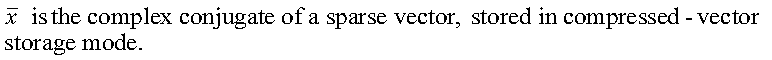
INDX is the indices array for sparse vector x.
y is a sparse vector, stored in full-vector storage mode.
See reference [29]. The result is returned as the function value. If nz is 0, then zero is returned as the value of the function.
For SDOTI, CDOTUI, and CDOTCI, intermediate results are accumulated in long-precision.
None
nz < 0
This example shows how to use SDOTI to compute a dot product using a sparse vector x of length 5, where the elements of array INDX are in ascending order.
NZ X INDX Y
| | | |
DOTT = SDOTI( 5 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (1, 3, 4, 7, 10)
Y = (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
DOTT = (1.0 + 8.0 + 9.0 -8.0 + 0.0) = 10.0
This example shows how to use SDOTI to compute a dot product using a sparse vector x of length 5, where the elements of array INDX are in random order.
NZ X INDX Y
| | | |
DOTT = SDOTI( 5 , X , INDX , Y )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
INDX = (4, 3, 1, 10, 7)
Y = (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)
DOTT = (3.0 + 8.0 + 3.0 + 0.0 -10.0) = 4.0
This example shows how to use CDOTUI to compute a dot product using a sparse vector x of length 3, where the elements of array INDX are in ascending order.
NZ X INDX Y
| | | |
DOTT = CDOTUI( 3 , X , INDX , Y )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX = (1, 3, 4)
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
DOTT = (70.0, 143.0)
This example shows how to use CDOTCI to compute a dot product using the complex conjugate of a sparse vector x of length 3, where the elements of array INDX are in random order.
NZ X INDX Y
| | | |
DOTT = CDOTCI( 3 , X , INDX , Y )
X = ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX = (4, 1, 3)
Y = ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))
DOTT = (146.0, -97.0)
This section contains the matrix-vector subprogram descriptions.
SGEMV and DGEMV compute the matrix-vector product for either a real general matrix or its transpose, using the scalars alpha and beta, vectors x and y, and matrix A or its transpose:
CGEMV and ZGEMV compute the matrix-vector product for either a complex general matrix, its transpose, or its conjugate transpose, using the scalars alpha and beta, vectors x and y, and matrix A, its transpose, or its conjugate transpose:
SGEMX and DGEMX compute the matrix-vector product for a real general matrix, using the scalar alpha, vectors x and y, and matrix A:
SGEMTX and DGEMTX compute the matrix-vector product for the transpose of a real general matrix, using the scalar alpha, vectors x and y, and the transpose of matrix A:
| alpha, beta, x, y, A | Subprogram |
| Short-precision real | SGEMV, SGEMX, and SGEMTX |
| Long-precision real | DGEMV, DGEMX, and DGEMTX |
| Short-precision complex | CGEMV |
| Long-precision complex | ZGEMV |
| Note: | SGEMV and DGEMV are Level 2 BLAS subroutines. It is suggested that these subroutines be used instead of SGEMX, DGEMX, SGEMTX, and DGEMTX, which are provided only for compatibility with earlier releases of ESSL. |
| Fortran | CALL SGEMV | DGEMV | CGEMV | ZGEMV (transa, m,
n, alpha, a, lda, x,
incx, beta, y, incy)
CALL SGEMX | DGEMX | SGEMTX | DGEMTX ( m, n, alpha, a, lda, x, incx, y, incy) |
| C and C++ | sgemv | dgemv | cgemv | zgemv (transa, m, n,
alpha, a, lda, x, incx,
beta, y, incy);
sgemx | dgemx | sgemtx | dgemtx ( m, n, alpha, a, lda, x, incx, y, incy); |
| PL/I | CALL SGEMV | DGEMV | CGEMV | ZGEMV (transa, m,
n, alpha, a, lda, x,
incx, beta, y, incy);
CALL SGEMX | DGEMX | SGEMTX | DGEMTX ( m, n, alpha, a, lda, x, incx, y, incy); |
If transa = 'N', A is used in the computation.
If transa = 'T', AT is used in the computation.
If transa = 'C', AH is used in the computation.
Specified as: a single character. It must be 'N', 'T', or 'C'.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it is the length of vector y.
For SGEMTX and DGEMTX, it is the length of vector x.
Specified as: a fullword integer; 0 <= m <= lda.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it is the length of vector x.
For SGEMTX and DGEMTX, it is the length of vector y.
Specified as: a fullword integer; n >= 0.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, A is used in the computation.
For SGEMTX and DGEMTX, AT is used in the computation.
| Note: | No data should be moved to form AT or AH; that is, the matrix A should always be stored in its untransposed form. |
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 62.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it has length n.
For SGEMTX and DGEMTX, it has length m.
Specified as: a one-dimensional array, containing numbers of the data type indicated in Table 62, where:
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it must have at least 1+(n-1)|incx| elements.
For SGEMTX and DGEMTX, it must have at least 1+(m-1)|incx| elements.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it has length m.
For SGEMTX and DGEMTX, it has length n.
Specified as: a one-dimensional array, containing numbers of the data type indicated in Table 62, where:
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it must have at least 1+(m-1)|incy| elements.
For SGEMTX and DGEMTX, it must have at least 1+(n-1)|incy| elements.
For SGEMV, DGEMV, CGEMV, and ZGEMV:
For SGEMX and DGEMX, it has length m.
For SGEMTX and DGEMTX, it has length n.
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 62.
The possible computations that can be performed by these subroutines are described in the following sections. Varying implementation techniques are used for this computation to improve performance. As a result, accuracy of the computational result may vary for different computations.
For SGEMV, CGEMV, SGEMX, and SGEMTX, intermediate results are accumulated in long precision. Occasionally, for performance reasons, these intermediate results are stored.
See references [34], [35], [38], [46], and [73]. No computation is performed if m or n is 0 or if alpha is zero and beta is one.
For SGEMV, DGEMV, CGEMV, and ZGEMV, the matrix-vector product for a general matrix:
is expressed as follows:
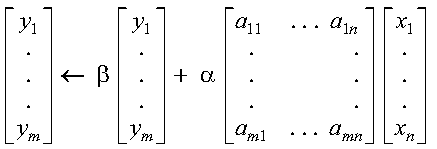
For SGEMX and DGEMX, the matrix-vector product for a real general matrix:
is expressed as follows:
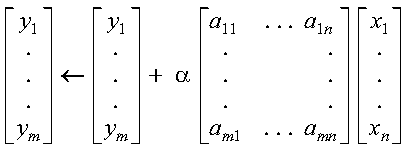
In these expressions:
For SGEMV, DGEMV, CGEMV and ZGEMV, the matrix-vector product for the transpose of a general matrix:
is expressed as follows:
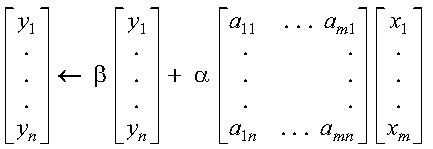
For SGEMTX and DGEMTX, the matrix-vector product for the transpose of a real general matrix:
is expressed as follows:
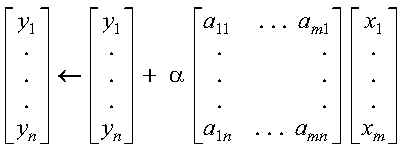
In these expressions:
For CGEMV and ZGEMV, the matrix-vector product for the conjugate transpose of a general matrix:
is expressed as follows:
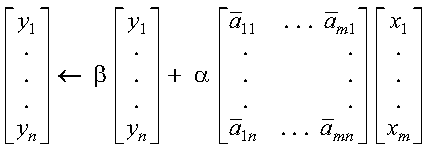
where:
Unable to allocate internal work area (for SGEMV, DGEMV, CGEMV, and ZGEMV).
None
This example shows the computation for TRANSA equal to 'N', where the real general matrix A is used in the computation. Because lda is 10 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=10 and F2-F1+1 >= 3. In this example, array A is declared as A(1:10,0:2).
TRANSA M N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL SGEMV( 'N' , 4 , 3 , 1.0 , A(1,0) , 10 , X , 1 , 1.0 , Y , 2 )
* *
| 1.0 2.0 3.0 |
| 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
A = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
X = (3.0, 2.0, 1.0) Y = (4.0, . , 5.0, . , 2.0, . , 3.0)
Y = (14.0, . , 19.0, . , 17.0, . , 20.0)
This example shows the computation for TRANSA equal to 'T', where the transpose of the real general matrix A is used in the computation. Array A must follow the same rules as given in Example 1. In this example, array A is declared as A(-1:8,1:3).
TRANSA M N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL SGEMV( 'T' , 4 , 3 , 1.0 , A(-1,1) , 10 , X , 1 , 2.0 , Y , 2 )
A =(same as input A in Example 1) X = (3.0, 2.0, 1.0, 4.0) Y = (1.0, . , 2.0, . , 3.0)
Y = (28.0, . , 24.0, . , 29.0)
This example shows the computation for TRANSA equal to 'N', where the complex general matrix A is used in the computation.
TRANSA M N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL CGEMV( 'N' , 5 , 3 , ALPHA , A , 10 , X , 1 , BETA , Y , 1 )
ALPHA = (1.0, 0.0)
* *
| (1.0, 2.0) (3.0, 5.0) (2.0, 0.0) |
| (2.0, 3.0) (7.0, 9.0) (4.0, 8.0) |
| (7.0, 4.0) (1.0, 4.0) (6.0, 0.0) |
| (8.0, 2.0) (2.0, 5.0) (8.0, 0.0) |
A = | (9.0, 1.0) (3.0, 6.0) (1.0, 0.0) |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
X = ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0))
BETA = (1.0, 0.0)
Y = ((1.0, 2.0), (4.0, 0.0), (1.0, -1.0), (3.0, 4.0),
(2.0, 0.0))
Y = ((12.0, 28.0), (24.0, 55.0), (10.0, 39.0), (23.0, 50.0),
(22.0, 44.0))
This example shows the computation for TRANSA equal to 'T', where the transpose of complex general matrix A is used in the computation. Because beta is zero, the result of the computation is alphaATx
TRANSA M N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL CGEMV( 'T' , 5 , 3 , ALPHA , A , 10 , X , 1 , BETA , Y , 1 )
ALPHA = (1.0, 0.0)
A =(same as input A in Example 3)
X = ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0), (3.0, 4.0),
(2.0, 0.0))
BETA = (0.0, 0.0)
Y =(not relevant)
Y = ((42.0, 67.0), (10.0, 87.0), (50.0, 74.0))
This example shows the computation for TRANSA equal to 'C', where the conjugate transpose of the complex general matrix A is used in the computation.
TRANSA M N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL CGEMV( 'C' , 5 , 3 , ALPHA , A , 10 , X , 1 , BETA , Y , 1 )
ALPHA = (-1.0, 0.0)
A =(same as input A in Example 3)
X = ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0), (3.0, 4.0),
(2.0, 0.0))
BETA = (1.0, 0.0)
Y = ((1.0, 2.0), (4.0, 0.0), (1.0, -1.0))
Y = ((-73.0, -13.0), (-74.0, 57.0), (-49.0, -11.0))
This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are positive. Because lda is 10 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=10 and F2-F1+1 >= 3. For this example, array A is declared as A(1:10,0:2).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMX( 4 , 3 , 1.0 , A(1,0) , 10 , X , 1 , Y , 2 )
* *
| 1.0 2.0 3.0 |
| 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
A = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
X = (3.0, 2.0, 1.0) Y = (4.0, . , 5.0, . , 2.0, . , 3.0)
Y = (14.0, . , 19.0, . , 17.0, . , 20.0)
This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are of opposite sign. For y, which has negative stride, processing begins at element Y(7), which is 4.0. Array A must follow the same rules as given in Example 6. For this example, array A is declared as A(-1:8,1:3).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMX( 4 , 3 , 1.0 , A(-1,1) , 10 , X , 1 , Y , -2 )
A =(same as input A in Example 6) X = (3.0, 2.0, 1.0) Y = (3.0, . , 2.0, . , 5.0, . , 4.0)
Y = (20.0, . , 17.0, . , 19.0, . , 14.0)
This example shows a matrix, A, contained in a larger array, A, and the first element of the matrix is not the first element of the array. Array A must follow the same rules as given in Example 6. For this example, array A is declared as A(1:10,1:3).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMX( 4 , 3 , 1.0 , A(5,1) , 10 , X , 1 , Y , 1 )
* *
| . . . |
| . . . |
| . . . |
| . . . |
A = | 1.0 2.0 3.0 |
| 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
| . . . |
| . . . |
* *
X = (3.0, 2.0, 1.0) Y = (4.0, 5.0, 2.0, 3.0)
Y = (14.0, 19.0, 17.0, 20.0)
This example shows a matrix, A, and an array, A, having the same number of rows. For this case, m and lda are equal. Because lda is 4 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=4 and F2-F1+1 >= 3. For this example, array A is declared as A(1:4,0:2).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMX( 4 , 3 , 1.0 , A(1,0) , 4 , X , 1 , Y , 1 )
* *
| 1.0 2.0 3.0 |
A = | 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
* *
X = (3.0, 2.0, 1.0)
Y = (4.0, 5.0, 2.0, 3.0)
Y = (14.0, 19.0, 17.0, 20.0)
This example shows a matrix, A, and an array, A, having the same number of rows. For this case, m and lda are equal. Because lda is 4 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=4 and F2-F1+1 >= 3. For this example, array A is declared as A(1:4,0:2).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMTX( 4 , 3 , 1.0 , A(1,0) , 4 , X , 1 , Y , 1 )
* *
| 1.0 2.0 3.0 |
A = | 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
* *
X = (3.0, 2.0, 1.0, 4.0)
Y = (1.0, 2.0, 3.0)
Y = (27.0, 22.0, 26.0)
This example shows a computation in which alpha is greater than 1. Array A must follow the same rules as given in Example 10. For this example, array A is declared as A(-1:2,1:3).
M N ALPHA A LDA X INCX Y INCY
| | | | | | | | |
CALL SGEMTX( 4 , 3 , 2.0 , A(-1,1) , 4 , X , 1 , Y , 1 )
A =(same as input A in Example 10) X = (3.0, 2.0, 1.0, 4.0) Y = (1.0, 2.0, 3.0)
Y = (53.0, 42.0, 49.0)
SGER, DGER, CGERU, and ZGERU compute the rank-one update of a general matrix, using the scalar alpha, matrix A, vector x, and the transpose of vector y:
CGERC and ZGERC compute the rank-one update of a general matrix, using the scalar alpha, matrix A, vector x, and the conjugate transpose of vector y:
| alpha, A, x, y | Subprogram |
| Short-precision real | SGER |
| Long-precision real | DGER |
| Short-precision complex | CGERU and CGERC |
| Long-precision complex | ZGERU and ZGERC |
| Note: | For compatibility with earlier releases of ESSL, you can use the names SGER1 and DGER1 for SGER and DGER, respectively. |
| Fortran | CALL SGER | DGER | CGERU | ZGERU | CGERC | ZGERC (m, n, alpha, x, incx, y, incy, a, lda) |
| C and C++ | sger | dger | cgeru | zgeru | cgerc | zgerc (m, n, alpha, x, incx, y, incy, a, lda); |
| PL/I | CALL SGER | DGER | CGERU | ZGERU | CGERC | ZGERC (m, n, alpha, x, incx, y, incy, a, lda); |
| Note: | No data should be moved to form yT or yH; that is, the vector y should always be stored in its untransposed form. |
Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 63.
Returned as: a two-dimensional array, containing numbers of the data type indicated in Table 63.
SGER, DGER, CGERU, and ZGERU compute the rank-one update of a general matrix:
where:
It is expressed as follows:
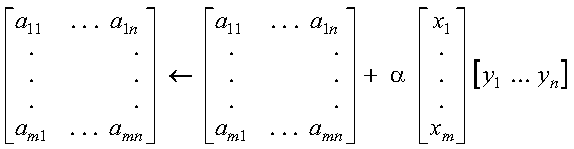
It can also be expressed as:
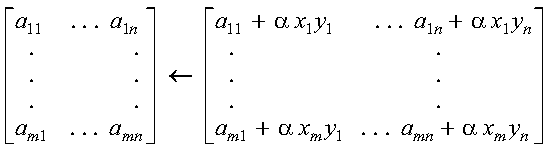
CGERC and ZGERC compute a slightly different rank-one update of a general matrix:
where:
It is expressed as follows:
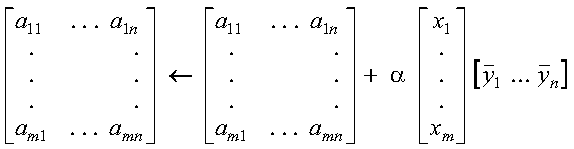
It can also be expressed as:
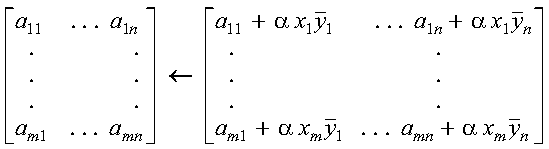
See references [34], [35], and [73]. No computation is performed if m, n, or alpha is zero. For CGERU and CGERC, intermediate results are accumulated in long precision. For SGER, intermediate results are accumulated in long precision on some platforms.
Unable to allocate internal work area.
None
This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are positive. Because lda is 10 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=10 and F2-F1+1 >= 3. For this example, array A is declared as A(1:10,0:2).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SGER( 4 , 3 , 1.0 , X , 1 , Y , 2 , A(1,0) , 10 )
X = (3.0, 2.0, 1.0, 4.0)
Y = (1.0, . , 2.0, . , 3.0)
* *
| 1.0 2.0 3.0 |
| 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
A = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
* *
| 4.0 8.0 12.0 |
| 4.0 6.0 10.0 |
| 4.0 4.0 5.0 |
| 8.0 10.0 13.0 |
A = | . . . |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are of opposite sign. For y, which has negative stride, processing begins at element Y(5), which is 1.0. Array A must follow the same rules as given in Example 1. For this example, array A is declared as A(-1:8,1:3).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SGER( 4 , 3 , 1.0 , X , 1 , Y , -2 , A(-1,1) , 10 )
X = (3.0, 2.0, 1.0, 4.0) Y = (3.0, . , 2.0, . , 1.0) A =(same as input A in Example 1)
A =(same as input A in Example 1)
This example shows a matrix, A, contained in a larger array, A, and the first element of the matrix is not the first element of the array. Array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,1:3).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SGER( 4 , 3 , 1.0 , X , 3 , Y , 1 , A(4,1) , 10 )
X = (3.0, . , . , 2.0, . , . , 1.0, . , . , 4.0)
Y = (1.0, 2.0, 3.0)
* *
| . . . |
| . . . |
| . . . |
| 1.0 2.0 3.0 |
A = | 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
| . . . |
| . . . |
| . . . |
* *
* *
| . . . |
| . . . |
| . . . |
| 4.0 8.0 12.0 |
A = | 4.0 6.0 10.0 |
| 4.0 4.0 5.0 |
| 8.0 10.0 13.0 |
| . . . |
| . . . |
| . . . |
* *
This example shows a matrix, A, and array, A, having the same number of rows. For this case, m and lda are equal. Because lda is 4 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=4 and F2-F1+1 >= 3. For this example, array A is declared as A(1:4,0:2).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SGER( 4 , 3 , 1.0 , X , 1 , Y , 1 , A(1,0) , 4 )
X = (3.0, 2.0, 1.0, 4.0)
Y = (1.0, 2.0, 3.0)
* *
| 1.0 2.0 3.0 |
A = | 2.0 2.0 4.0 |
| 3.0 2.0 2.0 |
| 4.0 2.0 1.0 |
* *
* *
| 4.0 8.0 12.0 |
A = | 4.0 6.0 10.0 |
| 4.0 4.0 5.0 |
| 8.0 10.0 13.0 |
* *
This example shows a computation in which scalar value for alpha is greater than 1. Array A must follow the same rules as given in Example 4. For this example, array A is declared as A(-1:2,1:3).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SGER( 4 , 3 , 2.0 , X , 1 , Y , 1 , A(-1,1) , 4 )
X = (3.0, 2.0, 1.0, 4.0) Y = (1.0, 2.0, 3.0) A =(same as input A in Example 4)
* *
| 7.0 14.0 21.0 |
A = | 6.0 10.0 16.0 |
| 5.0 6.0 8.0 |
| 12.0 18.0 25.0 |
* *
This example shows a rank-one update in which all data items contain complex numbers, and the transpose yT is used in the computation. Matrix A is contained in a larger array, A. The strides of vectors x and y are positive. The Fortran DIMENSION statement for array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,0:2).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL CGERU( 5 , 3 , ALPHA , X , 1 , Y , 1 , A(1,0) , 10 )
ALPHA = (1.0, 0.0)
X = ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0), (3.0, 4.0),
(2.0, 0.0))
Y = ((1.0, 2.0), (4.0, 0.0), (1.0, -1.0))
* *
| (1.0, 2.0) (3.0, 5.0) (2.0, 0.0) |
| (2.0, 3.0) (7.0, 9.0) (4.0, 8.0) |
| (7.0, 4.0) (1.0, 4.0) (6.0, 0.0) |
| (8.0, 2.0) (2.0, 5.0) (8.0, 0.0) |
A = | (9.0, 1.0) (3.0, 6.0) (1.0, 0.0) |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
* *
| (-2.0, 6.0) (7.0, 13.0) (5.0, 1.0) |
| (6.0, 11.0) (23.0, 9.0) (8.0, 4.0) |
| (6.0, 7.0) (5.0, 8.0) (8.0, 0.0) |
| (3.0, 12.0) (14.0, 21.0) (15.0, 1.0) |
A = | (11.0, 5.0) (11.0, 6.0) (3.0, -2.0) |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
This example shows a rank-one update in which all data items contain complex numbers, and the conjugate transpose yH is used in the computation. Matrix A is contained in a larger array, A. The strides of vectors x and y are positive. The Fortran DIMENSION statement for array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,0:2).
M N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL CGERC( 5 , 3 , ALPHA , X , 1 , Y , 1 , A(1,0) , 10 )
ALPHA = (1.0, 0.0)
X = ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0), (3.0, 4.0),
(2.0, 0.0))
Y = ((1.0, 2.0), (4.0, 0.0), (1.0, -1.0))
A =(same as input A in Example 6 )
* *
| (6.0, 2.0) (7.0, 13.0) (1.0, 3.0) |
| (6.0, -5.0) (23.0, 9.0) (8.0, 12.0) |
| (10.0, 3.0) (5.0, 8.0) (6.0, 2.0) |
| (19.0, 0.0) (14.0, 21.0) (7.0, 7.0) |
A = | (11.0, -3.0) (11.0, 6.0) (3.0, 2.0) |
| . . . |
| . . . |
| . . . |
| . . . |
| . . . |
* *
SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV compute the matrix-vector product for either a real symmetric matrix or a complex Hermitian matrix, using the scalars alpha and beta, matrix A, and vectors x and y:
SSLMX and DSLMX compute the matrix-vector product for a real symmetric matrix, using the scalar alpha, matrix A, and vectors x and y:
The following storage modes are used:
| alpha, beta, A, x, y | Subprogram |
| Short-precision real | SSPMV, SSYMV, and SSLMX |
| Long-precision real | DSPMV, DSYMV, and DSLMX |
| Short-precision complex | CHPMV and CHEMV |
| Long-precision complex | ZHPMV and ZHEMV |
| Note: | SSPMV and DSPMV are Level 2 BLAS subroutines. You should use these subroutines instead of SSLMX and DSLMX, which are provided only for compatibility with earlier releases of ESSL. |
| Fortran | CALL SSPMV | DSPMV | CHPMV | ZHPMV (uplo, n,
alpha, ap, x, incx, beta,
y, incy)
CALL SSYMV | DSYMV | CHEMV | ZHEMV (uplo, n, alpha, a, lda, x, incx, beta, y, incy) CALL SSLMX | DSLMX (n, alpha, ap, x, incx, y, incy) |
| C and C++ | sspmv | dspmv | chpmv | zhpmv (uplo, n, alpha,
ap, x, incx, beta, y,
incy);
ssymv | dsymv | chemv | zhemv (uplo, n, alpha, a, lda, x, incx, beta, y, incy); sslmx | dslmx (n, alpha, ap, x, incx, y, incy); |
| PL/I | CALL SSPMV | DSPMV | CHPMV | ZHPMV (uplo, n,
alpha, ap, x, incx, beta,
y, incy);
CALL SSYMV | DSYMV | CHEMV | ZHEMV (uplo, n, alpha, a, lda, x, incx, beta, y, incy); CALL SSLMX | DSLMX (n, alpha, ap, x, incx, y, incy); |
If uplo = 'U', A is stored in upper-packed or upper storage mode.
If uplo = 'L', A is stored in lower-packed or lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
For SSPMV and DSPMV, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.
For CHPMV and ZHPMV, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.
For SSLMX and DSLMX, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.
Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 64.
For SSYMV and DSYMV, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.
For CHEMV and ZHEMV, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 64.
For SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV, incx < 0 or incx > 0.
For SSLMX and DSLMX, incx can have any value.
These subroutines perform the computations described in the two sections below. See references [34], [35], and [73]. For SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV, if n is zero or if alpha is zero and beta is one, no computation is performed. For SSLMX and DSLMX, if n or alpha is zero, no computation is performed.
For SSLMX, SSPMV, SSYMV, CHPMV, and CHEMV, intermediate results are accumulated in long precision. However, several intermediate stores may occur for each element of the vector y.
These subroutines compute the matrix-vector product for either a real symmetric matrix or a complex Hermitian matrix:
where:
It is expressed as follows:
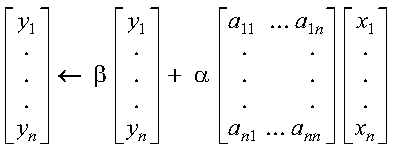
These subroutines compute the matrix-vector product for a real symmetric matrix stored in lower-packed storage mode:
where:
It is expressed as follows:
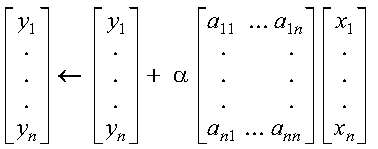
None
This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| 8.0 4.0 2.0 |
| 4.0 6.0 7.0 |
| 2.0 7.0 3.0 |
* *
UPLO N ALPHA AP X INCX BETA Y INCY
| | | | | | | | |
CALL SSPMV( 'L' , 3 , 1.0 , AP , X , 1 , 1.0 , Y , 2 )
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
Y = (39.0, . , 34.0, . , 25.0)
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 1.0. The real symmetric matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA AP X INCX BETA Y INCY
| | | | | | | | |
CALL SSPMV( 'U' , 3 , 1.0 , AP , X , -2 , 2.0 , Y , 1 )
AP = (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)
X = (4.0, . , 2.0, . , 1.0)
Y = (6.0, 5.0, 4.0)
Y = (36.0, 54.0, 36.0)
This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| (1.0, 0.0) (3.0, 5.0) (2.0, -3.0) |
| (3.0, -5.0) (7.0, 0.0) (4.0, -8.0) |
| (2.0, 3.0) (4.0, 8.0) (6.0, 0.0) |
* *
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. |
UPLO N ALPHA AP X INCX BETA Y INCY
| | | | | | | | |
CALL CHPMV( 'L' , 3 , ALPHA , AP , X , 1 , BETA , Y , 2 )
ALPHA = (1.0, 0.0)
AP = ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
(4.0, 8.0), (6.0, . ))
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
BETA = (1.0, 0.0)
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
Y = ((32.0, 21.0), . , (87.0, -8.0), . , (32.0, 64.0))
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. |
UPLO N ALPHA AP X INCX BETA Y INCY
| | | | | | | | |
CALL CHPMV( 'U' , 3 , ALPHA , AP , X , -2 , BETA , Y , 2 )
ALPHA = (1.0, 0.0)
AP = ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
(4.0, -8.0), (6.0, . ))
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
BETA = (0.0, 0.0)
Y =(not relevant)
Y = ((31.0, 21.0), . , (85.0, -7.0), . , (30.0, 63.0))
This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | |
CALL SSYMV( 'L' , 3 , 1.0 , A , 3 , X , 1 , 1.0 , Y , 2 )
* *
| 8.0 . . |
A = | 4.0 6.0 . |
| 2.0 7.0 3.0 |
* *
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
Y = (39.0, . , 34.0, . , 25.0)
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 1.0. The real symmetric matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | |
CALL SSYMV( 'U' , 3 , 1.0 , A , 4 , X , -2 , 2.0 , Y , 1 )
* *
| 8.0 4.0 2.0 |
A = | . 6.0 7.0 |
| . . 3.0 |
| . . . |
* *
X = (4.0, . , 2.0, . , 1.0)
Y = (6.0, 5.0, 4.0)
A = (36.0, 54.0, 36.0)
This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. |
UPLO N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | |
CALL CHEMV( 'L' , 3 , ALPHA , A , 3 , X , 1 , BETA , Y , 2 )
ALPHA = (1.0, 0.0)
* *
| (1.0, . ) . . |
A = | (3.0, -5.0) (7.0, . ) . |
| (2.0, 3.0) (4.0, 8.0) (6.0, . ) |
* *
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
BETA = (1.0, 0.0)
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
Y = ((32.0, 21.0), . , (87.0, -8.0), . , (32.0, 64.0))
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. |
UPLO N ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | |
CALL CHEMV( 'U' , 3 , ALPHA , A , 3 , X , -2 , BETA , Y , 2 )
ALPHA = (1.0, 0.0)
* *
| (1.0, . ) (3.0, 5.0) (2.0, -3.0) |
A = | . (7.0, . ) (4.0, -8.0) |
| . . (6.0, . ) |
* *
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0)) BETA = (0.0, 0.0) Y =(not relevant)
Y = ((31.0, 21.0), . , (85.0, -7.0), . , (30.0, 63.0))
This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3. Matrix A is:
* *
| 8.0 4.0 2.0 |
| 4.0 6.0 7.0 |
| 2.0 7.0 3.0 |
* *
N ALPHA AP X INCX Y INCY
| | | | | | |
CALL SSLMX( 3 , 1.0 , AP , X , 1 , Y , 2 )
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
Y = (39.0, . , 34.0, . , 25.0)
SSPR, DSPR, SSYR, DSYR, SSLR1, and DSLR1 compute the rank-one update of a real symmetric matrix, using the scalar alpha, matrix A, vector x, and its transpose xT:
CHPR, ZHPR, CHER, and ZHER compute the rank-one update of a complex Hermitian matrix, using the scalar alpha, matrix A, vector x, and its conjugate transpose xH:
The following storage modes are used:
| A, x | alpha | Subprogram |
| Short-precision real | Short-precision real | SSPR, SSYR, and SSLR1 |
| Long-precision real | Long-precision real | DSPR, DSYR, and DSLR1 |
| Short-precision complex | Short-precision real | CHPR and CHER |
| Long-precision complex | Long-precision real | ZHPR and ZHER |
| Note: | SSPR and DSPR are Level 2 BLAS subroutines. You should use these subroutines instead of SSLR1 and DSLR1, which are only provided for compatibility with earlier releases of ESSL. |
| Fortran | CALL SSPR | DSPR | CHPR | ZHPR (uplo, n,
alpha, x, incx, ap)
CALL SSYR | DSYR | CHER | ZHER (uplo, n, alpha, x, incx, a, lda) CALL SSLR1 | DSLR1 (n, alpha, x, incx, ap) |
| C and C++ | sspr | dspr | chpr | zhpr (uplo, n, alpha,
x, incx, ap);
ssyr | dsyr | cher | zher (uplo, n, alpha, x, incx, a, lda); sslr1 | dslr1 (n, alpha, x, incx, ap); |
| PL/I | CALL SSPR | DSPR | CHPR | ZHPR (uplo, n,
alpha, x, incx, ap);
CALL SSYR | DSYR | CHER | ZHER (uplo, n, alpha, x, incx, a, lda); CALL SSLR1 | DSLR1 (n, alpha, x, incx, ap); |
If uplo = 'U', A is stored in upper-packed or upper storage mode.
If uplo = 'L', A is stored in lower-packed or lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
For SSPR, DSPR, CHPR, ZHPR, SSYR, DSYR, CHER, and ZHER, incx < 0 or incx > 0.
For SSLR1 and DSLR1, incx can have any value.
For SSPR and DSPR, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.
For CHPR and ZHPR, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.
For SSLR1 and DSLR1, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.
Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 65.
For SSYR and DSYR, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.
For CHER and ZHER, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 65.
These subroutines perform the computations described in the two sections below. See references [34], [35], and [73]. If n or alpha is 0, no computation is performed.
For CHPR and CHER, intermediate results are accumulated in long precision. For SSPR, SSYR, and SSLR1, intermediate results are accumulated in long precision on some platforms.
These subroutines compute the rank-one update of a real symmetric matrix:
where:
It is expressed as follows:
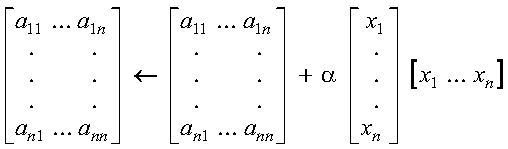
These subroutines compute the rank-one update of a complex Hermitian matrix:
where:
It is expressed as follows:
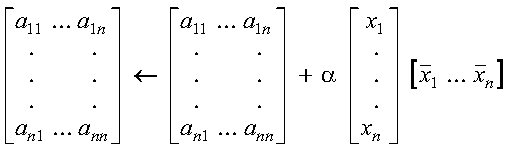
None
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| 8.0 4.0 2.0 |
| 4.0 6.0 7.0 |
| 2.0 7.0 3.0 |
* *
UPLO N ALPHA X INCX AP
| | | | | |
CALL SSPR( 'L' , 3 , 1.0 , X , 1 , AP )
X = (3.0, 2.0, 1.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)
This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX AP
| | | | | |
CALL SSPR( 'U' , 3 , 1.0 , X , -2 , AP )
X = (1.0, . , 2.0, . , 3.0)
AP = (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)
AP = (17.0, 10.0, 10.0, 5.0, 9.0, 4.0)
This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| (1.0, 0.0) (3.0, 5.0) (2.0, -3.0) |
| (3.0, -5.0) (7.0, 0.0) (4.0, -8.0) |
| (2.0, 3.0) (4.0, 8.0) (6.0, 0.0) |
* *
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero. |
UPLO N ALPHA X INCX AP
| | | | | |
CALL CHPR( 'L' , 3 , 1.0 , X , 1 , AP )
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
AP = ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
(4.0, 8.0), (6.0, . ))
AP = ((6.0, 0.0), (7.0, -13.0), (13.0, 1.0), (23.0, 0.0),
(16.0, 24.0), (31.0, 0.0))
This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero. |
UPLO N ALPHA X INCX AP
| | | | | |
CALL CHPR( 'U' , 3 , 1.0 , X , -2 , AP )
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
AP = ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
(4.0, -8.0), (6.0, . ))
AP = ((6.0, 0.0), (7.0, 13.0), (23.0, 0.0), (13.0, -1.0),
(16.0, -24.0), (31.0, 0.0))
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL SSYR( 'L' , 3 , 1.0 , X , 1 , A , 3 )
X = (3.0, 2.0, 1.0)
* *
| 8.0 . . |
A = | 4.0 6.0 . |
| 2.0 7.0 3.0 |
* *
* *
| 17.0 . . |
A = | 10.0 10.0 . |
| 5.0 9.0 4.0 |
* *
This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL SSYR( 'U' , 3 , 1.0 , X , -2 , A , 4 )
X = (1.0, . , 2.0, . , 3.0)
* *
| 8.0 4.0 2.0 |
A = | . 6.0 7.0 |
| . . 3.0 |
| . . . |
* *
* *
| 17.0 10.0 5.0 |
A = | . 10.0 9.0 |
| . . 4.0 |
| . . . |
* *
This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero. |
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL CHER( 'L' , 3 , 1.0 , X , 1 , A , 3 )
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
* *
| (1.0, . ) . . |
A = | (3.0, -5.0) (7.0, . ) . |
| (2.0, 3.0) (4.0, 8.0) (6.0, . ) |
* *
* *
| (6.0, 0.0) . . |
A = | (7.0, -13.0) (23.0, 0.0) . |
| (13.0, 1.0) (16.0, 24.0) (31.0, 0.0) |
* *
This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero. |
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL CHER( 'U' , 3 , 1.0 , X , -2 , A , 3 )
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
* *
| (1.0, . ) (3.0, 5.0) (2.0, -3.0) |
A = | . (7.0, . ) (4.0, -8.0) |
| . . (6.0, . ) |
* *
* *
| (6.0, 0.0) (7.0, 13.0) (13.0, -1.0) |
A = | . (23.0, 0.0) (16.0, -24.0) |
| . . (31.0, 0.0) |
* *
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. It uses the same input matrix A as in Example 1.
N ALPHA X INCX AP
| | | | |
CALL SSLR1( 3 , 1.0 , X , 1 , AP )
X = (3.0, 2.0, 1.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)
SSPR2, DSPR2, SSYR2, DSYR2, SSLR2, and DSLR2 compute the rank-two update of a real symmetric matrix, using the scalar alpha, matrix A, vectors x and y, and their transposes xT and yT:
CHPR2, ZHPR2, CHER2, and ZHER2, compute the rank-two update of a complex Hermitian matrix, using the scalar alpha, matrix A, vectors x and y, and their conjugate transposes xH and yH:
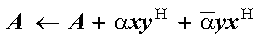
The following storage modes are used:
| alpha, A, x, y | Subprogram |
| Short-precision real | SSPR2, SSYR2, and SSLR2 |
| Long-precision real | DSPR2, DSYR2, and DSLR2 |
| Short-precision complex | CHPR2 and CHER2 |
| Long-precision complex | ZHPR2 and ZHER2 |
| Note: | SSPR2 and DSPR2 are Level 2 BLAS subroutines. You should use these subroutines instead of SSLR2 and DSLR2, which are only provided for compatibility with earlier releases of ESSL. |
| Fortran | CALL SSPR2 | DSPR2 | CHPR2 | ZHPR2 (uplo, n,
alpha, x, incx, y, incy,
ap)
CALL SSYR2 | DSYR2 | CHER2 | ZHER2 (uplo, n, alpha, x, incx, y, incy, a, lda) CALL SSLR2 | DSLR2 (n, alpha, x, incx, y, incy, ap) |
| C and C++ | sspr2 | dspr2 | chpr2 | zhpr2 (uplo, n, alpha,
x, incx, y, incy, ap);
ssyr2 | dsyr2 | cher2 | zher2 (uplo, n, alpha, x, incx, y, incy, a, lda); sslr2 | dslr2 (n, alpha, x, incx, y, incy, ap); |
| PL/I | CALL SSPR2 | DSPR2 | CHPR2 | ZHPR2 (uplo, n,
alpha, x, incx, y, incy,
ap);
CALL SSYR2 | DSYR2 | CHER2 | ZHER2 (uplo, n, alpha, x, incx, y, incy, a lda); CALL SSLR2 | DSLR2 (n, alpha, x, incx, y, incy, ap); |
If uplo = 'U', A is stored in upper-packed or upper storage mode.
If uplo = 'L', A is stored in lower-packed or lower storage mode.
Specified as: a single character. It must be 'U&csq or 'L'.
Specified as: a fullword integer, where:
For SSPR2, DSPR2, CHPR2, ZHPR2, SSYR2, DSYR2, CHER2, and ZHER2, incx < 0 or incx > 0.
For SSLR2 and DSLR2, incx can have any value.
For SSPR2, DSPR2, CHPR2, ZHPR2, SSYR2, DSYR2, CHER2, and ZHER2, incy < 0 or incy > 0.
For SSLR2 and DSLR2, incy can have any value.
For SSPR2 and DSPR2, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.
For CHPR2 and ZHPR2, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.
For SSLR2 and DSLR2, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.
Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 66.
For SSYR2 and DSYR2, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.
For CHER2 and ZHER2, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 66.
These subroutines perform the computation described in the two sections below. See references [34], [35], and [73]. If n or alpha is zero, no computation is performed.
For SSPR2, SSYR2, SSLR2, CHPR2, and CHER2, intermediate results are accumulated in long precision.
These subroutines compute the rank-two update of a real symmetric matrix:
where:
It is expressed as follows:
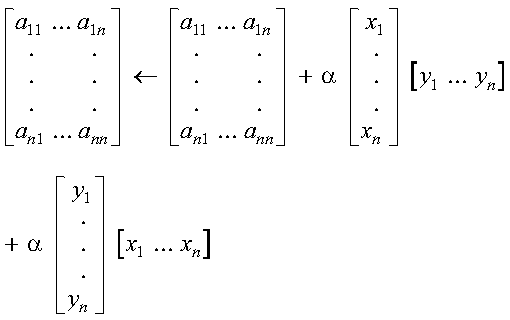
These subroutines compute the rank-two update of a complex Hermitian matrix:
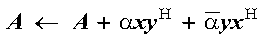
where:
It is expressed as follows:
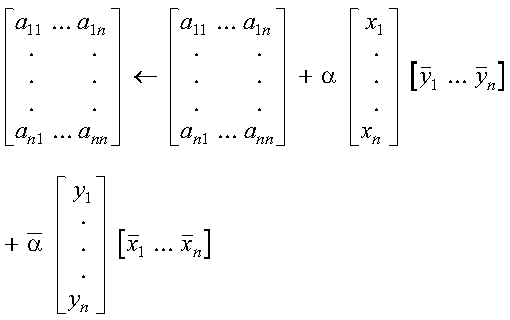
None
This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| 8.0 4.0 2.0 |
| 4.0 6.0 7.0 |
| 2.0 7.0 3.0 |
* *
UPLO N ALPHA X INCX Y INCY AP
| | | | | | | |
CALL SSPR2( 'L' , 3 , 1.0 , X , 1 , Y , 2 , AP )
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (38.0, 23.0, 13.0, 18.0, 14.0, 7.0)
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 3.0. The real symmetric matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX Y INCY AP
| | | | | | | |
CALL SSPR2( 'U' , 3 , 1.0 , X , -2 , Y , 2 , AP )
X = (1.0, . , 2.0, . , 3.0)
Y = (5.0, . , 3.0, . , 2.0)
AP = (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)
AP = (38.0, 23.0, 18.0, 13.0, 14.0, 7.0)
This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| (1.0, 0.0) (3.0, 5.0) (2.0, -3.0) |
| (3.0, -5.0) (7.0, 0.0) (4.0, -8.0) |
| (2.0, 3.0) (4.0, 8.0) (6.0, 0.0) |
* *
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> zero, the imaginary parts of the diagonal elements are set to zero. |
UPLO N ALPHA X INCX Y INCY AP
| | | | | | | |
CALL CHPR2( 'L' , 3 , ALPHA , X , 1 , Y , 2 , AP )
ALPHA = (1.0, 0.0)
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
AP = ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
(4.0, 8.0), (6.0, . ))
AP = ((3.0, 0.0), (7.0, -10.0), (9.0, 4.0), (23.0, 0.0),
(14.0, 23.0), (26.0, 0.0))
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0,2.0). The complex Hermitian matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> zero, the imaginary parts of the diagonal elements are set to zero. |
UPLO N ALPHA X INCX Y INCY AP
| | | | | | | |
CALL CHPR2( 'U' , 3 , ALPHA , X , -2 , Y , 2 , AP )
ALPHA = (1.0, 0.0)
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
AP = ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
(4.0, -8.0), (6.0, . ))
AP = ((3.0, 0.0), (7.0, 10.0), (23.0, 0.0), (9.0, -4.0),
(14.0, -23.0), (26.0, 0.0))
This example shows vectors x and y with positive strides, and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SSYR2( 'L' , 3 , 1.0 , X , 1 , Y , 2 , A , 3 )
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
* *
| 8.0 . . |
A = | 4.0 6.0 . |
| 2.0 7.0 3.0 |
* *
* *
| 38.0 . . |
A = | 23.0 18.0 . |
| 13.0 14.0 7.0 |
* *
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 3.0. The real symmetric matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL SSYR2( 'U' , 3 , 1.0 , X , -2 , Y , 2 , A , 4 )
X = (1.0, . , 2.0, . , 3.0)
Y = (5.0, . , 3.0, . , 2.0)
* *
| 8.0 4.0 2.0 |
A = | . 6.0 7.0 |
| . . 3.0 |
| . . . |
* *
* *
| 38.0 23.0 13.0 |
A = | . 18.0 14.0 |
| . . 7.0 |
| . . . |
* *
This example shows vector x and y with positive stride, and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> zero, the imaginary parts of the diagonal elements are set to zero. |
UPLO N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL CHER2( 'L' , 3 , ALPHA , X , 1 , Y , 2 , A , 3 )
ALPHA = (1.0, 0.0)
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
* *
| (1.0, . ) . . |
A = | (3.0, -5.0) (7.0, . ) . |
| (2.0, 3.0) (4.0, 8.0) (6.0, . ) |
* *
* *
| (3.0, 0.0) . . |
A = | (7.0, -10.0) (23.0, 0.0 ) . |
| (9.0, 4.0) (14.0, 23.0) (26.0, 0.0 ) |
* *
This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 3.
| Note: | On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> zero, the imaginary parts of the diagonal elements are set to zero. |
UPLO N ALPHA X INCX Y INCY A LDA
| | | | | | | | |
CALL CHER2( 'U' , 3 , ALPHA , X , -2 , Y , 2 , A , 3 )
ALPHA = (1.0, 0.0)
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
Y = ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
* *
| (1.0, . ) (3.0, 5.0) (2.0, -3.0) |
A = | . (7.0, . ) (4.0, -8.0) |
| . . (6.0, . ) |
* *
* *
| (3.0, 0.0) (7.0, 10.0) (9.0, -4.0) |
A = | . (23.0, 0.0) (14.0, -23.0) |
| . . (26.0, 0.0) |
* *
This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. It uses the same input matrix A as in Example 1.
N ALPHA X INCX Y INCY AP
| | | | | | |
CALL SSLR2( 3 , 1.0 , X , 1 , Y , 2 , AP )
X = (3.0, 2.0, 1.0)
Y = (5.0, . , 3.0, . , 2.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (38.0, 23.0, 13.0, 18.0, 14.0, 7.0)
SGBMV and DGBMV compute the matrix-vector product for either a real general band matrix or its transpose, where the general band matrix is stored in BLAS-general-band storage mode. It uses the scalars alpha and beta, vectors x and y, and general band matrix A or its transpose:
CGBMV and ZGBMV compute the matrix-vector product for either a complex general band matrix, its transpose, or its conjugate transpose, where the general band matrix is stored in BLAS-general-band storage mode. It uses the scalars alpha and beta, vectors x and y, and general band matrix A, its transpose, or its conjugate transpose:
| alpha, beta, x, y, A | Subprogram |
| Short-precision real | SGBMV |
| Long-precision real | DGBMV |
| Short-precision complex | CGBMV |
| Long-precision complex | ZGBMV |
| Fortran | CALL SGBMV | DGBMV | CGBMV | ZGBMV (transa, m, n, ml, mu, alpha, a, lda, x, incx, beta, y, incy) |
| C and C++ | sgbmv | dgbmv | cgbmv | zgbmv (transa, m, n, ml, mu, alpha, a, lda, x, incx, beta, y, incy); |
| PL/I | CALL SGBMV | DGBMV | CGBMV | ZGBMV (transa, m, n, ml, mu, alpha, a, lda, x, incx, beta, y, incy); |
If transa = 'N', A is used in the computation.
If transa = 'T', AT is used in the computation.
If transa = 'C', AH is used in the computation.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If transa = 'N', it is the length of vector y.
If transa = 'T' or 'C', it is the length of vector x.
Specified as: a fullword integer; m >= 0.
If transa = 'N', it is the length of vector x.
If transa = 'T' or 'C', it is the length of vector y.
Specified as: a fullword integer; n >= 0.
If transa = 'N', A is used in the computation.
If transa = 'T', AT is used in the computation.
If transa = 'C', AH is used in the computation.
| Note: | No data should be moved to form AT or AH; that is, the matrix A should always be stored in its untransposed form in BLAS-general-band storage mode. |
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 67, where lda >= ml+mu+1.
If transa = 'N', it has length n.
If transa = 'T' or 'C', it has length m.
Specified as: a one-dimensional array, containing numbers of the data type indicated in Table 67, where:
If transa = 'N', it must have at least 1+(n-1)|incx| elements.
If transa = 'T' or 'C', it must have at least 1+(m-1)|incx| elements.
If transa = 'N', it has length m.
If transa = 'T' or 'C', it has length n.
Specified as: a one-dimensional array, containing numbers of the data type indicated in Table 67, where:
If transa = 'N', it must have at least 1+(m-1)|incy| elements.
If transa = 'T' or 'C', it must have at least 1+(n-1)|incy| elements.
If transa = 'N', it has length m.
If transa = 'T' or 'C', it has length n.
Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 67.
The possible computations that can be performed by these subroutines are described in the following sections. Varying implementation techniques are used for this computation to improve performance. As a result, accuracy of the computational result may vary for different computations.
In all the computations, general band matrix A is stored in its untransposed form in an array, using BLAS-general-band storage mode.
For SGBMV and CGBMV, intermediate results are accumulated in long precision. Occasionally, for performance reasons, these intermediate results are truncated to short precision and stored.
See references [34], [35], [38], [46], and [73]. No computation is performed if m or n is 0 or if alpha is zero and beta is one.
For SGBMV, DGBMV, CGBMV, and ZGBMV, the matrix-vector product for a general band matrix is expressed as follows:
where:
For SGBMV, DGBMV, CGBMV, and ZGBMV, the matrix-vector product for the transpose of a general band matrix is expressed as:
where:
For CGBMV and ZGBMV, the matrix-vector product for the conjugate transpose of a general band matrix is expressed as follows:
where:
None
This example shows how to use DGBMV to perform the computation y <-- betay+alphaAx, where TRANSA is equal to 'N', and the following real general band matrix A is used in the computation. Matrix A is:
* *
| 1.0 1.0 1.0 0.0 |
| 2.0 2.0 2.0 2.0 |
| 3.0 3.0 3.0 3.0 |
| 4.0 4.0 4.0 4.0 |
| 0.0 5.0 5.0 5.0 |
* *
TRANSA M N ML MU ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | | | |
CALL SGBMV( 'N' , 5 , 4 , 3 , 2 , 2.0 , A , 8 , X , 1 , 10.0 , Y , 2 )
* *
| . . 1.0 2.0 |
| . 1.0 2.0 3.0 |
| 1.0 2.0 3.0 4.0 |
A = | 2.0 3.0 4.0 5.0 |
| 3.0 4.0 5.0 . |
| 4.0 5.0 . . |
| . . . . |
| . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0) Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0, . )
Y = (22.0, . , 60.0, . , 90.0, . , 120.0, . , 140.0, . )
This example shows how to use SGBMV to perform the computation y <-- betay+alphaATx, where TRANSA is equal to 'T', and the transpose of a real general band matrix A is used in the computation. It uses the same input as Example 1.
TRANSA M N ML MU ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | | | |
CALL SGBMV( 'T' , 5 , 4 , 3 , 2 , 2.0 , A , 8 , X , 1 , 10.0 , Y , 2 )
Y = (70.0, . , 130.0, . , 140.0, . , 148.0, . )
This example shows how to use CGBMV to perform the computation y <-- betay+alphaAHx, where TRANSA is equal to 'C', and the complex conjugate of the following general band matrix A is used in the computation. Matrix A is:
* *
| (1.0, 1.0) (1.0, 1.0) (1.0, 1.0) (0.0, 0.0) |
| (2.0, 2.0) (2.0, 2.0) (2.0, 2.0) (2.0, 2.0) |
| (3.0, 3.0) (3.0, 3.0) (3.0, 3.0) (3.0, 3.0) |
| (4.0, 4.0) (4.0, 4.0) (4.0, 4.0) (4.0, 4.0) |
| (0.0, 0.0) (5.0, 5.0) (5.0, 5.0) (0.0, 0.0) |
* *
TRANSA M N ML MU ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | | | |
CALL CGBMV( 'C' , 5 , 4 , 3 , 2 , ALPHA , A , 8 , X , 1 , BETA , Y , 2 )
* *
| . . (1.0, 1.0) (2.0, 2.0) |
| . (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) |
| (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) |
A = | (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) |
| (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) . |
| (4.0, 4.0) (5.0, 5.0) . . |
| . . . . |
| . . . . |
* *
X = ((1.0, 2.0), (2.0, 3.0), (3.0, 4.0), (4.0, 5.0),
(5.0, 6.0))
ALPHA = (1.0, 1.0)
BETA = (10.0, 0.0)
Y = ((1.0, 2.0), . , (2.0, 3.0), . , (3.0, 4.0), . ,
(4.0, 5.0), . )
Y = ((70.0, 100.0), . , (130.0, 170.0), . ,
(140.0, 180.0), . , (148.0, 186.0), . )
This example shows how to use SGBMV to perform the computation y <-- betay+alphaAx, where ml >= m and mu >= n, TRANSA is equal to 'N', and the following real general band matrix A is used in the computation. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 1.0 |
| 2.0 2.0 2.0 2.0 2.0 |
| 3.0 3.0 3.0 3.0 3.0 |
| 4.0 4.0 4.0 4.0 4.0 |
* *
TRANSA M N ML MU ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | | | |
CALL SGBMV( 'N' , 4 , 5 , 6 , 5 , 2.0 , A , 12 , X , 1 , 10.0 , Y , 2 )
* *
| . . . . . |
| . . . . 1.0 |
| . . . 1.0 2.0 |
| . . 1.0 2.0 3.0 |
| . 1.0 2.0 3.0 4.0 |
A = | 1.0 2.0 3.0 4.0 . |
| 2.0 3.0 4.0 . . |
| 3.0 4.0 . . . |
| 4.0 . . . . |
| . . . . . |
| . . . . . |
| . . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . )
Y = (40.0, . , 80.0, . , 120.0, . , 160.0, . )
SSBMV and DSBMV compute the matrix-vector product for a real symmetric band matrix. CHBMV and ZHBMV compute the matrix-vector product for a complex Hermitian band matrix. The band matrix A is stored in either upper- or lower-band-packed storage mode. It uses the scalars alpha and beta, vectors x and y, and band matrix A:
| alpha, beta, x, y, A | Subprogram |
| Short-precision real | SSBMV |
| Long-precision real | DSBMV |
| Short-precision complex | CHBMV |
| Long-precision complex | ZHBMV |
| Fortran | CALL SSBMV | DSBMV | CHBMV | ZHBMV (uplo, n, k, alpha, a, lda, x, incx, beta, y, incy) |
| C and C++ | ssbmv | dsbmv | chbmv | zhbmv (uplo, n, k, alpha, a, lda, x, incx, beta, y, incy); |
| PL/I | CALL SSBMV | DSBMV | CHBMV | ZHBMV (uplo, n, k, alpha, a, lda, x, incx, beta, y, incy); |
If uplo = 'U', A is stored in upper-band-packed storage mode.
If uplo = 'L', A is stored in lower-band-packed storage mode.
Specified as: a single character. It must be 'U' or 'L'.
If uplo = 'U', A is stored in upper-band-packed storage mode.
If uplo = 'L', A is stored in lower-band-packed storage mode.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 68, where lda >= k+1.
These subroutines perform the following matrix-vector product, using a real symmetric or complex Hermitian band matrix A, stored in either upper- or lower-band-packed storage mode:
where:
For SSBMV and CHBMV, intermediate results are accumulated in long precision. Occasionally, for performance reasons, these intermediate results are truncated to short precision and stored.
See references [34], [38], [46], and [73]. No computation is performed if n is 0 or if alpha is zero and beta is one.
None
This example shows how to use SSBMV to perform the matrix-vector product, where the real symmetric band matrix A of order 7 and half band width of 3 is stored in upper-band-packed storage mode. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 1.0 2.0 2.0 2.0 2.0 0.0 0.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 0.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 |
| 0.0 2.0 3.0 4.0 5.0 5.0 5.0 |
| 0.0 0.0 3.0 4.0 5.0 6.0 6.0 |
| 0.0 0.0 0.0 4.0 5.0 6.0 7.0 |
* *
UPLO N K ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL SSBMV( 'U' , 7 , 3 , 2.0 , A , 5 , X , 1 , 10.0 , Y , 2 )
* *
| . . . 1.0 2.0 3.0 4.0 |
| . . 1.0 2.0 3.0 4.0 5.0 |
A = | . 1.0 2.0 3.0 4.0 5.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 |
| . . . . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0)
Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0, . , 6.0, . , 7.0)
Y = (30.0, . , 78.0, . , 148.0, . , 244.0, . , 288.0, . ,
316.0, . , 322.0)
This example shows how to use CHBMV to perform the matrix-vector product, where the complex Hermitian band matrix A of order 7 and half band width of 3 is stored in lower-band-packed storage mode. Matrix A is:
* *
| (1.0, 0.0) (1.0, 1.0) (1.0, 1.0) (1.0, 1.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, -1.0) (2.0, 0.0) (2.0, 2.0) (2.0, 2.0) (2.0, 2.0) (0.0, 0.0) (0.0, 0.0) |
| (1.0, -1.0) (2.0, -2.0) (3.0, 0.0) (3.0, 3.0) (3.0, 3.0) (3.0, 3.0) (0.0, 0.0) |
| (1.0, -1.0) (2.0, -2.0) (3.0, -3.0) (4.0, 0.0) (4.0, 4.0) (4.0, 4.0) (4.0, 4.0) |
| (0.0, 0.0) (2.0, -2.0) (3.0, -3.0) (4.0, -4.0) (5.0, 0.0) (5.0, 5.0) (5.0, 5.0) |
| (0.0, 0.0) (0.0, 0.0) (3.0, -3.0) (4.0, -4.0) (5.0, -5.0) (6.0, 0.0) (6.0, 6.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (4.0, -4.0) (5.0, -5.0) (6.0, -6.0) (7.0, 0.0) |
* *
| Note: | The imaginary parts of the diagonal elements of a complex Hermitian matrix are assumed to be zero, so you do not need to set these values. |
UPLO N K ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL CHBMV( 'L' , 7 , 3 , ALPHA , A , 5 , X , 1 , BETA , Y , 2 )
ALPHA = (2.0, 0.0)
BETA = (10.0, 0.0)
* *
| (1.0, . ) (2.0, . ) (3.0, . ) (4.0, . ) (5.0, . ) (6.0, . ) (7.0, . ) |
| (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) (6.0, 6.0) . |
A = | (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) . . |
| (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) . . . |
| . . . . . . . |
* *
X = ((1.0, 1.0), (2.0, 2.0), (3.0, 3.0), (4.0, 4.0),
(5.0, 5.0), (6.0, 6.0), (7.0, 7.0))
Y = ((1.0, 1.0), . , (2.0, 2.0), . , (3.0, 3.0), . ,
(4.0, 4.0), . , (5.0, 5.0), . , (6.0, 6.0), . ,
(7.0, 7.0))
Y = ((48.0, 12.0), . , (124.0, 32.0), . , (228.0, 68.0), . ,
(360.0, 128.0), . , (360.0, 216.0), . ,
(300.0, 332.0), . , (168.0, 476.0))
This example shows how to use SSBMV to perform the matrix-vector product, where n >= k. Matrix A is a real 5 by 5 symmetric band matrix with a half band width of 5, stored in upper-band-packed storage mode. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 1.0 |
| 1.0 2.0 2.0 2.0 2.0 |
| 1.0 2.0 3.0 3.0 3.0 |
| 1.0 2.0 3.0 4.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 |
* *
UPLO N K ALPHA A LDA X INCX BETA Y INCY
| | | | | | | | | | |
CALL SSBMV( 'U' , 5 , 5 , 2.0 , A , 7 , X , 1 , 10.0 , Y , 2 )
* *
| . . . . . |
| . . . . 1.0 |
| . . . 1.0 2.0 |
A = | . . 1.0 2.0 3.0 |
| . 1.0 2.0 3.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 |
| . . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0, . )
Y = (40.0, . , 78.0, . , 112.0, . , 140.0, . , 160.0, . )
STRMV, DTRMV, STPMV, and DTPMV compute one of the following matrix-vector products, using the vector x and triangular matrix A or its transpose:
CTRMV, ZTRMV, CTPMV, and ZTPMV compute one of the following matrix-vector products, using the vector x and triangular matrix A, its transpose, or its conjugate transpose:
Matrix A can be either upper or lower triangular, where:
| A, x | Subprogram |
| Short-precision real | STRMV and STPMV |
| Long-precision real | DTRMV and DTPMV |
| Short-precision complex | CTRMV and CTPMV |
| Long-precision complex | ZTRMV and ZTPMV |
| Fortran | CALL STRMV | DTRMV | CTRMV | ZTRMV (uplo, transa,
diag, n, a, lda, x,
incx)
CALL STPMV | DTPMV | CTPMV | ZTPMV (uplo, transa, diag, n, ap, x, incx) |
| C and C++ | strmv | dtrmv | ctrmv | ztrmv (uplo, transa,
diag, n, a, lda, x,
incx);
stpmv | dtpmv | ctpmv | ztpmv (uplo, transa, diag, n, ap, x, incx); |
| PL/I | CALL STRMV | DTRMV | CTRMV | ZTRMV (uplo, transa,
diag, n, a, lda, x,
incx);
CALL STPMV | DTPMV | CTPMV | ZTPMV (uplo, transa, diag, n, ap, x, incx); |
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If transa = 'N', A is used in the computation.
If transa = 'T', AT is used in the computation.
If transa = 'C', AH is used in the computation.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
| Note: | No data should be moved to form AT or AH; that is, the matrix A should always be stored in its untransposed form. |
These subroutines can perform the following matrix-vector product computations, using the triangular matrix A, its transpose, or its conjugate transpose, where A can be either upper or lower triangular:
where:
See references [32] and [38]. If n is 0, no computation is performed.
None
This example shows the computation x <-- Ax. Matrix A is a real 4 by 4 lower triangular matrix that is unit triangular, stored in lower-triangular storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 . . . |
| 1.0 1.0 . . |
| 2.0 3.0 1.0 . |
| 3.0 4.0 3.0 1.0 |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL STRMV( 'L' , 'N' , 'U' , 4 , A , 4 , X , 1 )
* *
| . . . . |
A = | 1.0 . . . |
| 2.0 3.0 . . |
| 3.0 4.0 3.0 . |
* *
X = (1.0, 2.0, 3.0, 4.0)
X = (1.0, 3.0, 11.0, 24.0)
This example shows the computation x <-- ATx. Matrix A is a real 4 by 4 upper triangular matrix that is unit triangular, stored in upper-triangular storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 2.0 3.0 2.0 |
| . 1.0 2.0 5.0 |
| . . 1.0 3.0 |
| . . . 1.0 |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL STRMV( 'U' , 'T' , 'U' , 4 , A , 4 , X , 1 )
* *
| . 2.0 3.0 2.0 |
A = | . . 2.0 5.0 |
| . . . 3.0 |
| . . . . |
* *
X = (5.0, 4.0, 3.0, 2.0)
X = (5.0, 14.0, 26.0, 41.0)
This example shows the computation x <-- AHx. Matrix A is a complex 4 by 4 upper triangular matrix that is unit triangular, stored in upper-triangular storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| (1.0, 0.0) (2.0, 2.0) (3.0, 3.0) (2.0, 2.0) |
| . (1.0, 0.0) (2.0, 2.0) (5.0, 5.0) |
| . . (1.0, 0.0) (3.0, 3.0) |
| . . . (1.0, 0.0) |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of (1.0, 0.0) for the diagonal elements. |
UPLO TRANSA DIAG N A LDA X INCX
| | | | | | | |
CALL CTRMV( 'U' , 'C' , 'U' , 4 , A , 4 , X , 1 )
* *
| . (2.0, 2.0) (3.0, 3.0) (2.0, 2.0) |
A = | . . (2.0, 2.0) (5.0, 5.0) |
| . . . (3.0, 3.0) |
| . . . . |
* *
X = ((5.0, 5.0), (4.0, 4.0), (3.0, 3.0), (2.0, 2.0))
X = ((5.0, 5.0), (24.0, 4.0), (49.0, 3.0), (80.0, 2.0))
This example shows the computation x <-- Ax. Matrix A is a real 4 by 4 lower triangular matrix that is unit triangular, stored in lower-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 . . . |
| 1.0 1.0 . . |
| 2.0 3.0 1.0 . |
| 3.0 4.0 3.0 1.0 |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of 1.0 for the diagonal elements. |
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL STPMV( 'L' , 'N' , 'U' , 4 , AP , X , 1 )
AP = ( . , 1.0, 2.0, 3.0, . , 3.0, 4.0, . , 3.0, . )
X = (1.0, 2.0, 3.0, 4.0)
X = (1.0, 3.0, 11.0, 24.0)
This example shows the computation x <-- ATx. Matrix A is a real 4 by 4 upper triangular matrix that is not unit triangular, stored in upper-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 2.0 3.0 2.0 |
| . 2.0 2.0 5.0 |
| . . 3.0 3.0 |
| . . . 1.0 |
* *
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL STPMV( 'U' , 'T' , 'N' , 4 , AP , X , 1 )
AP = (1.0, 2.0, 2.0, 3.0, 2.0, 3.0, 2.0, 5.0, 3.0, 1.0)
X = (5.0, 4.0, 3.0, 2.0)
X = (5.0, 18.0, 32.0, 41.0)
This example shows the computation x <-- AHx. Matrix A is a complex 4 by 4 upper triangular matrix that is unit triangular, stored in upper-triangular-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| (1.0, 0.0) (2.0, 2.0) (3.0, 3.0) (2.0, 2.0) |
| . (1.0, 0.0) (2.0, 2.0) (5.0, 5.0) |
| . . (1.0, 0.0) (3.0, 3.0) |
| . . . (1.0, 0.0) |
* *
| Note: | Because matrix A is unit triangular, the diagonal elements are not referenced. ESSL assumes a value of (1.0, 0.0) for the diagonal elements. |
UPLO TRANSA DIAG N AP X INCX
| | | | | | |
CALL CTPMV( 'U' , 'C' , 'U' , 4 , AP , X , 1 )
AP = ( . , (2.0, 2.0), . , (3.0, 3.0), (2.0, 2.0), . ,
(2.0, 2.0), (5.0, 5.0), (3.0, 3.0), . )
X = ((5.0, 5.0), (4.0, 4.0), (3.0, 3.0), (2.0, 2.0))
X = ((5.0, 5.0), (24.0, 4.0), (49.0, 3.0), (80.0, 2.0))
STBMV and DTBMV compute one of the following matrix-vector products, using the vector x and triangular band matrix A or its transpose:
CTBMV and ZTBMV compute one of the following matrix-vector products, using the vector x and triangular band matrix A, its transpose, or its conjugate transpose:
Matrix A can be either upper or lower triangular and is stored
in upper- or lower-triangular-band-packed storage mode, respectively.
| A, x | Subprogram |
| Short-precision real | STBMV |
| Long-precision real | DTBMV |
| Short-precision complex | CTBMV |
| Long-precision complex | ZTBMV |
| Fortran | CALL STBMV | DTBMV | CTBMV | ZTBMV (uplo, transa, diag, n, k, a, lda, x, incx) |
| C and C++ | stbmv | dtbmv | ctbmv | ztbmv (uplo, transa, diag, n, k, a, lda, x, incx); |
| PL/I | CALL STBMV | DTBMV | CTBMV | ZTBMV (uplo, transa, diag, n, k, a, lda, x, incx); |
If uplo = 'U', A is an upper triangular matrix.
If uplo = 'L', A is a lower triangular matrix.
Specified as: a single character. It must be 'U' or 'L'.
If transa = 'N', A is used in the computation.
If transa = 'T', AT is used in the computation.
If transa = 'C', AH is used in the computation.
Specified as: a single character. It must be 'N', 'T', or 'C'.
If diag = 'U', A is a unit triangular matrix.
If diag = 'N', A is not a unit triangular matrix.
Specified as: a single character. It must be 'U' or 'N'.
| Note: | No data should be moved to form AT or AH; that is, the matrix A should always be stored in its untransposed form. |
These subroutines can perform the following matrix-vector product computations, using the triangular band matrix A, its transpose, or its conjugate transpose, where A can be either upper or lower triangular:
where:
See references [34], [46], and [38]. If n is 0, no computation is performed.
None
This example shows the computation x <-- Ax. Matrix A is a real 7 by 7 upper triangular band matrix with a half band width of 3 that is not unit triangular, stored in upper-triangular-band-packed storage mode. Vector x is a vector of length 7. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 0.0 0.0 0.0 |
| 0.0 2.0 2.0 2.0 2.0 0.0 0.0 |
| 0.0 0.0 3.0 3.0 3.0 3.0 0.0 |
| 0.0 0.0 0.0 4.0 4.0 4.0 4.0 |
| 0.0 0.0 0.0 0.0 5.0 5.0 5.0 |
| 0.0 0.0 0.0 0.0 0.0 6.0 6.0 |
| 0.0 0.0 0.0 0.0 0.0 0.0 7.0 |
* *
UPLO TRANSA DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBMV( 'U' , 'N' , 'N' , 7 , 3 , A , 5 , X , 1 )
* *
| . . . 1.0 2.0 3.0 4.0 |
| . . 1.0 2.0 3.0 4.0 5.0 |
A = | . 1.0 2.0 3.0 4.0 5.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 |
| . . . . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0)
X = (10.0, 28.0, 54.0, 88.0, 90.0, 78.0, 49.0)
This example shows the computation x <-- ATx. Matrix A is a real 7 by 7 lower triangular band matrix with a half band width of 3 that is not unit triangular, stored in lower-triangular-band-packed storage mode. Vector x is a vector of length 7. Matrix A is:
* *
| 1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 0.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 3.0 0.0 0.0 0.0 0.0 |
| 1.0 2.0 3.0 4.0 0.0 0.0 0.0 |
| 0.0 2.0 3.0 4.0 5.0 0.0 0.0 |
| 0.0 0.0 3.0 4.0 5.0 6.0 0.0 |
| 0.0 0.0 0.0 4.0 5.0 6.0 7.0 |
* *
UPLO TRANSA DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBMV( 'L' , 'T' , 'N' , 7 , 3 , A , 5 , X , 1 )
* *
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 . |
A = | 1.0 2.0 3.0 4.0 5.0 . . |
| 1.0 2.0 3.0 4.0 . . . |
| . . . . . . . |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0)
X = (10.0, 28.0, 54.0, 88.0, 90.0, 78.0, 49.0)
This example shows the computation x <-- AHx. Matrix A is a complex 7 by 7 upper triangular band matrix with a half band width of 3 that is not unit triangular, stored in upper-triangular-band-packed storage mode. Vector x is a vector of length 7. Matrix A is:
* *
| (1.0, 1.0) (1.0, 1.0) (1.0, 1.0) (1.0, 1.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) |
| (0.0, 0.0) (2.0, 2.0) (2.0, 2.0) (2.0, 2.0) (2.0, 2.0) (0.0, 0.0) (0.0, 0.0) |
| (0.0, 0.0) (0.0, 0.0) (3.0, 3.0) (3.0, 3.0) (3.0, 3.0) (3.0, 3.0) (0.0, 0.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (4.0, 4.0) (4.0, 4.0) (4.0, 4.0) (4.0, 4.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (5.0, 5.0) (5.0, 5.0) (5.0, 5.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (6.0, 6.0) (6.0, 6.0) |
| (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (7.0, 7.0) |
* *
UPLO TRANSA DIAG N K A LDA X INCX
| | | | | | | | |
CALL CTBMV( 'U' , 'C' , 'N' , 7 , 3 , A , 5 , X , 1 )
* *
| . . . (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) |
| . . (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) |
A = | . (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) (6.0, 6.0) |
| (1.0, 1.0) (2.0, 2.0) (3.0, 3.0) (4.0, 4.0) (5.0, 5.0) (6.0, 6.0) (7.0, 7.0) |
| . . . . . . . |
* *
X = ((1.0, 2.0), (2.0, 4.0), (3.0, 6.0), (4.0, 8.0),
(5.0, 10.0), (6.0, 12.0), (7.0, 14.0))
X = ((1.0, 2.0), (7.0, 9.0), (24.0, 23.0), (58.0, 46.0),
(112.0, 79.0), (186.0, 122.0), (280.0, 175.0))
This example shows the computation x <-- ATx, where k > n. Matrix A is a real 4 by 4 upper triangular band matrix with a half band width of 5 that is not unit triangular, stored in upper-triangular-band-packed storage mode. Vector x is a vector of length 4. Matrix A is:
* *
| 1.0 1.0 1.0 1.0 |
| . 2.0 2.0 2.0 |
| . . 3.0 3.0 |
| . . . 4.0 |
* *
UPLO TRANSA DIAG N K A LDA X INCX
| | | | | | | | |
CALL STBMV( 'U' , 'T' , 'N' , 4 , 5 , A , 6 , X , 1 )
* *
| . . . . |
A = | . . . . |
| . . . 1.0 |
| . . 1.0 2.0 |
| . 1.0 2.0 3.0 |
| 1.0 2.0 3.0 4.0 |
* *
X = (1.0, 2.0, 3.0, 4.0)
X = (1.0, 5.0, 14.0, 30.0)
This section contains the sparse matrix-vector subprogram descriptions.
This subprogram computes the matrix-vector product for sparse matrix A, stored in compressed-matrix storage mode, using the matrix and vectors x and y:
where A, x, and y contain long-precision real numbers. You can use DSMTM to transpose matrix A before calling this subroutine. The resulting computation performed by this subroutine is then y <-- ATx.
| Fortran | CALL DSMMX (m, nz, ac, ka, lda, x, y) |
| C and C++ | dsmmx (m, nz, ac, ka, lda, x, y); |
| PL/I | CALL DSMMX (m, nz, ac, ka, lda, x, y); |
The matrix-vector product is computed for a sparse matrix, stored in compressed matrix mode:
where:
It is expressed as follows:
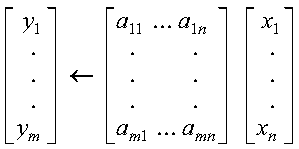
See reference [67]. If m is 0, no computation is performed; if nz is 0, output vector y is set to zero, because matrix A contains all zeros.
If your program uses a sparse matrix stored by rows and you want to use this subroutine, you should first convert your sparse matrix to compressed-matrix storage mode by using the DSRSM utility subroutine described in DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode.
None
This example shows the matrix-vector product computed for the following sparse matrix A, which is stored in compressed-matrix storage mode in arrays AC and KA. Matrix A is:
* *
| 4.0 0.0 7.0 0.0 0.0 0.0 |
| 3.0 4.0 0.0 2.0 0.0 0.0 |
| 0.0 2.0 4.0 0.0 4.0 0.0 |
| 0.0 0.0 7.0 4.0 0.0 1.0 |
| 1.0 0.0 0.0 3.0 4.0 0.0 |
| 1.0 1.0 0.0 0.0 3.0 4.0 |
* *
M NZ AC KA LDA X Y
| | | | | | |
CALL DSMMX( 6 , 4 , AC , KA , 6 , X , Y )
* *
| 4.0 7.0 0.0 0.0 |
| 4.0 3.0 2.0 0.0 |
AC = | 4.0 2.0 4.0 0.0 |
| 4.0 7.0 1.0 0.0 |
| 4.0 1.0 3.0 0.0 |
| 4.0 1.0 1.0 3.0 |
* *
* *
| 1 3 1 1 |
| 2 1 4 1 |
KA = | 3 2 5 1 |
| 4 3 6 1 |
| 5 1 4 1 |
| 6 1 2 5 |
* *
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)
Y = (25.0, 19.0, 36.0, 43.0, 33.0, 42.0)
This subprogram transposes sparse matrix A, stored in compressed-matrix storage mode, where A contains long-precision real numbers.
| Fortran | CALL DSMTM (m, nz, ac, ka, lda, n, nt, at, kt, ldt, aux, naux) |
| C and C++ | dsmtm (m, nz, ac, ka, lda, n, nt, at, kt, ldt, aux, naux); |
| PL/I | CALL DSMTM (m, nz, ac, ka, lda, n, nt, at, kt, ldt, aux, naux); |
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is a storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing long-precision real numbers. They can have any value.
If naux = 0 and error 2015 is unrecoverable, DSMTM dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux >= n.
A sparse matrix A, stored in arrays AC and KA in compressed-matrix storage mode, is transposed, forming AT, and is stored in arrays AT and KT in compressed-matrix storage mode. See reference [67]. This subroutine is provided for when you want to do a matrix-vector product using a transposed matrix, AT. First, you transpose a matrix, A, using this subroutine, then you call DSMMX with the transposed matrix AT. This results in the following computation being performed: y <-- ATx.
If your program uses a sparse matrix stored by rows and you want to use this subroutine, you should first convert your sparse matrix to compressed-matrix storage mode by using the DSRSM utility subroutine described in DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode.
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
None
This example shows how to transpose the following 5 by 4 sparse matrix A, which is stored in compressed-matrix storage mode in arrays AC and KA. Matrix A is:
* *
| 11.0 0.0 0.0 0.0 |
| 21.0 0.0 23.0 0.0 |
| 0.0 0.0 33.0 34.0 |
| 0.0 42.0 0.0 44.0 |
| 51.0 0.0 53.0 0.0 |
* *
The resulting 4 by 5 matrix transpose AT, stored in compressed-matrix storage mode in arrays AT and KT, is as follows. Matrix AT is:
* *
| 11.0 21.0 0.0 0.0 51.0 |
| 0.0 0.0 0.0 42.0 0.0 |
| 0.0 23.0 33.0 0.0 53.0 |
| 0.0 0.0 34.0 44.0 0.0 |
* *
As shown here, the value of N is larger than the actual number of columns in the matrix A. On output, the exact number of rows in the transposed matrix is returned in the output argument N.
On output, row 6 of AT and KT is is not accessed or modified by the subroutine. Column 4 and row 5 are accessed and modified. They are of no use in further computations and will not be used, because NT = 3 and M = 4.
M NZ AC KA LDA N NT AT KT LDT AUX NAUX
| | | | | | | | | | | |
CALL DSMTM( 5 , 2 , AC , KA , 5 , 5 , 4 , AT , KT , 6 , AUX , 5 )
* *
| 11.0 0.0 |
| 21.0 23.0 |
AC = | 33.0 34.0 |
| 42.0 44.0 |
| 51.0 53.0 |
* *
* *
| 1 1 |
| 1 3 |
KA = | 3 4 |
| 2 4 |
| 1 3 |
* *
N = 4 NT = 3
* *
| 11.0 21.0 51.0 0.0 |
| 42.0 0.0 0.0 0.0 |
AT = | 33.0 23.0 53.0 0.0 |
| 34.0 44.0 0.0 0.0 |
| 0.0 0.0 0.0 0.0 |
| . . . . |
* *
* *
| 1 2 5 1 |
| 4 1 1 1 |
KT = | 3 2 5 1 |
| 3 4 1 1 |
| 1 1 1 1 |
| . . . . |
* *
This subprogram computes the matrix-vector product for square sparse matrix A, stored in compressed-diagonal storage mode, using either the matrix or its transpose, and vectors x and y:
where A, x, and y contain long-precision real numbers.
| Fortran | CALL DSDMX (iopt, n, nd, ad, lda, trans, la, x, y) |
| C and C++ | dsdmx (iopt, n, nd, ad, lda, trans, la, x, y); |
| PL/I | CALL DSDMX (iopt, n, nd, ad, lda, trans, la, x, y); |
If iopt = 0, matrix A is a general sparse matrix, where all the nonzero diagonals in matrix A are used to set up the storage arrays.
If iopt = 1, matrix A is a symmetric sparse matrix, where only the nonzero main diagonal and one of each of the unique nonzero diagonals are used to set up the storage arrays.
Specified as: a fullword integer; iopt = 0 or 1.
If trans = 'N', A is used in the computation.
If trans = 'T', AT is used in the computation.
| Note: | No data should be moved to form AT; that is, the matrix A should always be stored in its untransposed form. |
Specified as: an lda by (at least) nd array, containing long-precision real numbers; lda >= n.
If trans = 'N', A is used in the computation.
If trans = 'T', AT is used in the computation.
Specified as: a single character; trans = 'N' or 'T'.
Specified as: a one-dimensional array of (at least) length nd, containing fullword integers; 1-n <= LA(i) <= n-1.
The matrix-vector product of a square sparse matrix or its transpose, is computed for a matrix stored in compressed-diagonal storage mode:
where:
It is expressed as follows for y <-- Ax:
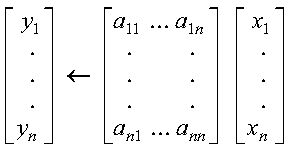
It is expressed as follows for y <-- ATx:
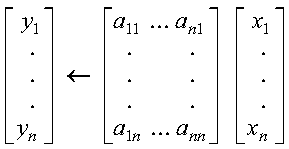
If n is 0, no computation is performed; if nd is 0, output vector y is set to zero, because matrix A contains all zeros.
None
This example shows the matrix-vector product using trans = 'N', which is computed for the following sparse matrix A of order 6. The matrix is stored in compressed-matrix storage mode in arrays AD and LA using the storage variation for general sparse matrices, storing all nonzero diagonals. Matrix A is:
* *
| 4.0 0.0 7.0 0.0 0.0 0.0 |
| 3.0 4.0 0.0 2.0 0.0 0.0 |
| 0.0 2.0 4.0 0.0 4.0 0.0 |
| 0.0 0.0 7.0 4.0 0.0 1.0 |
| 1.0 0.0 0.0 3.0 4.0 0.0 |
| 1.0 1.0 0.0 0.0 3.0 4.0 |
* *
IOPT N ND AD LDA TRANS LA X Y
| | | | | | | | |
CALL DSDMX( 0 , 6 , 5 , AD , 6 , 'N' , LA , X , Y )
* *
| 4.0 0.0 0.0 0.0 7.0 |
| 4.0 0.0 0.0 3.0 2.0 |
AD = | 4.0 0.0 0.0 2.0 4.0 |
| 4.0 0.0 0.0 7.0 1.0 |
| 4.0 0.0 1.0 3.0 0.0 |
| 4.0 1.0 1.0 3.0 0.0 |
* *
LA = (0, -5, -4, -1, 2) X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)
Y = (25.0, 19.0, 36.0, 43.0, 33.0, 42.0)
This example shows the matrix-vector product using trans = 'N', which is computed for the following sparse matrix A of order 6. The matrix is stored in compressed-matrix storage mode in arrays AD and LA using the storage variation for symmetric sparse matrices, storing the nonzero main diagonal and one of each of the unique nonzero diagonals. Matrix A is:
* *
| 11.0 0.0 13.0 0.0 15.0 0.0 |
| 0.0 22.0 0.0 24.0 0.0 26.0 |
| 13.0 0.0 33.0 0.0 35.0 0.0 |
| 0.0 24.0 0.0 44.0 0.0 46.0 |
| 15.0 0.0 35.0 0.0 55.0 0.0 |
| 0.0 26.0 0.0 46.0 0.0 66.0 |
* *
IOPT N ND AD LDA TRANS LA X Y
| | | | | | | | |
CALL DSDMX( 1 , 6 , 3 , AD , 6 , 'N' , LA , X , Y )
* *
| 11.0 13.0 0.0 |
| 22.0 24.0 0.0 |
AD = | 33.0 35.0 0.0 |
| 44.0 46.0 0.0 |
| 55.0 0.0 15.0 |
| 66.0 0.0 26.0 |
* *
LA = (0, 2, -4) X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)
Y = (125.0, 296.0, 287.0, 500.0, 395.0, 632.0)
This example is the same as Example 1 except that it shows the matrix-vector product for the transpose of a matrix, using trans = 'T'. It is computed using the transpose of the following sparse matrix A of order 6, which is stored in compressed-matrix storage mode in arrays AD and LA, using the storage variation for general sparse matrices, storing all nonzero diagonals. It uses the same matrix A as in Example 1.
IOPT N ND AD LDA TRANS LA X Y
| | | | | | | | |
CALL DSDMX( 0 , 6 , 5 , AD , 6 , 'T' , LA , X , Y )
AD =(same as input AD in Example 1) LA =(same as input LA in Example 1) X =(same as input X in Example 1)
Y = (21.0, 20.0, 47.0, 35.0, 50.0, 28.0)