li
xi ui After your problem has been loaded into the Optimization Library workspace, you can solve it by calling one (or more) of the solver subroutines. You can certainly call a solver without adjusting any of the control variables or worrying about how the solution is obtained. However, you may want to fine-tune the operation with control variables, or modify the solve algorithm. For example, with user exit routines you can create your own branch-and-bound algorithm for mixed-integer programming problems.
This chapter explains how to use library modules for such complex problems. It describes the algorithms used for linear programming problems, both simplex and interior-point barrier methods, mixed-integer programming problems, pure network programming problems, and quadratic programming problems. After describing each algorithm, related control variables are listed with explanations. The subroutines described in this chapter are:
|
Note: |
The descriptions given below are only outlines of the algorithms used. They are for informational purposes only and should not be considered as more than that. |
In linear programming, both the objective function and the constraints are linear. Two methods are provided to solve linear programming problems: simplex and interior-point barrier. These methods are described below.
The simplex algorithm was developed by George Dantzig, and published in 1947. While the implementation of the algorithm has undergone major modification, the underlying concept has withstood the test of time. For many linear programming problems, the simplex method is still the best method.
You may treat EKKSSLV as a black box that you simply call and get the results. In most cases this should be satisfactory. However, if you know how your problem is structured, you can consider customizing the following two places where simplex algorithms typically spend most of their computational time.
There is a trade-off between steps 1 and 2. When you have an all logical basis, step 1 takes very little time so you want to spend as little time as possible in step 2. In other words, early on iterations are fast, so do a lot of them without worrying about getting the best pricing output. Later on, when iterations become expensive, you will want to carefully choose an incoming variable to control step 2. You can control this pricing transition with the init parameter to EKKSSLV and the control variables described later in this section. The following is a brief description of the primal simplex algorithm, as implemented in the Optimization Library, followed by a discussion of the related control variables.
The primal simplex method as implemented in the library follows the revised simplex method given by Dantzig, with many variations. The problem Ax = b is broken down into ABxB + ANxN = b where AB is an m × m square matrix whose components are the coefficients of the basic variables in the constraint relations, xB is a vector of length m, xN is a vector of length n - m, and AN is an m × (n-m) matrix whose components are the coefficients of the nonbasic variables in the constraint relations.
EKKSSLV tries to combine phase 1 and phase 2 so that a small amount of the phase 2 objective is used. That is, a composite objective function, consisting of the value of the real control variable Rpweight * feasible objective + infeasible objective, is used.
The random heuristic assumes that all the reduced costs from the previous iteration are correct and chooses a variable from a random subset. If the actual reduced cost has the correct sign, then the variable is chosen. If not, then all reduced costs are recomputed and a variable with a reduced cost of the correct sign is found. If the success rate is low, or the size of the representation of the inverse becomes too large, then a switch is made to Devex pricing.
For example, a problem that has not been scaled, might have a variable with costs and element entries of 1000. This variable might have a reduced cost of 1000. A second variable with entries of 1 could have a reduced cost of 1. In other words, the first variable has a reduced cost 1000 times the second, but the second could be increased 1000 times. The two variables actually have equal value even though the first has a much greater reduced cost.
This problem can be overcome by simple scaling, however, in the simplex method the "frame of reference" that is, the basic variables, keep changing. The Devex heuristic attempts to scale variables according to a fixed frame of reference. To do this exactly, as in the method of steepest descent, effectively involves computing the norm of each updated column. Devex instead computes this norm once and then approximates it. If the approximation becomes unreliable, it is recomputed exactly and the approximation begins again.
Goldfarb and Reid give a method for computing the exact norms that involves approximately twice as much work as the Devex approximation. With the computer architectures in the IBM Vector Facility and the RISC System/6000 workstation, the cost of the extra computation is significantly reduced. The integer control variable Idevexmode can be set to specify computing and using these more accurate scale factors. See the description of Idevexmode in the related control variable list at the end of this section.
Devex pricing vectorizes very well. If you have an IBM Vector Facility, the library modules will take advantage of it. This makes Devex attractive in some cases. EKKSSLV makes appropriate decisions based on your hardware and the problem characteristics. You can control the change to Devex with the init parameter of EKKSSLV and with the integer control variable Ifastits, which is discussed later on in this section.
|
Note: |
If the problem is found to be primal degenerate, then the RHS is slightly perturbed, the modified problem is solved, and then the dual algorithm is used to solve the problem with the original RHS. |
All the commentary given above applies to the primal version of the simplex
method. For most cases the primal algorithm will be the preferred method.
However, you will be informed (by an output message), if the problem is primal
degenerate. If that is the case, and the problem takes many iterations to
solve, it may be worth trying the dual algorithm. It may also make sense if
the problem starts dual feasible. A true dual algorithm is implemented with
a phase 1, phase 2, and a composite phase 1/2. Be aware that the primal algorithm
is slightly more accurate, and in pathological cases, EKKSSLV may decide to
switch back to the primal algorithm.
|
Note: |
If the problem is dual degenerate, then the objective is slightly perturbed, the modified problem is solved, and then the primal algorithm is called to solve the problem with the original objective. |
This section lists the control variables related to the simplex algorithm. The primal simplex algorithm is robust. It benefits from an excellent sparse factorization algorithm. For most problems, you can achieve 90% of optimal performance using the default settings.
For complete information on all the integer and real control variables,
refer to Appendix C. "Control Variables".
The contents of arrays pointed to by index control variables may change during
execution. For information about these control variables, refer to "EKKNGET
- Request Current Start Indices of OSL Information".
|
Note: |
maxint refers to the maximum allowable integer value on your platform, and maxreal refers to the maximum allowable real value on your platform. |
Description: The log frequency.
Description: The maximum number of iterations before a refactorization (invert) of the basis must be performed.
Description: The maximum number of iterations that will will be performed.
Description: The simplex log detail bit mask.
Iloglevel controls how much
information is printed for each log message.
For information on bit
masks, see "Control
Variable Bit Masks"
Description: The stopping condition bit mask.
Description: The type of Devex pricing to be used.
Description: The current number of primal infeasibilities.
Description: The current number of dual infeasibilities.
Description: The fast iteration switch.
Description: The problem status.
Description: The allowed amount of primal infeasibility.
Description: The allowed amount of dual infeasibility.
Description: The weight of the linear objective.
Description: The multiplier
of the feasible objective that is used
when the current solution is
primal infeasible.
Description: The rate of change for Rpweight or Rdweight.
Description: The proportion
of the feasible objective that is used
when the current solution
is dual infeasible.
Description: The value of the objective function.
Description: The sum of the primal infeasibilities.
Description: The sum of the dual infeasibilities.
The barrier method implemented in EKKBSLV is a primal-dual barrier method with predictor-corrector. In this chapter we give a brief overview of interior point methods, and then describe in more detail the method implemented in EKKBSLV.
Barrier methods are interior point methods - as opposed to the simplex method, which proceeds by moving along the edges of the polytope of feasible solutions.
minimize: cTx
subject to:
Ax = b
li xi ui
Replacing the inequality constraints by a logarithmic barrier function gives the following, which is the problem actually solved.
minimize: Sj {cj xj - m ln ( xj - lj ) - m ln ( uj - xj ) }
subject to: Ax = b
where the parameter m tends to zero from above. The initial value of m is an arbitrary small number (default value typically 0.1) which is scaled internally to take into account the scale of the objective function.
The primal interior-point method (see Gill et al.) takes the direction of steepest descent from the current solution, then projects it so that the projected direction p is in the null space of the equality constraints. However, such methods have been superseded by primal-dual methods.
Primal-dual methods work simultaneously with both the primal problem and its dual. This has great advantages because the relationship between the primal and dual problems is well known.
The dual problem (for a general LP with upper and lower bounds) is:
maximize:
bT
y + lT z -
uT w
subject to:
AT y + z - w = c
z 
0
w 0
where the vector y contains the dual variables corresponding to the rows of A, and the vectors z and w are the dual variables corresponding to the lower and upper bounds on the primal variables in the vector x. In addition, l is the vector of lower bounds, and u is the vector of upper bounds. This dual problem has an equivalent barrier formulation:
maximize: bTy + l T z - uT w + m Sj ln zj + m Sj ln wj
subject to:
ATy + z - w = c
as m
goes to 0.
For a given m, necessary conditions for the existence of a solution of this pair of barrier problems can be derived from their Lagrangians (see Lustig et al.). These conditions are:
Ax = b
x - s = l
x + t = u
ATy
+ z - w = c
SZe = me
TWe = me
where s and t are the slacks on the lower and upper bounds of x, and S, T, Z, and W are the diagonal matrices with elements sj, tj, zj, and wj, respectively. Note that the product terms SZ and TW are nonlinear.
The primal-dual method partially solves the equations for the necessary conditions for a sequence of m values that converges to 0. This is done in such a way that if the primal and dual problems are both feasible, the two sequences of solutions will converge toward optimality.
For each fixed m, Newton's method is applied. This yields:
ADx = b
- A x
Dx - Ds = 0
Dx +Dt = 0
AT y
+ Dz -Dw
= c - AT y - z +
w
ZDs + SDz = - SZe + me
WDt + TDw = - TWe + me
These are used to obtain the primal and dual directions Dx, Dy, Dz andDw. The critical step in solving this system is the solution of a set of equations of the form:
A ( S -1 Z + T -1 W ) -1 AT D y = v
Here v is a complicated but easily computed vector, and when Dy is obtained, Dx, Dz, and Dw are calculated by direct substitution.
The critical system to be solved (for Dy) requires the Cholesky factors of this matrix, which has the nonzero structure of AAT, with perhaps the dense columns of A omitted (see below).
The positions of the nonzeros in AAT are computed in one of two ways based on the integer control variable Iadjactype:
A minimum degree row ordering routine is used to reduce the fill-in of nonzeros during Cholesky factorization. The row ordering is used as input to a symbolic factorization routine that computes the positions of the nonzeros in the factors. The ordering is maintained as a static data structure, following the technique used in George and Liu. You can control the ordering process with two integer control variables: Iroword and Iordunit.
If Iroword = 0,the ordering is left unchanged. If Iroword is set to 1, a minimimum degree row ordering is computed and written to logical unit Iordunit, if this control variable has been set to a valid positive value. If the value of Iroword is 2, the ordering is done by a user exit subroutine named EKKORDU. If the value of Iroword is 3, a row ordering algorithm based on graph partitioning, developed by Anshul Gupta, is used to do the row ordering. (This is the default value.) If the value of Iroword is 4, Gupta's graph partition based row ordering algorithm is used, and in addition, a multifrontal sparse solver is used for the Cholesky decomposition. (This algorithm requires more storage than that used when the value of Iroword is 3, but usually less storage than that used when the value of Iroword is 1. It may be faster on IBM Power-2 RISC 6000 workstations, but it may be slower on Intel based machines.) If the value of Iroword is -1, an attempt is made to read the ordering from logical unit Iordunit. This enables you to avoid the potentially expensive step of determining a new row ordering when solving a variant of a problem previously solved. Note: specifying an invalid ordering causes a new minimum degree ordering to be computed.
In practice, the lower right part of the Cholesky triangular factor L is quite dense, and it can be more efficient to treat it as 100% dense. This is controlled by the parameter Rdensethr (default value 0.7). When the symbolic factorization encounters a column of L that has at least this proportion of nonzeros, the remainder of L is treated as dense.
The required system is solved by factoring the normal matrix A ( S -1 Z + T -1 W ) -1 AT . This normal matrix may be formed by one of two methods:
The accuracy of the projection is critical to the success of the method. Since linear programming problems often have linearly dependent rows, the normal matrix will often be rank deficient and usually ill-conditioned. The control variables that affect Cholesky factorization are Rcholabstol, Rcholtinytol (2), Rdiagpert, and Idroprowct.
Two tolerances are provided to control the factorization. First, the matrix D2 is scaled so that its largest value does not exceed 1015. If the diagonal (pivot) element falls below Rcholabstol, then it is set to the value of Rcholabstol. However, if the value is even smaller-below Rcholtinytol-the row is treated as dependent and ignored in the factorization. The default value for Rcholabstol is 10-15, and for Rcholtinytol it is 10-18.
A third parameter is sometimes useful in controlling the factorization. When the diagonal element for a particular row has been rejected Idroprowct consecutive times, the row is declared redundant (free) for the remainder of the barrier algorithm. The default value for Idroprowct is 1, causing rows to be freed as soon as diagonals are rejected.
If dense columns are present in A, a preconditioned conjugate gradient method may be used. This method is discussed in Paige and Saunders. However, it is strongly recommended that the "regularized" form of the problem be solved instead.
The importance of accuracy in the Cholesky factor and the mechanisms for controlling it are exactly the same as in the primal method.
When the direction vector has been computed, primal and dual step lengths ar and ad must be computed in such a way that the variables x, z, and w are prevented from violating their bounds. These are then multiplied by a step-length multiplier, whose value must be less than that of m. The default value of this multiplier is usually 0.99995. Note that this value is usually much closer to 1.0 than the value used in the primal method. A new solution point is defined by:
x 
x + ar Dx
y y + ar Dy
z z + ad Dz
w
w + ad Dw
The barrier parameter m is chosen internally by formula as detailed by Lustig et al, formulas (10-14)).
Optimality is declared when the primal and dual problems are both feasible and the primal and dual objectives are sufficiently close, as determined by an acceptible tolerance. The primal infeasibility is defined to be the worst violation of the primal constraints divided by the largest primal variable value, that is
max j | bj - A*
j x |
_________________
max j | xj |
The dual infeasibility is similarly defined as the worst violation of the
dual constraints, scaled by the largest dual variable, that is
max j | cj - A
*jT y + z
j - w j |
________________________
maxj | yj |
The problem is said to be primal feasible if the primal infeasibility is less than a specified tolerance, and similarly dual feasible, if the dual infeasibility is less than another specified tolerance.
Agreement of the primal and dual objectives is determined by yet another tolerance. If the relative difference of the two objectives (assuming the primal is being minimized), that is
cTx - bTy - lTz + uTw
____________________
1 + | bT
y + lTz - uTw |
falls below the value of the tolerance for this gap (default value 10-7), and the problem is both primal and dual feasible, optimality is declared. If through some numerical difficulty the primal value falls below the dual value, the algorithm is abandoned.
Convergence may be strongly influenced by the use of scaling and presolving. It is recommended that problems be presolved as a matter of course, to reduce both iteration count and rank deficiency problems.
The predictor-corrector method is a variation of the primal-dual method originated by S. Mehrotra. It usually requires fewer iterations than the standard primal-dual method, and is currently the interior point method supported in OSL. It differs from the basic primal-dual method in three important ways:
These differences are made evident by output messages that indicate a loss of accuracy in the direction vector and in the worst bound violation.
The predictor-corrector method does not attempt to solve the necessary conditions by Newton's method, but by a direct approximation method. Let Ds, Dt, Dw, Dx, and so forth be the modifications to the current solution, s, t, w, x, y, and z, required to solve for the current value of m. These vectors satisfy:
ADx = b - Ax
Dx - Ds
= 0
Dx + Dt
= u - x - t
AT Dy
+ Dz - Dw
= c - A Ty - z +
y
ZDx + SDz = me
- SZe -DS DZ
WDt + T Dw = me
- TWe - DT DW
where DS, DT, DW, and DZ are the diagonal matrices with entries Ds, Dt, and so forth.
The product terms DX DZ and DT DW make this system nonlinear. They are approximated (predicted) by solving a related system (known as the affine system) in which both the product terms and the terms that involve m have been omitted:
A
Dxp = b - Ax
Dxp
- Dsp =
0
Dxp
+ Dtp =
u - x - t
AT
Dyp + Dzp - Dwp
= c - AT y
- z + w
ZDxp
+ S Dzp
= -SZe
WDtp
+ T Dwp
= - TWe
The predicted values, Dsp, Dtp, and so forth, produced by this predictor step are checked for accuracy, and a step-length calculation is performed to make sure that they preserve feasibility. If necessary, scaled back values are used to recompute a suitable value for m. The resulting predicted values are then plugged in to the right-hand side of the actual system:
ADx
= b - Ax
Dx - Ds
= 0
Dx + Dxt
= u - x - t
A T Dy + Dz
- Dw = c - A T y - z + w
Z Dx
+ S Dz = me - SZe - DSpDZp
W Dt
+ T Dw = me -TWe - DTpDWp
This system is then solved to obtain the corrected directions Ds, Dt, and so on. (Here DSp, DTp, and so on, are diagonal matrices with the vectors Dsp, Dtp, and so on, as their diagonals.) The solution of the corrector step is also checked for accuracy (and refined if necessary) before computing the step length and updating the solution as in the standard primal-dual method-with one difference: the slacks, t, on the violated upper bounds are updated by Dt, independently of Dx, until the bounds are satisfied.
minimize: cTx + 0.5 || g x|| 2 + 0.5 || p|| 2
subject to:
A x + d p = b ,
and
li xi ui
for each i.
Details of the algorthmic treatment of such problems are given in Saunders and Tomlin, but for the outline presented here it is worth noting that the necessary conditions, as reduced from a modification of those used in the Predictor-Corrector method shown above, can be represented by the KKT System:
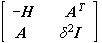
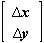
where H = S -1 Z + T -1 W + g 2 I.
This form may be reduced (by block pivoting on H) to a normal form almost identical to that used in the primal-dual predictor-corrector method described above. However, the algorithm used for the regularized problem can solve the KKT system explicitly, or block pivot only on the portion of H corresponding to sparse columns of A. This leads to a reduced KKT system that retains the dense columns of A, which is then solved explicitly. This is now the preferred method for handling dense columns in the interior point code.
Default values of g = d = 0.001 are satisfactory for most problems, especially if EKKBSLV (with the algorithm parameter of its calling sequence set to -1) is followed by a crossover to the simplex method. It is usually safe to use smaller values of these parameters, which leads to a solution of the regularized problem that is closer to that of the original problem. However if the values are too small, the algorithm may break down. Some experimenting with different values may be useful. It is particularly important to scale the constraint matrix of the problem.
The regularized LP problem is of course a simple form of quadratic programming problem. With just a slight extension, the algorithm can be used to solve regularized quadratic programming problems of the form:
minimize: cT x + 0.5 xT Q x + 0.5 || p || 2
subject to:
A x + d p = b ,
and
li xi ui
for each i.
Here Q = Q0 + || g x||2 and the matrix Q0 is the quadratic coefficient matix of the problem to be solved. The algorithmic procedure is very similar to that outlined above for regularized LP problems, except that now the matrix H in the KKT system is of the form H = S -1 Z + T -1 W + Q, and any column of A corresponding to a non-trivial column of Q is treated as if it were dense, that is, it is explicitly included in the reduced KKT system.
The comments on the regularization parameters and scaling apply as in the case of regularized LP.
The (interior) regularized QP method is invoked by calling EKKQSLV with the algorithm option set equal to -1.
For most LP problems, you should first call EKKPRSL, and then call EKKBSLV with alg=0 and sslvswch=0. If you need only the optimal solution and optimal objective value, the call to EKKBSLV may be followed by a call to EKKPSSL. This will yield optimal, complementary, primal and dual solutions to the problem.
If you need a basic feasible solution to the problem for input to EKKSOBJ, EKKSPAR, EKKMSLV or for some other purpose, the call to EKKBSLV should have sslvswch<0. Since EKKPSSL does not do any refactorization or optimization, the call to EKKPSSL may need to be followed by a call to EKKSSLV to get an optimal basis.
This section lists the control variables related to the interior-point barrier method.
For complete information on all the integer and related control variables,
refer to Appendix C. "Control Variables".
The contents of arrays pointed to by index control variables may change during
execution. For information about these control variables, refer to "EKKNGET
- Request Current Start Indices of OSL Information".
|
Note: |
maxint refers to the maximum allowable integer value on your platform, and maxreal refers to the maximum allowable real value on your platform. |
Description: The maximum number of iterations of the interior-point barrier algorithm.
Description: The formation of the adjacency matrix AAT.
Description: The formation of the normal matrix.
Description: The dense column threshold.
Description: The null space checking switch.
Description: The constraint dropping threshold.
Description: The potential basis flag.
Description: The maximum refinement attempts.
Description: The problem status.
Description: The row ordering method indicator.
Description: The row ordering read and write logical unit.
Description: The current number of iterations EKKBSLV has performed.
Description: The allowed amount of primal infeasibility.
Description: The allowed amount of dual
infeasibility. This variable is the
dual equivalent of the primal variable Rtolpinf.
Description: The weight of the linear objective.
Description: The tolerance for fixing variables in the barrier method when infeasible.
Description: The tolerance for fixing
variables in the barrier method
when feasible.
Description: The absolute pivot tolerance for Cholesky factorization.
Description: The cut-off tolerance for Cholesky factorization.
Description: The multiple of m to add to the linear objective.
Description: The projection error tolerance.
Description: The value of the objective function.
Description: The density threshold for Cholesky processing.
Description: The value of the dual objective for EKKBSLV.
Description: The barrier method primal-dual gap tolerance.
Description: The primal-dual barrier method step-length multiplier.
Description: The diagonal perturbation for Cholesky factorization.
Pure network programming problems are linear programming problems in which the columns of the constraint matrix have exactly two nonzero elements, one equal to 1 and the other equal to -1. The columns of a pure network problem are known as arcs, and the rows are known as nodes. The pure network problem that EKKNSLV solves is given by:
minimize
cT x
subject to:
lri Ai*
uri
for i = 1 to m
lcj xj ucj
for j = 1 to n
where:
For the network problem, lri and uri give bounds for the exogenous flows, and the values of the variables xi are the arc flows.
For network problems, the primal network simplex algorithm is significantly faster than the general-purpose primal simplex algorithm in EKKSSLV. This is because basis factorizations are not needed. The majority of the processing time is spent computing reduced costs (or "pricing"). Therefore, the pure network solver allows you to select a pricing strategy that is best suited for your application.
EKKNSLV transforms the problem defined above into one with equality constraints by adding slack arcs. Since adding these arcs increases the size of the problem, performance is best for problems with only equality constraints. The objective function is a composite objective function similar to that used in EKKSSLV. A penalty cost d is given to each artificial arc, and d is gradually increased until feasibility is reached.
The steps of the algorithm are as follows:
By default the starting basis is an all artificial basis. However, if you are restarting EKKNSLV, or have saved an advanced basis with EKKBASO, you can start EKKNSLV with that advanced basis.
Verifying that the dual solution is feasible involves computing the reduced
cost vector
( cN - uAB ), where cN
is the vector of costs for the nonbasic variables and AB
is the matrix of nonbasic columns. The current solution is optimal only if
this vector has nonnegative values for variables that are at their lower bound,
or nonpositive values for variables that are at their upper bound.
The orientation of an arc in a path determines whether its flow will increase or decrease.
The dual algorithm contains no Phase 1 procedure. All arc costs for the problem must be nonnegative on entry to EKKNSLV. The algorithm maintains dual feasibility throughout and works toward primal feasibility by pivoting. The dual algorithm is quite similar to the primal algorithm. The steps are as follows:
The pure network solver handles certain pure networks by use of special code. Maximum flow problems and shortest path problems are automatically detected and solved by highly efficient, nonsimplex methods. The following briefly describes maximum flow and shortest path problems and describes how to formulate these problems so that their structure will be recognized.
Maximum flow problems are used to determine the maximum that can flow between two nodes in a network. As with all pure networks, the columns of the constraint matrix for a maximum flow problem correspond to arcs in a directed graph, and rows correspond to nodes. One node is identified as the source, and another is the sink. The maximum flow that can be sent through the network from the source to the sink can be determined by maximizing the flow that can be put on a single "return" arc from the sink to the source. If one arc in a pure network (the return arc) has a cost of -1 and all other arcs have a cost of 0, EKKNSLV uses the head and tail of the return arc to identify the source and sink of a maximum flow problem. If, in addition to having the return arc, the pure network has equality constraints, and the exogenous flows (or right-hand sides) are all zero, the network is solved as a maximum flow problem using special code. The optimal value of the objective function gives the maximum flow, and the solution vector gives flows on the arcs that yield the maximum flow.
Shortest-path problems yield a shortest path through a directed graph from a starting node to a termination node. The length of a path is given by the sum of the lengths of the arcs in the path. The lengths of the arcs are typically given by their costs. Event scheduling, as well as trip optimization, can be formulated as shortest-path problems. If a network has one node (the starting node) with an exogenous flow of 1 and one node (the termination node) with an exogenous flow of -1 and all other exogenous flows are 0, EKKNSLV will detect a shortest-path structure in the problem and solve the problem by use of special code. The capacities of the arcs must also be greater than or equal to infinity (1031). An arc is part of the shortest path returned by EKKNSLV if it has a flow of 1 in the optimal solution, and arcs with a flow of 0 are not part of the path.
This section lists the control variables related to the network simplex method.
For information on all the integer and related control variables, refer
to Appendix C. "Control Variables".
The contents of arrays pointed to by index control variables may change during
execution. The index control variables Narcid, Nlevel, Nparent,
Npreorder, and Nrevpreorder can be used to access tree data
structures. For a description of the tree data structures, see Kennington
and Helgason. The regions accessed with Ncolsol, Nrowsol,
Nrowduals, and Ncolrcosts contain the appropriate primal or
dual solution vectors after EKKNSLV finds an optimal solution. For complete
information about these control variables, refer to "EKKNGET
- Request Current Start Indices of OSL Information".
|
Note: |
maxint refers to the maximum allowable integer value on your platform, and maxreal refers to the maximum allowable real value on your platform. |
Description: The log frequency.
Description: The current number of iterations
that have been performed
in a solver subroutine.
Description: The maximum number of iterations that will be performed.
Description: The current number of primal infeasibilities.
Description: The current number of dual infeasibilities.
Description: The problem status.
Description: The type of pricing for EKKNSLV.
Description: The weight of the linear objective.
Description: The value of the objective function.
Description: The sum of the primal infeasibilities.
Description: The sum of the dual infeasibilities.
Description: The sample size for the EKKNSLV pricing algorithm.
Description: The Fortran index into mspace for the first
element of the indices of the arcs in the basis.
Description: The Fortran index into mspace for the first
element of the array of node levels.
Description: The Fortran index into mspace for the first
element of the array of parent nodes.
Description: The Fortran index into mspace for the first
element of the preorder traversal array.
Description: The Fortran index into mspace for the
first element of the reverse preorder traversal array.
A mixed-integer programming problem is a mathematical programming problem in which some of the variables are restricted to integer values. EKKMSLV is capable of handling mixed-integer programming problems with linear constraints and an objective function that is either linear or quadratic. When all the integer variables must be either 0 or 1, the problem is called the mixed 0-1 problem. A pure integer problem is one for which all the variables may take only integer values. A pure 0-1 integer problem is one in which all the variables must be integers, and their only possible values are 0 and 1.
In this section, strategies for solving mixed-integer programming problems are discussed. These strategies involve branch-and-bound and supernode processing. Branch-and-bound is discussed first, followed by EKKMPRE's supernode preprocessing and the data structures used in both these strategies. Next, there is an explanation of node choice and branching strategies, and of EKKMSLV supernode processing. This explanation includes pointers to information about user exit subroutines. The solution of some difficult problems may require the use of user exit subroutines. Finally, there is a list of control variables related to mixed-integer programming.
Both linear and quadratic mixed-integer programming problems are solved by a branch-and-bound method. The choice of linear or quadratic solver is made in one of the user exit subroutines EKKEVNU and EKKSLVU, as discussed in Chapter 20. The basic idea of branch-and-bound is simple, especially for the mixed 0-1 case.
For the 0-1 case, first form a relaxed problem where the 0-1 conditions
are relaxed to 0 xj
1 for the integer variables
xj This becomes node 0 and is an active
node. The outline of the algorithm for creating a tree of linear or quadratic
programming problems on which to branch-and-bound is:
Initially in step 1, node 0 is the only active node. If there are no active nodes at some subsequent time, then the problem has been solved and the current best integer solution is optimal. The criterion for the choice of node is discussed in "Choosing a Node".
In step 2, the three cases correspond to three outcomes:
The preceding discussion is for the case when all integer variables are 0-1. Integer variables may also have integer lower and upper bounds other than 0 and 1. A variable might have a lower bound of -2.0 and an upper bound of 2.0, and be allowed to take the values -2, -1, 0, +1 and +2. The algorithm is easily extended. If the value of a variable was 1.7, then the two branches would involve reducing the upper bound to 1.0 on one branch (the down branch) and increasing the lower bound to 2.0 on the other branch (the up branch).
For special ordered sets (SOS), the branches are more powerful. The variables in such a set are in order, and all variables before a certain point in the sequence can be set to zero on a specified branch - forcing the solution to lie in the upper part of the set, or all the variables beyond a certain point can be set to be zero - forcing the solution to lie in the lower branch. The branch point is given as a reference row value.
One use of special ordered sets is to model economies of scale. An example
is where there is a possibility of building a warehouse, where the cost of
building is:
|
Size |
Cost |
|
0 |
0 |
|
10 |
5 |
|
30 |
10 |
|
60 |
15 |
|
120 |
25 |
This can be modeled as a cost of:
5l1 + 10 l2 + 15 l3 + 25 l4
where the actual capacity is represented by:
10l1 + 30l2+60 l3 + 120 l4
and the capacity row is:
l0 + l1 + l2+ l3+ l4 = 1
If the warehouse must be one of the above sizes then only one of the l may be nonzero, while if intermediate sizes are allowed then two adjacent l may be nonzero (summing to one).
If the warehouse has to be one of the given sizes, the variables could be declared to be 0-1. Then a branch might be to build a warehouse of size 60 or do not build it. If the variables are declared to be a special ordered set of type 1, then one branch might be to build a warehouse of size 30 or below, while the other branch would be to build a warehouse of size 60 or above. This is a more powerful binary choice.
For this to happen, the variables have to be ordered, but to make the best choice of branch, it is useful to know where to branch to do the most good.
If in the continuous solution l0
had value 0.7 and l4 had value 0.3,
then the available capacity is
0.3 × 120 which is 36. This suggests that a sensible branch might be
the one described above. For this branch to be implemented, a specification
of the capacity row is required. (This is also called the "reference" row.)
For the Optimizaton Library modules, such a reference row need not be a part
of the linear constraints of the problem. . (See
Beale.)
The definition of reference row used here is: A set of real values, one for each member of the set, that give by their values the ordering of the set. At any solution, the sum of the product of the solution values with the reference entries is computed and divided by the sum of the solution values (normally 1.0). This gives a branch point in the set. For special ordered sets of type 2 this point is adjusted to the nearest reference entry, while for other types it is adjusted to be halfway between two reference points.
The subroutine EKKMPRE allows you to preprocess the data structures of mixed-integer programming problems with a linear objective function. EKKMPRE cannot be used to preprocess mixed-integer programming problems with a quadratic objective function. This preprocessing reduces the size of the initial branch-and-bound tree by performing analysis based on the 0-1 structure of the problem. It also optionally causes a simpler form of this analysis to be performed at some nodes when EKKMSLV is called. This analysis is referred to as supernode because it is comparable to analyzing many nodes of the branch-and-bound tree at once.
|
Note: |
EKKMPRE attempts to add additional rows. Therefore, you should allow additional space for extra rows if you use EKKMPRE. To do this, set the integer control variable Imaxrows to the negative of the number of rows to be added, after calling EKKDSCM but before calling EKKMPS. |
The analysis performed by EKKMPRE is as follows:
On some problems, particularly small ones, the time required for the extra work done by EKKMPRE may result in longer solution time. Specifically, EKKMPRE can be thought of as having a processing time on the order of k2 to k3 , where k is the number of nonzero elements in the matrix, whereas EKKMSLV without EKKMPRE preprocessing and supernodes has a processing time on the order of 2n, where n is the number of integer variables. If it appears that EKKMPRE will take more time than normal branch-and-bound, remove the call to EKKMPRE before the call to EKKMSLV.
Several control variables can affect the processing done by EKKMPRE and EKKMSLV. Istrategy, integer control variable #52, provides some control over the work done by EKKMPRE when preprocessing and by EKKMSLV when processing supernodes. Istrategy is a bit mask. For information on using mask control variables, see "Control Variable Bit Masks". The meanings of the various bit settings for this control variable are explained in Appendix C. "Control Variables".
It is difficult to predict which, if any, of the approaches provided by the various settings for Istrategy will improve performance on a particular problem, but advanced users with particularly difficult problems may want to experiment with different options. The default setting for Istrategy was chosen to provide best overall performance, but there are many problems for which changing the value of Istrategy can significantly improve performance. On the other hand there are also many problems for which using these options could actually degrade performance. If you are going to repeatedly solve large, difficult MIP problems from among a closely related set of similar problems in a production environment, then experimenting with different values for Istrategy might prove worthwhile.
The structures that are needed to implement the algorithm are stored in a file. In order to solve the relaxed linear problems, the current bounds on the variables must be available to the solver. This information is kept as a matrix block stored by indices in the workspace, or in the file specified in the munit parameter of the calling sequence for EKKMSLV.
Initially, enough matrix buffers for at least 10 complete sets of bounds are reserved. Branches at levels in the tree that are multiples of 5 have a complete matrix block describing all the bounds that have changed since the continuous solution, while other ones point to a complete block and modify the bounds set since then.
If the buffers become filled then:
Although the solution can proceed without knowledge of the optimal basis for the previous branch, it is more efficient to have this information. In this case, the solution is dual feasible with only one primal infeasibility that corresponds to the variable being branched on.
Bases are stored using buffers. The status of each variable takes 2 bits of storage. If these buffers become full, then a procedure similar to the one above is used, except that the file specified with the bunit parameter to EKKMSLV is used.
EKKMSLV also has information about the active nodes, that is, the nodes that have not yet been evaluated. This information is always kept in storage and consists of information that is used to decide with which node to continue. This is discussed in "Choosing a Node".
There are also fixed arrays that are created by either EKKMPS or EKKIMDL in the high storage section of dspace. These arrays consist of two sections:
k2.
For each variable in the set the following is stored:
If EKKMPRE has been called there will also be the following information in dspace:
The information stored at each node is:
For each set, the estimated degradation is the sum of the values of the set times the down pseudocost, with the largest value of the set excluded, plus the Riweight.
These degradations are summed to give a rough estimate of how much worse the objective will get before a valid solution is reached.
The choice rule used is:
You can override the node choice rule by writing your own subroutine for the EKKCHNU user exit. You may also obtain information about the status of the problem both before branching and after a node is chosen with the EKKNODU user exit. See "Mixed-Integer User Exit Subroutines".
The branching choice is made among all sets with the highest priority (1=highest). Among these, the variable with the worst, best degradation (smaller of up and down degradations) is chosen.
You can override the branch choice rule by writing your own subroutine for the EKKBRNU user exit. You may also obtain information about the status of the problem both before branching and after a node is chosen with the EKKNODU user exit. See "Understanding Mixed-Integer User Exit Subroutines".
Based on the value of the type argument presented to EKKMPRE, EKKMSLV may optionally perform EKKMPRE-like analyses at some nodes of the branch-and-bound tree. Because this analysis can be considered equivalent to processing many branch-and-bound nodes at once, it is referred to as supernode processing.
Supernode processing is performed by EKKMSLV at a node in the branch-and-bound tree if both of the following are true.
If you have written a user exit subroutine for EKKBRNU and it affects the choice of the variable to branch on, supernode processing will not occur.
The supernode processing algorithm is the same as the algorithm described in "Preprocessing the Problem with EKKMPRE", with the exception that at the last step of the algorithm, supernode processing is ended, a binary branch is created, fixed variables are saved, and EKKHEUU is called.
When supernode processing is ended, the branch variable is arbitrarily set to 0.5, and the branch value may be arbitrary.
This section lists the control variables related to mixed-integer programming.
For complete information on all the integer and real control variables, refer to Appendix C. "Control Variables". The contents of arrays pointed to by index control variables may change during execution. For information about these control variables, refer to "EKKNGET - Request Current Start Indices of OSL Information".
Notes:
Description: The log frequency.
Description: The maximum node number created so far.
Description: The EKKMSLV log detail bit mask.
For information on bit
masks, see "Control
Variable Bit Masks"
Description: The maximum number of nodes to evaluate.
Description: The maximum number of feasible integer solutions to find.
Description: The number of integer solutions found so far.
Description: The number of individual integer variables.
Description: The number of sets.
Description: The number of integer variables at fractional values.
Description: The problem status.
Description: The maximum number of integer variables.
Description: The maximum number of sets.
Description: The bit mask that selects various steps of the MIP algorithm.
Description: The maximum amount of integer information.
Description: Number of integer variables that
must be fixed for supernode
processing to continue.
Description: The number of heuristic passes
to be made by EKKMPRE.
This does not affect EKKMSLV supernode
processing.
Description: The number of branches allowed inside
a supernode before
supernode processing ends.
Description: The amount of extra information
that is saved and restored
by the user exit subroutine EKKNODU.
Description: The cutoff for the branch and bound.
Description: The value of the objective function.
Description: The scale factor for all degradation.
Description: The best feasible integer solution found so far.
Description: The weight for each integer infeasibility.
Description: The amount by which a new solution must be better.
Description: This is a target value of the objective for a valid solution.
Description: The integer tolerance.
Description: The best possible solution.
Description: The best estimated solution.
Description: The supernode processing threshold.
The quadratic programming algorithms implemented are designed to solve convex quadratic programming problems with linear constraints. The simplex based algorithm, due to Dantzig, is a generalization of the corresponding algorithm for LP problems. The interior point algorithm is a natural extension of the algorithm used to solve regularized LP problems.
Statement of the Quadratic Programming Problem:
minimize f(x) = cT x + (1/2) xTQx
subject to:
Ax = b
x 0
where:
Let M and N represent the index sets {1 , 2 , ... , m } and {1 , 2 , ... , n }, respectively. Actually, the algorithm includes both upper and lower bounds on the decision variables x, but to simplify the discussion, consider the problem stated above.
A tableau representing the problem is given by:
where I is the identity matrix of dimension m ×
m. The vector on the right,
,
is known as the right-hand side (RHS). The vector x represents the primal solution, the vector y represents the dual solution, and
the vector s represents the dual slack variables (also called reduced costs). The vectors s and x are
complementary, if they satisfy
x j s j = 0
for each j,
1
j n.
The notion of a basis is generalized from that for linear programming to
be a square symmetric nonsingular submatrix:
where M and B are index arrays for the basic rows and columns of A, and A(M,
B) is the submatrix of A with rows indexed by M and columns indexed by B. A solution to the linear
system defined by this tableau is basic if y and x satisfy:
Where xB and cB are the elements of x and c, respectively, indexed by the array B, and y and b are the elements of x and c, respectively, indexed by the array N/B.
The interior point QP algorithm, discussed above, is used used when EKKQSLV is called with the value of alg set to -1. The following discussion applies to the two-stage, simplex based algorithm used when EKKQSLV is called with the value of alg set to 1.
EKKQSLV does not use EKKCRSH to find an advanced basis from which to start (that is, crash). Instead it uses iterative linear programming as a crash procedure. The linear programming problem solved at each iteration has the same constraint system as the quadratic problem, and the objective function is the linearization of the quadratic objective function at the current solution x. (Initially, x = 0.) The linear problem is solved by EKKSSLV, and the optimal solution yields a lower bound for the quadratic problem, since the quadratic problem has a convex objective function. (Because EKKSSLV is used to solve the linear programming problems, EKKSSLV-related control variables can be used to tune performance.) The crash procedure is a decomposition approach because it iteratively builds an approximation to the feasible region of the quadratic programming problem using the solution of a sequence of related linear programming problems. The master problem is given by:
minimize cT Xw + cT Zv + (1/2) ( Xw + Zv )TQ ( Xw + Zv )
subject to:
eT w
= 1
w
0, v
0;
where the lengths of the vectors w and v are equal to the number of columns in X and Z, respectively and e = (1, 1, 1, ... , 1). Each column of the matrix X is a feasible solution to the quadratic problem. Each column of the matrix Z is a feasible ray of the quadratic problem. This has just one constraint and can be solved quickly.
The procedure first obtains a feasible solution to the quadratic programming
problem,
. It uses this solution to construct
a new linear programming problem:
minimize
( c + Q
)Tx
subject to:
Ax = b
x
0
referred to as the subproblem. If the subproblem has an optimal
solution x* then,
( c + Q )Tx*
- (1/2) T Q
is a lower bound on the true quadratic objective function value. Even if
the subproblem does not have an optimal solution, solving it provides
a direction 
hat that can be
used to strictly improve
the current solution . If Q
= 0, then EKKQSLV stops with
a verification that the primal quadratic programming problem is unbounded
below. After the solution of the subproblem, EKKQSLV has a primal feasible
solution
to add to the matrix of solutions
X in the master problem, or a ray to add to the matrix of rays Z in the master
problem, or both a solution and a ray. The master problem is then solved to
optimality. This provides an upper bound on the value of the quadratic
programming problem, because the master problem is equivalent to the original
quadratic program solved over a restricted feasible region. If the optimal
solution to the master problem is the pair of vectors w* and
v*, the subproblem is reformulated using the point
= X w*
+ Z v*.
If, in the course of alternately solving the master problem and the subproblems, the upper and lower bounds on the objective function value become sufficiently close, the decomposition procedure stops. Otherwise, the procedure stops after the combined sizes of the X and Z matrices becomes too large.
After the decomposition has stopped, a complementary basic solution to the original quadratic problem is created from x* = X w* + Z v* in two phases. First, a primal feasible basic solution is formed starting with the last optimal basis from the subproblem and performing pivots on nonbasic variables that correspond to nonzero elements of x*. This is done in one pass over the variables x, after which all nonzero variables are in the current complementary basis. The solution obtained from the first pass may not be complementary. A second pass is performed pivoting out nonzero variables until a complementary primal feasible solution is obtained. Each pivot in these two passes monotonically decreases the objective function value of the current solution. This guarantees that the point returned by the decomposition is a starting point for phase 2 of the primal algorithm that is described in detail below.
B with xj < 0, a penalty
r is added to the cost cj to
obtain cjr. If the
reduced cost vector, computed with respect to c r
is nonnegative, the penalty r is increased until
either some cj r becomes
negative, or until c r
has negative values for all nonnegative values of the penalty r.
In the former case, the algorithm proceeds, while in the latter case, EKKQSLV
returns control to your program, and declares the problem to be primal infeasible.a = minimum{ -( x k / z
k ) | z k < 0, where k is not a
member of B}
The value a is exactly the same as would be computed
in the ratio test for linear programming.
- (c + Qx) T z
b
= _____________
z TQz
which is the length of the step along the direction z to the
optimizer of the quadratic function on the half-line:
{ x
+ lz | l
0 }.
x + az
is computed.
Furthermore, the basis index set is updated to { B U {j}
}\{k} , and a new basic
solution is computed.
is nonnegative, then
x and the iteration is complete. Processing continues with
step 2.
Otherwise, EKKQSLV sets z = -
x and performs the ratio test from step 8.1 above. An index k
that achieves the ratio a is chosen, and the solution
x x +
az is computed. The basis index
set is updated to B\{k} and a new basic solution
is computed. This step is then repeated
until is nonnegative. This is guaranteed
to occur.
There are exceptions to the rules described above. In the initial phase of the algorithm, before a feasible solution to the primal problem is obtained, the ratio test for a is replaced with a search along a piecewise linear cost function representing both original costs c and the penalties r incurred by violating the nonnegativities.
|
Note: |
Having performed the pivot, the user exit subroutine EKKITRU is called. At this point, you may request that EKKQSLV return to your program. |
The basis inverse is represented by an LU factorization of a basis together
with product form updates. This is done by a sparse factorization algorithm.
(See Suhl.)
This representation of the inverse may not be as well suited to certain quadratic programming problems as other factorizations.
A parametric algorithm is implemented in EKKQPAR that uses the primal algorithm as a subroutine. The parametric algorithm is used to find solutions to the family of problems, parameterized by l:
minimize cTx + ldT x + (1/2) xTQ x
subject to:
Ax = b + le
x 0,
l
0.
By an appropriate choice of the parametric adjustment vectors d and e, sensitivity analysis can be performed. In particular, if d = 0, then the right-hand side is parametrically adjusted, and if e=0, the linear cost is parametrically adjusted. This includes finding the solutions to the parameterized family of quadratic programming problems:
minimize dTx + xTQx /(2l)
which is equivalent to:
minimize ( ldT x + (1/2) xT Qx ) / l
subject to:
Ax = b
x
0
One common use of parametric programming is in portfolio analysis. If the quadratic problem models a portfolio analysis problem, then d is the negative of the expected return vector and Q is the empirical covariance matrix of the portfolio instruments. A reflects the budget constraint, diversity, and quality constraints, as well as any other linear constraints on the portfolio composition. As the parameter 1/l changes from 0 through positive values, the optimization problem reflects increasing sensitivity to risk. The values of these solutions plotted against the value of the parameter 1/l is called the efficient frontier.
This section lists the control variables related to quadratic programming.
For complete information on all the integer and real control variables,
refer to Appendix C. "Control Variables".
The contents of arrays pointed to by index control variables may change during
execution. For information about these control variables, refer to "EKKNGET
- Request Current Start Indices of OSL Information".
|
Note: |
maxint refers to the maximum allowable integer value on your platform, and maxreal refers to the maximum allowable real value on your platform. |
Description: The log frequency.
Description: The current number of iterations that have been performed
in a
solver subroutine.
Description: The maximum number of iterations that will be performed.
Description: The number of the current EKKQPAR parametric adjustment.
Description: The maximum number of parametric adjustments that will
be performed by EKKQPAR.
Description: The problem status.
Description: The maximum number of decomposition iterations.
Description:Row ordering method indicator for interior point algorithm.
Description: The value of the objective function.
Description: The value of the EKKQPAR parameter &lambda..
Description: The value of the EKKQSLV decomposition cutoff.
Footnotes:
(1) The method used is essentially that described in the paper by Forrest and Tomlin. L and U are formed such that U is upper triangular and L U = AB. The updates are done as described in this paper.
(2) Rcholtinytol replaced what was Rcholreltol in OSL Version 1 Release 2. The interior-point algorithm has been changed to remove the Cholesky relative tolerance.
[ Top of Page | Previous Page | Next Page | Table of Contents ]